中国省域经济增长源泉研究:要素和全要素生产率——基于改进空间的随机前沿模型

(辽宁师范大学 海洋经济与可持续发展中心,辽宁 大连 116000)

1　引言

改革开放以来,我国经济发展取得了前所未有的成就,但对我国经济增长的动力却存在很大争议。Krugman[1]指出,我国经济增长主要依靠生产要素投入驱动,全要素生产率(TFP)没有贡献,因此经济增长是不可持续的;董敏杰等[2]的研究显示,自改革开放到20世纪初，TFP对我国经济增长的贡献率达到30%左右。为了具体研究我国经济增长的奇迹,必须回答三个问题:①不同地区的经济增长源泉有何不同？②地区增长之间有何种相互作用？③各地区全要素生产率有何差异？这些问题都要求模型既能计算全要素生产率,又能考虑到各地区之间的相互作用和各自的生产前沿。

吴诣民、张凌翔[3]、李国璋[4]等使用随机前沿模型对我国区域要素回报和全要素生产率的分析表明,全要素生产率是造成地区差异的主要原因,人力资本对西部地区发展有着不可忽视的阻碍作用,但该方法忽视了各地区生产前沿的差异性,导致全要素生产率测度误差偏大。如对落后地区,因为高估了它们的生产前沿,低估了TFP[5],分地区测度会忽视地区间的溢出效应。众多学者采用非参数方法研究全要素生产率,如严鹏飞、王兵[5]、杨文举等[7]对我国不同时期的全要素生产率展开了定量研究,做出了卓有成效的贡献。李兰冰等[8]在此基础上将资源和环境因素纳入测算框架,并将总体绩效向要素绩效延伸,得出劳动生产率、资本生产率、生态要素生产率增速全面放缓的结论。但由于非参数方法的局限性,没有考虑要素投入和随机因素对增长的作用,而随机因素对我国经济增长的影响不能忽略[8],因此这些结论的说服力有所下降。

由于当前的研究不足,本文对现有文献进行了拓展:①将已有的截面数据GWR模型拓展到面板数据的GWR模型,改进后的空间随机前沿模型将面板数据的地理加权回归模型、空间误差模型、随机前沿模型三者结合起来,并给出新模型的计算方法;②将生产前沿、地理相关性和全要素生产率纳入同一框架中考虑,在此基础上计算出各要素和全要素生产率对我国各省域经济增长的贡献率,揭示我国经济增长的要素源泉、时空规律和分布特征。

2　研究方法

2.1　模型设定

改进后的空间随机前沿模型描述为:

yi=β0(i)+Xiβ(i)+vi-ui

(1)

vt=ρWvt+ηt

(2)

式中,yi=[yi1,yi2,…,yiT]′表示第i个生产单位在1到T时段的T×1维产出(取对数);Xi表示第i个生产单位在1到T时段的T×K维投入(取对数)矩阵,i=1,2,3,…,N;β0(i)表示第i个生产单位的截距;β(i)表示待估计的第i个生产单位的K×1维参数向量;ui=[ui1,ui2,…,uiT]′≥0为T×1维技术无效率项向量,代表第i个生产单位1到T时段的技术无效率程度;vi=[vi1,vi2,…,viT]′为T×1维的双边误差项向量,表示不可控的经济系统外部影响因素和数据测度误差等;ηt=[ηit,η3t,…,ηNt]′为N×1维的随机干扰向量。

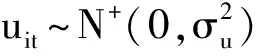
(3)

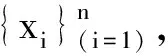
(4)

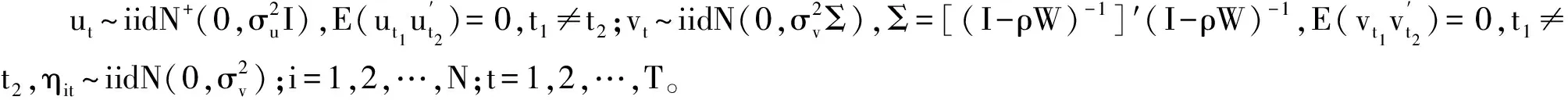
(5)

其中:

εt=vt-ut

(6)

(7)

(8)

Φ(·)是多元标准正态分布函数:

(9)

基于此,可得模型的对数似然函数:

(10)

如果εit已知,则可通过最大化似然函数式(10)来解得参数σu,σv,ρ。

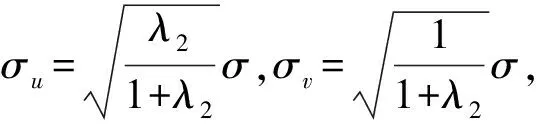
(11)

ei=vi-ui+E(ui),易证E(ei)=E(vi)=0。

可见式(11)即为一个面板数据的地理加权回归模型(vi有自相关性,导致ei也有自相关性,故计算时采用稳健标准差)。地理加权回归(GWR)[10]扩展了传统的回归框架,允许局部而不是全局的参数估计,该模型应对研究区域内的每一点i,指定相应的一组权wij。传统的GWR模型只适用于截面数据,本文将其拓展之后也适用于面板数据(计算过程可向作者索要)。

给定研究区域内的一点i,其权重定义为:

(12)

式中,d(i,j)为i,j两点之间的距离;θ>0为窗宽或光滑参数;θ的大小决定了拟合曲面的光滑性。在给定θ时,i,j两点之间的距离越大,权重就越小。光滑参数θ一般用交叉证实法[10]确定,即令:

(13)

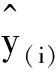
CV(θ0)=minCV(θ)

(14)

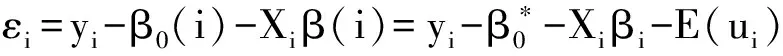
(15)

式中,yit表示i地区t时期的产出;Xit表示投入要素向量;A为线性函数中的常数项,定义全要素生产率为:

TFPit=exp(A-uit)

(16)

基于上式,对某地区的产出增长可分解为要素贡献和全要素生产率差异两部分。

2.2　Solow增长核算法

根据本文的思路,参考Brock[11]、Xepapadeas[12]的C-D生产函数设定形式,将TFP看作投入要素,则有:

Y=F(KG,KF,L,Z,T,P)

(17)

式中,KG为国内资本存量;KF为FDI存量;L为劳动力投入;Z为环境消耗;T为技术进步；P为全要素生产率。对上式的时间求导,并做相应的处理,可得:

(18)

上式右端即为各部分对经济增长的贡献率。

3　指标选取

本文涉及2000—2014年的产出、国内资本存量、FDI存量、劳动投入、环境消耗和技术进步6个指标的省际面板数据(未包括香港特别行政区、澳门特别行政区、台湾地区和西藏自治区,下同)。其来源为:①产出。以2000年为基期的实际地区生产总值,数据来源于相关年份的《中国统计年鉴》。②资本存量、FDI存量。Borensztein等[13]的研究表明,FDI与国内投资对经济增长的影响弹性存在显著差异,因此有必要将国外资本与国内资本分离。国内资本存量采用总的资本存量减去FDI存量得到,总的资本存量采用永续盘存法[14]估算。其中,单豪杰并未估算重庆的资本存量,参考孙辉等[15]估算的数据计算出重庆和四川的资本存量之比,并基于此对采用单豪杰方法估算出重庆与四川资本存量之和进行比例分配,总资本存量以2000年为基期。③劳动力投入。在劳动投入对经济增长的贡献分析中,投入数据不仅取决于劳动要素的投入量,还与劳动要素质量、劳动使用时间等因素有关。我国市场机制不够完善,劳动报酬不能合理地反应出劳动投入。因此,与多数国内文献一样,采用劳动者人数取代劳动投入,数据来源于各地区相关年份的统计年鉴。④环境消耗。部分学者认为,环境消耗对我国经济增长贡献不可忽视,如刘瑞翔[16]测算出环境消耗对经济增长的贡献率为9.25%,因此有必要将环境消耗纳入测算框架。本文将污水(亿t)排放量、废气(亿t)排放量之和作为环境消耗指标,数据来源于相关年份的《中国能源统计年鉴》和《中国统计年鉴》。⑤技术进步。由于我国的法制系统并不健全,专利能否有效地转化为技术进步、推动经济增长问题一直备受争议。但自2001年我国加入世界贸易组织以来,我国随之采用了“与贸易有关的知识产权协定”(TRIPs),并将国内的知识产权保护系统与国际进行接轨,我国的专利数量也在2000年之后大幅增加,因此本文采用专利数作为指标衡量技术进步。

4　计算结果与实证分析

4.1　空间相关性检验

为了考察数据是否存在空间依赖性,首先以各省GDP数据计算Moran′s I[17],考虑到GDP数据未必服从渐近的正态分布,因此以本文上述变量作为协变量,对GDP数据进行回归后,使用标准化处理后的残差项和行标准化的权重矩阵进行全局莫兰指数检验,计算结果见表1。

表1　莫兰指数I

从表1可见，所有年份的莫兰指数均大于0且通过了5%显著性水平检验,GDP水平显示出强烈的空间正相关,说明高水平省份倾向于与其他高水平省份临近,低水平省份同样在空间上集聚,需要在模型中考虑地理相关性。从动态演进看,莫兰指数有轻微的波动下降现象,说明省域GDP在空间集聚上有弱化趋势。

全局莫兰指数反映了空间变量的整体空间相关状况,但可能忽略局部地区的非典型性特征[17],因此还需进行局域空间相关性分析。我国30个省域2002年、2006年、2010年、2014年在LISA空间集聚(图1),且均通过了5%显著性水平检验。

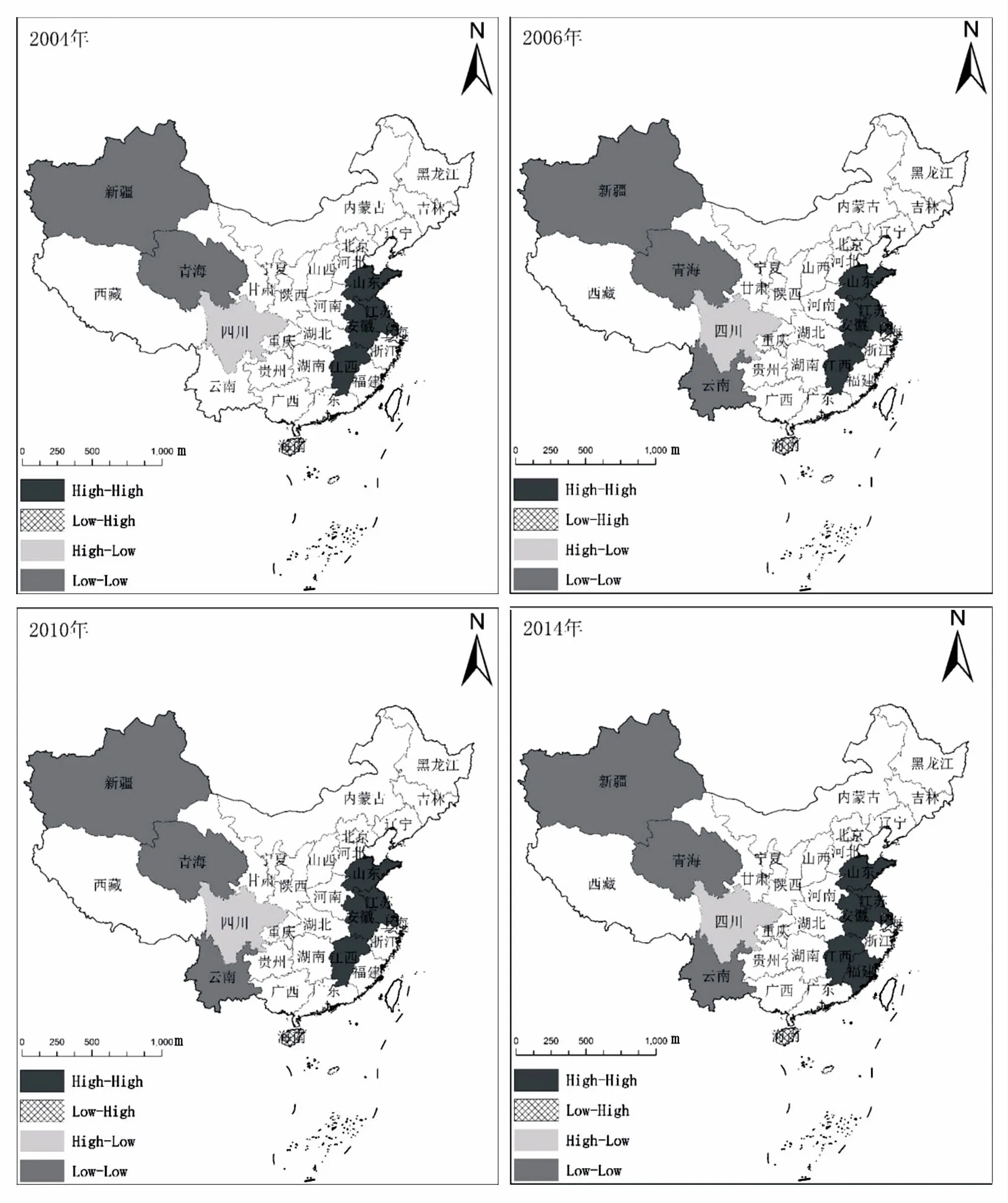
图1　局域空间自相关LISA集群图

由图1可见,山东、江苏、安徽等东部沿海地区处于高—高(H-H)型集聚区,新疆、青海、云南等西部地区分布于低—低(L-L)型集聚区;四川经济发展优于周边地区,分布于高—低(H-L)型集聚区;海南落后于相邻的广东,分布于低—高(L-H)型集聚区。正负局域相关省份数量和分布稳定,但仍有个别省存在类型迁移:福建由集聚不显著地区迁跃为H-H型集聚区,受益于周边发达地区,福建发展速度提升,统计数据显示自2010年之后福建年均GDP增速达10%以上;云南由集聚不显著地区跃迁为L-L型集聚区,发展速度放缓。

4.2　模型参数估计结果

模型计算结果见表2。模型的拟合优度为0.987、空间误差自回归系数为-12.42,说明扰动项之间存在着显著的空间相关性。本文将国内资本存量缩写为GK(对应数据第一行为模型系数,第二行为贡献率),FDI存量缩写为FDI,劳动力投入缩写为Labor,环境消耗缩写为Env,技术进步缩写为Tec,全要素生产率TFP和各要素贡献率只列出了均值。从计算结果看,模型拟合度达到要求,对单个系数的显著性检验也基本通过。由表2可见,除新疆地区的环境消耗和技术进步外,其他要素投入对经济的增长都有正向作用,而新疆的这两个指标并未通过显著性检验。

表2　要素系数及贡献率

注:1.***、**、*分别表示在5%、10%、20%水平上显著;2.TFP项无显著性检验。

自1979年改革开放至今,我国经济的年均增长率高达9.6%,GDP和国民收入每七到八年就能翻一番。我国经济的高速增长引发了经济学界的争论,但几乎没有学者否认资本投入对我国经济增长的贡献。如Chow、Lin[18]的研究显示,1978—1998年我国GDP的增长有62%归功于资本投资。大部分相关文献表明,我国的全要素生产率增速在20世纪90年代中期开始减缓,如Zheng、Hu[19]估计,1995—2001年我国全要素生产率每年上升0.6%—2.8%,而在1995年之前仅为3.2%—4.5%,此后我国资本投入增速开始显著超过GDP增速,资本对我国经济高速增长的贡献不可忽视。就资本贡献而言,本文结论与主流观念无显著性差异。统计数据显示,2000—2014年我国的资本存量增速高达15%。由表2可知,多数地区资本存量的系数与贡献率均显著超过其他要素,GDP增长主要归功于资本存量增加,国内资本存量贡献比FDI存量贡献份额更大;FDI存量对经济增长的贡献率普遍在20%左右,对我国经济增长已起到了相当大的推动作用。甘肃、青海、新疆等省份地理位置偏远,难以吸引外商投资,FDI贡献率显著偏低。此外,FDI存量弹性在空间上由东到西呈现下降趋势,说明西部地区不仅外商投资少,对外商投资的利用率有待提升;广东等发达沿海地区FDI存量贡献率较低,但FDI存量弹性与多数东南地区没有显著差异,贡献被其他要素所掩盖。有学者认为,外商投资能带来以劳动者为载体的软技术流入,推动经济发展。如Cheung、Lin[20]的研究表明,外商直接投资较多的省份收到的专利申请数目也较大,本文也有类似的结果:FDI存量贡献率超过20%的地区,多数为发达或高速发展中的地区,如北京、浙江、重庆等地。

在20世纪末,为了缓解国有企业效率低下的问题,创造了更为市场化的工资薪酬结构。我国进行了三次工资改革,国有企业大规模裁员,劳动力市场从集中管制走向市场,企业工资预算与企业效益挂钩。劳动力市场的改革和人口红利为我国经济的增长做出了巨大贡献。例如，Wang、Yao[21]的研究发现,1978—1999年劳动力可解释我国经济增长的16%;Arayama、Miyoshi[22]也认为,人力资本可解释我国15%的GDP增长。但步入21世纪后,情况有所改变。生产要素的再分配具有局限性,不管是更高效地利用资本还是更高效地利用劳动力,都不能维持经济长期增长。从表2可见,步入新世纪后我国各省劳动投入的贡献率普遍不大,我国的劳动力参与率一直很高,并且长期的计划生育政策拉低了人口增长速度,所以劳动力投入的增加对经济增长的贡献有限。此外,我国劳动力就业结构性矛盾依然突出,人才结构失衡,供求矛盾巨大。广西、河南、重庆、四川、贵州、陕西等省市的劳动力贡献较低,这些地区或地理位置偏远、交通不便,或发展落后、劳动力流失。其中,贵州、云南两地由于劳动力投入出现负增长,劳动力贡献率为负;劳动力投入系数由东到西呈现上升的趋势,表明西部内陆地区劳动力投入的边际收益更高,进一步验证了劳动力由西向东迁移的观点。

2003—2013年我国废水排放量年均复合增长率达到4.22%,废气年排放量大体不变,约为388169亿m3,排放量巨大。刘瑞祥[15]认为,21世纪后环境消耗对我国经济增长的贡献率达9.25%,本文的计算结果多数地区与该数据相近,北京、天津、河北、山西等地更是达到20%左右,表明资源环境为我国经济高速增长付出了巨大代价。20世纪末期,重化工业特征和化石能源占比过高问题再次凸显,协调结构和集约型经济增长模式有待推进。近几年日益严重的雾霾问题佐证了这一点。新疆、青海、海南等地环境消耗贡献率较低,且相关系数未通过显著性检验,说明这些地区在发展过程中并未过度消耗自然资源。

学界普遍认为,创新所带来的技术进步是一个国家长期经济增长潜力的重要影响因素。作为高校和各种高科技企业集中地的北京,技术进步对经济增长的贡献率最高,其余地区相对较低,主要原因是这些地区技术转化为生产率需要的时间过长,在技术能创造财富之前,持续性的投入使其贡献率低下[23];另一个原因是提高普通劳动者的知识和技能水平,才能使新技术转化为生产力[7]。此外,技术进步系数也普遍较低,且相当一部分地区技术进步系数不显著,如河北、山西、内蒙、云南、山西、青海等内陆或落后省份,不但再次说明技术进步对这些地区经济增长的推动作用有限,而且能推断我国多数地区的技术进步可能并非来自内生的技术创新,而是来自对外来技术的模仿。

从图1可见,我国30个省份2002年、2006年、2010年、2014年全要素生产率变化的地理空间上的四分位图,使用自然断点法将全要素生产率从低到高分为四个等级,全要素生产率的平均贡献率见图2。从图2可见,部分省份的全要素生产率在空间上是集聚的。即高全要素生产率和高全要素生产率地区,低全要素生产率和低全要素生产率的地区在空间上呈现相邻或集聚特性,且随着时间的推进,俱乐部趋从现象越发显著,而不同俱乐部之间差距持续扩大。此外,许多地区全要素生产率有着由低到高再降低的趋势,提高的原因在于21世纪初全球科技进步和信息化革命带来的整体技术水平上升,而下降则是因为随着市场化和国际化程度的提高,要素在不同领域转移产生的边际报酬递减。全要素生产率的提升为经济增长带来的贡献各省份相差较大,除黑龙江、吉林、天津、山东、江苏、广东等东部地区较高外,四川等中部地区也较高。李胜文、李大胜[5]等研究表明,中部效率并不比东部低,而全要素生产率的变化是由技术效率变化决定的,与本文结果无显著差异。作为发达地区的北京等地全要素生产率贡献率并不高,甚至为负值,这些地区有着长期大量的要素投入,使经济运行时的效率有所下降,刘亚军[25]等对浙江的研究有着近似的结果。

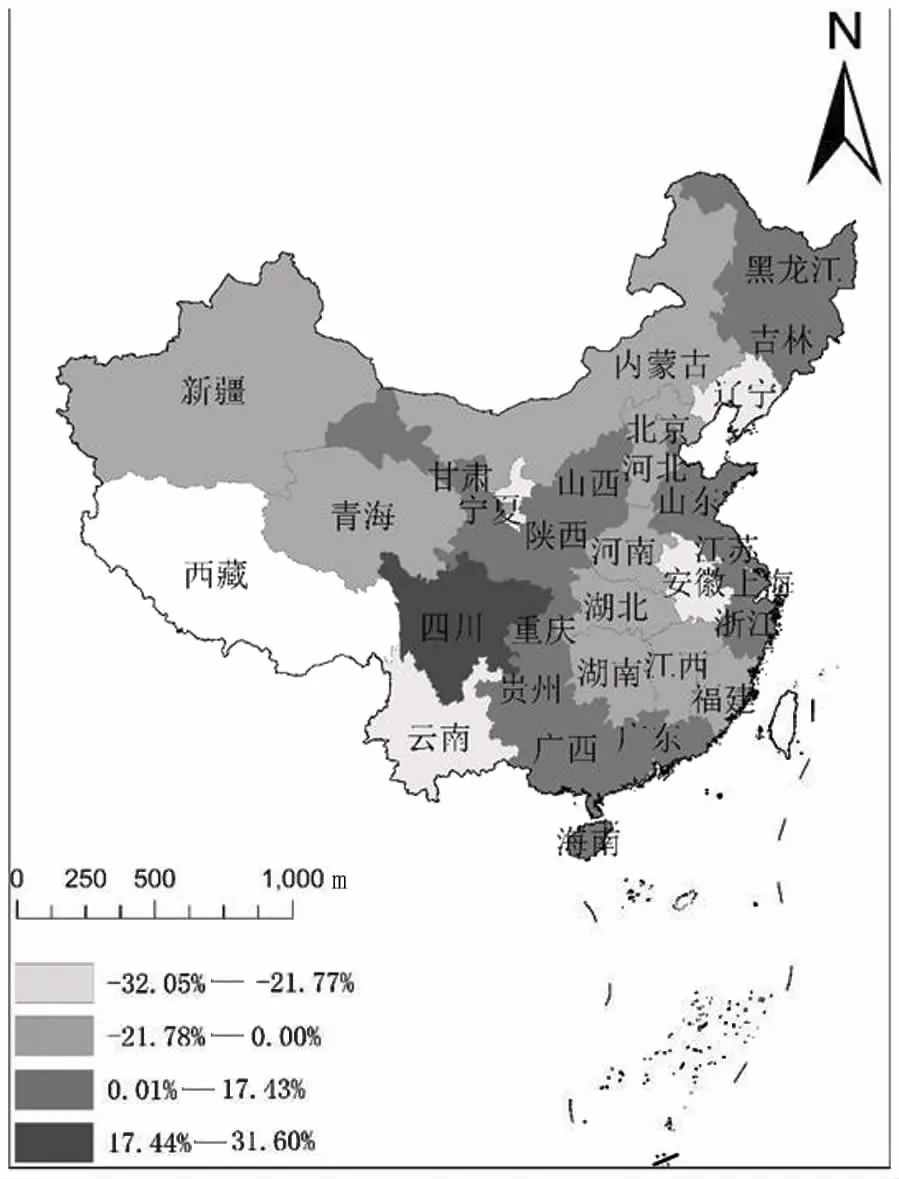
图2　全要素生产率贡献率分布

5　结论与政策含义

本文提出了一个基于改进的随机前沿生产函数的地区增长分析框架,创建性地将空间相关性纳入其中,从空间和动态视角测算了各要素和全要素生产率在我国地区经济增长中的贡献。研究发现:①步入新世纪后,资本投入仍是我国经济增长的主要源泉,尤其是部分落后地区更依赖资本投入。国外投资的重要性日益突显,在东部、东南部等对外交流频繁地区,外商投资对经济增长的贡献已仅次于国内资本的贡献。②劳动力投入对各省经济增长的贡献远低于资本存量的贡献,同时东部劳动力投入弹性低于中西部,意味着中部和西部劳动力流失现象显著,而东部劳动力投入超过了帕累托最优,经济运行处于不均衡状态。③多数地区经济增长对环境资源依赖程度较大,环境消耗已是我国经济增长的主要因素之一。海南、青海、广西等少数地区或是以旅游业为主,或是地处偏僻人烟稀少,环境消耗对经济增长的贡献率较低。④技术进步的贡献率普遍较低,说明我国对新技术的开发利用程度仍不够;相当多的地区技术进步系数不显著,这类地区主要集中在西部、北部地区,如云南、陕西、新疆、内蒙、吉林等,反映出这些地区的技术较落后。⑤中部地区全要素生产率与贡献率并不比东部低,原因是本文考虑了各地区生产前沿的差异。各省份全要素生产率的贡献率差异巨大,同一俱乐部内收敛趋势显著,然而不同俱乐部之间差距持续扩大,表明我国地区间存在较强的技术壁垒,只有少数发达地区从技术进步和全要素生产率改善中受益较大;近年来全要素生产率来整体呈下降趋势,表明多数地区存在着要素投入比例不均衡、部分要素边际产出下降。

上述研究结论可引申以下政策含义:①西部地区加快完善基础设施建设,招商引资,进一步增加资本供给,并提高投资效率,是今后缩小与东部地区差异的有效途径;东部地区则需要在保持自身优势的同时寻找新的经济增长点,改善投资扭曲引起的资本配置结构性障碍。②中西部地区需要完善人才引进策略,增加高端人力资源累积,同时提升劳动者知识技能水平,提高对新工艺、新方法的吸收和适应能力,加强就业政策制定、就业环境创造;东部地区则需进一步扩大人力资本在经济增长中的作用,改善就业结构配置,增加人力资本收益。③京津冀、长三角等东部和东南沿海地区需要限制污染排放,加强环境治理。山西等煤和矿石产地则需按计划、有限度地开采,积极寻找经济转型方向,实现可持续发展。为了推动经济增长,部分地区可能会默许环境标准降低。此外,环境污染具有外部性,即使当地政府严格管制也很难降低环境污染带来的危害。因此,只有我国各地积极合作,才能从根本上控制污染。④我国各地区应鼓励技术创新,提升人力资本水平,加快人力资本在地区间的流动,有利于加速技术模仿、追赶和扩散,推动技术进步转化为生产力。⑤中部地区可通过增加研发投入、引进先进技术等手段,提高技术水平;东部可凭借充裕的资金优势,在提高自主创新活跃度的同时,强调利用新技术溢出效应加快先进技术的扩散,以便在提高生产力的同时能保持全要素生产率具有较高的水平,避免过多要素投入产生的资源浪费;西部则需要双管齐下,提高管理和技术水平。政府应对地区发展进行调节,尤其要促进地区间技术扩散,使各地区更好地分享技术创新和体制创新的成果。