钢筋超高性能混凝土梁抗剪性能试验研究

陈宝春, 吴前文, 黄卿维, 马熙伦, 苏家战

(福州大学土木工程学院, 福建 福州　350116)

0　引言

超高性能混凝土(ultra-high performance concrete, UHPC)是一种具有超高抗压、 抗拉强度、 高韧性和高耐久性的新型水泥基复合材料, 它包含活性粉末混凝土(RPC)、 超高性能纤维增强混凝土(UHPFRC)等[1-2].将UHPC用于梁构件中能够提高构件的承载能力、 减小尺寸和减少钢筋的用量.抗剪承载力是结构受力的重要内容, 文献[3-5]对UHPC梁受剪性能进行试验研究, 其截面型式有矩形、 T形和I形等, 试验参数有剪跨比、 箍筋率、 纵筋率和纤维掺量等.UHPC作为一种新型材料, 其材料组份与特性有别于普通混凝土, 使得UHPC梁的受剪破坏机理也有别于普通混凝土梁.尽管国内外学者对UHPC梁的抗剪性能已开展一定的研究, 但由于UHPC抗剪机理的复杂性, 对UHPC梁的抗剪破坏形态、 极限承载力等方面还未有一致的结论.文献[6]基于桁架-拱模型, 通过UHPC梁的抗剪机理分析, 提出考虑UHPC的抗拉作用的抗剪承载力计算公式, 计算结果与收集到UHPC梁的抗剪试验结果吻合较好, 但该文未进行试验研究.本研究在文献[6]的基础上考虑钢纤维掺量、 剪跨比、 箍筋配箍率、 纵筋配筋率4个影响因素, 制作11根试验梁进行UHPC梁的抗剪性能试验研究.通过试验研究, 进一步揭示UHPC梁的抗剪破坏机理, 并对文献[6]提出的UHPC抗剪承载力计算公式进行进一步的论证与修正.

1　试验概况

1.1　试验梁

图1　部分梁截面尺寸及配筋(单位： mm)　Fig.1　Sectional dimension and reinforcement of beams (unit: mm)

本试验共设计了11根矩形截面梁, 各试验梁的截面尺寸相同, 部分梁截面尺寸与配筋如图1所示.梁长1 200 mm, 计算跨度1 000 mm.试验梁的主要变化参数为： 钢纤维体积掺量Vf、 剪跨比λ、 箍筋配箍率ρsv及纵筋配筋率ρs.试验梁参数详见表1.其中L5无箍筋, L6和L7箍筋间距分别为100 mm和150 mm, 其余梁箍筋间距均为200 mm； L8下部为2根直径25 mm和2根直径22 mm的钢筋, L9下部采用4根直径22 mm的钢筋, L1～L7和L10～L11的下部纵筋均采用4根直径25 mm的钢筋.本文的荷载值为千斤顶所施加的荷载值F, 而受剪承载力V=F/2.

表1　试验梁参数

1.2　试验装置与测量方案

试验通过2 000 kN千斤顶与荷载分配梁系统对试验梁进行四分点加载, 加载装置照片如图2所示.

图2　试件加载装置与测点布置图(单位： mm)Fig.2　Test setup and measuring point layout(unit： mm)

试验梁在跨中和两个加载点位置处布置3个位移测点进行挠度测试, 在剪跨区的纵筋、 箍筋和UHPC分别布置应变片进行纵向应变和剪应变的测试, 具体测试截面与测点布置见图2.其中, 采用裂缝测宽仪进行UHPC梁裂缝宽度的测试.

1.3　材料性能

UHPC的配合比： 水胶比为0.18, 水泥∶硅灰∶细砂∶减水剂=1∶0.3∶1.2∶0.025, 钢纤维体积率分别为0%、 1%、 2%、 3%.试块与试验梁同批浇筑且在同条件下进行养护.UHPC试块尺寸采用100 mm× 100 mm×100 mm、 100 mm×100 mm×300 mm分别测得UHPC立方体抗压强度fc与弹性模量Ec, 单轴拉伸强度ft采用有效尺寸为50 mm×100 mm×150 mm的哑铃型试件.UHPC和钢筋力学性能测定结果分别如表2和表3所示.

表2　UHPC力学性能

表3　钢筋材性力学性能

2　试验结果及分析

2.1　基本情况

图3给出UHPC梁加载点的荷载-挠度曲线.其中UHPC梁的极限荷载是指荷载不能再继续增加而梁挠度急剧下降时对应的荷载值.从图中可见, UHPC梁的试验过程分为弹性阶段、 裂缝开展阶段和屈服阶段.

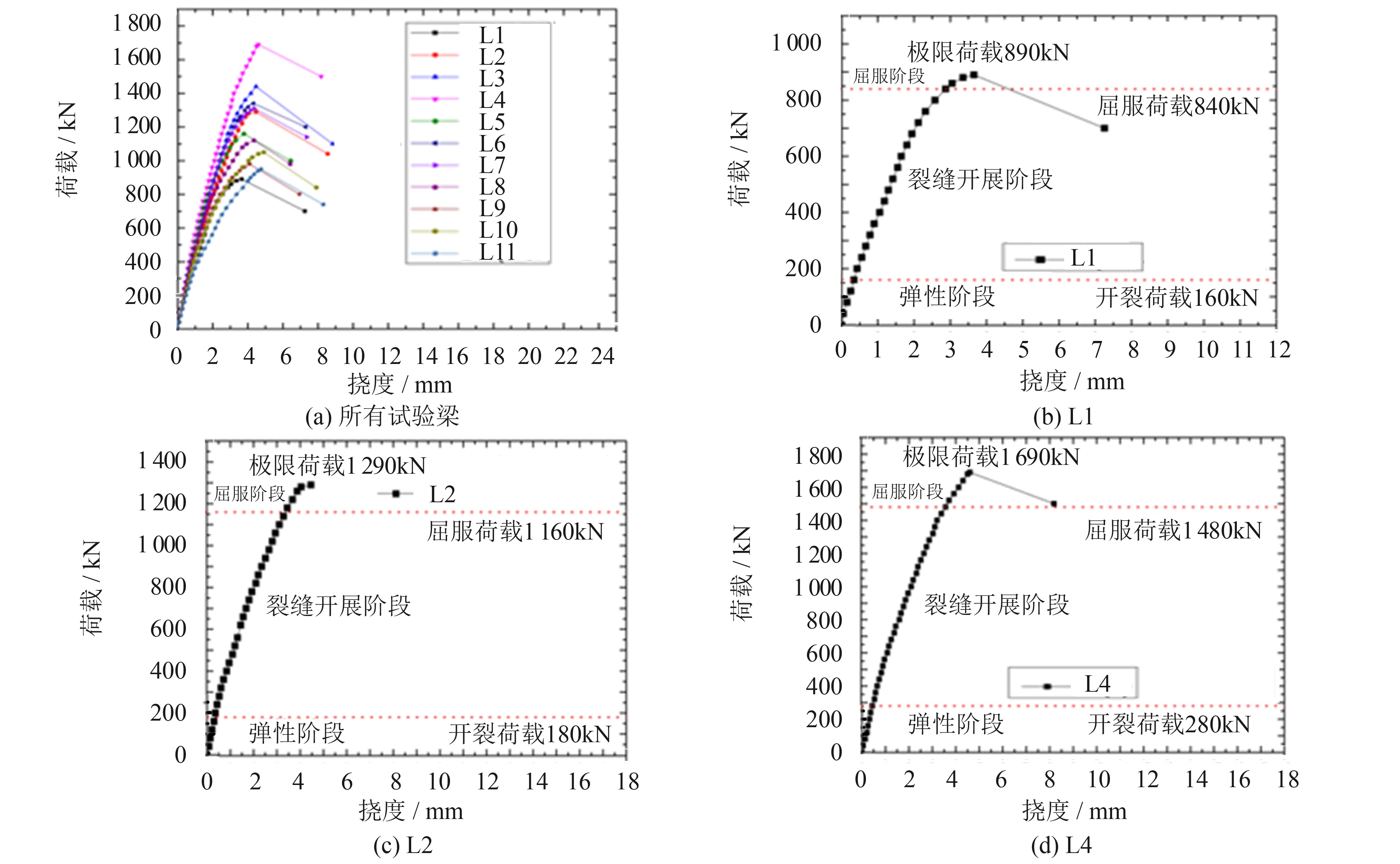
图3　UHPC梁加载点荷载-挠度曲线Fig.3　Load-deflection curve at the loading point

图4　部分试验梁裂缝分布图Fig.4　Crack distribution of some test beams

图4给出部分试验梁裂缝分布图.从图中可以看出, 由于试验参数的不同, 梁的破坏形态并不完全相同, 其中L1梁为斜压破坏, L3、 L4梁发生了超筋弯曲破坏, 其余试验梁均发生了剪压破坏.L1梁试验中, 荷载加载至160 kN (18%F)时, 在纯弯区底部出现首条竖向裂缝, 裂缝宽度为0.06 mm； 荷载达到200 kN时, 梁腹部支座与加载点之间出现了斜裂缝, 随着荷载的增加, 剪跨区出现一些几乎平行的斜裂缝.而后, 支座与加载点处的裂缝从试验梁腹部分别向加载点与支座处延伸.而纯弯区的裂缝发展缓慢甚至停止发展.当荷载加载至840 kN (94%F)时, 梁进入屈服阶段, 梁腹部混凝土被分割若干个条状体, 当荷载加载至890 kN时, 条状体的混凝土被压碎且挠度急剧下降, 试验中止, 中止时试验梁主裂缝宽度为4.64 mm.该梁在破坏时呈现出明显的脆性, 在工程设计中应避免这种破坏形式.

L2、 L5～L11等8根梁均属于剪压破坏, 这些梁所对应的极限承载力是本文要考察的抗剪极限承载力.以L2为例, 当荷载加载至180 kN (14%F)时, 在梁剪跨区底部出现首条弯曲裂缝, 裂缝宽度为0.04 mm； 随着荷载的增加到220 kN时, 在剪跨区腹部出现首条斜裂缝, 随着荷载的增加支座与加载点处的斜裂缝裂缝从试验梁腹部分别向加载点与支座处延伸.当荷载加载至1 160 kN (90%F)时, 梁进入屈服阶段, 密集的斜裂缝形成一条裂缝宽度明显的临界斜裂缝, 当荷载加载至1 290 kN时, 与临界斜裂缝相交的箍筋发生屈服后, 临界斜裂缝附近的混凝土被压碎, 随后试验中止, 中止时试验梁主裂缝宽度为2.14 mm.

L3和L4两根梁出现超筋弯曲破坏.以L4为例, 当荷载加载至280 kN (17%F)时, 在梁腹板底部加载点处出现了首条弯曲裂缝, 裂缝宽度为0.06 mm； 当荷载加载至1 480 kN (88%F)时, 梁进入屈服阶段, 在试验梁顶部两个加载点之间的混凝土被压碎形成塑性铰, 当荷载加载至1 690 kN时, 压碎区由梁顶向梁底发展, 挠度急速下降, 试验中止, 中止时试验梁剪跨区斜裂缝的最大宽度为1.64 mm.

2.3　试验参数分析

图5给出不同参数下的荷载-加载点处挠度曲线.

图5　不同参数下的荷载-加载点处挠度曲线Fig.5　Load-deflection curve at the loading point under different parameters

1) 钢纤维掺量.从图5(a)可看出, 由于钢纤维掺量的增加使得UHPC的受压弹性模量增加, 从而提高了试验梁的弯曲刚度和变形能力.L1～L4受剪极限承载力分别为445、 645、 720、 845 kN.对于发生受剪破坏的L1、 L2, 当钢纤维掺量从0%增加到1%时试验梁的受剪极限承载力增加了44.9%.L3、 L4发生弯曲破坏, 这说明钢纤维掺量对梁的受剪承载力的影响大于受弯承载力.梁开裂前由于钢纤维与UHPC细骨料之间的咬合作用, 使得UHPC的抗裂能力增强(见表1).在实际工程中, 虽然增加钢纤维掺量可提高梁的抗剪承载力, 但不应掺入过多的钢纤维以防止超筋破坏.

2) 配箍率.从图5(b)可看出, 配箍率的增加并不能提高梁的刚度, 但可提高试验梁极限承载力和极限挠度.L5、 L2、 L6、 L7受剪承载力分别为580、 645、 655、 670 kN.与不配箍筋的L5相比, 配箍筋的L2的极限受剪承载力明显提高, 但增加配箍率对梁极限承载力提高不明显.

3) 纵筋率.从图5(c)可看出, L9、 L8、 L2受剪承载力分别为490、 560、 645 kN.试验梁的开裂荷载和极限荷载均随着纵筋率的增大而增大, 这是由于钢纤维的存在增强了纵筋的销栓作用.

4) 剪跨比.从图5(d)可看出, 当梁进入裂缝开展阶段后, 挠度随着剪跨比的增加而增加.L2、 L10、 L11受剪承载力分别为645、 525、 475 kN, 试验梁的受剪承载力随着剪跨比的增大而减小.在普通混凝土梁中认为当剪跨比λ<1.5时, 剪跨比对梁受剪承载力无影响, 当1<λ<3时普通混凝土梁发生剪压破坏.而在UHPC梁中当剪跨比λ<1.5时, 剪跨比增加对试验梁承载力仍有明显的影响, 钢纤维掺量为0%的L1(λ=1.2)发生斜压破坏, 说明影响UHPC梁受剪破坏形态的剪跨比范围可能与普通混凝土梁不同.

3　UHPC梁抗剪承载力计算方法

图6　试验梁破坏形式Fig.6　Failure mode of beam

对UHPC梁抗剪公式的推导是根据普通混凝土梁的抗剪理论而来, 但由于忽略了UHPC本身的抗拉强度, 导致计算结果离散性较大低估了UHPC梁的受剪承载力, 无法为工程设计提供参考.文献[6]基于桁架-拱模型, 通过UHPC梁的受剪机理分析, 提出考虑UHPC的抗拉作用的受剪承载力计算公式, 计算结果与收集到的UHPC梁的受剪试验结果吻合较好.本试验中, 发现模型梁的破坏模式符合桁架-拱模型, 如图6所示.故本文选择文献[6]的受剪承载力计算公式为基本公式, 根据本文试验结果进行进一步改进.由文献[6]可知：

桁架模型承担的剪力：

Vtr=(ρsvfyv+σt)bwzcotθ

(1)

桁架模型中斜压杆的压应力：

σc=(ρsvfyv+σt)(1+cot2θ)

(2)

UHPC富余强度：

σa=vfc-cos(θ-φ)σc

(3)

拱模型承担的剪力：

Vac=σabwh0cos2θtanφ

(4)

UHPC的抗剪承载力：

V=Vtr+Vac

(5)

图7　抗剪承载力计算值与试验值对比Fig.7　Comparison between test result and calculated result

将试验中发生剪压破坏的试验梁、 文献[6～8]共74根UHPC梁的试验值与通过文献[6]计算得到的计算值进行对比分析(见图7), 计算值与实验值比值的平均值为0.96, 标准差为0.16.

根据试验结果, 对文献[6]提出的公式进行如下的改进：

1) 从上节的分析可知纵筋率对UHPC梁受剪承载力有影响, 根据文献[9]将桁架模型中斜裂缝区域内梁横截面混凝土的实际有效受压区截面积取为Ae=ηbwz, 将其影响考虑到式(2)中, 则有：

桁架模型中斜压杆的压应力：

(6)

其中:η为考虑纵筋对UHPC的约束作用, 根据文献[9],η=0.89, 本文为方便计算取η=0.9.根据文献[6]取θ=45°, cos(θ-φ)=0.9.

将式(6)代入式(3)中求得σa后, 将σa代入式(4), 最后求得UHPC的受剪承载力为：

(7)

2) 在荷载作用下, 梁腹部UHPC处于二轴拉、 压应力状态, 同普通混凝土一样会发生软化现象, 使得复合应力状态下的UHPC抗压强度降低, 一般通过软化系数v来考虑UHPC的强度降低.软化系数v一般是通过收集试验值进行拟合.文献[6]收集了51根梁, 拟合得到UHPC的软化系数取0.7.本文收集共74根梁进行拟合得到UHPC的软化系数取v=0.65.

图8　修正后的抗剪承载力计算值与试验值对比Fig.8　　　　Comparison between test result and calculated result by proposed method

3) 文献[6]中剪跨比的取值范围是根据普通混凝土来取的, 而在普通混凝土梁中剪跨比的范围为1.5≤λ≤3, 对于本文中的8根发生剪压破坏且剪跨比λ=1.2与λ=1.4的试验梁, 采用文献[6]计算的计算值会小于试验值.故本文对式(7)中的λ的适用范围进行调整： 对UHPC梁受剪承载力公式中剪跨比的范围取为1.2≤λ≤3, 当λ>3时, 取λ=3; 当λ<1.2时, 取λ=1.2.

对修正后的式(7)进行验证, 验证结果见图8.计算值与实验值比值的平均值为0.99, 标准差为0.13.相对于文献[6]的计算方法, 本文的UHPC梁受剪承载力计算方法的准确性与适用性进一步提高, 可为UHPC梁的工程设计提供参考.

4　结语

1) UHPC梁的受剪承载能力随着钢纤维掺量、 纵筋配筋率、 配箍率的增加而提高, 随着剪跨比的增加而降低.对梁受剪承载力影响最大的是钢纤维掺量, 其次为剪跨比、 纵筋率, 最小的是配箍率.

2) 钢纤维掺量的增加明显提高梁的抗弯刚度和变形能力, 钢纤维掺量的变化会导致试验梁破坏形态的变化.

3) 对目前UHPC梁抗剪计算方法中适用性较好的算法进行修正.按该公式计算得到的计算值与试验值比值的平均值为0.99, 标准差为0.13, 实验值与计算值吻合良好, 可为UHPC梁的工程设计提供参考.