再制造变速箱箱体模态锤击试验的柔性支承设计

黄　杨，向民奇，钱　洵，孙　亮，何　潇，袁大海

（广西大学机械工程学院，广西 南宁 530004）

振动模态是弹性结构固有的、整体的特性。通过对结构进行模态分析可以弄清结构在某一频率范围内各阶模态的特性，由此可以预测结构在此频段内在外部或内部振源激励下产生的实际振动响应。因此，模态分析是结构动态设计及损伤检测的重要方法。模态参数识别的研究中，不同的支撑方式，即自由边界模拟对模态参数提取结果影响较大。黄琴等[1]研究了橡皮绳悬挂、轮胎支撑、海绵支撑三种方式下铝制圆盘模态参数提取结果的差异，结果表明，轮胎支撑下铝制圆盘试验模态参数与有限元数值分析结果最为接近，进一步分析发现，不同轮胎胎压对模态参数的影响也很大。田晶等[2]研究了不同支撑方式、不同支撑位置对钢板模态参数提取结果的影响，试验结果显示，对于质量较小的钢板，采用悬挂的支撑方式模态参数提取结果更准确，而且悬挂点越少，结果越准确。目前，模态参数识别的研究中，对研究对象的支撑方式常采用自由支撑、固定支撑、原装支撑三种。所谓自由支撑实际上是为了减少其他约束条件对试验结果产生的影响，对研究对象进行自由边界条件的模态。由于各种条件的限制，达到完美的自由边界条件几乎不可能，因此，自由边界条件模拟的好坏，在很大程度上决定了试验结果的准确性。

对于质量较大的中大型零部件，常采用弹簧支承模拟其自由边界，因为选用合适的弹簧，不仅可以降低支承装置对零部件的约束，而且可以使零部件具备一定的行程，得到较好的振动响应效果。同时，当系统固有频率小于研究对象第一阶弹性模态频率的五分之一时，柔软支撑对结构模态参数提取结果的影响将会很小[3]。

针对变速箱箱体的再制造加工之前，需要对其进行全面的损伤检测[4]，本文选择利用模态参数识别对其进行损伤检测。由于再制造箱体为拆卸下来的零部件，对其分析不用考虑其工作状态，故可以采用自由支撑。为了准确提取再制造箱体零件的模态参数，设计了锤击实验过程中专用的柔性支承装置，并通过试验验证了所设计装置的有效性。结果表明，柔性支承装置不仅能稳定支承箱体，系统输入输出数据相干性较好，而且满足箱体自由边界模拟的条件，实现了箱体模态频率的准确提取。

1　模态分析理论基础

有限元分析的基本思想是将研究对象离散成一系列由弹簧、阻尼器、节点等构成的单元，这样，原本拥有无数个自由度的系统成了有限个结构单元组成的系统。假设变速箱箱体是理想状态的线性系统，根据Darren Bell原理，振动微分方程（1）可以用来近似描述该系统[5]：

式（1）中，[M]、[C]、[K]分别代表变速箱箱体的质量、阻尼和刚度矩阵，[M]、[C]、[K]都是实对称、阶数为n 的矩阵；{δ}、{δ˙} 、{δ¨} 分别代表变速箱箱体的位移、速度、加速度向量，同样{δ}、{δ˙} 、{δ¨}是阶数为 n 的向量；{P}为变速箱箱体动态激励的阶向量。由于外部动载荷为零且阻尼对系统的影响不大，在求解结构自由振动特性参数时，可以忽略{C}和{P}.从而，系统振动微分方程可表达为：

设方程（2）的特解为：

式中{Φ}为自由振动的幅值向量，将特解代入系统无阻尼自由振动方程可得：

由于{Φ}为自由振动的幅值向量，所以{Φ}不能为零，此时求解方程（4）转变为求解广义特征值的问题，式（4）中{Φ}有非零解的充要条件为：

式（5）称为求解变速箱箱体固有频率的特征值方程，特征值方程是关于ω2的n次线性代数方程，求解得到n个正实数根，，…，进一步通过这n个正数根可得到系统n个无阻尼固有频率ωi（i=1，2，…，n）。将ωi代入原式（4）求出该自由振动系统的第阶固有振型{Φi（}i=1，2，…，n）。

2　变速箱箱体自由边界条件模态分析

2.1　箱体三维建模

图1为某再制造公司提供的装载机变速箱箱体，为再制造毛坯。该变速箱箱体的材料主要为HT200，最大尺寸（长宽高）：1 080 mm×485 mm×595 mm，重量为274 kg.材料属性如表1所示。

图1　再制造变速箱箱体

表1　变速箱箱体材料属性

在对变速箱箱体建模的过程中，应该对箱体进行不同程度的简化[6]，以减少网格划分的数量和后续模态分析计算量。简化后的箱体三维模型如图2所示。

图2　变速箱箱体三维模型

2.2　箱体网格划分

网格划分越细，计算结果精度越高，但是，相应地，求解时间边长，对计算机要求也更高。结合实际情况，本文采用Solid187网格单元，Smart Sizing为7自动划分网格。网格划分结果如图3所示。

图3　变速箱箱体网格划分

2.3　箱体模态分析结果

本文采用分块蓝索斯法法提取变速箱箱体的模态结果。由于对变速箱箱体作自由模态分析，不对其添加任何约束，箱体前六阶模态频率计算结果和振型分析如表2所示，振型图如图4所示。

表2　箱体前6阶自由边界的模态频率值及振型描述

（续下图）

（接上图）

根据振型图，可以合理选择锤击点、响应点、及传感器布置点。为了减少支承装置的接触对分析结果的影响，支撑位置可以选择在箱体的节点位置；为了收集到箱体更多振动信息，锤击点、响应点应优先选择在多阶固有频率振动的方向上[7]。

3　柔性支承装置

为了提高变速箱箱体模态参数识别中模态锤击试验的准确性，需要构建箱体零件的柔性支承，以获得被试验对象的自由边界。根据箱体模态分析的结果，以及支撑点选取的原则，设计箱体采取图5所示的支撑方式。

图5　箱体柔性支承设计及支承方式

考虑到变速箱箱体质量较大，选择弹簧为主要受力元件，并通过导杆、导套来建立支撑。具体设计步骤如下[8]：

（1）弹簧材料

因弹簧主要承受箱体重量，为一般载荷，故选择第III类（载荷作用次数小于103次）碳素弹簧钢丝SL型。

（2）弹簧直径

式中，d为弹簧直径；Fmax为最大载荷；K为弹簧曲度系数；C为旋绕比；[τ]为许用切应力。

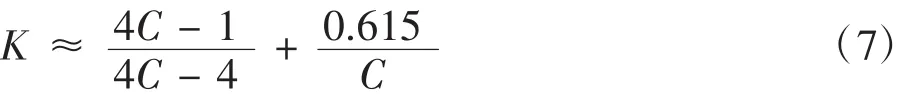
箱体质量274 kg，因此各个支承装置所受最大载荷Fmax≈ 274×10÷4≈ 685 N，旋绕比C=，通常取5~8，现暂取8，中径D=40 mm，弹簧直径d=5 mm.将C=8代入（7）得K ≈ 1.184，根据弹簧直径和材料属性查表得[τ]=830 MPa，代入（6）得：

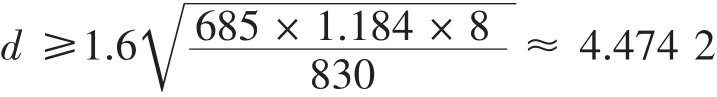
可以看到，所选择的弹簧直径d=5 mm，接近理论计算值，选取合理。

（3）弹簧圈数

为了使得支承装置具备一定的柔度，取变形量λ=50 mm.

式中，λmax为最大变形量，为弹簧材切变模量，查表为 80 000 MPa，代入式（8）得：

取n=8.

（4）弹簧弹性系数

将箱体柔性支承系统简化为弹簧质量块系统，如图6所示。

图6　箱体柔性支承系统简化模型

图6中，弹簧弹性系数为K0，质量快的质量为箱体的四分之一，不考虑空气阻力，假设系统为线性，则有：

式（9）中ω代表箱体柔性支撑系统的固有圆频率，由自由边界模拟的条件可知，系统的固有圆频率应该满足=102.18 rad/s，弹簧的弹性系数可由下式确定。

式（10）中，G为弹簧弹性模量；N弹簧圈数；D弹簧中径。

将弹簧圈数、弹簧中径等代入式（10）计算得

将ω＜2π×16.27 rad/s代入式（10）得K0＜715.19 N/mm，可以看到，弹簧劲度系数满足自由边界模拟的条件。

（5）导杆、导套

图7为柔性支承装置的设计图和加工后的实物图。为了使装置对箱体的支承更平稳，加工了4个同样的支承装置构成箱体的柔性支承系统。为了弹簧在箱体重量作用下不失稳，设计了导杆、导套，为了使装置与箱体接触面积更小，导杆顶端设计成顶针的形式。

图7　柔性支承装置设计及实物图

4　试验验证

实验仪器采用丹麦B&K公司的PULSE Labshop通用测试系统，详见表3.激励力锤标称灵敏度为2.149 mV/N，测量范围2 200 N，选用钢制锤头的频率范围可达5 kHz.单向加速度传感器的标称灵敏度为9.980 mV/N，频率范围 0.3 Hz~8 kHz.现场实物连接图如图8所示，结果如图9、表4所示。试验步骤：

（1）用力锤锤击箱体，获得激励和响应信号，为了使结果准确，重复4次取平均。

（2）根据频响函数计算出系统的各阶模态频率。

（3）观察响应信号与激励信号的相干性。

表3　试验设备

图8　实验现场

图9　一组试验中激励、响应信号及相干性

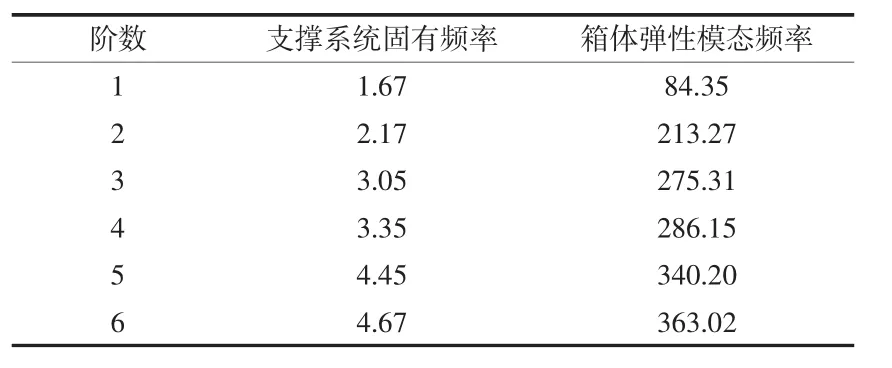
表4　箱体支承条件下各阶模态频率

从图9可以看到，激励信号没有产生明显的连击，说明箱体在外部冲击载荷作用下，没有产生快速回弹，柔性支承装置弹性合理。响应信号有明显的衰减过程，这说明柔性支承装置具有良好的柔度。从相干性图中可以看到，系统输入输出相干性较好，进一步证明柔性支承装置设计合理。

从表4可以看到，柔性支承系统的最高固有频率为4.67 Hz，箱体零件在柔性支承下的第一阶固有频率是84.35 Hz，柔性支承系统的固有频率远低于箱体零件第一阶固有频率的五分之一，表明所设计的柔性支承满足自由边界的要求。进一步从图10中对比发现，箱体自由边界理论模态频率（简称自由模态）和柔性支承下试验模态频率（简称试验模态）相差不大，因此，可以认为柔性支承装置对箱体模态参数提取结果的影响将会很小，自由边界条件的模拟能达到理想的效果。

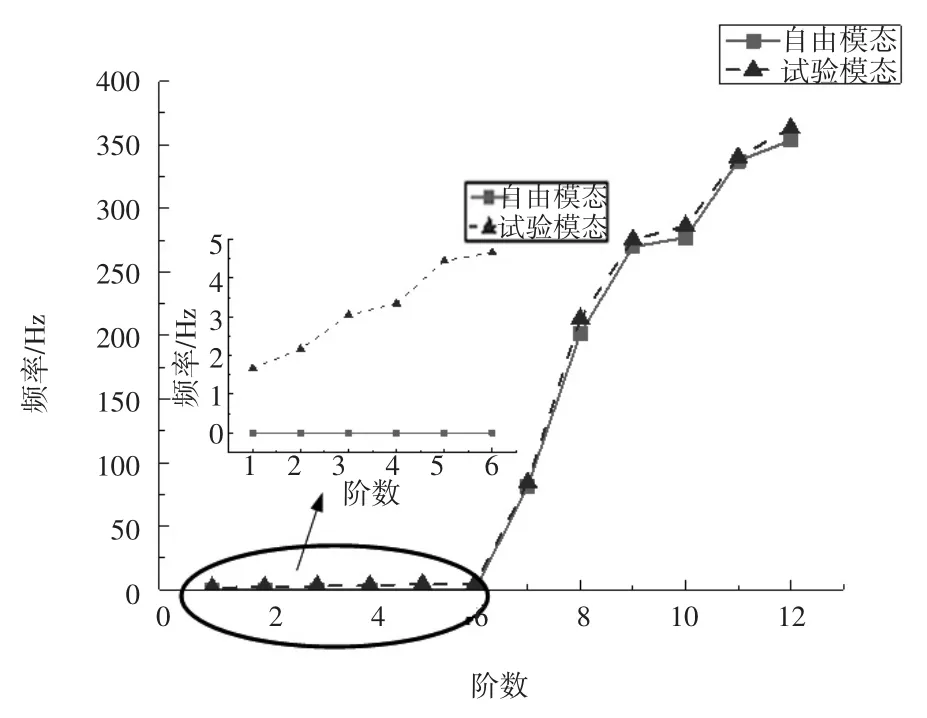
图10　自由模态、试验模态频率对比

5　结论

自由边界条件的模拟实质上是将外部因素对结构的约束和影响降到最低，使得对结构模态参数的提取结果更加准确。本文为了正确模拟再制造变速箱箱体的自由边界条件，以便准确获取其模态参数，设计了以弹簧、导杆、导套组成的柔性支承装置，并通过锤击试验得到了箱体在柔性支承作用下的各阶模态频率，通过比较箱体的试验模态频率和自由模态频率，证明了柔性支承装置满足设计要求，系统输入输出相干性也较好。