基于密码子特征的蛋白质序列图形表示

，

(浙江理工大学理学院，杭州 310018)

0　引　言

基于DNA和蛋白质序列的相似性分析，可以推断出不同物种之间的进化关系。所以分析序列的相似性是生物信息研究的重要课题[1]。在序列的相似性分析研究中，最常用的是序列比对方法，但由于序列比对方法的计算复杂度大。近些年，许多非序列比对方法被提出来并得到使用，其中一种就是图形表示方法[2]。

在生物序列数据库中，DNA和蛋白质序列是用字母序列表示的。在DNA数据库中，DNA序列是由A、C、G、T四种字母组成；在蛋白质数据库中，蛋白质序列是由A、C、D、E、F、G、H、I、K、L、M、N、P、Q、R、S、T、V、W、Y二十种字母组成[3]。图形表示方法是通过数学映射，把字母序列转化为空间图形，构建数学模型刻画图形之间的差异，进而推断物种之间的进化关系。图形表示法以其可视性好，计算简单，容易给出数值刻画等多方面的优点，受到研究者们的普遍关注[4-9]。

最初，Hamori等[10]利用随机游走，将DNA序列转化为3维曲线(H-曲线)表示。此后，许多研究沿着这个思路，将序列转化为1维、2维和4维曲线[11]。组成蛋白质序列的氨基酸有20种,与DNA序列的四种核苷酸相比，情况更为复杂，但蛋白质图形表示方法基本上都是DNA序列图形表示方法的推广，Rahman等[11]和Yu等[12]所采用的方法均是DNA序列图形表示方法的简单拓展。对于映射关系，氨基酸的理化性质[6,9,13-18]和氨基酸的循环排列[2,5,19-22]常常是研究者们建立映射关系的依据。

通过氨基酸的映射关系，构造迭代函数，将序列中的氨基酸映射成空间中的一个点，顺次连接这些点，就构成了蛋白质序列的图形表示[23]。对于迭代关系式，Jeffrey[4]使用相同参数的迭代关系式图形表示方法，随后，许多研究者使用同参数的迭代关系式[3,21,23-26]。此外，Ma等[8]首次提出异参数的迭代关系式，同样也取得不错的结果。结合Jeffrey[4]和Ma等[8]的观点，He等[27]提出广义混沌游戏表示方法。在把序列转化为曲线之后，数值刻画对于描述图形是必不可少的。图形表示只是提供视觉上的比较，但是数值刻画能够量化不同曲线之间的差异性。例如，在Yao等[7,28]通过几何中心来描述曲线之间的差异，在He等[21]采用距离矩阵的特征值来描述曲线之间的差异等。

本文考虑密码子碱基位置特征和氨基酸的疏水性特征，将氨基酸映射成为一个三维向量。结合Ma[8]和He等[27]结论，本文选取一种新的迭代关系式，获得新的3维图形表示方法。此外，为了比较曲线之间的差异，本文计算两个曲线之间的闵可夫斯基距离。应用新的3维图形表示方法到9个物种的ND5蛋白和12个物种的β-珠蛋白序列上，分析它们之间的相似性并推断相应物种之间的进化关系。将相似性分析结果与经典的多重序列比对算法ClustalW方法得到的结果做相关性分析，验证本文的方法有效性。

1　蛋白质的3维图形表示方法

1.1　氨基酸的三维坐标

四种碱基A、G、C、T可以组成64种三联体密码子。其中，61种密码子对应20种氨基酸，即通常所谓的遗传密码表。观察密码表可以看出，密码子的第一个位置和第二个位置的碱基几乎可以决定密码子翻译的是何种氨基酸。此外，密码子的第二个位置的碱基与密码子翻译的氨基酸的许多理化性质都有关联。所以，密码子的第二位碱基对于密码子的理化性质有着特殊的意义。由此，本文根据密码子第二位碱基的种类，将64种密码子分布在2维平面的四个象限内。

根据密码子第二位碱基确定三联体密码子所在象限，如图1所示，如果密码子的第二位碱基是A，本文将第二位碱基是A的16种三联体密码子全部放置在第一象限，类似的，如果第二位碱基分别是G、T、C，分别置于第二、第三和第四象限。选择第一个位置和第三个位置上碱基的映射关系如下：G→1、A→2、C→3、T→4。通过第一位和第三位碱基的映射关系，可以将61种密码子和3种终止密码子分布在2维平面内。例如密码子TGA，中间碱基是G，所以它放置在第二象限，又因为第一位置和第三位置上的碱基分别为T和A，根据映射关系T→4、A→2，所以密码子TGA的坐标为(-4，2)。根据这种规则,64个三联体密码子分别被放置在一个二维平面内(图2)。根据遗传密码表，将64个三联体密码子翻译成20个氨基酸与终止密码子(图3)。

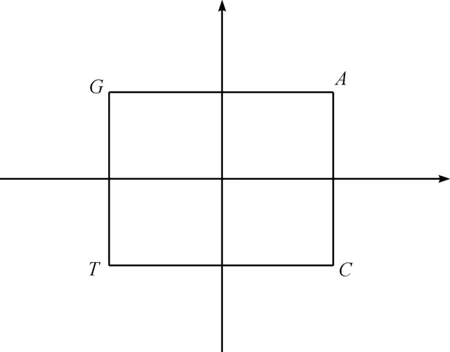
图1　第二个位置碱基决定密码子象限图

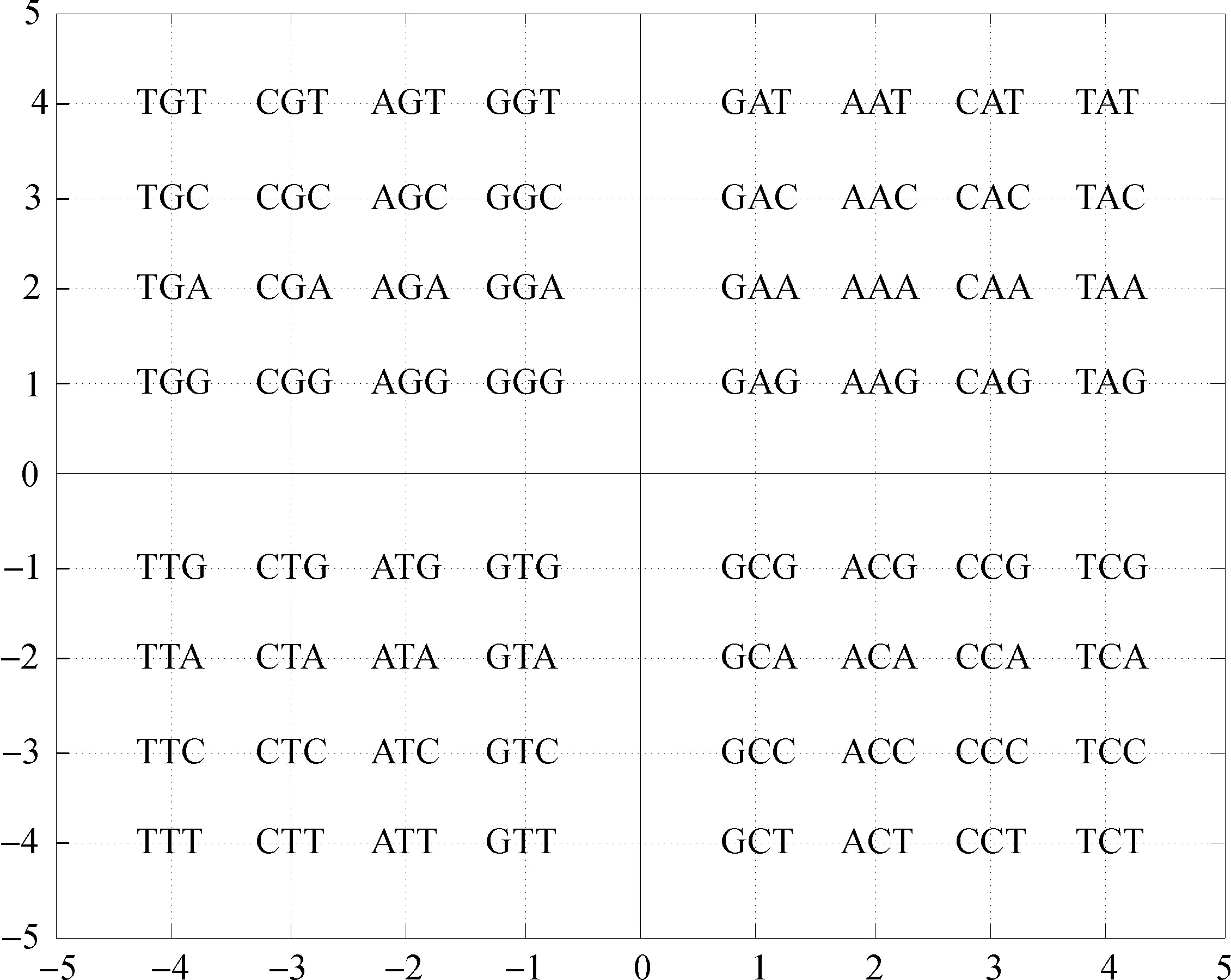
图2　密码子平面分布图

图3　氨基酸平面分布图

对于图3中的氨基酸，取同一氨基酸坐标的平均值作为该氨基酸的坐标，记作(P1，P2)。此外，由于氨基酸疏水性在保持蛋白质的三级结构上起作用，将氨基酸的疏水性指数值[29]作为第3维坐标，记作P3，构建氨基酸的3维坐标，记作(P1,P2,P3)，如表1所示(第3～5列)。

为了消除坐标值来源不同对结果的影响，文章对坐标值做了标准化处理，公式如下：

(1)

其中：a′是标准化之后的坐标值；a是标准化之前的坐标值；nmax和nmin为分别为坐标值中的最大值和最小值。根据式(1)可得新的3维坐标值，记作X，Y，Z，见表1(第6～8列)。20个氨基酸的坐标对应的20个向量，如图4所示。

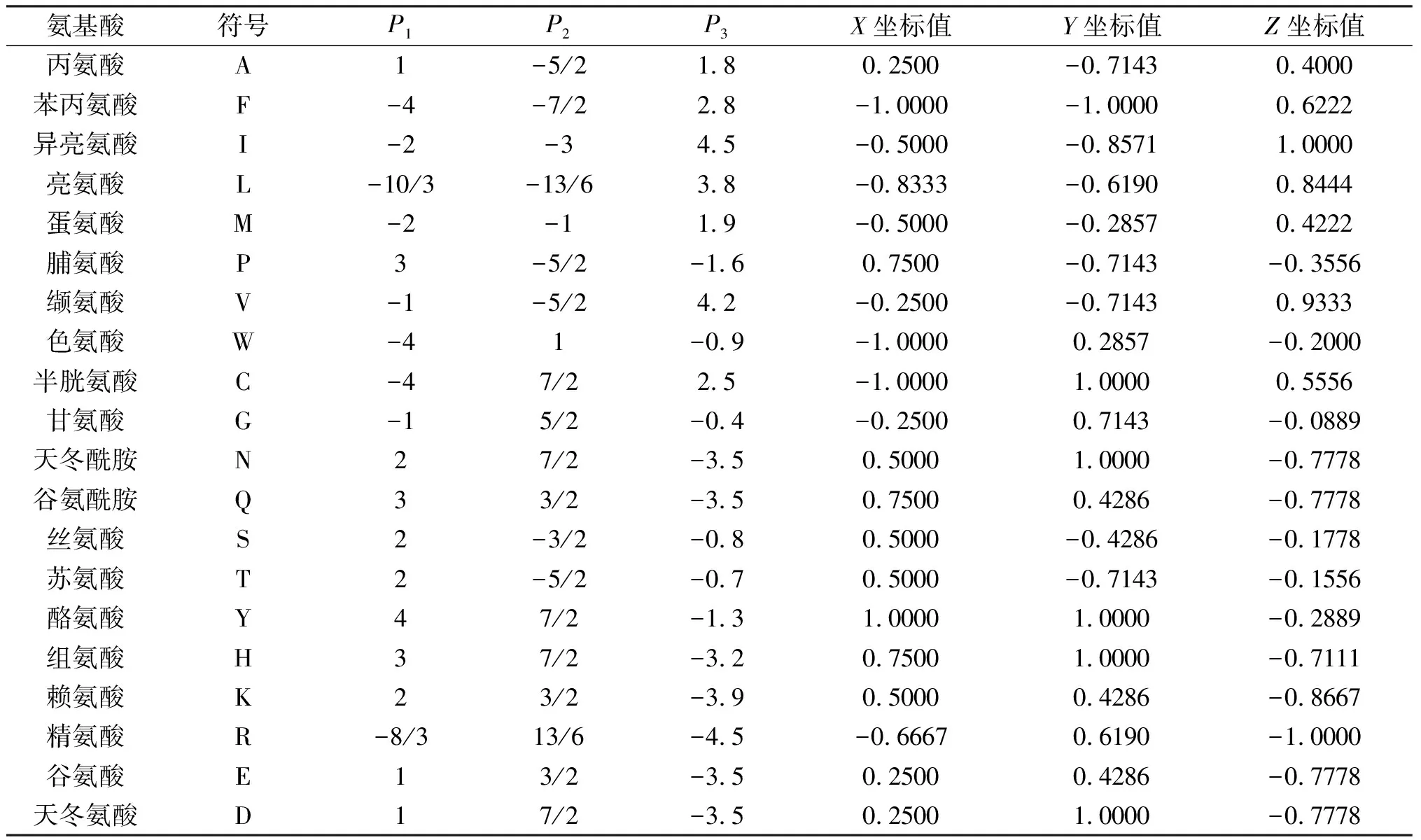
表1　氨基酸的3维坐标

图4　氨基酸对应的3维坐标向量

1.2　异参数迭代关系式

氨基酸是蛋白质的基本单元，通过氨基酸的3维坐标，笔者将蛋白质序列中的每个氨基酸转化为空间中的点，顺次连接这些点，得到蛋白质的3维图形表示。对于长为n的蛋白质序列s1s2s3…sn，每一个点(当i从1到n)对应的坐标Pi=(xi,yi,zi)，通过迭代关系式计算得出，通常迭代关系式的形式为：(本文选择P0=(0,0,0))

(2)

(3)

通过式3，氨基酸序列s1s2s3…sn被转化为P1,P2,P3,…,Pn共n个三维空间中的点，顺次连接这n个点，获得氨基酸序列的三维曲线。

1.3　图形表示的数值刻画

=(Xi,Yi,Zi)，(i=1…n2),

其次计算闵可夫斯基距离，计算公式为：

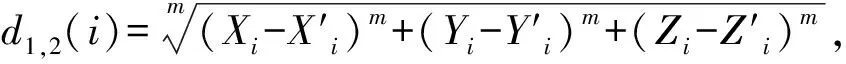
(4)

设k为剩余n1-n2个点之间的平均距离，所以两个序列的图形之间的距离公式为：

(5)

2　蛋白质序列的相似性分析

2.1　数据来源

本文将新的序列图形表示方法应用到9个物种的ND5蛋白(NADH dehydrogenase subunit 5)和12个物种的β-珠蛋白上，蛋白相关的信息见表2和表3。

表2　9个物种的ND5蛋白的相关信息

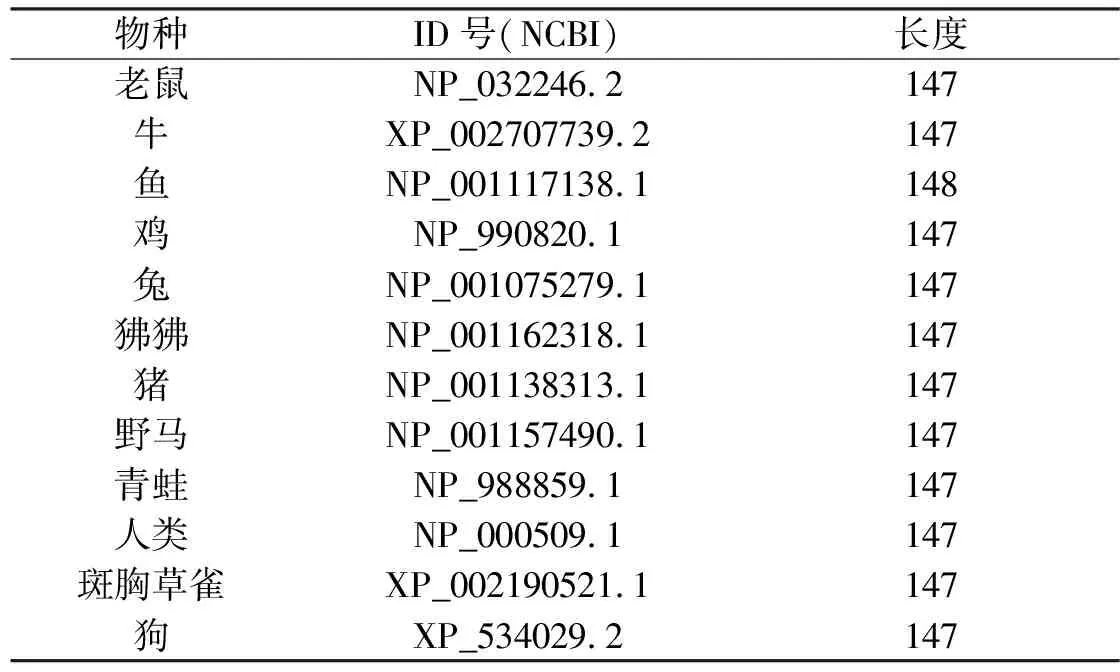
表3　12个物种的β-珠蛋白的相关信息

2.2　相似性分析

a) ND5蛋白序列

根据表2中9个物种的ND5蛋白数据，氨基酸的映射关系和闵可夫斯基距离公式，计算出这9个物种ND5蛋白的距离矩阵，如表4所示。ClustalW算法是目前被广泛应用的经典多重序列比对算法，为了说明本文方法的有效性，利用Megalign程序实现的ClustalW算法计算9个ND5蛋白的距离矩阵，结果如表5所示。

表4　基于本文方法得到的ND5蛋白的距离矩阵

表5　ClustalW算法得到的ND5蛋白序列的距离矩阵

表4和表5数据表明，较大的元素均在最后一列，表示负鼠与其他8个物种的进化距离最远；最小的元素分别为58.3(表4)和3.6(表5)，均表示鳍鲸与蓝鲸的进化距离在这9个物种中是最接近的；在表4中，人类、大猩猩、倭黑猩猩、黑猩猩之间的距离明显小于与其他物种的距离，同样也能够在表5中得出这样的结论。根据两个表中数据的特点，大致可以将9个物种分为四类，分别为人类、大猩猩、倭黑猩猩、黑猩猩；鳍鲸、蓝鲸；大鼠、老鼠以及负鼠，两表中数据表示的进化关系基本一致。

此外，根据本文方法的结果(表4)，运用生物信息学中构造进化树常用的UPGMA方法构造出进化树，结果如图5所示；根据ClustalW算法的结果(表5)，构造出进化树，结果如图6所示。

图5　基于本文方法构建的9个物种的进化树

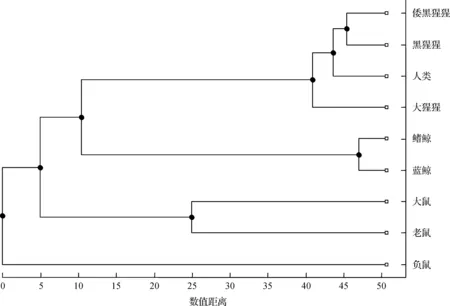
图6　基于ClustalW方法构建的9个物种的进化树

由图5和图6可以看出，本文方法构造的进化树与ClustalW方法构造的进化树在结果上完全相同，且两个进化树的分支结构上也非常相似，鳍鲸和蓝鲸均在同一个分支，人类、大猩猩、倭黑猩猩和黑猩猩在同一个分支，老鼠和大鼠在同一个分支，表示在9个物种里，鳍鲸和蓝鲸的进化距离最近可以归为一类，人类、大猩猩、倭黑猩猩和黑猩猩归为一类，老鼠与大鼠归为一类，与这些类距离最远的是负鼠，进一步证明本文蛋白质序列相似性分析方法与序列比对方法ClustalW算法具有一致性，说明本文方法是可靠有效的。

为了更直观显示表4和表5数据的关系，利用相关性分析两种方法得到的距离矩阵，结果如图7所示，图中横坐标为ClustalW算法得到的距离值，纵坐标为本文方法得到的距离值。结果显示，两组数据的相关系数为0.90，可见两种方法的结果具有很强的相关性。

本文进一步地分析两个距离矩阵每一行的相关系数，结果见表6(第2列)。为了比较，本文计算了文献[14,21,28]中结果与ClustalW方法结果(表5)的相关系数，结果见表6(第3-5列)。观察表6，对于所有物种，本文的结果与ClustalW算法结果的相关系数(第1行)明显高于文献[14,21,28]的结果与ClustalW结果的相关系数，同时，对于每个物种(第2-8行)，相关系数同样明显高于文献[14,21,28]结果与ClustalW算法结果的相关系数，对比结果说明本文方法具有明显的优越性。

图7　由表4和表5的数据作出散点图

相关系数本文结果文献[14]结果(表3)文献[21]结果(表4)文献[28]结果(表4)所有物种0.900.690.730.69人类0.930.920.820.86大猩猩0.930.700.750.78倭黑猩猩0.930.920.800.80黑猩猩0.930.930.790.70鳍鲸0.890.600.830.75蓝鲸0.890.700.840.86大鼠0.770.690.530.81老鼠0.730.640.420.74负鼠0.60-0.520.16-0.51

b) β-珠蛋白序列

根据表3中12个物种的β-珠蛋白数据，氨基酸的映射关系和闵可夫斯基距离公式，计算出这12个β-珠蛋白的距离矩阵，结果如表7所示。本文利用ClustalW算法计算这12个蛋白的距离矩阵，结果如表8所示。

表7　基于本文方法得到的β-珠蛋白的距离矩阵

表8　基于ClustalW算法得到的β-珠蛋白的距离矩阵

观察表7和表8数据可以发现，两个表中，最小的元素分别为27.2(表7)和5.7(表8)，表示狒狒与人类的进化距离在这12个物种中是最接近的；观察两表中人类与其他物种的距离(倒数第3列和倒数第2行)，除了野马、猪和人类的距离，青蛙，鱼和人类的距离略有差异外，人类与其他物种的距离基本相同。同时观察到两表中鱼、青蛙同其他物种的距离均比较大，从表7和表8显示本文方法结果和ClustalW方法结果基本一致。

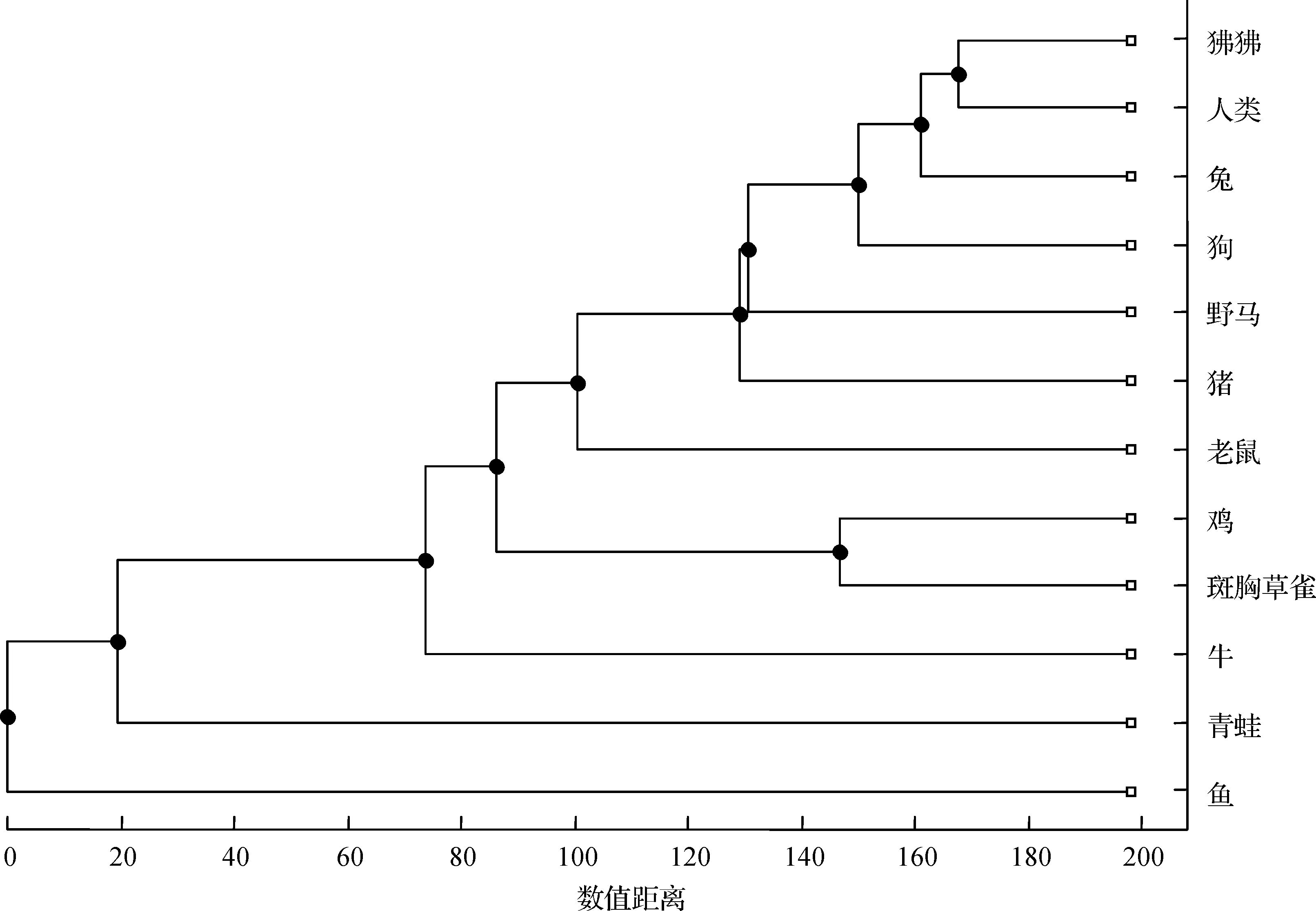
图8　基于本文方法构建的12个物种的进化树

此外，基于本文方法的结果(表7)构造出进化树如图8所示；基于ClustalW算法的结果(表8)，我们构造出进化树如图9所示。对比图8和图9发现，除了野马和猪，鱼和青蛙的位置不同外，其余分支的结构完全相同。

分析本文结果与ClustalW算法结果的相关性，本文以ClustalW算法得到的距离值(表8)为横坐标，以本文方法得到的距离值(表7)为纵坐标，作出散点图如图10所示，从图中可以看出两表中数据呈正相关，此外，我们计算出两个距离矩阵的相关系数为0.96，说明在β-珠蛋白数据中，本研究结果同样与ClustalW的结果相关性很强，两种方法的结果具有一致性。

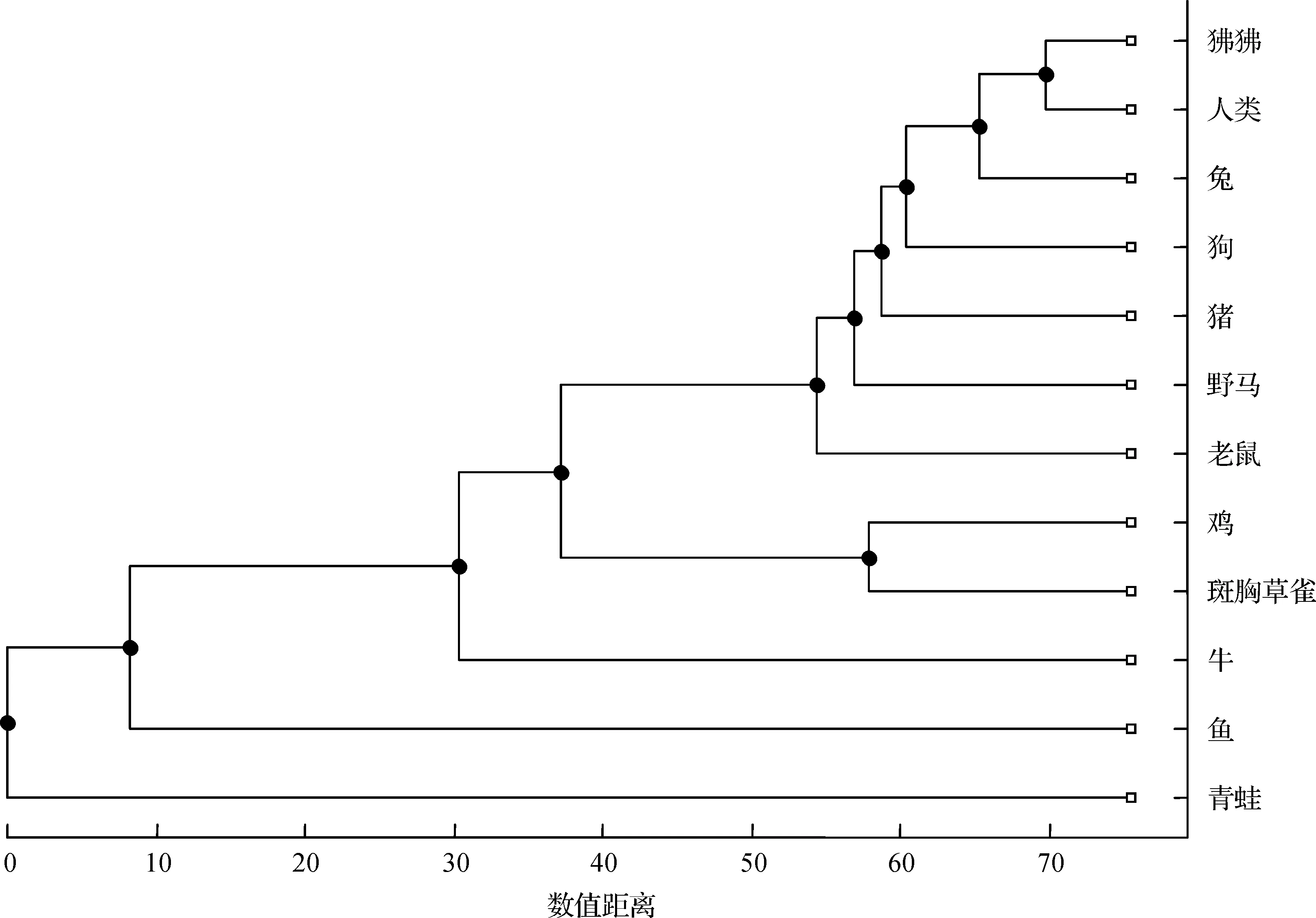
图9　基于ClustalW算法结果构建的12个物种的进化树

图10　表7和表8的数据的相关性

本文进一步地分析两个距离矩阵每一行的相关系数，见表9。结果表明，除了青蛙和鱼外，其他物种与ClustalW的结果相关系数均达到0.96以上。从9个物种的ND5蛋白和12个物种的β-珠蛋白两组数据的相似性分析结果中，因此本文的方法是有效可行的。

表9　不同物种与ClustalW结果的相关系数

3　结　论

本文利用密码子的碱基位置特征与氨基酸疏水性特征，提出一种新的蛋白质3维图形表示方法，并选取闵可夫斯基距离描述图形的差异性。运用本文方法，分析9个物种ND5蛋白的相似性和12个物种β-珠蛋白的相似性，并将相似性分析结果与ClustalW方法结果以及其他文献中方法的结果做比较，在ND5蛋白数据中，本文结果中与ClustalW算法结果的相关系数为0.90；在β-珠蛋白数据中，本文结果与ClustalW算法结果的相关系数为0.96。比较结果说明本研究的方法是有效可行的。