基于移动窗口和粒子群寻优的集成偏最小二乘改进算法

，　，

(浙江理工大学机械与自动控制学院，杭州 310018)

0　引　言

随着社会经济的快速发展，工业过程更加注重生产的安全、效益和环保，对过程关键参数的监测要求也愈加严格，仅仅依靠传统的检测技术已无法满足工业生产的多样化需求，在此背景下人们提出了软测量技术(软测量)。软测量通过建立过程辅助变量与主导变量之间的数学模型[1]实现对主导变量的预测，其中辅助变量是指那些易测且与主导变量有直接或间接联系的过程变量。软测量模型一般可分为模型驱动型和数据驱动型两大类[2-3]，在动态变化的工业生产过程中，数据驱动软测量建模优势明显[4]。数据驱动型模型又可细分为线性模型和非线性模型两类，在软测量中常采用线性模型[5]，偏最小二乘法(Partial least square,PLS)[6]是其中一种应用广泛的建模方法。相比于最小二乘法，PLS在处理多输入多输出数据时更具有优势，原因在于PLS中包含主成分提取的思想，可以在减小噪声干扰的同时，使有效信息更加集中，从而避免“维数灾难”的问题。

在实际工业生产中，时序数据会往往会呈现较强的非线性，将PLS非线性优化是当今研究的一个热点。根据非线性系统理论，如果系统的输出面光滑，那么任何非线性系统都可以通过多个线性模型进行逼近[7]，Kaneko等[8]由此提出了基于局部加权的偏最小二乘法算法(Locally weighted partial least square,LWPLS)。该算法首先将数据集划分成若干个子数据集并建立对应的局部子模型，然后利用集成学习的思想[9]给每个子模型匹配适当权值从而构成全局模型。与单个学习器相比，集成学习可以显著提高模型的泛化能力[10]。

本文针对工业过程中具有时序性、非线性、易突变等特性的数据，提出了以局部加权为主体框架的PLS建模方法。首先通过移动窗口(Moving-windows,MW)[11]对数据集进行划分，建立子模型；然后引入模型剪枝技术减少子模型间的冗余，进一步提高模型的效率；最后根据贝叶斯定理实现模型集成预测。由于模型性能受算法内部自定参数影响，本文引入粒子群算法(Particle swarm optimization,PSO)[12]进行参数自动寻优，确保模型性能最优，由此本文提出基于移动窗口和粒子群寻优的集成偏最小二乘改进算法EMWPLS_PSO。PSO是处理非线性连续优化问题、组合优化问题和混合整数非线性优化问题的有效优化工具，拥有算法简洁、易于实现、参数少且不需要梯度信息等优势[13]。PSO的适应度函数选择是参数寻优的关键，本文对此进行了研究。EMWPLS_PSO算法充分考虑时序数据的自身特性，利用移动窗口对数据集进行划分，辨识出各状态突变时刻。权值计算过程中结合TIM(Just-in-time)思想，得到的权值更加合理。冗余模型检查和PSO参数优化使最后的集成模型结构最优化，降低运算量，提高计算效率。

1　EMWPLS算法实现

EMWPLS算法的建模步骤为：首先采用移动窗口法对数据集进行移动分割，根据分割结果对各子数据集单独建模；然后引入模型冗余检测技术对建立的子模型进行剪枝；最后根据贝叶斯理论进行模型的集成。

本文使用以下三个指标进行模型性能评价[14]，以衡量预测值与真实值的契合度：误差平方根(The root mean square error,RMSE)、相对误差平方根(the relative RMSE,RE)和最大绝对误差(The maximum absolute error,MAE)，具体公式可以表示为：

(1)

(2)

MAE=max{|ypre,t-ytrue,t|,t=1,2,…,Nt}

(3)

其中：ypre,t和ytrue,t分别代表第t组测试集的模型预测值和真实输出值；Nt表示样本数。

1.1　基于移动窗口法建立局部模型

建立局部模型首先确定宽度为W的原始窗口，原始窗口中数据集记为Wini={Xini,Yini}，其中Xini∈RW*m,Yini∈RW*1分别表示输入变量和输出变量。利用PLS对Wini建模，得到模型fini。然后将窗口下移一步，新得到的数据集记为Wsft={Xsft,Ysft}。通过判定条件1判断模型fini是否适用于Wsft，若适用，则窗口继续下移直至条件不再满足为止。最后得到第一个子数据集{X1，Y1}，利用PLS对其建模可得到第一个子模型f1。

判决条件1可以表述为：

Eini=fini(Xini)-Yini

(4)

Esft=fini(Xsft)-Ysft

(5)

(6)

(7)

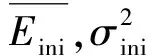
1.2　冗余模型删除

依照1.1小节介绍的方法继续建立f2，f3，…，至遍历所有数据。为了解决子模型建立过程中的模型冗余问题，本文引入一个删除冗余模型的步骤：当子模型个数大于2个时，通过判决条件2判定模型间是否存在冗余，若冗余则用新模型取代旧模型，并将旧模型删除。

判决条件2可以表述为：

将当前数据集分别代入新模型和旧模型，并计算其误差、误差的均值与方差，并利用t-分布和χ2-分布判定预测误差是否近似，用公式表示为：

Enew=fnew(Xnew)-Ynew

(8)

El=fl(Xnew)-Ynew

(9)

(10)

(11)

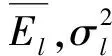
子模型的建立与冗余检验交替进行，直到遍历全部数据集，最终可得到L个子模型。整个算法的流程如图1所示。

图1　局部子模型构建算法流程

1.3　集成PLS算法实现

得到L个子模型后利用集成学习法对新样本进行预测，具体步骤为：a) 计算新样本在每个子模型中的估计值；b) 赋予每个子模型权值；c) 加权得到最终的集成学习预测值。这一部分算法的关键是如何定义步骤b)中的权值。本文使用Shao等[15]提出的方法定义权值。对输入xq，定义指标J(l)评价每个子模型的预测能力，J(l)越大表示第l个模型的预测误差越大，可用公式表示为：

(12)

(13)

(14)

其中：(x0,y0)表示历史数据中最新的一组数，γ是连接系数，且0<γ<1，γ的大小和x0与xq之间的距离有关，可表示为：

γ=exp (-ρd(xq·x0))

(15)

其中：ρ为可调参数。

类似地，sk和xq与xk之间的距离有关，计算公式为：

sk=exp (-d(xq·xk)/σd)

(16)

其中：d(·)表示两点间的欧氏距离，σd表示xq与历史数据的距离的方差。

由于J(l)代表模型的预测误差，J(l)越大则表示分配给第l个模型的权值应当越小，本文用g(l)表示：

g(l)=exp (-ψJ(l))

(17)

其中:ψ为可调参数。

最后对所有子模型集成：

(18)

其中：fl(xq)是xq在第l个子模型中的预测值，P(fl|xq) 是由贝叶斯推理得到的后验概率。

(19)

其中：P(fl)和P(xq|fl)分别代表先验概率和第l个模型能准确预测xq的可能性。

(20)

P(fl|xq)=g(l)

(21)

其中：Nl表示建立第l个模型所用到的样本数量。

综合式(18)—(21)，可以得到

(22)

2　基于PSO的参数优化

2.1　模型参数对预测效果的影响

在利用EMWPLS算法建模的过程中会涉及4个关键的可调参数：移动窗口初始大小W、邻近点数量K以及模型集成时的参数ρ和ψ。移动窗口初始大小W与最终构建的子模型数量密切相关，若W较大，则可能导致不同状态的数据被归为一类，从而会影响子模型预测效果；反之若W太小，子模型数量过多，则会增加模型的复杂度、降低运行效率。类似地，如果K太小，可能导致模型过拟合，增大模型的预测误差；反之若K太大，则会影响相连时刻的数据对各子模型预测能力的判断。在对子模型进行集成时，ρ和ψ大小也同样关键。由式(15)可知，如果ρ的值较大，则相应的γ很小(ρ无穷大时，γ趋向于0)，导致式(12)中J1在J中所占的比例较小。同理，式(7)中的ψ不宜过大，因为当ψ无穷大时，g趋向于0，而在式(22)中可以看出g(l)不能都为零(分母不能为零)。

本文以标准数据集中的abalone数据集[17]为例，分析四个参数对模型预测精度的影响。图2—图4分别给出了四个参数与模型预测误差指标RMSE、RE以及MAE的对应关系曲线，从图中可以观察得到：四个参数对预测效果均有较大影响，且它们之间呈现出较复杂的非线性关系。对于不同数据集，其影响关系也不同。因此本文提出一种基于PSO进行参数自动寻优的解决思路。

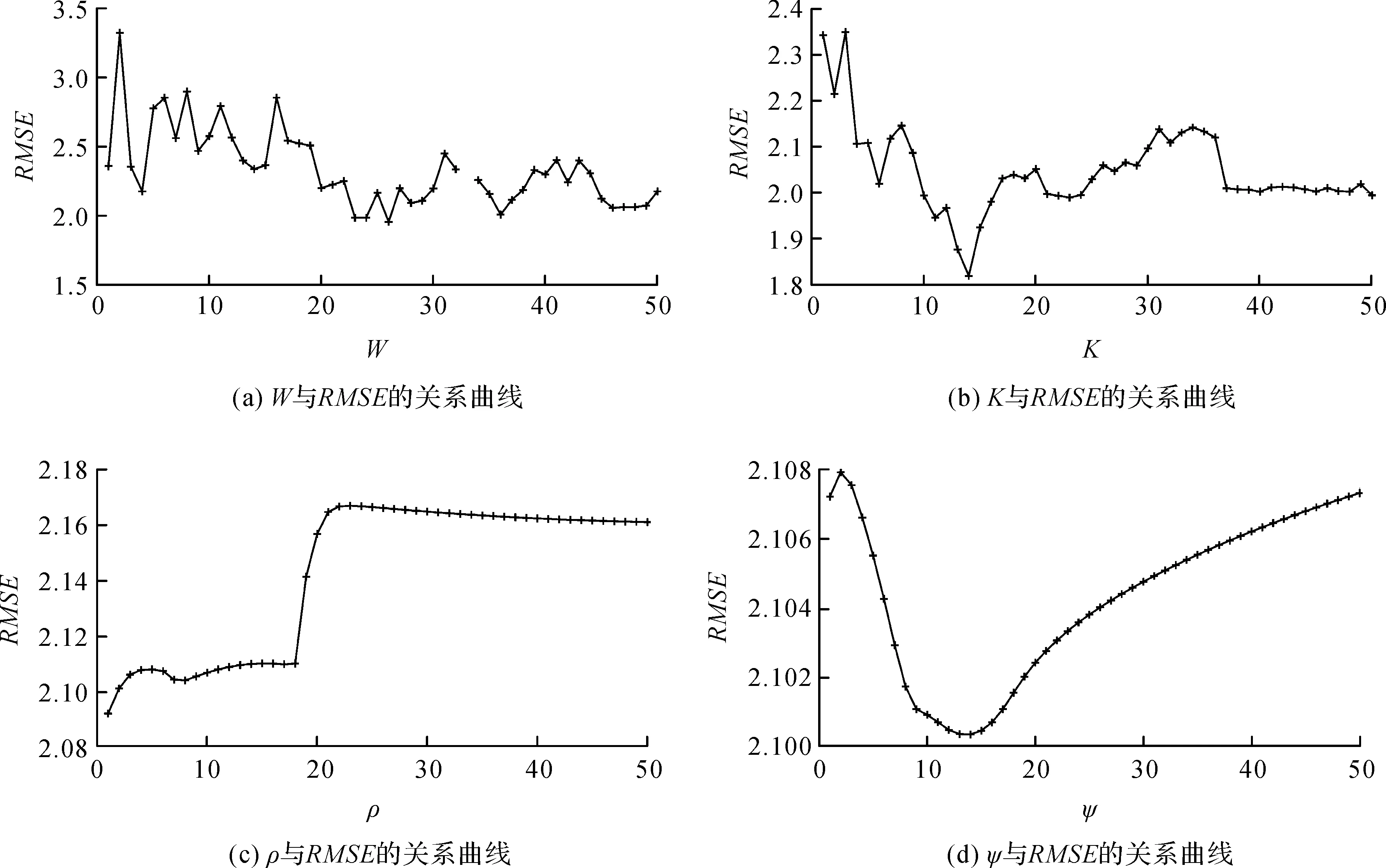
图2　W,K,ρ,ψ四个参数与RMSE的关系曲线

图3　W,K,ρ,ψ四个参数与RE的关系曲线

图4　W,K,ρ,ψ四个参数与MAE的关系曲线

2.2　粒子群参数寻优

2.2.1适应度函数选择

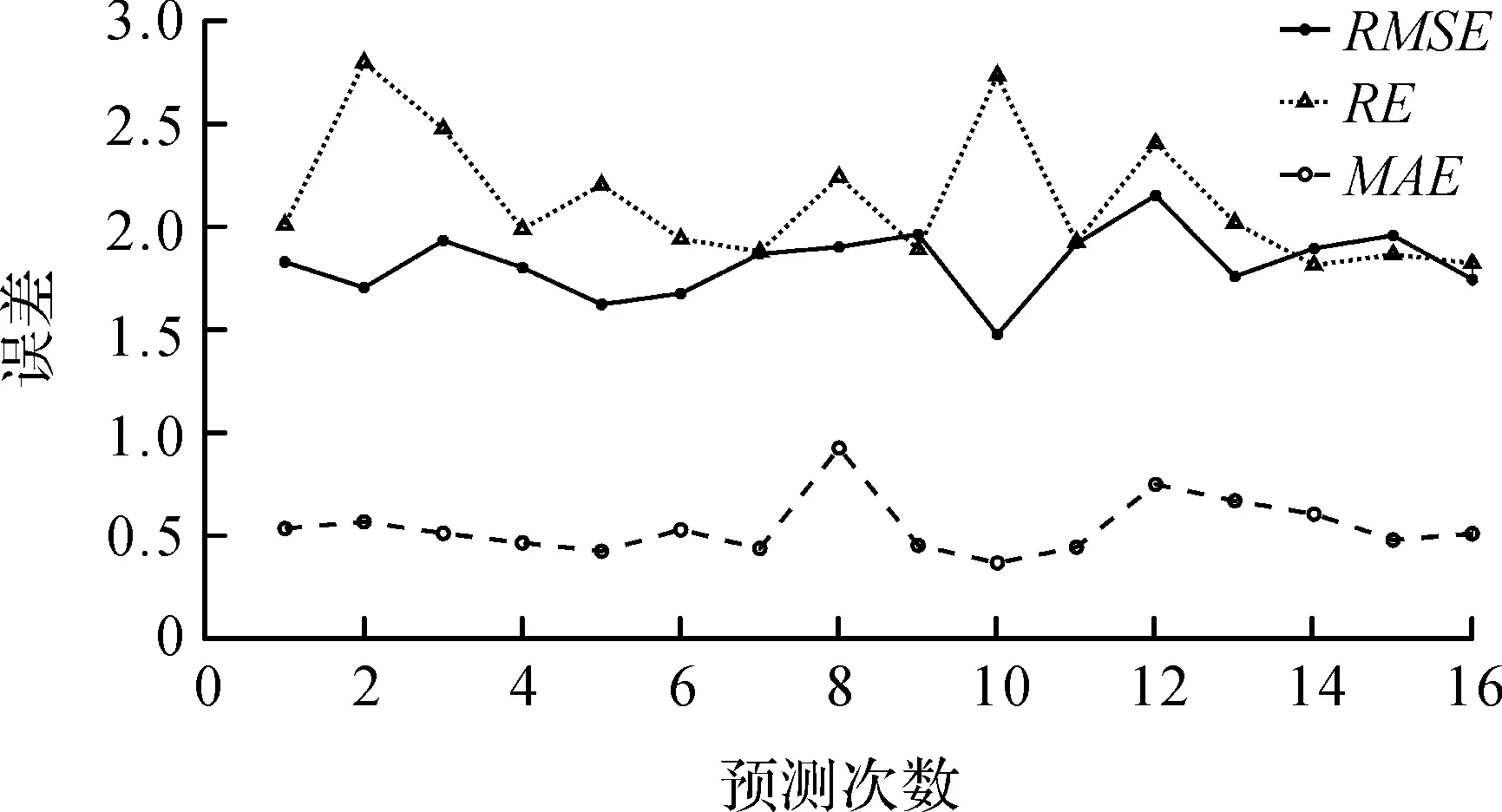
图5　误差变化与RMSE、RE、MAE之间的关系图

在使用粒子群算法时适应度函数的选择是一个关键的步骤，本文选用RMSE、RE、MAE来评价模型的性能，所以将其作为备选适应度函数,由于MAE受单个样本影响较大，故不考虑其作为适应度函数。分析式(1)—(2)可以得到结论：对于同一个模型而言，预测结果的RMSE、RE的变化趋势并非一直保持一致，它受误差统计分析时|(Ypre,t-Ytrue,t)/Ytrue,t|>1 的样本数在所有样本中所占比例影响，当其比例高时RE的值可能会随着RMSE的减小反而增大。图5显示了abalone数据集在16组不同参数下得到的对应EMWPLS模型的RMSE、RE、MAE指标曲线，从中观察发现RMSE和RE的变化趋势并不一致(为对比二者趋势，图中RMSE的数值已放大10倍，RE数值放大5倍)。图5中曲线对应的具体数值详见表1。在这16组数中第10组的RMSE最小，第14组的RE最小。这表明分别用RMSE和RE作为适应度值进行参数寻优会得到不同的结论。

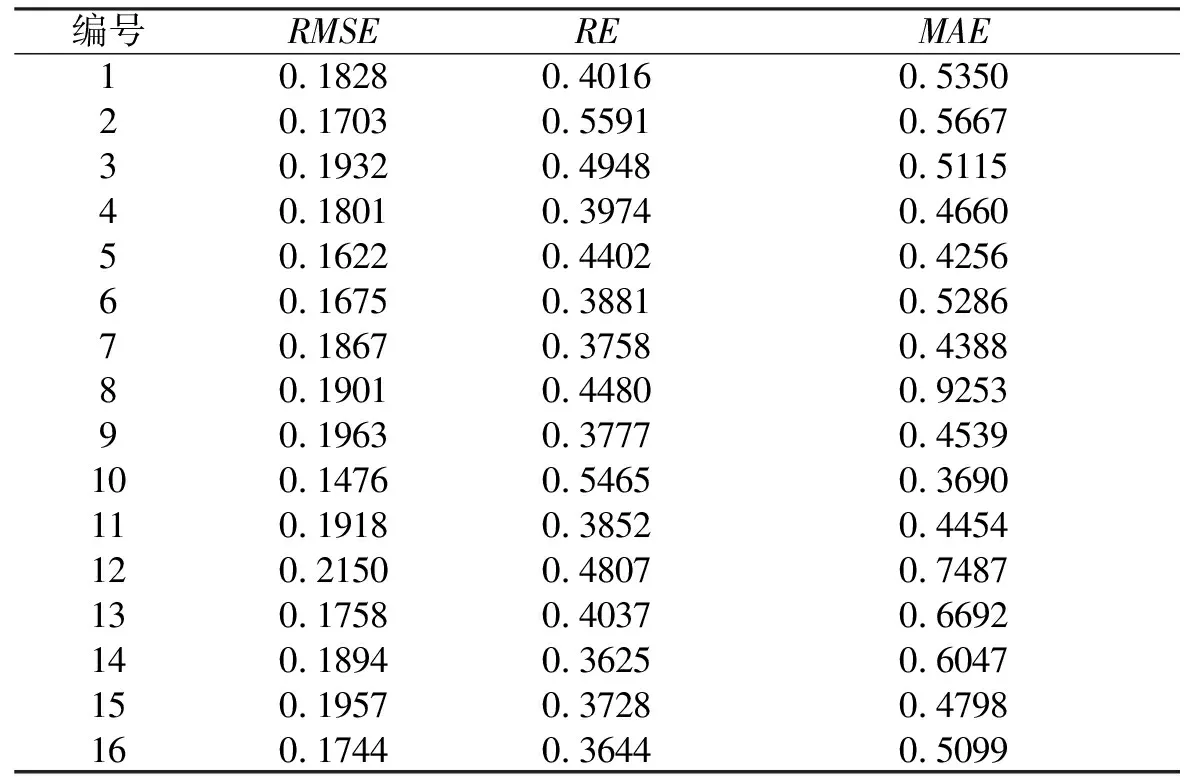
表1　不同参数下abalone数据集的RMSE、RE、MAE数值

可见适应度函数的选择会直接影响参数的寻优结果。选取几组不同参数对abalone数据集进行EMWPLS_PSO建模，并依照式(1)—(3)计算出各组的RMSE、RE、MAE，选出RMSE相同RE不同、RMSE不同RE相同、RMSE和RE都不相同的两两对应的几组数据，记录于表2，并绘制图6—图8的曲线。通过比较可发现若单独选其中一个值作为适应度值RMSE比RE更合适。当RMSE值相同时，RE值越小则模型效果越好。根据上述结果笔者认为将RMSE和RE相结合效果更佳。本文提出Z=p*RMSE+(1-p)*RE作为适应度函数，其中p为连接系数，且在Z中RMSE应该占更大的比重。

表2　不同参数下模型的RMSE、RE、MAE值对比

图6　RMSE相同RE不同时实际输出与预测输出

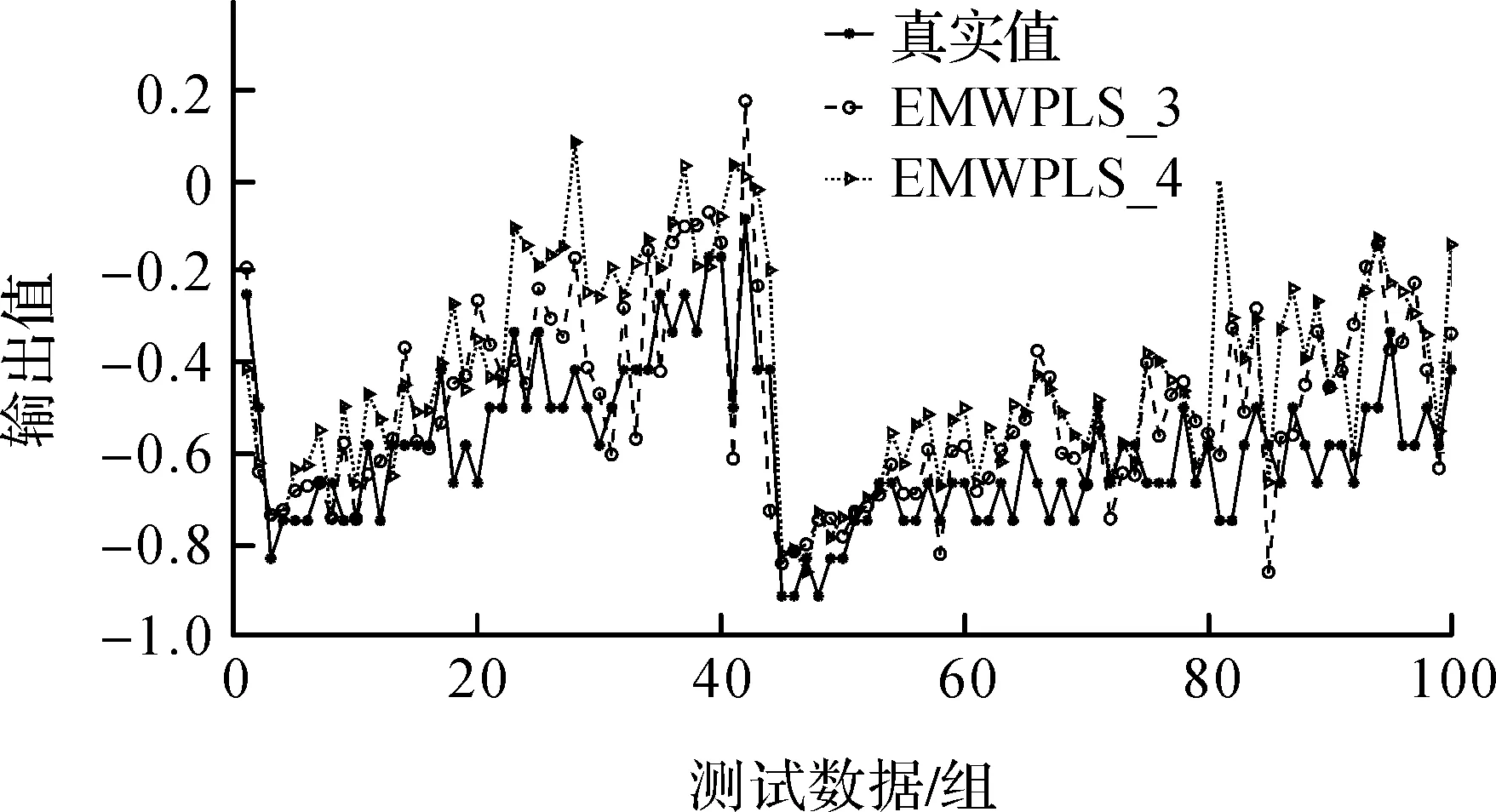
图7　RMSE不同RE相同时实际输出与预测输出

图8　RMSE、RE均不同时实际输出与预测输出

2.2.2寻优过程

本文选择粒子群算法的适应度函数为：Z=p*RMSE+(1-p)*RE，优化目标为W,K,ρ,ψ四个关键参数。基于粒子群算法的参数寻优过程如下：

a) 参数随机初始化(种群粒子数设为20，迭代次数设为50次，各参数设置合理上下限，初始位置与速度在参数上下限范围内随机给定);

b) 计算适应度值，更新粒子的历史最优和全局最优位置；

c) 根据迭代公式更新粒子的位置和速度,如果超出边界值，则赋予其边界值;

d) 判断是否达到最大迭代次数和全局最优位置满足最小界限，若不满足则返回步骤b)，反之结束寻优。

3　工业数据集测试

本文使用工业数据集Debutanizer_data[18]验证模型效果，该数据集共700组样本，7个输入1个输出，将前500组样本作为训练集，后100组样本作为验证集，最后100组样本作为测试集。表3、表4记录了其中6次粒子群寻优得到的参数及其误差分析，选取结果最好的第一组参数作为EMWPLS_PSO的最终参数，并与常规PLS以及BP算法进行对比。

表3　Debutanizer_data数据集重复6次寻优参数记录表

表4　Debutanizer_data数据集重复6次寻优误差分析表

图9给出了EMWPLS_PSO算法与常规PLS、BP算法预测结果的对比曲线。图9中点越接近中间的Y=X直线说明模型的预测值与真实值越吻合，模型预测效果越好。将真实值记为Yreal，预测值记为Ypre。记diff0.1=P(|Yreal-Ypre|≤0.1)，常规的PLS得到的diff0.1为0.75，EMWPLS_PSO对应的diff0.1为0.93。记diff0.05=P(|Yreal-Ypre|≤0.05)，常规的PLS得到的diff0.05为0.45，EMWPLS_PSO对应的diff0.05为0.785。可以得到结论：集成移动窗口技术对常规PLS的预测精度有很大的提高。图9(b)是PLS模型、EMWPLS_PSO模型的预测值与真实值的对比图，通过对比可发现相对于PLS，EMWPLS_PSO的预测趋势更准确，与真实值更吻合。图9(c)—(d)是同作为非线性算法的BP与EMWPLS_PSO的预测结果对比图。其中BP的diff0.05为0.47，diff0.1为0.68。由对比曲线可以看出，EMWPLS_PSO的预测效果也优于BP。表5记录了PLS、EMWPLS_PSO和BP算法的RMSE、RE、MAE值，从中可以得出结论，较之常规PLS和BP算法，EMWPLS_PSO的预测误差最小。

图9　EMWPLS_PSO与常规PLS、BP算法的预测结果对比

EMWPLS_PSORMSEREMAEPLSRMSEREMAEBPRMSEREMAE0.050.240.180.090.410.250.080.540.25

本文将EMWPLS_PSO与改进前的PLS算法作纵向比较，同时横向比较了非线性的BP算法。EMWPLS_PSO算法在PLS基础上性能有极大的改善，较好地克服了PLS对非线性数据拟合能力差的问题。同时，相比于纯数据驱动的传统神经网络建模方法，在小样本建模方面EMWPLS_PSO拥有更高的预测精度。

4　结　论

本文将移动窗口技术与集成学习的思想相结合，提出一种EMWPLS_PSO软测量算法。在利用移动窗口法建立局部模型时，增添了局部模型的冗余检查及删除的步骤，更好地提高了模型的效率和性能。此外，该模型同时应用时域和空间域上的历史数据对动态数据变化趋势进行预测，在避免过度拟合的同时进一步提高了模型的准确性。最后，为了保证模型在处理不同数据时拥有最佳预测精度，本文采用粒子群算法对参数进行自动寻优。通过以上技术的结合，很好地改善了PLS对线性相关性较差的时序数据的建模效果。