满足最小装机功率下的船舶波浪增阻数值计算研究
2018-07-11董国祥高玉玲李传庆
贾 腾, 董国祥, 高玉玲, 李传庆
(上海船舶运输科学研究所 航运技术与安全国家重点实验室,200135)
0 引 言
在船舶能效权衡工作组(Working Group on Energy Efficiency Measures for Ships,EEWG)第1次会上,国际船级社协会(International Association of Classification Societies,IACS)提出了最小装机功率概念,在海洋环境保护委员会(Maritime Environment Protection Committee,MEPC)61会议上,最小装机功率被明确。在MEPC 61/5/32提案中IACS指出[1],当强制实施船舶能效设计指数(Energy Efficiercy Design Index,EEDI)时,船舶设计者若想船舶符合其标准,可选择降低船舶设计航速,但是航速的降低势必导致船舶推进功率的降低,这样的船舶如果遇到极端海况,可能无法安全驶出危险区域。故此,IACS建议在EEDI规则中增加保证船舶安全性的条款[2],减少船舶在极端海况下的安全隐患。
要求得使船舶在极端海况下以最小前进速度行进所需的功率,就需要计算船舶在极端海况下受到的总阻力,包括空气阻力、静水阻力和波浪增阻。其中波浪增阻的计算是较为困难,且海况等级越高尤其是在极端海况下,波浪增阻在总阻力中占的比例较大,因此对计算波浪增阻的方法进行研究具有实际意义[3]。
船模试验法和数值计算法是目前研究波浪增阻的主要方法。关于波浪增阻的数值计算,目前主要有基于二维切片理论、基于三维时域理论和基于黏流理论的3种数值方法[4]。基于黏流理论的数值方法主要是基于雷诺平均N-S方程的离散,与基于势流理论的数值方法相比,能处理非线性流动现象,在处理甲板上浪及大幅运动等强非线性问题上具有极强的优势,但是该类方法对计算性能要求很高,且计算速度较慢。相对于二维切片理论和黏流理论,基于三维时域理论的预报方法理论上计算效率更高。
利用基于泰勒展开边界元方法对目标船在高速和低速下的波浪增阻进行计算,并与试验结果进行对比,分析产生差异的原因。
1 计算方法
边界元方法[5]可分为常值面元法和高阶面元法,运用三维泰勒展开边界元方法[6]会使非光滑边界处切向诱导速度的计算精度得以改进。
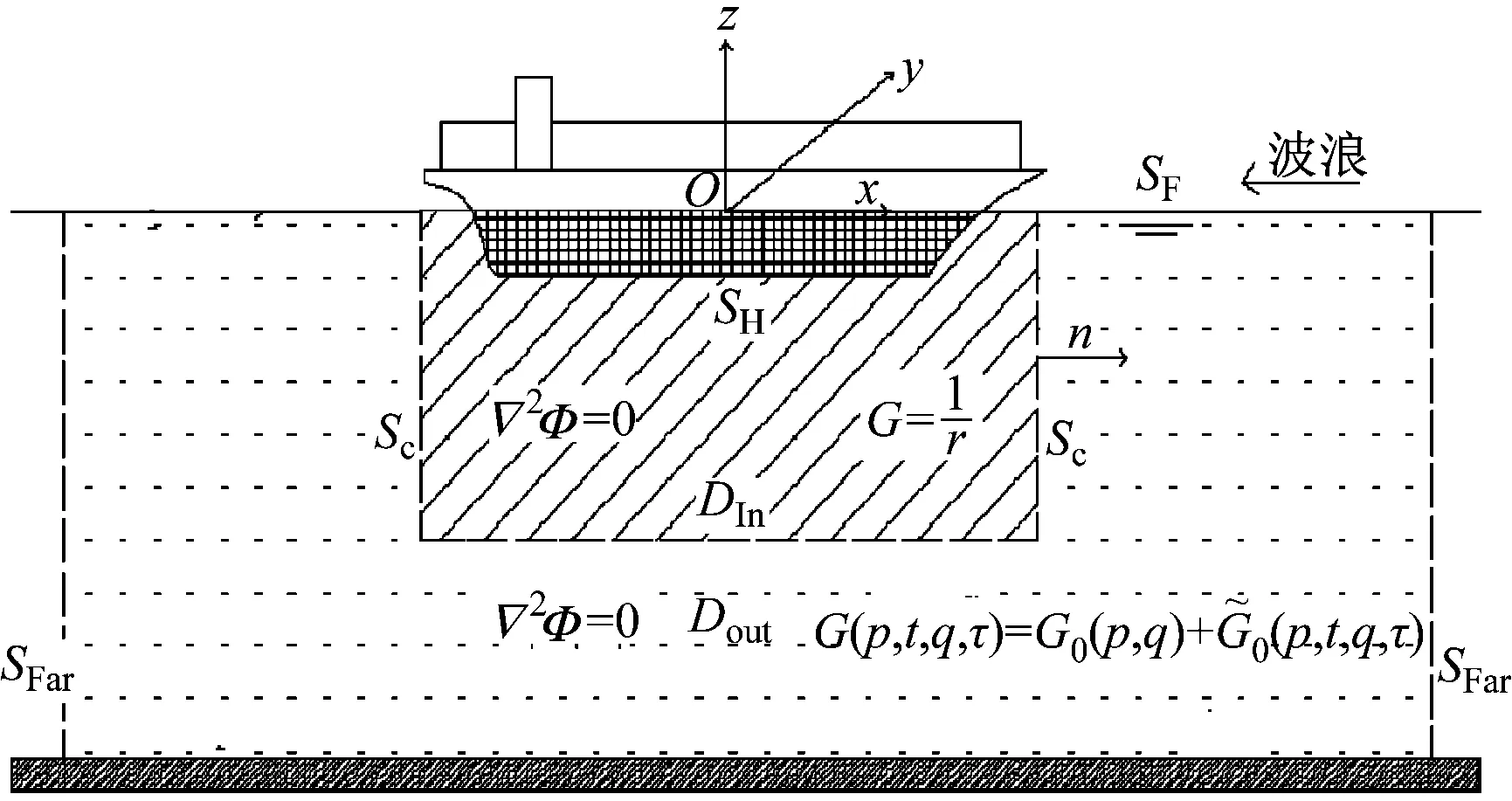
图1 坐标系及边界示意
在有航速定解问题中,物面边界条件及自由面边界条件中均涉及速度势的高阶导数,利用泰勒展开边界元方法,能精确求解非光滑流域边界处流体运动质点切向诱导速度,为有航速定解问题求解提供了技术基础。同时利用积分格式的自由面条件,解除了离散网格与时间步长需匹配的限制,在一定程度上提高计算效率。
建立平动坐标系O-xyz(见图1)。xOy平面为静水面,z轴垂直向上。无限水深中船舶以速度u沿着x正方向前进。匹配面SC将x流域D分成内域DIN和DOUT。DIN流域边界包括船体湿表面SH,匹配面SC,内部自由面SF。Dout流域边界包括匹配面SC,剩余自由面SF及无穷远控制面。
对于有航速定解问题,总速度势可分解为
φ=Φ+φd+φI
(1)
在内域中定解问题为
(2)
在外域中定解问题为
(3)
式(2)和式(3)中:vj为船体6个自由度的运动速度。
运用格林第三公式及边界条件,可得到源-偶混合分布方法和分布源方法的边界方程。三维分布源方法边界积分方程为
(4)
式(4)中:σ为分布源源强;G为格林函数;s为浮体湿表面积。
2 模型试验简介
耐波性试验设备采用四自由度适航仪及非接触式超声波浪高仪,伺服式倾角仪及加速度传感器。造波机可造的最大波高0.3 m,频率范围为0.25~2.0 Hz。试验在深水拖曳水池中进行,拖曳水池水深4.2 m,长和宽分别为192 m和10 m。
在试验准备阶段按照要求调整好船模惯量,使船模不仅满足质量要求,还满足重心和纵向转动惯量要求。将模型与试航仪连接,应用四自由度适航仪拖曳模型,采用四自由度适航仪测量纵摇、垂荡和阻力,浪高仪测量波高,加速度传感器测量垂向加速度。
根据相应航速下测量的静水中阻力,通过与规则波中阻力比较可得到波浪增阻。
试验对象为57 000 DWT 散货船,船模垂线间长为5.829 m,其主要参数见表1。

表1 散货船基本参数
3 数值计算
船体计算模型见图2,模型坐标系原点建立在船体中纵剖面与水线面的交线中部,模型为船体左舷半船模型。模型网格见图3,除艏部区域和尾轴管区域采用三角形网格,其他区域均采用四边形网格,自由面网格划分选取45。根据经验,纵摇惯性半径和艏摇惯性半径均选取0.25Lpp。选取了2个航速,分别为6 kn,11 kn,每个速度下从波浪频率在0.366~1.035中取19个工况,各工况下的波高设定参照试验波高。计算过程中每周期步长设置为30 s,模拟周期个数设置为9。

图2 船体模型

图3 船体面元网格
4 数值计算与试验结果对比
采用基于三维泰勒展开边界元方法计算得到低航速和高航速下的波浪增阻与模型试验结果对比见图4和图5,两图均为波浪增阻频率响应曲线,横坐标和纵坐标分别为波长船长比和无因次波浪增阻。
通过对比发现,在低航速和高航速下计算结果与模型试验结果的规律性一致,随着波长与船长比的增加,波浪增阻均呈现先增大后减小的趋势,均在波长与船长比为1.0附近达到峰值。航速为6 kn时,波浪增阻在波长船长比为1.0时达到峰值,数值计算结果比试验值略大;航速为11 kn时,波浪增阻在波长船长比为1.2处达到峰值,数值计算结果与试验值吻合性较好。
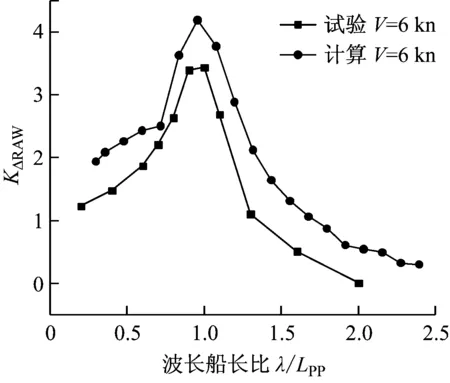
图4 航速为6 kn时波浪增阻频率响应曲线
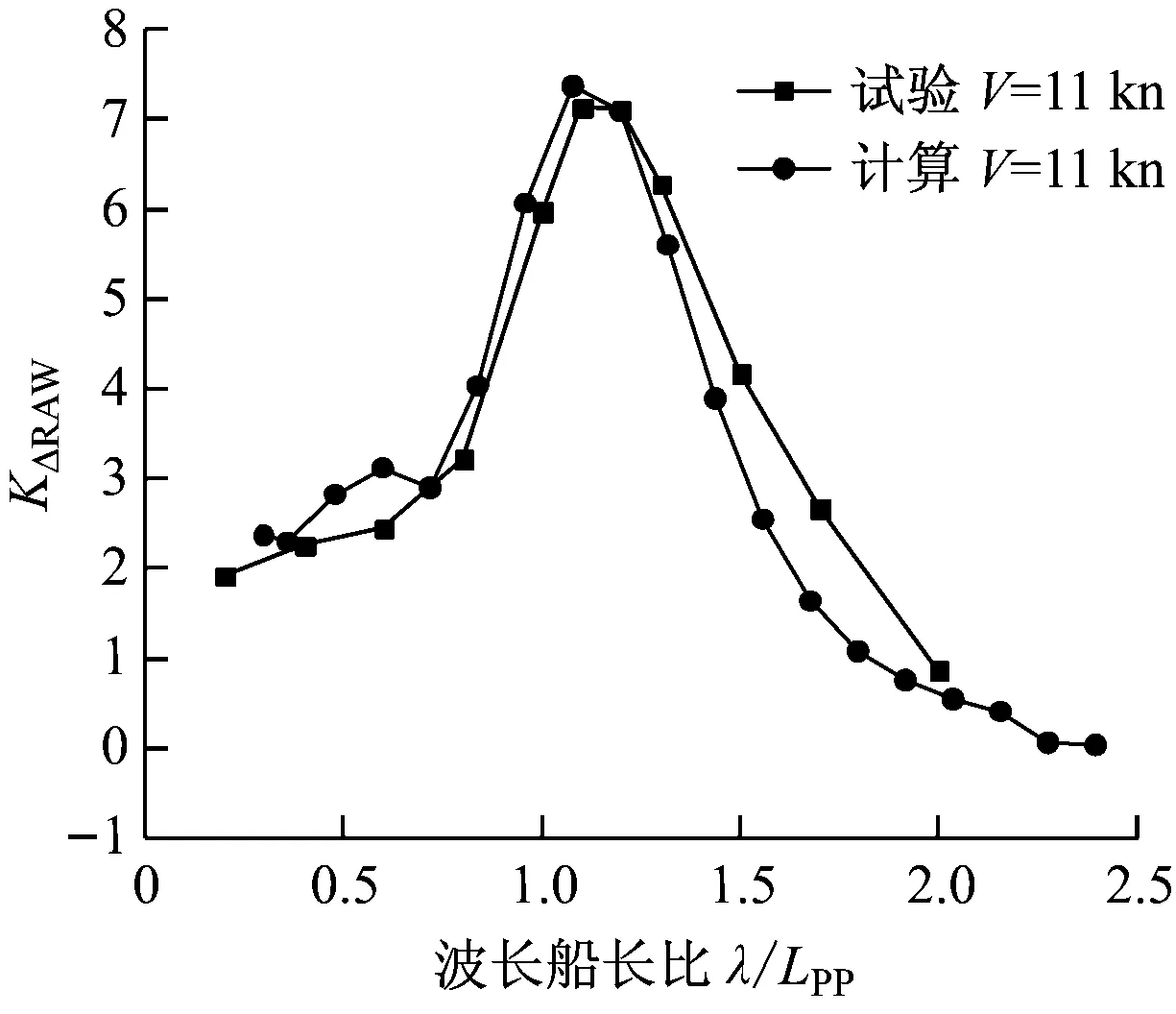
图5 航速为11 kn时波浪增阻频率响应曲线
5 结 语
利用基于泰勒展开边界元方法的数值计算方法对一般散货船在低航速和高航速下的波浪增阻进行数值计算,将数值计算的结果和模型试验得到的波浪增阻进行对比分析。通过对比发现:数值计算结果与模型试验得到的结果规律性一致,航速较高时计算结果与模型试验的结果吻合性较好,但在低航速时计算精度略低,计算结果比试验值略大,采用该方法对最小装机功率下的波浪增阻进行评估较为保守。
