基于振动的导管架平台结构健康监测技术研究

安振武

(中海油能源发展装备技术有限公司 天津300452)

0 引 言

根据调研统计，中海油目前服役的导管架平台已超过 240座，其中近 60座已经或将要达到它们的设计寿命，正步入后服役期，这些平台随着服役年限增长，由于环境腐蚀、材料老化、构件缺陷、机械损伤、突发灾害、疲劳及裂纹扩展的损伤积累等原因，平台抗力衰减现象日益严重。抗力衰减会导致平台可靠性降低，甚至发生平台倒塌事故，一旦发生平台结构安全事故，无论是人员损伤还是经济损失，所造成的后果都是十分严重的。因此，为确保导管架平台的安全运营，需要对其结构健康状态进行实时监测。

结构健康监测的重要目的是根据监测数据对平台结构的损伤进行评估，传统的无损检测/监测方法基本上是对局部结构损伤进行检测评估，如目测、X光检测、超声检测、磁粉和热成像等方法，这些检测方法决定了它们的非全局性和非实时性，不能满足现代大型工程结构对结构安全性进行全面监测、实时评估的要求。相比而言，振动检测技术由于其可以实现实时监测，并具有能够在整体上评估结构损伤等优点[1]，受到广泛重视。

1 振动检测技术

振动检测是对工作状态下的结构状态进行检测，通过检测可以得到结构的动力响应数据，依据相应的参数识别方法得到需要的结构动力参数，包括固有频率、阻尼、模态等，以此对结构进行损伤判定。振动具有整体检测与识别的能力，可借助有限元分析进行损伤识别或信号处理技术识别。对海洋平台复杂结构，可借助环境激励及用动态分析技术进行结构实时监测与识别，相关损伤识别方法需要早期信息。

2 振动监测数据分析方法

导管架海洋平台可以运用输入未知条件下的模态参数识别技术从结构的动力响应信号中识别结构的模态参数。利用随机减量法提取结构自由响应信号，时序分析法或复指数提取结构的模态参数，运算量较大但识别精度较高。数据处理方法如下：

2.1 随机减量法

随机减量法是一种提交结构自由衰减响应信号的数据处理处理方法[2-4]，因其具有在工程中应用简单、耗资低廉、效率较高等优势，已广泛应用于结构参数的识别。该方法的核心是假设一个稳定的随机激励系统，其响应是确定性响应和外部负载激励响应的组合。在相同的初始条件下，对响应的时间历程进行分段获取，计算多段获取信号的总体平均值，从而达到提取自由衰减响应的目的。

对于海洋导管架结构系统，某个点在随机激励下的动力响应可表示为[5-6]：

式中：D(t)为结构系统原始位移为 1、原始速度为 0的系统自由振动响应；V(t)为结构系统原始位移为0，原始速度为 1的系统自由振动响应分别为结构系统振动的原始位移和原始速度；h(t)为系统单位脉冲响应函数；f(t)为外部激励。

2.2 ARMA模型时间序列分析方法[3]

该方法是借用参数模型实现对有序随机振动响应的数据进行处理，从而实现模态参数识别的方法。

可以用高阶微分方程来描述 N个自由度的线性系统激励与响应之间的关系。在离散时间域内，可用一系列不同时刻的时间序列表示的差分方程来表示该微分方程，即ARMA时序模型方程：

式中：xt为响应数据序列；2N为自回归模型和滑动平均模型的阶次；ak、bk为待识别的自回归系数和滑动均值系数；ft为白噪声激励。

当 k＝0 时，设 a0＝b0＝1。

2.3 复指数法[4, 7]

复指数法是采用复指数函数和的形式来表示基于结构的自由振动响应或脉冲响应函数，然后通过线性方法确定未知参数。该方法的核心是将振型叠加法与振动微分方程相分离，建立动态响应与模态参数之间的关系。通过拟合脉冲响应函数，可以获得完整的模态参数。

复指数法不依赖于模态参数的初始估计值。优点是将非线性拟合问题转化为线性问题，并且不太需要识别所需的复杂模态参数。缺点是选择正确的模态顺序所用时间较长，并需要做出多个假设来确定正确的模态节数。

一个多自由度的粘滞阻尼线性系统中，q点力所引起p点位移频响函数可以表示为：

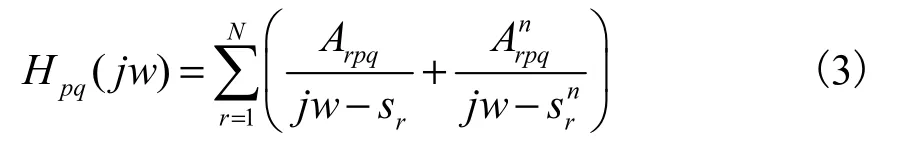
式中：Arpq为第r阶模态相应的留数；J为虚数，取值为为系统的自由度数；sr为频响函数第r阶模态的极点。

3 监测技术适用性验证

3.1 导管架平台应用试验

以东海某导管架平台为监测对象，在其上部组块开展结构振动实时监测工作，监测设备采用的结构振动监测系统是美国 BDI STS-Wifi无线结构测试系统，系统设备包括：基站1台、节点模块4台、传感器16个(见图1)。

图1 BDI STS-Wifi无线结构测试系统Fig.1 BDI STS-Wifi wireless structure test system

根据设计、制造与安装资料和结构服役状态记录资料，建立平台精细有限元模型，对平台进行静力和动力分析，找出了平台在各种环境激励下位移响应最大的位置。选取了16个点位布置了传感器(见图2)。

图2 振动检测布点示意图Fig.2 Vibration detection layout

3.2 基于振动监测数据的结构安全评估

对于老龄导管架平台，由于未进行相应的监测，缺少历史监测数据。针对这种情况，我们具体分析平台结构在服役期间可能出现的损伤工况，通过有限元分析来获取平台结构在不同损伤工况下固有频率的变化规律，将所得数据建立变化分布数据库。然后，将平台实时监测所得数据放入数据库中，通过对比分析得到平台损伤判定结果。

3.2.1 自振频率辨识

将监测所得振动数据经过随机减量法进行预处理，截取常数 A取值为输入数据长度的 1/10左右。经过随机减量法获得的数据如图3所示，图中所输入实验数据为某点的X轴方向振动加速度。

图3 随机减量法输入数据Fig.3 Input data of random decrement

图4 随机减量法预处理数据Fig.4 Preprocessing data of random reduction method

经过预处理后，分别通过 ARMA法和复指数法对模态参数进行识别，要求输出模态阶数的数目 Mj小于截取常数的 1/4，大于截取常数的 1/6，即 A/6＜Mj＜A/4，如果Mj取值过小，则计算数据无法很好的拟合实测数据，造成模态频率的丢失；如果 Mj选取过大，则会无法计算出合适的拟合曲线。一般通过选取不同的输出模态阶数 Mj，然后对输出模态进行筛选[8]。图5、6所示为实测数据与拟合曲线对比图。

图5 复指数法拟合曲线Fig.5 Fitting curve analysis using complex exponential method

图6 ARMA法拟合曲线Fig.6 Fitting curve analysis using ARMA method

从以上拟合曲线图中可以看出复指数法和ARMA法计算得到的拟合曲线跟实测数据有很好的拟合度。

选取平台4个监测点的振动加速度信号，经由随机减量法预处理后经过ARMA法和复指数法得到平台的前阶自振频率，见表1。

在采用复指数法和 ARMA法时，需要给噪声提供出口，这通常就需要提高模型的阶次，有时噪声模态的增加值要大于真实模态的阶数[9]。这时会产生虚假模态。为了删除过程中产生的虚假模态，本文采用两种稳定图法和阻尼删除法相结合的方式，其中稳定图法是通过对比不同模态阶数的计算模型。如果这些模型获得的拟合曲线与从监测数据获得的曲线非常一致，则最稳定和出现次数最多的模态可以被认为是系统的真实模式。阻尼比删除法是分析识别得到的各阶模态阻尼比，通常认为阻尼比小于 1%,或者大于 20%,是虚假模态[8,10]。

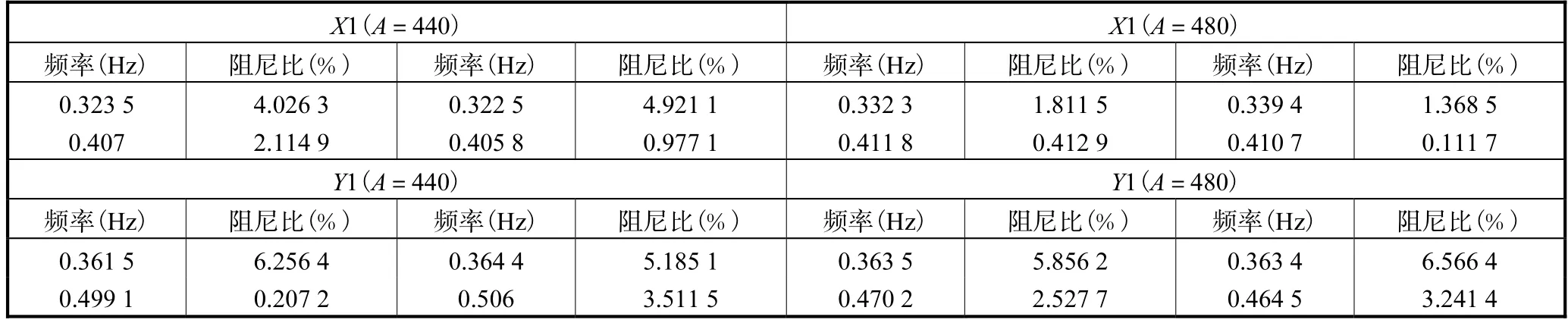
表1 复指数法与ARMA法辨识初始数据Tab.1 The initial data identified by complex exponential method and ARMA method

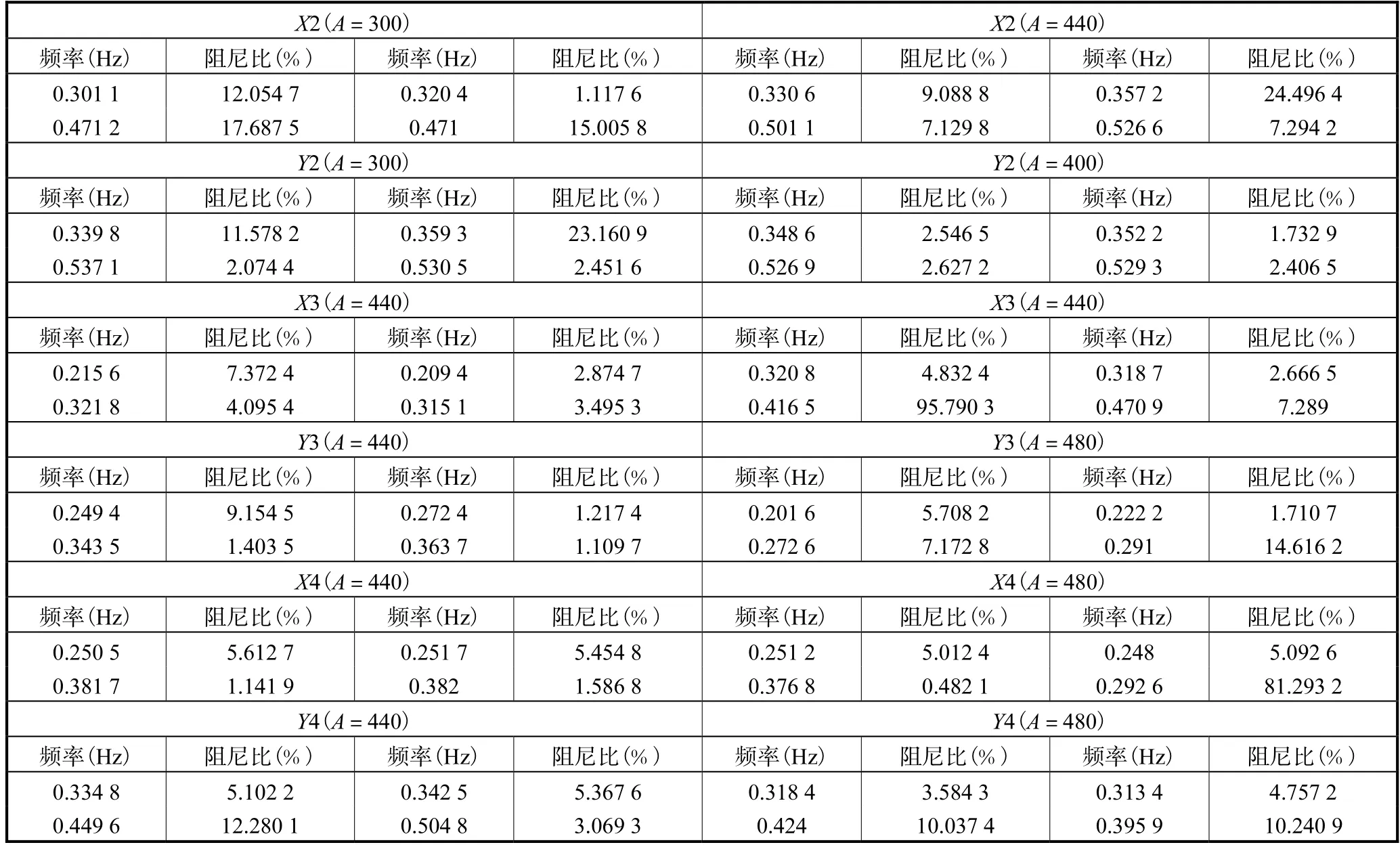
续表1(Continued)

通过表2中模态频率数据进行筛选，得到测点自振频率数据。

表2 最终辨识数据Tab.2 The final identification data

3.2.2 基于有限元分析的安全区域确定

根据平台完工文件、历次改造和检测资料，采用ANSYS有限元分析软件建立了导管架平台结构计算模型(见图7)。

综合考虑平台结构产生损伤的因素，确定平台可能产生损伤的工况，包括平台整体刚度衰减、平台关键结构杆件的失效、平台模块质量增加以及平台结构关键杆件刚度衰减等。然后对上述工况模态分析。

图7 导管架平台ANSYS计算模型Fig.7 Jacket platform ANSYS model

通过模态分析，得到上述工况下平台横摇和纵摇频率值，从而得出平台不同结构状态下的横摇频率以及纵摇频率分布图，如图8所示：

图8 多种工况下平台横摇频率——纵摇频率分布图Fig.8 Jacket platform rolling pitch frequency distribution under different conditions

由分析结果可以看出，平台整体刚度衰减时，横纵摇频率的变化呈线性关系，随着整体刚度的衰减增大横纵摇频率逐渐减小；主桩腿和斜撑失效的点位于刚度衰减线的上方表明杆件失效时纵摇频率变化幅度较横摇小，主桩腿失效与斜撑失效相比横摇减小更大，位于图中左上，斜撑失效位于图中右上；平台上模块质量增加时，频率点大致位于刚度衰减线附近靠下，不同模块质量增加导致位置变动。

3.2.3 平台结构健康状态判定

通过上节中的结构模态分析，得出了平台在完整状态和不同损伤状态下横摇频率和纵摇频率分布图，以此为依据，对比表2中对现场实测数据分析所得的辨识模态参数，可对平台结构的损伤情况进行判定。

将实测数据放入横摇频率和纵摇频率分布图中，如图9所示：

图9 多种工况下平台横摇频率——纵摇频率分布图(加入辨识模态)Fig.9 Jacket platform rolling pitch frequency distribution under different conditions(adding the identification mode)

对上图进行分析，平台完整状态(原设计)下计算所得横摇固有频率要比实测结果偏大约 6.4%,，而纵摇固有频率则偏大约 7.8%,，模态识别的频率大致在刚度衰减线和质量增加线附近靠下。由此说明，该平台结构固有频率的改变可能由于上部整体刚度衰减或平台模块质量改变所引起。同时，根据平台历年维修和改造记录可以发现该平台从服役至今没有进行大的改造，平台质量也没有大的变化，因此，可以排除因平台模块质量增加引起平台固有频率变化的可能，而且平台服役年限已超过 10年，由此可以判定该平台主要发生了整体刚度衰减。

4 结 论

本文将振动检测技术应用到导管架平台结构健康监测中，以某导管架平台结构为试验对象，从振动监测数据分析、导管架平台在不同损伤条件下的模态分析及导管架平台结构健康状态判定等方面开展研究，得到结论如下：

①采用随机减量法对振动监测数据提取的特征函数分别采用ARMA法与复指数法进行模态参数识别，得到的拟合曲线跟实测数据有很好的拟合度。采用稳定图法和阻尼比删除法相结合的方法对 ARMA法与复指数法所得模态频率数据进行筛选，最终可得到平台的实际固有频率。

②通过导管架平台结构的模态分析得到平台不同损伤工况下的动力学参数变化规律，以此为依据，结合经过数据分析所得平台实测辨识模态参数，可以实现对平台损伤模式的判定。

③将平台实测数据放入模态分析所得频率变化分布图中，并结合平台实际情况，判定该平台主要发生了整体刚度衰减。由此验证了振动检测技术在平台结构健康监测上的适用性。