Detection of Magnetic Field Gradient and Single Spin Using Optically Levitated Nano-Particle in Vacuum∗

Ke-Wen Xiao(肖科文),Lei-Ming Zhou(周雷鸣),Zhang-Qi Yin(尹璋琦),and Nan Zhao(赵楠)Beijing Computational Science Research Center,Beijing 00084,China

2Center for Quantum Information,Institute for Interdisciplinary Information Sciences,Tsinghua University,Beijing 100084,China

1 Introduction

The pioneering work of Ashkin and co-workers in 1970s[1−3]has stimulated the investigations of the optical trapping of dielectric objects. Since then,the optical tweezers give rise to enormous research progress in biophysics,[1,4−5]colloidal sciences,[6]micro- fluidic dynamics.[7]When the system is in high vaccum,the optically levitated particle can make quality factor potenitially reach 1012[8−11]and has high position measurement sensitivity due to the untethered feature of this system.[8,12]Therefore it is a promising system for the ground state cooling of the mechanical oscillator[13]and the preparation of the macroscopic quantum state[8,14]and other remarkable investigations.[10,12,15−19]Different material and different scale particle levitated by optical tweezers(OT)[9−10,12]can be applied for searching of non-Newtonian gravity,[20]the detection of gravitational wave[21]and the torsional mode by nonspherical particle.[22−23]

The position measurement of the microparticle trapped by OT has many technologies,for example,total internal reflection microscopy,dynamic light-scattering(DLS)[24]and diffusing wave spectroscopy(DWS).[25−26]Total internal reflection microscopy can achieve 1 nm spatial resolution and up to 1µs temporal resolution.[27]Furthermore,DLS and DWS can have a spatial resolution of sub-nanometers and a temporal resolution on the order of nanoseconds.[26,28−29]However,these techniques can only get ensemble averaged results using these techniques,thus,they cannot be used to measure the instantaneous velocity of a single microscopic particle.[30]For better spatial and temporal resolution,balanced beam detection is brought up and became the standard tool to measure positions of microscopic particles for more and more researches.[31−32]By improving this technology,the spatial resolution and temporal resolution respectively achieve 0.03 nm and 0.01µs,[33]and it prompts the direct observations that the instantaneous velocity of microparticle[12,16]and the full transition from ballistic regime to diffusive Brownian motion[12,16,34]in air or liquid.This technology is very helpful to the detection of the single spin and the gradient of the magnetic field.

Because of the reconfiguration of the OT system,the particle with the single spins trapped by OT is used for the spin-optomechanical hybrid system for investigation.[9]In the usual case,the negatively charged nitrogen-vacancy center(NV−)in diamond is a stable source of single spin or spin ensembles and it has stimulated substantial interest in quantum metrology,[35−36]quantum information,[37−38]the fundamental principle of quantum mechanics[39−40]and nanoscale sensing.[41−42]It displays a long ground-state spin coherence lifetime at room temperature[43]and can be considered as a stable optically accessible qubit in bulk diamond,[44]and has been leveraged to spin reading and writing to nuclei.[45]Nowadays,nanodiamond trapped with ensembles NV center[46]or single defect[47]by OT be used to the detection of the biological magnetic sensing.[48−49]Compared to diamonds,the ferromagnetic material is also a good spin source,which has high spin density,for example,the spin density of yttrium-iron-garnet(YIG)is(2×1022cm−3)[50−51]and is also suitable for the application of the experiment of superconductor quantum bit because its magnetic ordering(Curie)temperature is as high as 559 K.[52]

By utilizing progressive detective technologies of displacement and spin-optomechanical hybrid system,we have proposed a scheme for detecting the single spin and the gradient of magnetic field.In this spin-mechanics hybrid system,a ferromagnatic nano-particle or nanodiamond is trapped by OT,and the collision between the residual air molecules and nano-particle results in the Brownian motion of particle.[16]The temperature and the pressure of the residual air affect the displacement of the particle trapped by OT.At the same time,the spin loading in the nanoparticle also prompts particle to move in the magnetic field gradient.In general,the displacement fluctuation of the particle caused by spin flipping in the magnetic field is overwhelmed caused by molecular collision of the residual air,therefore the effect of the spin is not detected.In order to extract the position signal caused by spin flipping,lowing temperature,increment of the gradient of magnetic field,and spin number are promising methods.Based on these method,the displacement fluctuation ratio caused by spin flipping and environments is introduced.Combining the theoretical analysis and the numerically simulation,the displacement fluctuation caused by spin flipping plays a leading role to the environments when the ratio is larger than unity.Therefore,the gradient of magnetic field single spin can be detected by this spin-optomechanics hybrid system.

This paper is organized as follows.In Sec.2,we introduce the model of this system and deduced the ratio of the particle’s displacement fluctuation caused by spins flipping in the magnetic field gradient and caused by collision between the particle and the residual air molecules.In Sec.3,we present the measurement scheme of the gradient of the magnetic field by utilizing YIG nanoparticle trapped by optical tweezers and verified by numerical simulation and theoretical analysis.In Sec.4,the single spin detection can be realised based on the nanodiamond with NV center trapped by OT and we describe the methods of promoting the displacement fluctuation ratio of the particle caused by spin flipping and collision between nanoparticle and residual air.The conclusion is presented the last section in this paper.

2 Model

An optically trapped nanoparticle in non-perfect vacuum will exhibit Brownian motion due to collisions between the nanoparticle and residual air molecules in their three decoupled translational spatial dimensions.[22]When the spins are loaded into the nanoparticle as shown in Fig.1,according to the Newton’s law,the equation of motion for the optically trapped micro-sphere without feedback cooling in x direction is[17]

where we can use the mass m of particle and the stiffness factor k due to optica√l trap to define the particle’s oscillating frequency Ω0=without no damping.

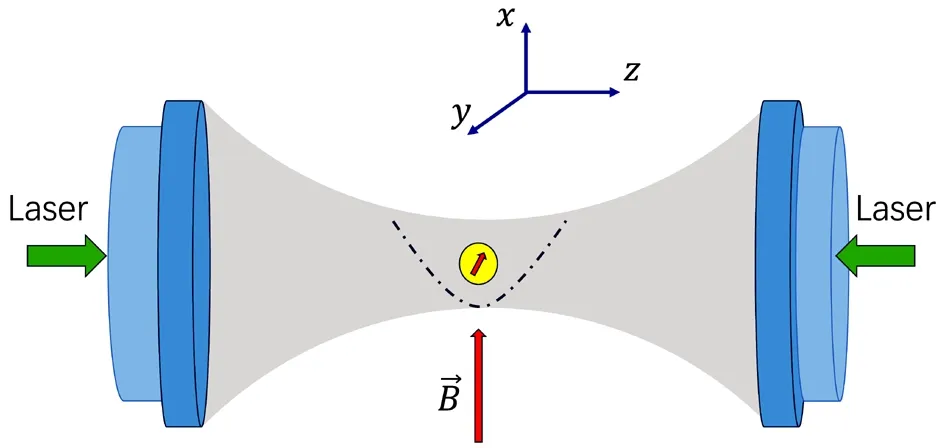
Fig.1 A nanoparticle loaded spins is trapped by lasers and controlled by magnetic field B.The particle stochastically moves in the focal plane,and the direction of magnetic filed is along x direction.

In the experiment,the nanoparticle can be trapped by the strongly foused beam.We can adjust the trapping laser power Pt,the wave length of laser λ and the numerical aperture of the lens NA for trapping nanoparticle. In this paper,Pt= 0.1 W,λ = 1064 nm,and NA=0.8,so we can get the oscillating frequencyfor different material nanoparticles,where c is the light velocity and n is the refractive index of particle.For the damping system,the Stokes friction coefficient due to air molecules is γ,and Ftot=Fmol+Fspin,[50,54]Fmol=is the Brownian stochastic force due to residual air molecules.For convenience,we can set

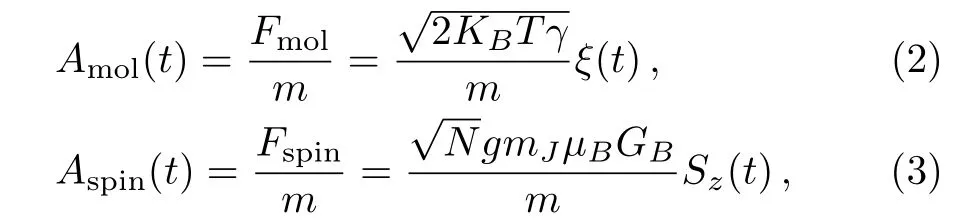
where ξ(t)is a normalized white-noise process,N is the number of spin in nano-particle,g and mJare respectively the electron’s Lande g-factor and magnetic quantum number.µBis Bohr magneton,GBis the gradient of the magnetic field and the direction of GBis parallel to the direciton of B,and Szis the spin loaded in the particle,every spin has two state,up and down.In our paper,we set the up state of spin is 1 and the down state is−1,every spin can be affected by the temperature of the particle,the interaction of spins and other reasons so that the random flipping.Therefore,the relaxation time of spin can be introduced for describing the random process of the spin flipping as follow

where τcis relaxation time.Hence at different times t and t′,the correlation function of acceleration,Amol(t)and Aspin(t),as follow:

where the amplitude of acceleration caused by molecules and spins arerespectively.

The solution of Eq.(1)is:

where the cyclic frequency of the damped oscillator isand Γ depends on temperature and the air pressure of the residual air in the high vacuum from A1.It is obviously that ⟨x(t)⟩=0,δx(t)=x(t)−⟩,so

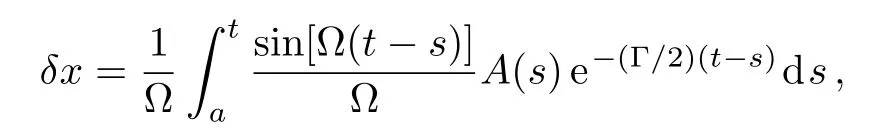
and ⟨δx⟩≡ 0 in the long-time condition.The correlation function of displacement ⟨x(t)x(t+ τ)⟩can be given as follow:

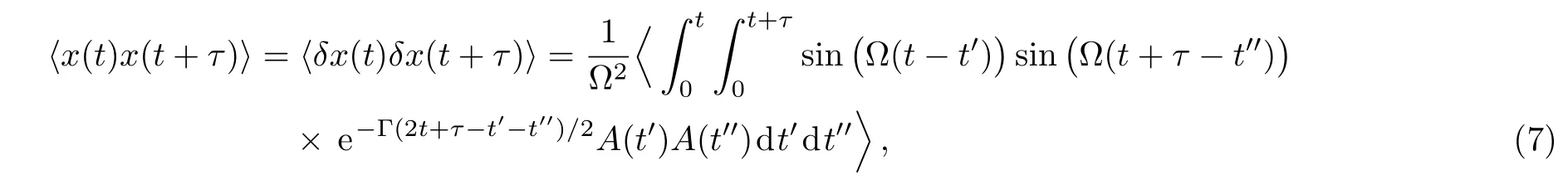
where τ is time interval.When τ approaches zero,this correlation function of displacement presents the variance of displacement.

In Eqs.(6)and(7),A(t)is acceleration resulting from the force of molecules and spins,so the correlation function of displacement⟨x(t)x(t+ τ)⟩can be decomposed into two parts,

where

According Eq.(9),Imol/spinis represented the displacement correlation caused by molecular collision of residual air or by spin flipping in magnetic field.At first,we give the displacements correlation of Imol,

when τ is very short,

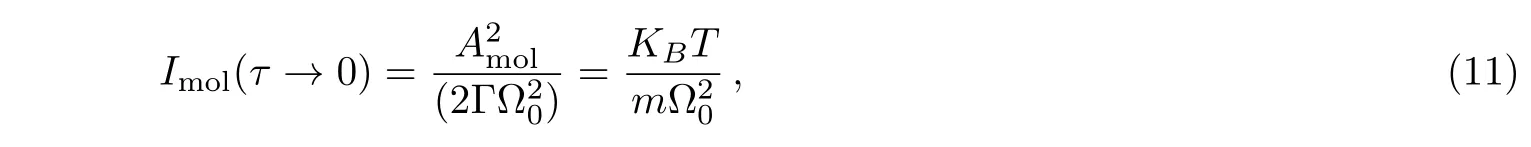
the variance of the displacement only depends on the temperature for the trapped nanoparticle.

On the other hand,for the displacement correlation function caused by spin flipping,Ispinis given

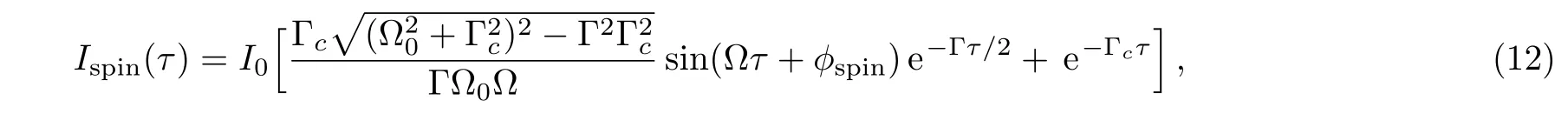
from computation Eq.(9),where

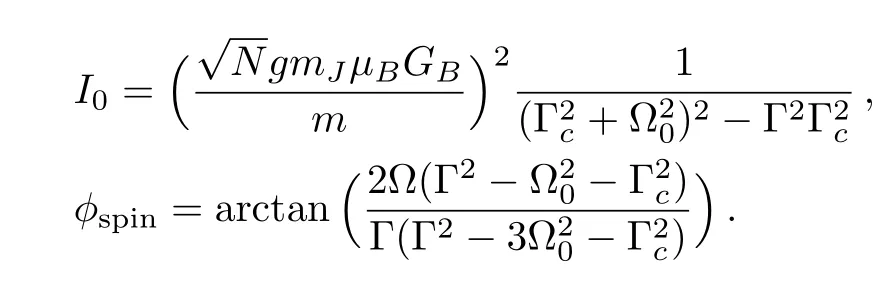
For investigating the variance of the displacement caused by spin flipping,we set τ→ 0,Ispinis simplified to

For comparing displacements caused by molecular collision and spin flipping,κ=Ispin/Imolis proposed as fol-low:

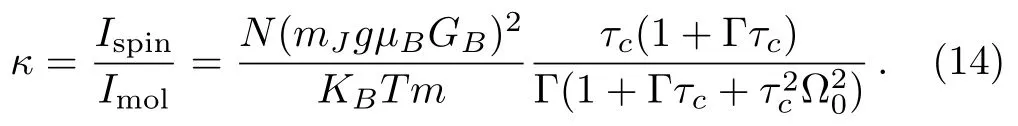
The ratio κ of displacement correlation caused by spins flipping and by moleculardetermines which effect is the dominant role,andis the ratio of the displacement fluctuation of the particle resulting from spin flipping and molecular collision.When ratio is greater than unity,the spins flipping in magnetic field prevail and the signal of the particle’s displacement caused by spin flipping can be detected,on the contrary,signal of the displacement caused by spin flipping is covered up by molecular collision of residual air.From appendix A,Γ is relevant to residual air pressure and temperature in this system.

3 Detection of the Magnetic Field Gradient

The increment of the spin number can enhance the spin signal from Eq.(14),which is beneficial for the detection of the magnetic field gradient.That is because the randomly flipping effect of the spin can become strong after increasing the spin number.In this scheme,we take the YIG nanoparticle for example and consider a YIG nanoparticle trapped by OT and the spin can be affected by magnetic if eld.Because of the ferromagnetism of the particle,we can assume that the spins in YIG can be randomly flipped by the spin relaxation.

In the first case,we take the 100 nm YIG nanoparticle for example and there are 8.85×107spins below the 273 K in particle.These spins flip collectively from one state to another,therefore,the position of the nanoparticle moves from one position to another.Figure 2 shows the flipping of the spin state and the displacement fluctuation resulting from molecular collision and spin flipping.In this case,the standard deviation of the particle’s displacement caused by molecular collision of residual air(∆air)is 0.40 nm and GB=10 kT/m.The standard deviation of the particle’s displacement caused by spin flipping in magnetic field(∆B)is 1.03 nm.κ1/2is 2.58,the collective effect of the spin can be detective.From our simulation,the position of the particle changes synchronously with the spinflipping in Fig.2(a).The inset of Fig.2(a)shows the harmonic oscillation of the particle when the spins do not flip.In this simulation,the simulating time is 100 ms and simulating time-step is 1µs.By numerically simulating,we can obtain a series of sampling points,and every sampling point corresponds different displacement of nano-particle at different time.For any sampling point,we can get the nano-particle’s displacement and count the number of occurrences of any displacement.Base on this result,we can get the Fig.2(b).In this case,we assume that all spins of the nanoparticle flip at the same time from the same state to another.However,in the realistic case all the spins ensembles do not collectively flip from one state to another at the same time.Therefore the displacement fluctuation caused by spin flipping in magnetic field gradient should be investigated anew.

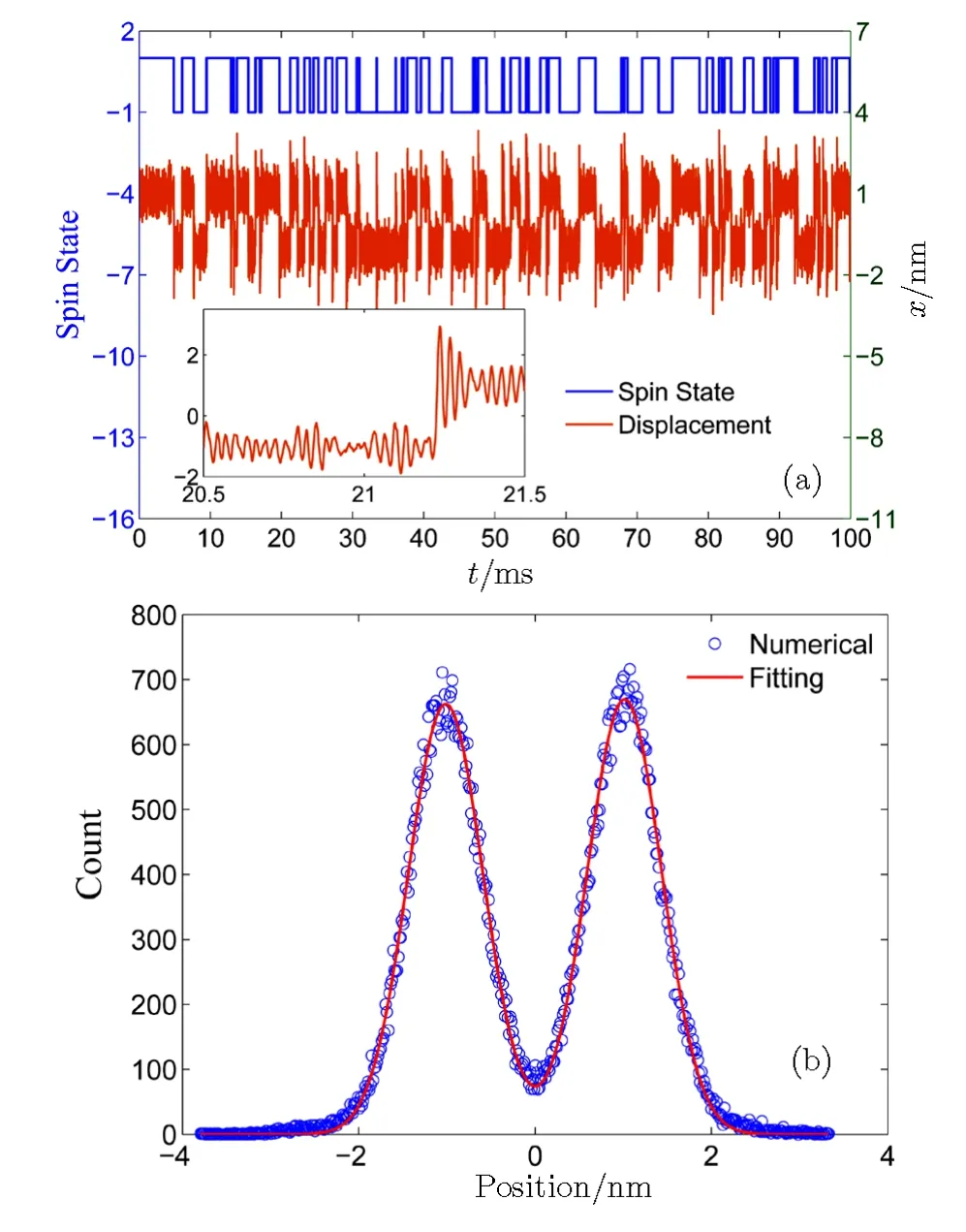
Fig.2 (Color online)The spin of the YIG nanoparticle collectively randomly flips and the position synchronously changes with spin state,and the position of the YIG particle is statistically analysed.(a)shows the every spin of YIG nanoparticle has the same property of flipping and the flipping time is random,however,the mean flipping time is determined,1 ms(blue curve).The yellow curve corresponds to the changing of the position of the particle.(b)The statistics of the position of the particle and its fitting.The radius of this YIG particle is 100 nm and the temperature and the residual air pressure are respectively 10 mK and 10 Pa.The gradient of magnetic field is 104T/m.The refractive index of YIG is 2.2.

In the realistic case,the displacement fluctuation caused by molecular collision of residual air is not changed for the determined environment,but the displacement fluctuation caused by spin flipping in magnetic field is relevant to the equivalent spin number in YIG.Every spin flipping is random,therefore,the equivalent number of spin up and spin down is random and less than 8.85×107below the 273 K.The effect of displacement fluctuation caused by spin flipping is so week that cannot be detected compared to previous case.In addition,the position distribution of particle can be detected as a Gaussian distribution and is not similar to two peaks distribution in Fig.2.For distinguishing the displacement fluctuation caused by molecular collision and by spin flipping,at first,we can theoretically and numerically compute the displacement fluctuation caused by the residual air molecular collision,and then numerically compute the total displacement fluctuation,at last,the displacement fluctuation caused by spin flipping can be got from the difference between the total displacement fluctuation and the displacement fluctuation caused by molecular collision.For increasing the displacement fluctuation caused by spin flipping in magnetic field,we can increase the gradient of the magnetic field,GB.

For the 100 nm YIG nanopartice,the state of the spin ensembles are Fig.3.This particle contains many spins and every spin flips randomly,therefore,the particle will randomly move in the focal plane. The oscillatory displacement of particle is determined by the gradient of magnetic field and the environments.When the temperature and the residual air pressure are respectively 1 mK and 1000 Pa,∆airand∆Bare respectively 0.18 nm and 2.0 nm by the statistical computation under GB=10 kT/m.These are depicted in Fig.3.

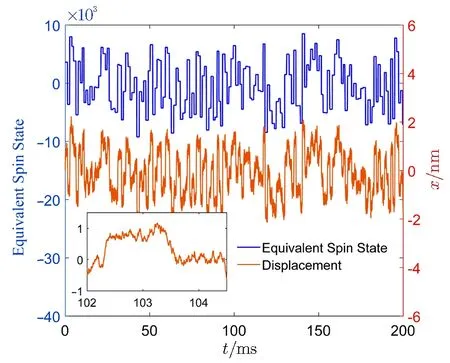
Fig.3 (Color online)The synchronously oscillation of the nanoparticle with the flipping of the spins ensemble.The blue curve is the state flipping of the spin ensembles of the YIG nanoparitcle.The yellow curve shows the changing of the position change of the particle.The inset is the oscillation of the particle in the short time.The radius of this YIG particle is 100 nm and the temperature and the residual air pressure are respectively 1 mK and 1 kPa.The gradient of magnetic field is 104T/m and the refractive index of YIG is 2.2.

On the contrary,if we have statistically computed the displacement fluctuation caused by spin flipping in the magnetic field,the gradient of the magnetic field can be got.Different gradient of magnetic field can stimulate different displacement fluctuation,therefore,the correspondence between the displacement fluctuation and the gradient of magnetic field can be depicted.For this system,when the magnetic field does not exist,the particle’s displacement fluctuation only results from the molecular collision of residual air.The fluctuation of the displacement caused by residual air molecular is constant.However,when the magnetic field exists,the displacement of the particle can be very larger than the thermal fluctuation of the particle.In this case,we can give the relation between displacement fluctuation of the particle and the gradient of magnetic field GBlike Fig.4.When GBis very small,∆Bis not much bigger than∆air.However,when GBincreases to 104T/m,∆Band∆aircan be distinguished significantly.The larger gradient of the magnetic field will result in the bigger position fluctuation.Considering the determined environment,∆airis not changed and we can know that∆Bcan be detected when GB≥1 kT/m.There are three styles line derived from simulation, fitting and analysis.From Eq.(14),the sensitivity to the gradient of the magnetic field is determined by

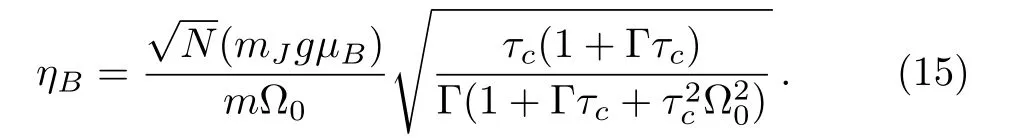
The sensitivity has positive correlation with the spin number.When a 100 nm YIG nanoparticle trapped by OT,the position detective technology and statistical method can give different magnetic field gradient,and the results from numerical simulation and theoretical analysis can match well.In Fig.4,the fitting result of sensitivity is 1.67×10−13m/T(the dashed curve)and the analysis result is 1.95× 10−13m/T(the “+”symbol).They can match better each other in a longer time statistics.The inset figure(a)depicts that the displacement caused by magnetic field can be detected until GB≥103T/m,even though the displacement caused by GBis smaller than the displacement caused by residual airs.

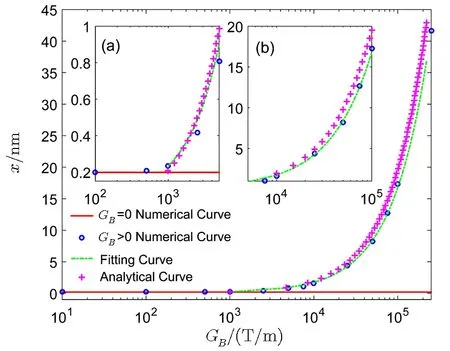
Fig.4 The relationship between displacement fluctuation of particle and the graident of the magnetic field in the environment of the temperature(1 mK)and the air pressure(1 kPa).The inset(a)is the smaller gradient of the magnetic field and the inset(b)is the larger gradient of the magnetic field.The the circle,dashed line and‘+′line are respectively simulating results, fitting results and the analytical results.The refractive index of YIG is 2.2.

4 The Detection of the Single Spin

A nanodiamond containing an NV center have one spin,it also can be trapped by OT.[9]In the theoretical analysis,we can get the ratio of standard deviation between xspinand xmol,the particle’s displacement can be also simulated at the same time.The position of the particle oscillates synchronously following the flipping of the spin in the NV center of the particle like Fig.5(a).The spin state flips between state−1 and state 1,and the particle synchronously oscillates in the region between−10 nm and 10 nm.

Fig.5 The synchronous oscillation of the nanoparticle with the flipping of the single spin and the statistical and fitting results about the distribution of the particle’s position.(a)The blue curve is the spin state in the nanoparitcle with NV center.The yellow curve shows the changing of the position of the particle.The inset is the oscillation of the particle in the short time.(b)The statistical and fitting results about the distribution of the particle’s position. ∆Band ∆airare respectively the displacement of the particle caused by the magnetic field and the residual air.The radius of this nanodiamond particle is 30 nm which contains only one spin,and the temperature and the residual air pressure are respectively 1 mK and 0.5 Pa.The gradient of magnetic if eld is 106T/m.

By utilizing the statistical and fitting methods,we can give the statistical property of the particle’s position caused by molecular collision of residual air and the spinflipping of magnetic field.In proper coefficients,there are two most probable positions of particle in the focal plane,which can be detected by detector of the position.This represents the particle oscillates randomly between two positions.The width of the position peak of particle results from the collision between the particle and the residual air molecules.Figure 5(b)is the statistical and fitting results.In this case,∆Band∆airare respectively 3.44 nm and 2.38 nm,which match well with the theoretical results 3.49 nm and 2.25 nm from Eqs.(11)and(13).It is easy to distinguish the displacement fluctuation caused by molecular collision and by single spin flipping,the single spin can be detected.

The statistical method shows two maximum counts of detector about the position of the particle. These maximums represent that the particle prefers staying the greater probability positions to the other position.These maximum positions are just caused by spin flipping from one state to another in the magnetic field.At the same time,if the spin stays in one state and the nanoparticle is collided by the residual air,therefore,the nanoparticle has the property of the Brownian motion near the maximum position.

In the last example,the ratio κ1/2is 1.5,although it is enough for distinguishing the effect between magnetic field and the residual air,we can get more significant effect of the magnetic field about the particle position by adjusting other coefficients.Hence,it is necessary to know the property of κ about the trapping frequency(Ω0),the relaxation time of spin(τc)and so on.

In order to discuss the problem,we set:

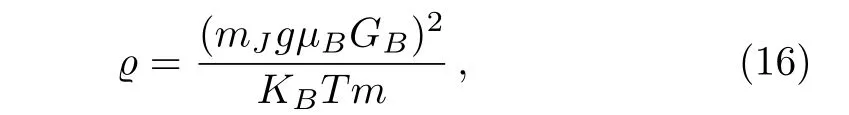
for Eq.(14).ϱ is independent of the coefficients of the trapping lasers which determines the trapping frequency,Ω0.Therefore,the investigation about the relationship between κ and Ω0is our first subject.

4.1 Ω0-dependence

From Eq.(14),κ is monotonous decreasing function when increasing Ω0,and ∂κ/∂Ω0is as follow:

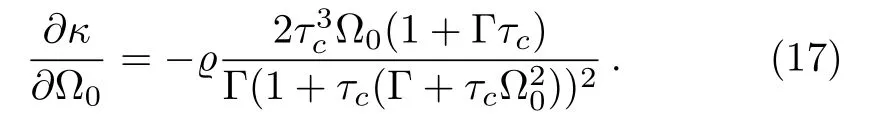
Equation(17)is eternity negative for Γ >0 and τc>0.This presents κ decreasing with increasing of Ω0for fixed

Although κ declines with the trapping frequency Ω0,different relaxation time of spin also affects the displacement of the particle caused by the gradientthe magneticFig.6.From this figurehe decreasing function with Ω0which matches with Eq.(17).However,under normal case,the trapping frequency must be larger than 80 kHz otherwise the particle would not be trapped for the 30 nm radius of particle.Therefore,the inset of this figure shows the range of the trapping frequency 80 kHz to 160 kHz.It is obvious that the longer the relaxation time of spin is,the more significant the displacement fluctuation of√ spin flipping in the magnetic field gradient is.Althoughis slightly more than 1,we can increase τcin order to increase displacement fluctuation caused by spin flipping by some method.[56−57]Nevertheless,when the trapping frequency is larger, is not sensitive to τc.This property can be verified by analysis of the relationship between κ and τc.

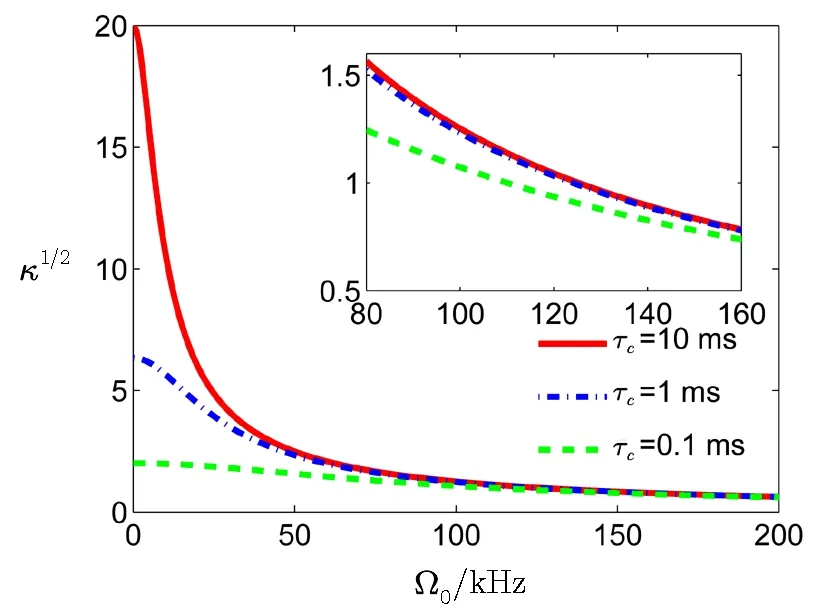
Fig.6 The relation between and Ωabout different0 τc.In this case,the radius of the nanodiamond particle is R=30 nm,the temperature is 1 mK,the residue air pres√sure is P=10 Pa.Different curves represent different with different τc.The units of inset is the same with main figure.

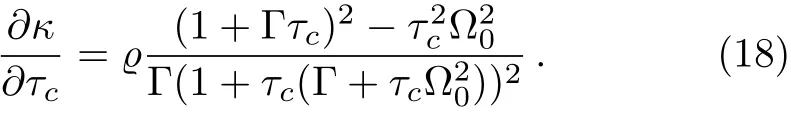
Equation(18)shows that κ has two critical points, τc0=−1/(Ω0+Γ)and τc0=1/(Ω0−Γ),which give some interesting characters for our investigation.In one case,when the system is under-damping,Ω0> Γ,and the space of τcis divided into two range,i.e.τc∈ (0,1/(Ω0−Γ))and τc∈ (1/(Ω0− Γ),+∞).They correspond to ∂κ/∂τc>0 and ∂κ/∂τc<0,respectively.In this case, κ increases with the increment of τcuntil τc=1/(Ω0− Γ)and when τc>1/(Ω0−Γ),κ will decrease.

In another case,when the system is over-damping,Ω0< Γ,κ increases with the increment of τc.The longer the relaxation time of the spin is,the more obvious the effect of spin is.By analysis the second order derivative of κ about τc,

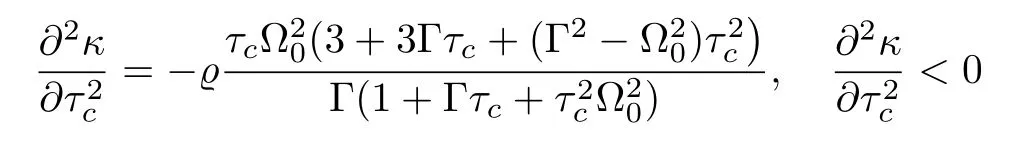
4.2 τc-dependence

The relaxation time of spin can affect the ratio between Ispinand Imolas well.The derivative of κ with respect to τcis always stands up for the over-damping case.These two case can be corresponded with Fig.7.√This figure intuitively shows that the relation betweenκ and τc.For the under-damping case,Ω0=0.25Γ,this trapping frequency is general case,Ω0=98 kHz.That is over-damping,κ has a maximum value when τcis very short.Therefore the relaxation time is not as√ longer as better.However,for the under-damping case,κ increases with the increment of τclike the dashed line in Fig.7,hence the larger displacement of particle caused by magnetic field can be got by adjusting the relaxation of the spin.

Fig.7 The relation betweenand τabout differentcΩ0.In this case,the radius of the nanodiamond particle is R=30 nm,the temperature is 1 mK,the residue air pressure is P=10 Pa.

4.3 Environment Damping

In real system,environmental temperature and the residual air pressure will affect the damping coefficient Γ from Appendix A,and then affect the ratio,κ.Therefore,for convenience,we investigate straightforwardly the relationship between κ and Γ. ∂κ/∂Γ clearly shows that κ decreases with the increment of the Γ as follow:

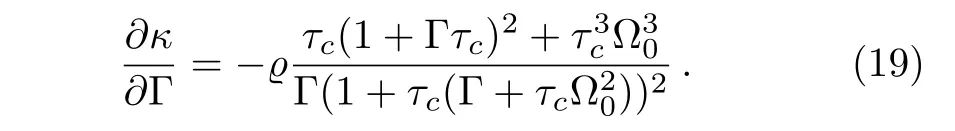
Because ∂κ/∂Γ is always negative for the arbitrary parameters.For getting more remarkable displacement of the particle caused by spin flipping,we can reduce the temperature and the air pressure of the residual air.That is because the reduction of the temperature is equivalent to reduction of the fluctuation of thermal displacement of the particle and strengthening the effect of the spin flipping.The reduction of the air pressure will reduce the friction of the particle with the residual air molecules,the motion of the particle is more obvious.Although,the reducing residual air pressure can strength the signal of the spin flipping,the damping γradresulting from the photon shot noise will be primary and damping Γ from the interaction with residual air can be neglected at very low air pressure.In this case,we can introduce feedback cooling in order to solve this problem.Fortunately,ultrahigh vacuum(P ∼ 10−8mbar)is not strictly demanded in our system,therefore,γradis neglectly smaller than the damping Γ by computation from Ref.[11]so that shot noise is unnecessarily considered.

5 Conclusion

In this paper,we have systematically investigated the motion of the nano-particle loading spins trapped by the optical tweezers in the high vacuum environment.Based on this system,the theoretical analysis has been utilized to study the displacement of the particle caused by molecular collision of the residual air and by spin flipping under the gradient of magnetic field,as well as their ratio.This theoretical analysis inspires a series of proposal about the detection of the gradient of the magnetic field and the detection of the single spin.By utilizing theoretical analysis and the numerical simulation,we present and verify the scheme of the detection of the gradient of the magnetic by trapping YIG nanoparticle.Similarly,this system also can be applied for detection of the single spin by trapping the diamond nanoparticle with NV center.By regulating the parameters,we can make the displacement fluctuation of the particle caused by the spin flipping in magnetic field gradient more remarkable.At last,we present the method about increasing the displacement fluctuation resulting from spin flipping,such as reducing the trapping frequency,increasing the relaxation time of the spin and reducing the temperature and residual air.This spin-mechanics hybrid system with spin have provided a novel experiment platform for high sensitive measurement,macro-ground state cooling etc.

Appendix A:The Damping Factor in the High Vacuum

In the high and ultrahigh vacuum,the damping factor,Γ,can be calculated,[10,58]

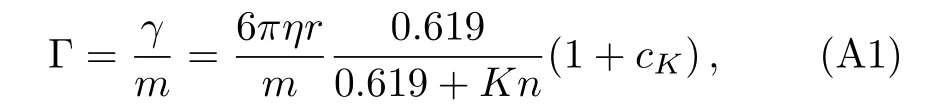
where η =18.52 × 10−6Pa ·s is the viscosity coefficient of air in room temperature and atmospheric pressure,r is the radius of the particle,Kn=s/r is the Knudsen number with s being the mean the free path of air molecules,and cK=0.31Kn/(0.758+1.152Kn+Kn2).The mean free path is

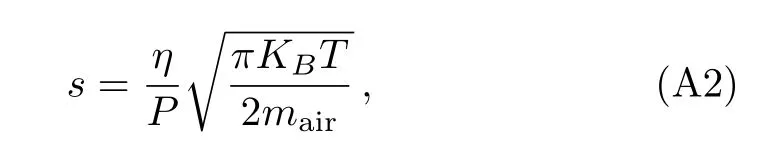
here P is the residual air pressure and mairis the mass of the single air molecule,the value is mair=4.80×10−26kg.

Acknowledgement

We thank Professor Renbao Liu for inspiring discussions.

[1]A.Ashkin,Phys.Rev.Lett.24(1970)156.

[2]A.Ashkin and J.M.Dziedzic,Appl.Phys.Lett.19(1971)283.

[3]A.Ashkin and J.M.Dziedzic,Appl.Phys.Lett.28(1976)333.

[4]A.Ashkin,J.M.Dziedzic,and T.Yamane,Nature(London)330(1987)769.

[5]A.Ashkin and J.Dziedzic,Science 235(1987)1517.

[6]K.Dholakia and P.Zemánek,Rev.Mod.Phys.82(2010)1767.

[7]K.Dholakia,Chemical Society Reviews 37(2008)42.

[8]Z.Q.Yin,A.A.Geraci,and T.Li,Int.J.Mod.Phys.B 27(2013)1330018.

[9]L.P.Neukirch,E.V.Haartman,J.M.Rosenholm,and A.N.Vamivakas,Nature Photonics 9(2015)653.

[10]T.Li,S.Kheifets,and M.G.Raizen,Nature Physics 7(2011)527.

[11]V.Jain,J.Gieseler,C.Moritz,C.Dellago,et al.,Phys.Rev.Lett.116(2016)243601.

[12]T.Li,S.Kheifets,D.Medellin,and M.G.Raizen,Science 328(2010)1673.

[13]P.Rabl,P.Cappellaro,M.V.G.Dutt,et al.,Phys.Rev.B 79(2009)041302.

[14]D.E.Chang,C.A.Regal,S.B.Papp,et al.,Proceedings of the National Academy of Sciences of the United States of America 107(2010)1005.

[15]O.Romero-Isart,A.C.P flanzer,F.Blaser,et al.,Phys.Rev.Lett.107(2011)020405.

[16]S.Kheifets,A.Simha,K.Melin,et al.,Science 343(2014)1493.

[17]J.Gieseler,B.M.Deutsch,R.Quidant,and L.Novotny,Phys.Rev.Lett.109(2012)103603.

[18]J.Gieseler,R.Quidant,C.Dellago,and L.Novotny,Nature Nanotechnol.9(2014)358.

[19]J.Bateman,S.Nimmrichter,K.Hornberger,and H.Ulbricht,Nature Commun.5(2014)4788.

[20]A.A.Geraci,S.B.Papp,and J.Kitching,Phys.Rev.Lett.105(2010)101101.

[21]A.Arvanitaki and A.A.Geraci,Phys.Rev.Lett.110(2013)071105.

[22]T.M.Hoang,Y.Ma,J.Ahn,et al.,Phys.Rev.Lett.117(2016)123604.

[23]K.W.Xiao,N.Zhao,and Z.Q.Yin,Phys.Rev.A 96(2017)013837.

[24]B.Berne and R.Pecora,Tanpakushitsu Kakusan Koso Protein Nucleic Acid Enzyme 49(1976)1676.

[25]G.Maret,et al.,Zeit.Für Phys.B Con.Matt.65(1987)409.

[26]D.J.Pine,D.A.Weitz,P.M.Chaikin,and E.Herbolzheimer,Phys.Rev.Lett.60(1988)1134.

[27]L.Liu,A.Woolf,A.W.Rodriguez,and F.Capasso,Proceedings of the National Academy of Sciences of the United States of America 111(2014)E5609.

[28]P.Zakharov,F.Cardinaux,and F.Scheffold,Phys.Rev.E 73(2006)011413.

[29]J.X.Zhu,D.J.Durian,J.Müller,et al.,Phys.Rev.Lett.68(1992)2559.

[30]J.Mo,J.Chem.Phys.49(2015)5158.

[31]B.Luki´c,S.Jeney,C.Tischer,et al.,Phys.Rev.Lett.95(2005)160601.

[32]T.Franosch,M.Grimm,M.Belushkin,et al.,Nature(London)478(2011)85.

[33]P.N.Pusey,Science 332(2011)802.

[34]R.Huang,I.Chavez,K.M.Taute,et al.,Nature Phys.7(2011)439.

[35]P.Kumar and M.Bhattacharya,Opt.Express 25(2017)719568.

[36]N.Zhao and Z.Q.Yin,Phys.Rev.A 90(2014)042118.

[37]J.Wrachtrup and F.Jelezko,J.Phys.Condens.Matter 18(2006)S807.

[38]P.Neumann,R.Kolesov,B.Naydenov,et al.,Nature Phys.6(2010)249.

[39]Z.Yin and T.Li,Contemp.Phys.58(2017)1.

[40]G.Anetsberger,P.Verlot,E.Gavartin,et al.,Nature Nanotechnol.4(2009)820.

[41]J.R.Maze,P.L.Stanwix,J.S.Hodges,et al.,Nature(London)455(2008)644.

[42]H.J.Mamin,M.Kim,M.H.Sherwood,et al.,Science 339(2013)557.

[43]P.L.Stanwix,L.M.Pham,J.R.Maze,et al.,Phys.Rev.B 82(2010)201201.

[44]F.Jelezko,T.Gaebel,I.Popa,et al.,Phys.Rev.Lett.93(2004)130501.

[45]P.C.Maurer,G.Kucsko,C.Latta,et al.,Science 336(2012)1283.

[46]V.R.Horowitz,B.J.Alemán,D.J.Christle,et al.,Proce.National Acad.Sci.109(2012)13493.

[47]M.Geiselmann,M.L.Juan,J.Renger,et al.,Nature Nanotechnol.8(2013)175.

[48]A.W.Schell,P.Engel,and O.Benson,arXiv:1303.0814(2013).

[49]R.Beams,D.Smith,T.W.Johnson,et al.,Nano Lett.13(2013)3807.

[50]H.Huebl,C.W.Zollitsch,J.Lotze,et al.,Phys.Rev.Lett.111(2013)127003.

[51]M.A.Gilleo and S.Geller,Phys.Rev.110(1958)73.

[52]D.Zhang,X.M.Wang,T.F.Li,et al.,npj Quantum Inform.1(2015)15014.

[53]O.Romero-Isart,A.C.Panzer,M.L.Juan,et al.,Phys.Rev.A 83(2011)013803.

[54]M.G.Raizen,R.J.Thompson,R.J.Brecha,et al.,Phys.Rev.Lett.63(1989)240.

[55]F.Bloch,Phys.Rev.70(1946)460.

[56]G.Q.Liu,Q.Q.Jiang,Y.C.Chang,et al.,Nanoscale 6(2014)10134.

[57]J.Du,X.Rong,N.Zhao,et al.,Nature(London)461(2009)1265.

[58]S.A.Beresnev,V.G.Chernyak,and G.A.Fomyagin,J.Fluid Mech.219(1990)405.