A Numerical Investigation of 3D MHD Rotating Flow with Binary Chemical Reaction,Activation Energy and Non-Fourier Heat Flux∗
2018-07-09DianChenLuRamzanBilalJaeDongChungandUmerFarooq5DepartmentofMathematicsFacultyofScienceJiangsuUniversityZhenjiang220China
Dian-Chen Lu,M.Ramzan,M.Bilal,Jae Dong Chung,and Umer Farooq,5Department of Mathematics,Faculty of Science,Jiangsu University,Zhenjiang 220,China
2Department of Computer Science,Bahria University,Islamabad Campus,Islamabad 44000,Pakistan
3Department of Mathematics,Faculty of Computing,Capital University of Science and Technology,Islamabad,Pakistan
4Department of Mechanical Engineering,Sejong University,Seoul 143-747,Korea
5Department of Mathematics,COMSATS Institute of Information Technology,Park road,Tarlai Kalan,Islamabad 45550,Pakistan
1 Introduction
The subject of non-Newtonian fluid mechanics has been an inspiring and defying area as it enfolds abundant vital problems from petroleum,biomedical food processing,chemical and polymer industries.Non-Newtonian fluid models are quite effective to illustrate the flow of commonly used various fluids available naturally or in processed form like motor oils,polymeric liquids,slurries,biological fluids and pastes etc.Elastico viscous fluid is a kind of non-Newtonian material in which the fluid’s deformity rate decreases once the shear stress is removed.This action is recognized as stress relaxation.In absence of sheer stress the time consumed by the fluid,to regain its equilibrium position due to its elastic characteristics,is named as relaxation time.Upper-convected Maxwell(UCM) fluid model is one of the commonly used elastico viscous fluid models.Maxwell fluid model has gained special attention of researchers in the recent past.Han et al.[1]studied analytical solution of UCM fluid flow past a stretched surface with Cattaneo-Christov heat flux and slip boundary condition.Mustafa[2]found numerical and analytical solution of non-Fourier heat flux in a rotating flow of Maxwell fluid.Ramzan et al.[3]discussed numerical solution of 3D UCM fluid flow with effects of nonlinear radiative heat flux and chemical reaction in attendance of double diffusion.Ramzan et al.[4]also examined three-dimensional UMC magnetohydrodynamic fluid flow with impact of homogeneous-heterogeneous reactions and non-Fourier heat flux with convective boundary conditions.Mustafa et al.[5]analytically investigated the flow of Upper-convected Maxwell fluid and temperature reliant thermal conductivity with Cattaneo-Christov heat flux.Khan et al.[6]found series solution of Maxwell fluid flow with homogeneous-heterogeneous reactions in attendance of heat generation/absorption and chemical reaction. Khan et al.[7]deliberated flow of Maxwell fluid with effects of mixed convection past an oscillating vertical plate using Laplace transform method.Hsiao[8]inspected Maxwell fluid flow past a high efficiency extrusion sheet with electrical MHD,mixed convection and thermal radiation.Hayat et al.[9])cogitated the 3D rotating flow of Maxwell nanofluid with using Optimal Homotopy analysis method.Jusoh et al.[10]found numerical solution of MHD 3D Maxwell fluid flow through a porous stretching/shrinking surface with convective boundary condition.Some more investigations highlighting flow of Maxwell fluid may be seen at Refs.[11–13].
In many engineering processes,like thermal insulation,vaporization,food processing,diffusion of nutrients in tissues,distillation of alcohol,condensation in mixtures,im-portance of mass transfer can not be denied.A valuable contribution of mass transfer may also be found in livingmatter processes including sweating,respiration and nutrition etc.There have been studies in the past highlighting role of chemical reaction in mass transfer processes(see Refs.[14–16]and reference there in)and has a variety of applications like thermal oil recovery,chemical engineering,nuclear reactor cooling,and geothermal reservoirs.Study of binary chemical reaction in the flow of boundary layer was coined by Bestman.[17]He studied the flow of heat and mass transfer past a permeable medium with effects of binary reaction and arrhenius activation energy.Activation energy has a key role in all chemical reactions.It is the minimum amount of energy required for atoms and molecules to be in a position where a chemical reaction may trigger.The idea of activation energy is widely applicable in many fields including oil emulsions,oil reservoir,and mechanics of water.Makinde et al.[18]found numerical solution of time dependent flow with radiation,chemical reaction and Arrhenius activation energy effects past a permeable plate.Later,Maleque[19]talked about solution of time dependent fluid flow in attendance of heat generation/absorption,viscous dissipation,Arrhenius activation energy,and chemical reaction.Awad et al.[20]used the Spectral Relaxation Method(SRM)to find solution of a rotating viscous fluid with chemical reaction and Arrhenius activation energy.Some recent studies featuring both chemical reaction and activation energy are referred at Refs.[21–22].
A reasonable number of applications emphasizing the role of steady and unsteady rotating flows may be found in chemical and geophysical fluid mechanics.These all of applied nature like in thermal power generating systems,in food processing,in the skins of high speed air crafts and in rotor stator systems.The pioneering work highlighting rotating flow was done by Wang.[23]This was followed by a study by Rajeswari and Nath[24]who explored the rotating time dependent flow.Takhar et al.[25]later discussed the effects of magnetohydrodynamic in a rotating flow.Kumari et al.[26]found numerical solution of rotating flow of Power law fluid model using Keller Box method.Zaimi et al.[27]also applied same numerical technique to examine the rotating flow of viscoelastic fluid.Javed et al.[28]investigated rotating fluid flow past an exponential stretched surface.Mustafa[29]deliberated rotating flow of UCM fluid with non-Fourier heat flux.Turkyilmazoglu[30]applied Spectral numerical integration method to find solution of a shrinking rotating disk with effect of magnetohydrodynamic.Recent attempts emphasizing rotating flow are referred at Refs.[31–33].
It is observed that past investigations have not considered the onset of binary chemical reaction and energy activation on 3D rotating flow of Maxwell fluid accompanying non-Fourier heat flux.The present effort is to fill in such gap.Additionally, flow analysis is performed in the presence of magnetohydrodynamic and,heat and mass convective boundary conditions.Novelty of the existing exploration is through the subsequent characteristics.First,we have considered the three dimensional Maxwell rotating fluid flow with chemical reaction and activation energy.Second,the effect of magnetohydrodynamics is considered in the formulation of the problem.Third,we have analyzed the whole scenario in attendance of heat and mass boundary conditions.Fourth,the problem is studied in the presence of non-Fourier heat flux.Fifth,we have found the numerical solution[34−35]using bvp-4c function in MATLAB.Graphical illustrations accentuating effects of arising parameters on all involved fields are presented and well argued.A comparison to a previously published study is also added to validate our results.
2 Mathematical Formulation
Consider a 3D Maxwell rotating incompressible fluid flow(rotating with a constant angular velocity Ω)past an elastic stretched surface placed in the xy-plane in which fluid is positioned at z≥0.The sheet is stretched with a linear velocity uw(x)=ax in x-direction.Let Twand Cwbe the temperature and concentration at the surface.However,T∞and C∞are the temperature and concentration far away from the surface as shown in Fig.1.

Fig.1 Geometry of the Problem.
A magnetic force of strength B0is applied normal to the plane of the stretched surface.Taking into account the binary chemical reaction with activation energy[20]and non-Fourier heat flux,[36]the governing equations of 3D Maxwell rotating fluid are given by:
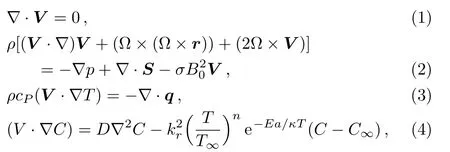
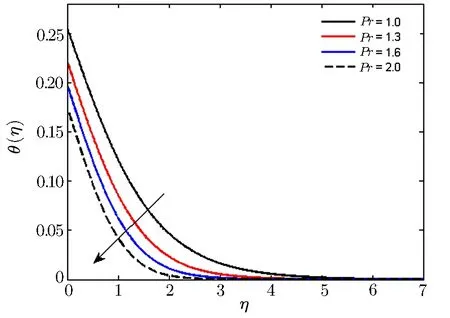
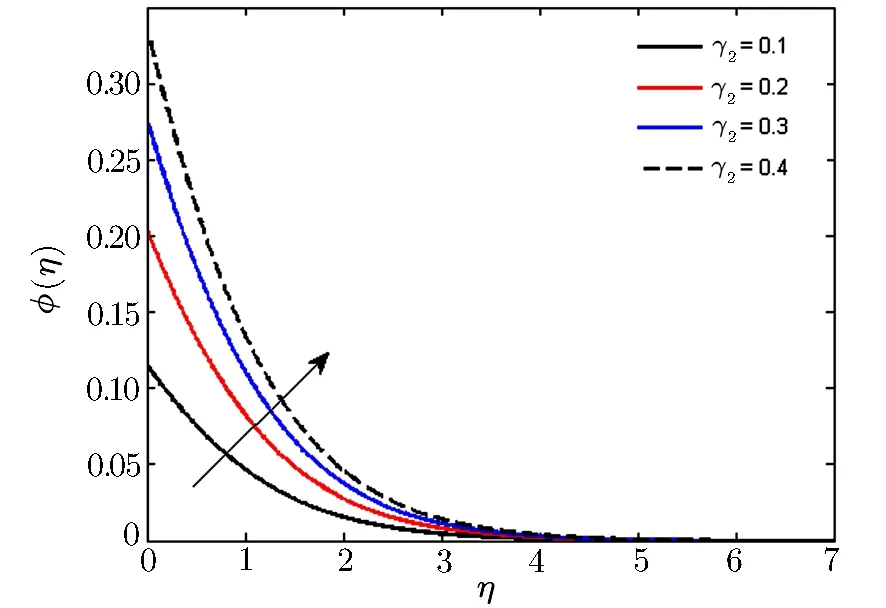
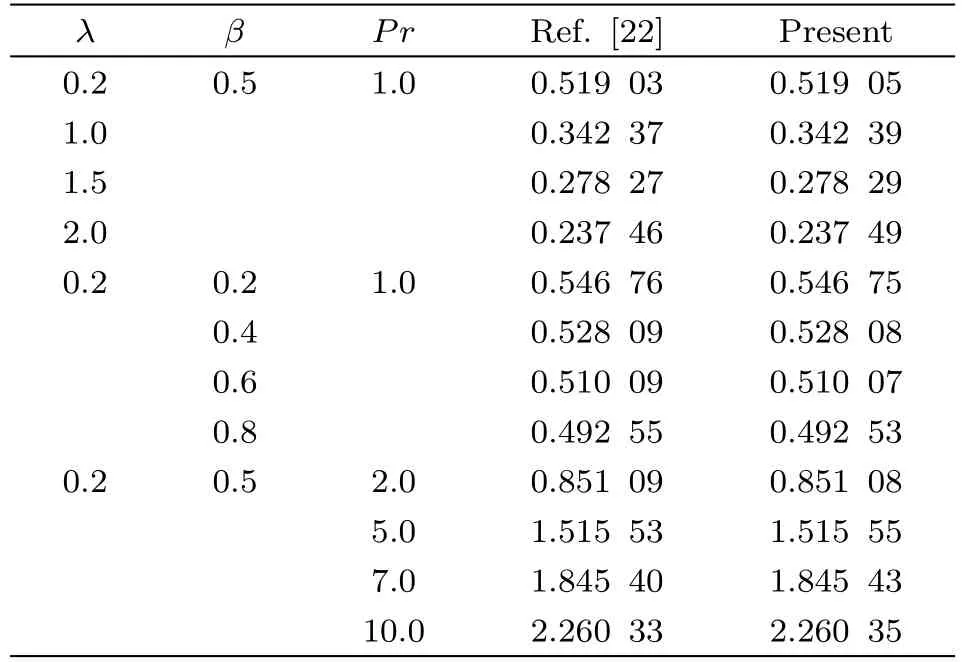
where ρ,p and Ω = [0,0,Ω]are fluid density,pressure and the angular velocity.The quantity Ω × (Ω ×r)= −∇(Ω2r2/2)denotes the centrifugal force which is well-adjusted by the pressure gradient−∇p.The term(T/T∞)ne−Ea/κTrepresents the modified Arrhenius function.[20]Here,k=8.61 × 10−5eV/K,and n(−1 and in Eq.(3),q is the heat flux satisfying the following relation where λ2and k represent the thermal relaxation time and fluid thermal conductivity.Considering the mass continuity equation∇·V=0 and the steady laminar flow with∂q/∂t=0.Also in Eq.(5),λ1,A1=(∇V)+(∇V)tand D/Dt are the fluid relaxation time, first Rivilin-Ericksen tensor and the upper-convected time derivative.Introducing boundary layer approximations,Eqs.(1)–(4)take the form where D,kf,and λ2are the diffusion coefficient,thermal conductivity of the fluid,and relaxation time of heat flux.For λ2=0,Eq.(5)is reduced to classical Fourier’s law and Fick’s law.Also,ν,T,cp,v and(u,v,w)are the kinematic viscosity,temperature,specific heat, fluid density and velocities along(x,y,z)directions respectively.Equations(7)–(11)are supported by the boundary conditions are Employing transformation Equation(7)is satisfied automatically and Eqs.(8)–(12)take the form where λ,β,Pr,Sc,E,δ,σm,δt,M,and γ1and γ2are the rotation parameter,Deborah number(ratio of relaxation time to time of observation),Prandtl number(quotient of momentum to thermal diffusivity),Schmidt number(quotient of momentum to mass diffusivity),non-dimensional activation energy,temperature difference parameter,dimensionless reaction rate,thermal relaxation time(ratio of time required by a tissue to cool midway towards its original temperature),magnetic parameter and thermal and concentration Biot numbers(quotient of resistance to the internal heat flow to resistance to external heat flow)respectively and are defined as: Local Nusselt and Sherwood numbers in dimensional form are where Dimensionless forms of Local Nusselt and Sherwood numbers are The system of ODEs is solved with MATLAB built-in function bvp-4c.It is a finite difference code that implements the three-stage Lobatto IIIa formula.This is a collocation formula and the collocation polynomial provides a C1-continuous solution that is fourth order accurate uniformly in[a,b].Mesh selection and error control are based on the residual of the continuous solution.It has the following Matlab syntax: sol=(bvp4c(@odefun;@bcfun;solinit;options).To apply this method,the system of nonlinear ODEs(14)–(17)is converted to the subsequent system of first order ODEs: We denote f by y1,g by y4,θ by y6and ϕ by y8for converting the boundary value problem to the following initial value problem(IVP) along with following boundary conditions All the computations are made with the tolerance of ε=10−6,using a verified Matlab code. In this section we have presented graphical illustrations depicting effects of varied prominent parameters on all involved profiles with requisite deliberations. Fig.2 Graph of f′versus β. λ =0.2,M=0.2,Pr=1.0,n=0.2,γ =0.1,δt=0.3,Sc=0.7,σm=0.5,δ=1.0,E=1.0. Fig.3 Graph of g versus β. λ =0.2,M =0.2,Pr=1.0,n=0.2,γ1= γ2=0.1,Sc=0.7,σm=0.5,δ=1.0,E=1.0,δt=0.3. Fig.4 Graph of f′versus λ. β =0.2,M=0.2,Pr=1.0,n=0.2,γ1= γ2=0.1,δt=0.3,Sc=0.7,σm=0.5,δ=1.0,E=1.0. Fig.5 Graph of g versus λ. β =0.2,M =0.2,Pr=1.0,n=0.2,γ1= γ2=0.1,δt=0.3,Sc=0.7,σm=0.5,δ=1.0,E=1.0. Fig.6 Graph of ϕ versus E. λ =0.2,β =0.2,Pr=1.0,n=0.2,γ1= γ2=0.1,δt=0.3,Sc=0.7,σm=0.5,δ=1.0. Fig.7 Graph of ϕ versus σm. λ =0.2,M=0.2,Pr=1.0,n=0.2,γ1= γ2=0.1,δt=0.3,Sc=0.7,β=0.2,δ=1.0,E=1.0. Figure 2 represents the behavior of Deborah number β on velocity field f′.From figure,it is witnessed that f′is decreasing function of β.This because of the fact that fluid’s motion in one direction is stymied by the viscoelastic effects.For smaller values of β,viscous effects are stronger than elastic and eventually fluid starts behaving like elastic solid material.However,for larger β,f′→ 0 near the sheet. Figure 3 is portrayed to visualize the influence of Deborah number β on g.From the graph,it is obvious that negative g values point out the fluid’s flow completely in y-direction.However,gradual increase in β shows that oscillations in g profile are more similar to that of f′. Fig.8 Graph of ϕ versus δ. λ =0.2,M =0.2,Pr=1.0,n=0.2,γ1= γ2=0.1,δt=0.3,Sc=0.7,σm=0.5,β =0.2,E=1.0. Fig.9 Graph of f′versus M. λ =0.2,β =0.2,Pr=1.0,n=0.2,γ1= γ2=0.1,δt=0.3,Sc=0.7,σm=0.5,δ=1.0,E=1.0. Fig.10 Graph of θ versus δt. λ =0.2,M=0.2,Pr=1.0,n=0.2,γ1= γ2=0.1,β =0.2,Sc=0.7,σm=0.5,δ=1.0,E=1.0. From Fig.4,it is noticed that velocity profile f′is decreasing function of rotation parameter λ.For λ =0,we have non-rotating frame.With gradual increment in λ,rotation rate will be stronger than the stretching rate and offer more resistance to the fluid’s motion.Eventually,a thinner boundary layer thickness with decrease in velocity distribution is observed. Figure 5 depicts the behavior of rotation parameter λ on velocity distribution g.It is noticed that an oscillatory pattern encountered for increasing values of λ which assist the flow in negative y-direction. Figure 6 is drawn to show the effects of dimensionless activation energy E on concentration distribution ϕ.Form figure,it is revealed that E is dwindling function of ϕ.Increasing values of E with low temperature results in smaller reaction rate constant and eventually slow chemical reaction is observed.This boosts the concentration’s solute. In Fig.7,impact of dimensionless constant rate σmon concentration field is portrayed. Higher values of σmweaken the concentration field that eventually supports the destructive chemical reaction. Fig.11 Graph of θ versus Pr. λ =0.2,M=0.2,β =0.2,n=0.2,γ1= γ2=0.1,δt=0.3,Sc=0.7,σm=1.0,δ=1.0,E=1.0. Fig.12 Graph of θ versus γ1. λ =0.2,M=0.2,Pr=1.0,n=0.2, γ2=0.1, δt=0.3,Sc=0.7,σm=0.5,δ=1.0,E=1.0. Figure 8 is illustrated to depict the influence of temperature difference parameter δ on concentration distribution.As the difference between the two temperatures(at the wall and far away from the wall)increases,a weaker concentration profile with thinner boundary layer thickness is witnessed. Fig.13 Graph of θ versus γ2. λ =0.2,M=0.2,Pr=1.0,n=0.2,β =0.2,δt=0.3,Sc=0.7,σm=0.5,δ=1.0,E=1.0. Table 1 Comparison of Local Nusselt number −θ′(0)for varied values of λ, β and Pr obtained by Shafique et al.[22]in the absence of magnetohydrodynamic and Cattaneo-Christov heat flux. From Fig.9,it is perceived that velocity distribution is dwindling function of magnetic parameter M.The reason of deteriorating velocity is stronger Lorentz force(because of gradually improving values of M)which ultimately oppose the fluid’s motion and forces it to slow down. Figure 10 is portrayed to show the influence of thermal relaxation time δton temperature distribution θ.From Fig.10,it is seen that θ is declining function of δt.Comparatively more time is required by material particles to pass on heat to adjacent particles with increasing thermal relaxation time.This feature of material resembles to partially insulated materials and has become a reason to lower the temperature. In Fig.11,effect of Prandtl number Pr on temperature field θ is displayed.For growing values of Pr,a weaker thermal diffusivity is noticed that ultimately drops the fluid’s temperature. Table 2 Sherwood number for varied values of Pr,δt,Sc,σm,δ,E and n when γ1= γ2= β =M=0.2. Figures 12 and 13 reveal that temperature and concentration distributions with their associated boundary layer thicknesses are augmented with mounting values of respective Biot numbers γ1and γ2.As temperature and concentration have direct proportionate with heat and mass transfer coefficients h1and h2respectively.That is why both distributions demonstrate increasing behavior for higher values of respective Biot numbers. Table 1 is erected numerically to give comparison with a previous study by Shafique et al.[22]in limiting case and all values are found in an excellent agreement.Table 2 represents the trend of Sherwood number against varied values of Pr,δt,Sc,σm,δ,n,E and by fixing other parameters λ,β,M,γ1and γ2.It is noticed that Sherwood number showns a declining behavior for Pr,δt,E and increasing tendency for Sc,σm,δ,n. In this exploration,we have studied numerical solution of 3D magnetohydrodynamic rotating flow of Maxwell fluid with binary chemical reaction,activation energy and Cattaneo-Christov heat flux using bvp-4c MATLAB.The key observations of the present study are: •Velocity is declining function of Deborah number and rotation parameter. •Activation energy and temperature difference parameters have opposite effects on concentration distributions. •With increase in thermal relaxation time and Prandtl number,decrease in temperature field is observed. •Temperature and concentration distributions demonstrate increasing behavior for respective Biot numbers. •Sherwood number shows a decreasing behavior for Prandtl number,thermal relaxation time,and nondimensional activation energy. Competing interests:The authors declare no competing interest. [1]S.Han,L.Zheng,C.Li,and X.Zhang,Appl.Math.Lett.38(2014)87. [2]M. Mustafa, AIP Adv. 5 (2015) 047109,http://dx.doi.org/10.1063/1.4917306. [3]M.Ramzan,M.Bilal,and J.D.Chung,Int.J.Chem.React.Eng.15(3)(2017)doi.org/10.1515/ijcre-2016-0136. [4]M.Ramzan,M.Bilal,and J.D.Chung,J.Mol.Liq.230(2017)4152. [5]M.Mustafa,T.Hayat,and A.Alsaedi,Int.J.Heat Mass Trans.106(2017)142. [6]M.I.Khan,T.Hayat,M.Waqas,et al.,J.Mol.Liq.233(2017)465. [7]I.Khan,N.A.Shah,and L.C.C.Dennis,Sci.Rep.7(2017),doi:10.1038/srep40147. [8]K.L.Hsiao,Appl.Therm.Engr.112(2017)1281. [9]T.Hayat,T.Muhammad,S.A.Shehzad,and A.Alsaedi,J.Mol.Liq.229(2017)495. [10]R.Jusoh,R.Nazar,and I.Pop,Int.J.Mech.Sci.124–125(2017)166. [11]J.Zhao,L.Zheng,X.Chen,et al.,Appl.Math.Modelling 44(2017)497. [12]A.Shahid,M.M.Bhatti,O.A.Bég,and A.Kadir,Neural Comput.Appl.(2017)1. [13]M.Ramzan,M.Bilal,J.D.Chung,and U.Farooq,Results Phys.6(2016)1072. [14]S.Bilal,K.U.Rehman,H.Jamil,and M.Y.Malik,AIP Adv.6(2016)125125. [15]F.Mabood,S.Shateyi,M.M.Rashidi,et al.,Adv.Powder Tech.27(2016)742. [16]S.Ahmed,J.Zueco,amd L.M.López-González,Int.J.Heat Mass Trans.104(2017)409. [17]A.R.Bestman,Int.J.Energy Res.14(1990)389. [18]O.D.Makinde,P.O.Olanrewaju,and W.M.Charles,Afrika Matematika 22(1)(2011)65. [19]K.A.Maleque,Thermodyn.2013(2013),Article ID 284637,9 pages. [20]F.G.Awad,S.Motsa,and M.Khumalo,PLoS ONE 9(2014)e107622. [21]M.Mustafa,J.A.Khan,T.Hayat,and A.Alsaedi,Int.J.Heat Mass Trans.108(2017)1340. [22]Z.Shafique,M.Mustafa,and A.Mushtaq,Results Phys.6(2016)627. [23]C.Y.Wang,Zeitschrift für angewandte Mathematik und Physik ZAMP 39(1988)177. [24]V.Rajeswari and G.Nath,Int.J.Engr.Sci.30(1992)747. [25]H.S.Takhar,A.J.Chamkha,and G.Nath,Int.J.Therm.Sci.42(2003)23. [26]M.Kumari,T.Grosan,and I.Pop,Technische Mechanik 1(2006)11. [27]K.Zaimi,A.Ishak,and I.Pop,Appl.Math.Mech.34(2013)945. [28]T.Javed,M.Sajid.Z.Abbas,and N.Ali,Int.J.Num.Meth.Heat&Fluid Flow 21(2011)903. [29]M.Mustafa,AIP Adv.5(2015)047109. [30]M.Turkyilmazoglu,Comput.&Fluids 90(2014)51. [31]T.Hayat,T.Muhammad,S.A.Shehzad,and A.Alsaedi,Comput.Meth.Appl.Mech.Eng.315(2017)467. [32]M.Mustafa,T.Hayat,and A.Alsaedi,Int.J.Heat Mass Trans.106(2017)142. [33]M.Ramzan,J.D.Chung,and N.Ullah,Results Phys.7(2017)3557. [34]M.Ramzan,M.Bilal,and J.D.Chung,J.Mol.Liq.225(2017)856. [35]M.E.Hakiem,M.Ramzan,and J.D.Chung,J.Comput.Theor.Nanosci.13(2017)8419. [36]J.B.J.Fourier,Theorie Analytique Da La Chaleur,Paris(1822).









3 Numerical Solutions



4 Results and Discussions


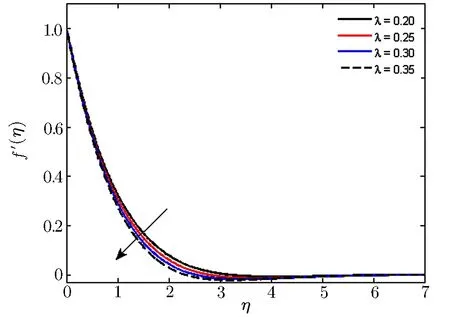
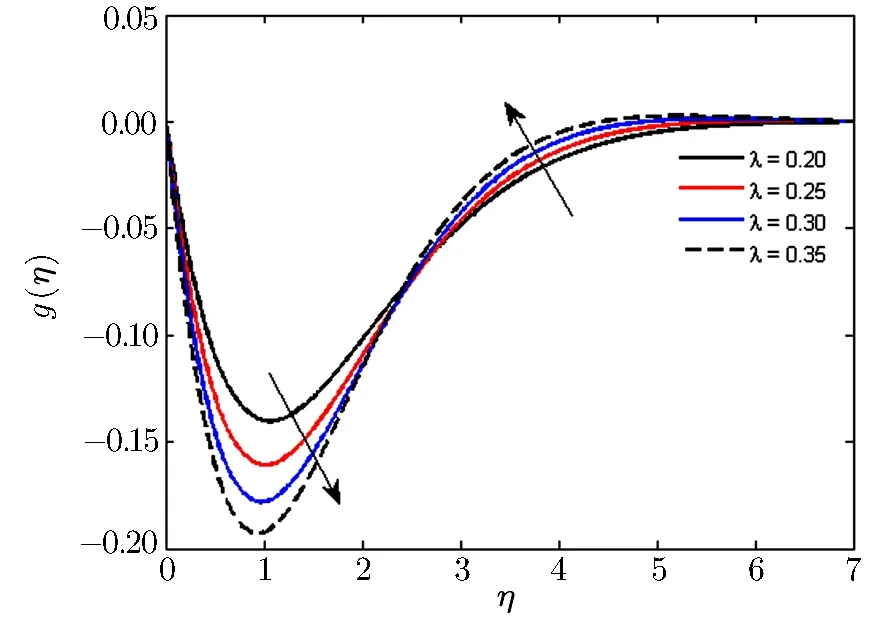


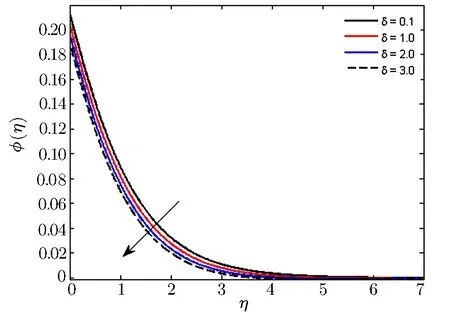




5 Final Remarks
杂志排行
Communications in Theoretical Physics的其它文章
- Transverse Transport of Polymeric Nano fluid under Pure Internal Heating:Keller Box Algorithm
- Detection of Magnetic Field Gradient and Single Spin Using Optically Levitated Nano-Particle in Vacuum∗
- Electron Correlations,Spin-Orbit Coupling,and Antiferromagnetic Anisotropy in Layered Perovskite Iridates Sr2IrO4∗
- Upshot of Chemical Species and Nonlinear Thermal Radiation on Oldroyd-B Nano fluid Flow Past a Bi-directional Stretched Surface with Heat Generation/Absorption in a Porous Media∗
- A New Calculation of Rotational Bands in Alpha-Cluster Nuclei
- The Three-Pion Decays of the a1(1260)∗
