Upshot of Chemical Species and Nonlinear Thermal Radiation on Oldroyd-B Nano fluid Flow Past a Bi-directional Stretched Surface with Heat Generation/Absorption in a Porous Media∗

Dian-Chen Lu,M.Ramzan,M.Bilal,Jae Dong Chung,and Umer Farooq5Department of Mathematics,Faculty of Science,Jiangsu University,Zhenjiang 220,China

2Department of Computer Science,Bahria University,Islamabad Campus,Islamabad 44000,Pakistan

3Department of Mathematics,Faculty of Computing,Capital University of Science and Technology,Islamabad 44000,Pakistan

4Department of Mechanical Engineering,Sejong University,Seoul 143-747,Korea

5Department of Mathematics,COMSATS Institute of Information Technology,Park road,Tarlai Kalan,Islamabad 45550,Pakistan

Nomenclature

1 Introduction

Heat and mass transfer is the most studied subject in today’s research because of its abundant efficacy in science and industry.The processes of reheating and freezing have vast usage in industry.In manufacturing processes,it is necessary to keep heat transfer phenomenon live in manufacturing of final refined product.Due to such interesting applications,scientists and researchers are captivated to reassess the potential of heat transfer.Choi and Eastman[1]were the pioneer who introduced the concept of great nanofluids to meet requirements of the industry.Geothermal industry, floor heating,polymer industry and processes like lubrication,manufacturing,chemical are some applications of nanofluids.A nanofluid is an amalgamation of nano sized metallic particles(like Cu,TiO2,Ag,etc.)and base fluid(like water,kerosene,ethylene glycol,oils).Usually,thermal conductivity of nanoparticle is more than the base liquid.However,mixture of both has obviously enhanced thermal conductivity.The pioneering work of Choi and Eastman was followed a study by Wang and Mujumdar[2]who tried to improve the convective characteristics of base fluid by insertion of metallic and nonmetallic nanoparticles.Then Eastman et al.[3]examined that mixture of ethylene glycol and suspended copper nanoparticles augments the thermal conductivity of the base fluid by 40%.In continuation to previous study,[3]Eastman et al.[4]explored another important result that thermal conductivity of nanofluid is also affected by the nanoparticle’s shape and size.This concept was supported by an experiment by Murshed et al.[5]who investigated that an amalgamation of spherical shaped nanoparticles(with size more than 40 nm)and Titanium oxide(base fluid)produces 33%more thermal conductivity than that of ordinary base fluid.In very a recent exploration,Pryazhnikov et al.[6]studied that thermal conductivity of nanofluid is also affected by nanoparticle’s material and density.Sandeep and Reddy[7]discussed the heat transfer phenomenon of Cu-water nanofluid past two varied geometries accompanied by nonlinear radiation effects.Zaib et al.[8]discussed the flow of Carreau nanofluid with effects of nonlinear thermal radiation,activation energy and binary chemical reaction past a nonlinear stretched surface.Nayak et al.[9]reported numerical treatment of three-dimensional nanofluid free convective flow with thermal radiation and magnetohydro dynamic with shooting technique.Kasaeian et al.[10]described heat transfer of nanofluids flow in a porous medium.Some more studies highlighting different aspects of nanofluids may be found at Refs.[11–20]and many therein.

Characteristics of viscoelasticity is key to many complex natured fluids like polymer melts,colloidal suspensions and polymer solutions.Applications like blow molding,inkjet printing and extrusion involve such fluids.Viscoelastic characteristics like energy dissipation,hydraulic resistance,transport efficiency etc.affect many flows.[21]Pioneering work of Maxwell[22]featured a rate type mathematical model to assess viscoelasticity in fluids.While doing so,he overlooked the incompressibility feature of the fluid.This gap is fulfilled by Oldroyd’s model[23]that portraits a factual depiction of nonlinear fluids.Amongst the proposed mathematical models by Oldroyd,Oldroyd-B model was much praised and admired model that interpret the both relaxation and retardation times’characteristics.This fluid model reduces to Maxwell fluid model in absence of retardation time term.Later,Lai[24]analyzed the stability of Oldroyd-B fluid down an inclined plane.This effort was followed by Thien[25]who discussed numerical and analytical solutions of Oldroyd-B fluid flow around a coaxial disk.Thien also highlighted stagnation point Oldroyd-B fluid flow[26]and instability of cone and plate.[27]Then Tan[28]extended Stokes’s first problem to Oldroyd-B fluid flow with semi permeable surface using sine transform to find exact solution.Exploring a new dimension,Fetecau et al.[29]found exact solutions of oscillating flows of Oldroyd-B fluid in oscillating circular cylinders.Pioneering work in three dimensional geometry was explored by Hayat et al.[30]who examined similar solution of three dimensional Oldroyd-B fluid flow past a bidirectional stretched surface.Boundary layer flow of an Oldroyd-B fluid over the continuously linearly stretching sheet is studied by Hayat et al.[31]They have examined the effects of mixed convection and stagnation point flow of thermally stratified fluid by using the homotopy analysis method.Waqar et al.[32]addressed analytically about the bidirectional flow of an Oldroyd-B nanofluid with heat generation/absorption over the stretching sheet.They concluded that local Nusselt number decreases for the higher values of heat generation parameter.Later on Hayat et al.[33]investigated about the electrically conducting Oldroyd-B nanofluid flow over the multidimensional stretching sheet with the zero nanoparticle mass flux condition employed on the boundary.They also applied normal magnetic field and found that velocity reduces for the higher magnetic strength.Zhang et al.[34]analyzed analytically the unsteady thin film flow of an Oldroyd-B nanofluid for the heat transfer over the stretching sheet.Poly vinyl alcohol-water is used as a base fluid with Ag and Cu as nanoparticles.Besides this,a good number of recent explorations highlighting various aspects involving three dimensional flows of Oldroyd-B fluid may be found in the literature.[35−38]However,after the invent of nanofluids,researchers started to explore new fronts with the amalgamation of Oldroyd-B fluid and nanofluids.First step in this direction was taken by Nadeem et al.[39]who studied flow of Oldroyd-B nanofluid flow past a linearly stretched surface numerically.Moving a step further,three dimensional nanofluid Oldroyd-B fluid past a stretched surface was deliberated by Khan et al.[39]Then Hayat et al.[40]studied three dimensional Oldroyd-B nanofluid with effects of magneto hydrodynamic and zero mass flux condition.Shehzad et al.[41]first time studied combination of linear thermal radiation with three dimensional Oldroyd-B nanofluid flow and magneto hydrodynamic.Last attempt in this regard is recently done by Hayat et al.[42]who found analytical solution of three dimensional Oldroyd-B nanofluid flow with heat generation/absorption.

From the above literature survey,it is revealed that the problem of three-dimensional Oldroyd-B magneto nanofluid flow with impact of nonlinear thermal radiation and chemical reaction in a porous media is still a scarce.Additional effects of heat generation/absorption,temperature dependent thermal conductivity and convective heat and mass conditions are added features to the uniqueness of the present effort.No attempt so far has been made to solve such an important mathematical model.We being the pioneer have solved this problem using renowned Homotopy Analysis method.[43−48]Graphical illustrations are given to portray the impact of varied parameters versus velocity profile,heat and mass transfer rates.To authenticate our results,a comparison with previous study in limiting case is also given.

2 Mathematical Formulation

Consider the flow of three-dimensional Oldroyd-B nanofluid past a bidirectional stretched surface in the presence of nonlinear thermal radiation in a porous media.Flow analysis is performed in attendance of thermophoresis and Brownian motion.Additional effects of heat generation,chemical reaction and variable thermal conductivity are also taken into account.Fluid flow occupies the region z>0,however,stretched surface coincides with the plane z=0.Fluid is made electrically conducting in the presence of uniform magnetic field of strength B0.Here,induced magnetic field is ignored due to our assumption of small Reynolds number.The velocity components u=cx and υ=dy(with c and d are constants)are along x and y-directions.Also,Twis the constant surface temperature and T∞is the ambient temperature with Tw>T∞(see Fig.1).The pertinent boundary layer equations are[33,49]

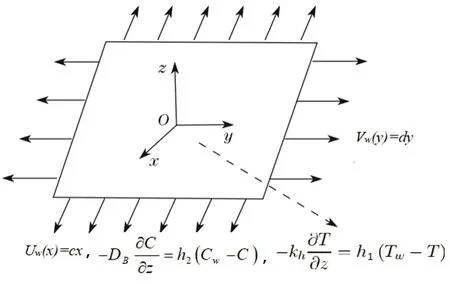
Fig.1 Geometry of the flow problem.

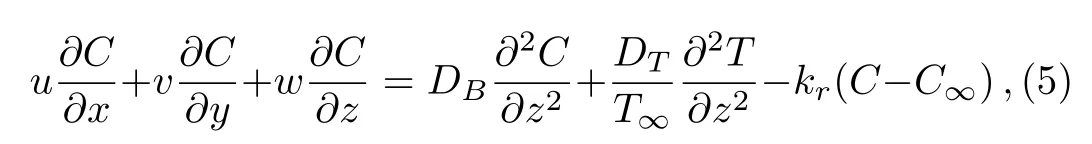
with(u,v,w)are the velocities along(x,y,z)directions respectively.

In view of Rosseland’s approximation,the value of heat flux is given by

The model equations(1)–(5)are supported by the boundary conditions Taking into account the succeeding transformations

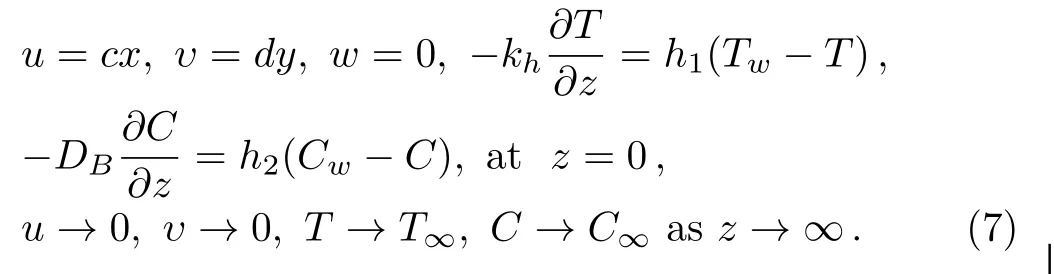
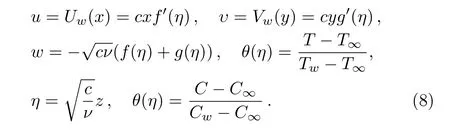
Here,η is similarity variable.The variable thermal conductivity[50]is given by k=k∞(1+θ(η)),where=(kw−k∞)/k∞with k∞and kware the fluid free stream conductivity and the thermal conductivity at wall respectively.Also,using the relation T=T∞((θw− 1)θ(η)+1),θw=Tw/T∞with above transformations,requirement of Eq.(1)is fulfilled inevitably,however,Eqs.(2)–(5)and Eq.(7)take the form

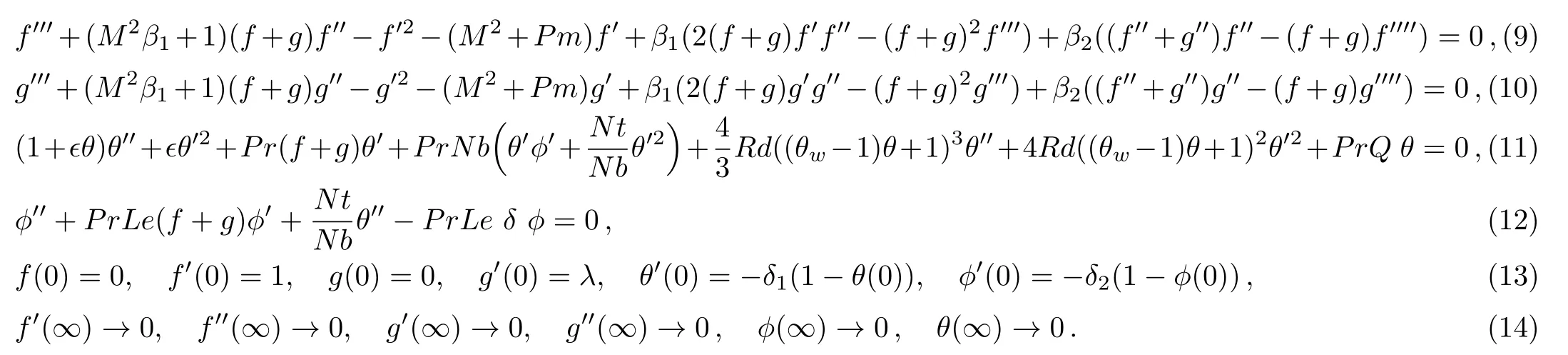
The values of above mentioned non-dimensionalized parameters are given below:

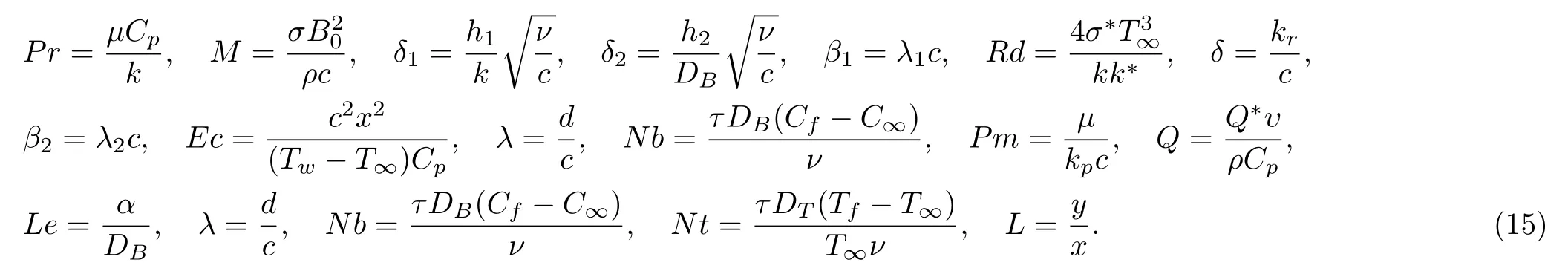
The heat and mass transfer rates i.e.,local Nusselt and Sherwood numbers in dimensional form are given by

where

Dimensionless form of these numbers are

3 Homotopic Solutions

The initial guesses(f0,g0,θ0,ϕ0)and linear operators(Lf,Lg,Lθ,Lϕ)required for Homotopy Analysis method are defined as:

with the following properties

where Ci(i=1–10),the arbitrary constants,through the boundary conditions have the values

3.1 Convergence Analysis

To determine the region of convergence for series solutions,the importance of auxiliary parameters(}f,}g,}θ,}ϕ)can not be denied.Figure 2 is illustrated to identify the same regions.Tolerable ranges of parameters}f,}g,}θ,and}ϕare−1.7≤ }f≤ −0.7,−1.6≤ }g≤−0.4,−1.4≤ }θ≤ −0.5,and−1.4≤ }ϕ≤ −0.5 respectively.The values of these parameters are in complete alignment to those numerical values found in Table 1.

Fig.2 }-curve of f,g,θ,and ϕ.

Table 1 Convergence of series solutions for different order of approximations when β1=0.2,β2=0.2,M=0.4,=0.3,λ =0.3,Nt=0.2,Nb=0.7,Rd=0.4,θw=1.3,Le=0.7,Pr=0.7,δ1=0.4,δ2=0.6,δ=0.2,Pm=0.1,Q=0.1.

Table 1 Convergence of series solutions for different order of approximations when β1=0.2,β2=0.2,M=0.4,=0.3,λ =0.3,Nt=0.2,Nb=0.7,Rd=0.4,θw=1.3,Le=0.7,Pr=0.7,δ1=0.4,δ2=0.6,δ=0.2,Pm=0.1,Q=0.1.

Order of approximations −f′′(0) −g′′(0) −θ′(0) −ϕ′(0)1.099 07 0.271 76 0.149 92 0.157 14 5 1.134 71 0.276 55 0.133 18 0.149 90 10 1.139 61 0.278 62 0.125 29 0.147 39 15 1.140 98 0.279 35 0.120 97 0.146 28 20 1.141 59 0.279 69 0.118 08 0.145 64 25 1.141 91 0.279 88 0.115 96 0.145 22 30 1.142 12 0.279 99 0.114 30 0.144 93 35 1.142 14 0.280 03 0.114 00 0.144 83 40 1.142 14 0.280 03 0.113 93 0.144 82 1

4 Results and Discussion

This section is outlined to examine the impact of varied involved parameters on all distributions via several graphs that arise in the mathematical model.Figures 3 and 4 are drawn to show the influence of relaxation and retardation times i.e.,β1and β2on velocity fields f′(η)and g′(η)respectively.It is witnessed that f′(η)and g′(η)are decreasing and increasing functions of β1and β2respectively.This is due to the fact that higher values of β1boosts the viscous force that hinders the movement of fluid’s motion and eventually decays in velocity profile is seen.An opposite trend in case of β2is seen where growth in velocity field is observed for large values of β2.Here,strength of viscous force is weakened because of higher values of β2and eventually an enhanced velocity distribution is perceived.Figures 5 and 6 epitomize the impact of Biot numbers δ1and δ2on temperature and concentration fields respectively.Both δ1and δ2have direct proportion to their respective heat and mass transfer coefficients.Augmented values of δ1and δ2are because of more heat and mass transfer resistance inside the body in comparison to the surface that results in enhanced temperature and concentration distributions.Figure 7 elucidates the impact of temperature dependent thermal conductivity parameteron temperature distribution.It is noticed that increasing values ofamplify the temperature field.As we know that higher temperature is because of increased values of thermal conductivity.In Fig.8,effect of heat generation/absorption parameter Q on temperature distribution is displayed.It is perceived that mounting values of Q lead to increase in the temperature profile.Higher values of Q means more heat is transferred to the fluid that ultimately results in higher temperature and sturdier boundary layer thickness.Figures 9 and 10 are portrayed to depict the effect of stretching ratio parameter λ on both velocities f′(η)and g′(η)respectively.It is seen that higher value of λ is in direct and indirect relation to stretched rates along y-and x-directions respectively.So,velocity field g′(η)along y-direction increases and velocity field f′(η)along x-direction decreases.

Fig.3 Graph of β1versus f′(η).

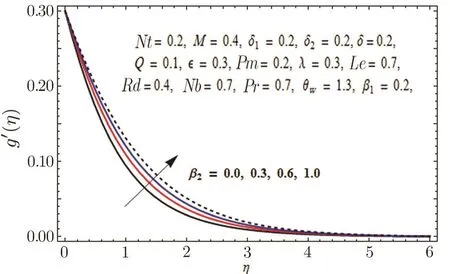
Fig.4 Graph of β2versus g′(η).

Fig.5 Graph of δ1versus θ(η).

Fig.6 Graph of δ2versus ϕ(η).

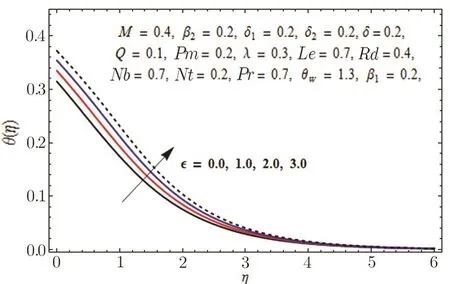
Fig.7 Graph of versus θ(η).

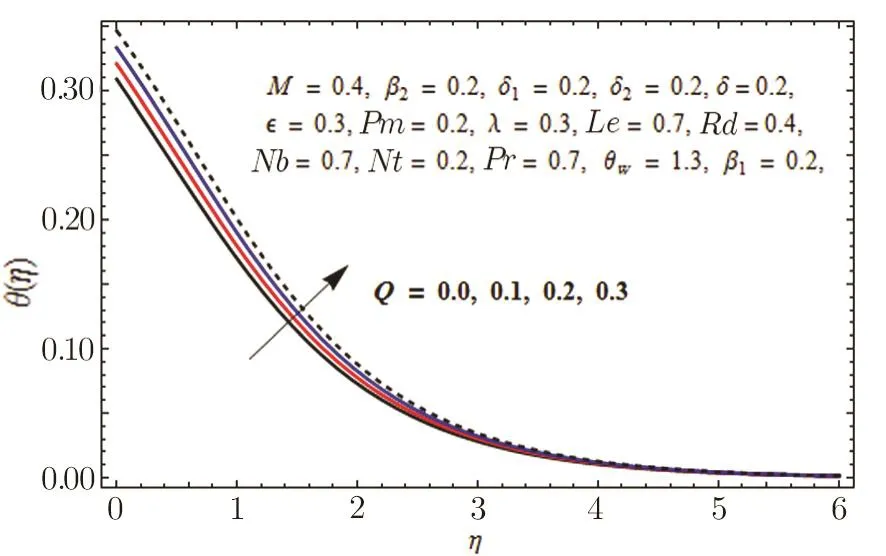
Fig.8 Graph of Q versus θ(η).

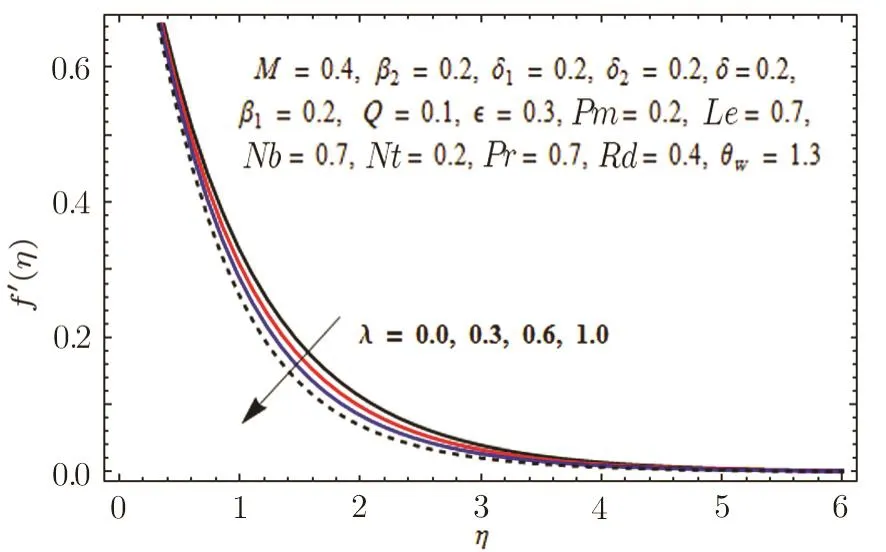
Fig.9 Graph of λ versus f′(η).

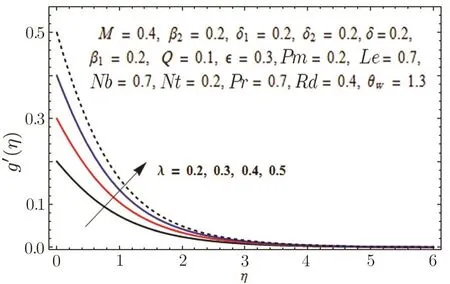
Fig.10 Graph of λ versus g′(η).

In Fig.11,impact of radiation parameter Rd on temperature distribution is presented.It is examined that temperature field is mounted function of Rd.It is due to the fact that enhancement in thermal radiation parameter results in diminution in mean absorption coefficient that eventually boosts the divergence of the radiative heat flux and increase in fluid’s temperature is witnessed.Figure 12 is drawn to show the impact of Lewis number Le on concentration distribution.As we know that Lewis number is the quotient of thermal diffusivity to mass diffusivity.Increase in Le means high thermal diffusivity which is responsible for decrement in concentration distribution.Figures 13 and 14 are illustrated to depict the influence of Hartmann number M on velocities in both x-and y-directions respectively.It is seen that both velocities decrease with increase in values of M.This is because of the resistance offered by the Lorentz force.Hence,decrease in both velocities is experimented.Figure 15 is portrayed to depict the effect of temperature ratio parameter θwon temperature field.Augmented values of θwenhance the fluid’s thermal state,which is accountable for increased temperature.In Fig.16,effect of Brownian motion parameter Nb on temperature profile is portrayed.It is examined that temperature field is increasing function of Nb.Actually,rise in values of means Nb more collision of particles and eventually rise in temperature field is witnessed.Figure 17 is drawn to illustrate the impact of thermophoresis parameter Nt on concentration profile.Decrease in concentration profile is seen for increasing values of Nt.Nanoparticles are attracted towards the cold surface with increase in values of Nt that lowers the nanoparticle concentration.To check the influence of Prandtl number Pr on temperature and concentration distributions,Figs.18 and 19 are graphed.

Fig.11 Graph of Rd versus θ(η).

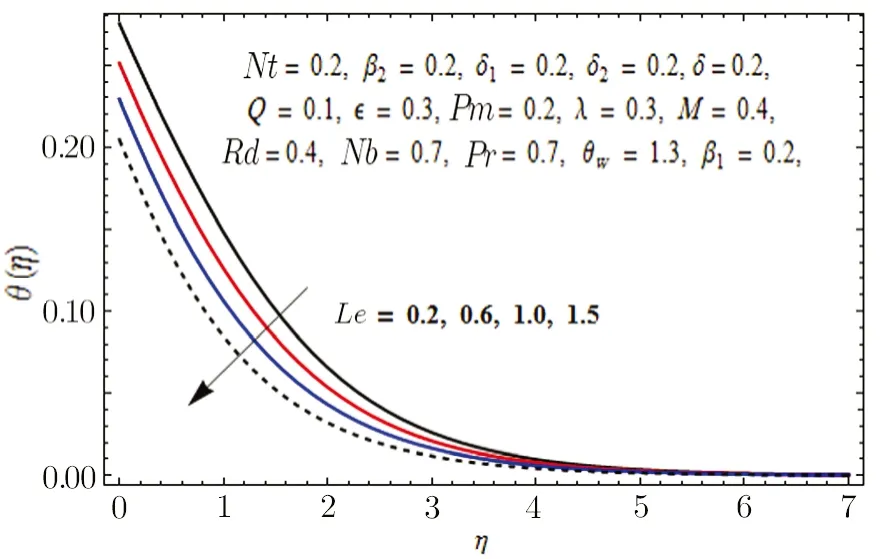
Fig.12 Graph of Le versus ϕ(η).

Fig.13 Graph of M versus f′(η).

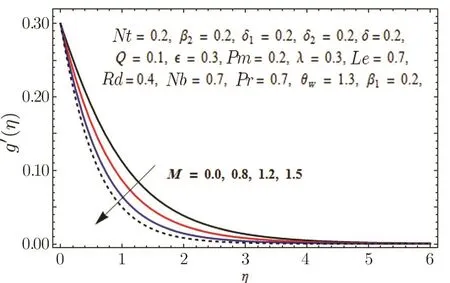
Fig.14 Graph of M versus g′(η).

Fig.15 Graph of θwversus θ(η).

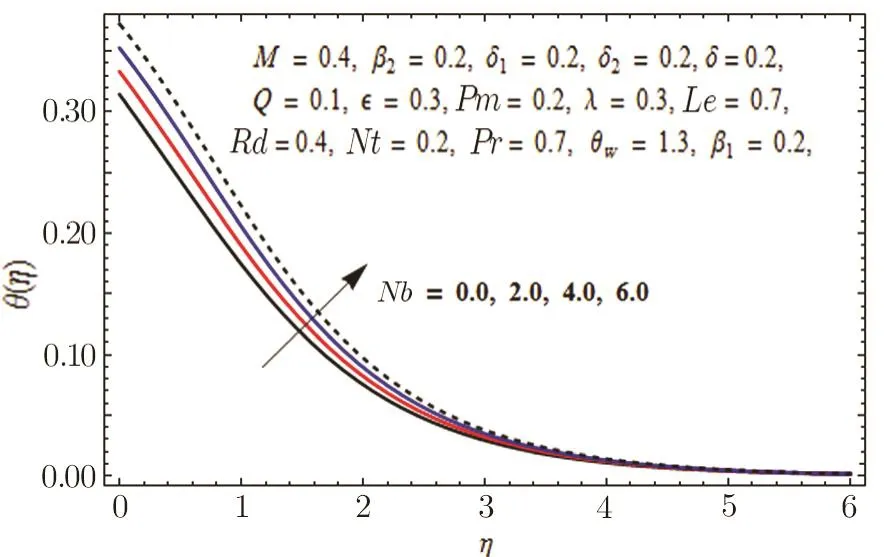
Fig.16 Graph of Nb versus θ(η).

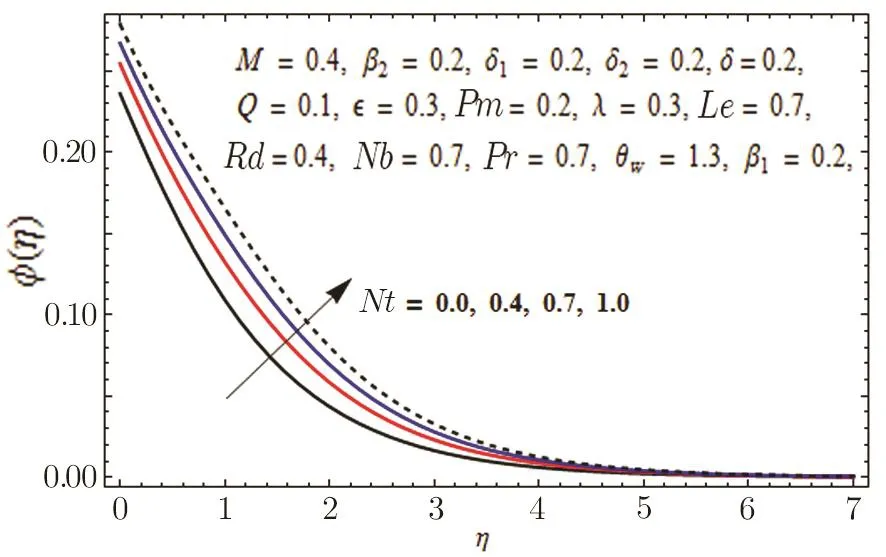
Fig.17 Graph of Nt versus ϕ(η).

Fig.18 Graph of Pr versus θ(η).

Fig.19 Graph of Pr versus ϕ(η).

Fig.20 Graph of Pm versus g′(η).

Fig.21 Graph of δ<0 versus ϕ(η).

Fig.22 Graph of δ>0 versus ϕ(η).

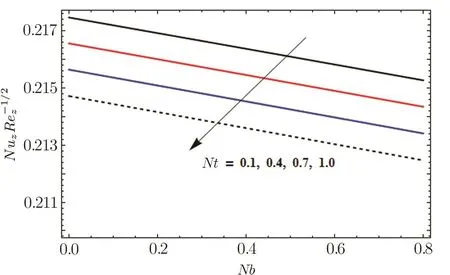
Fig.23 Influence of Nb and Nt on Nuz

Fig.24 Influence of Pr and Rd on Nuz

It is experimented that Prandtl number is the proportion of momentum diffusivity to thermal diffusivity.Higher values of momentum diffusivity correspond to feeble thermal diffusivity in case of Prandtl number and we encounter weaker boundary layer thicknesses in case of both temperature and concentration profiles.Figure 20 is drawn to exhibit the effects of permeability parameter Pm on velocity profile along y-axis.It is seen that porous medium offers resistance to the fluid flow and as a result velocity of the fluid is decreased.Effect of chemical reaction parameter in both cases generative(δ<0)and destructive(δ>0)on concentration profile is presented in Figs.21 and 22 respectively.Opposite behavior in both cases is witnessed.Disruption in chemical reaction for generative case(δ<0)does not create much disorder.However,in case of destructive(δ>0),disruption is higher due to comparatively substantial molecular motion.

Table 2 Values of local Nusselt number −θ′(0)in comparison to Hayat et al.[50]for different values of parameters β1, β2,Pr and γ in absence of nanofluid,nonlinear thermal radiation,variable thermal conductivity,porous medium,chemical reaction,convective mass condition.

Fig.25 Influence of Pr and Le on Shz

Figures 23 and 24 show that Nusselt number increase and decrease for gradual increasing values of Pr,Rd and Nt,Nb respectively.In Fig.25,we see that Sherwood number increase and decrease for Le and Pr respectively.

Table 2 depicts an excellent agreement of numerically calculated local Nusselt number in limiting case(in absence of nanofluid,nonlinear thermal radiation,variable thermal conductivity,porous medium,chemical reaction,convective mass condition)to those values obtained Hayat et al.[50]

5 Conclusions

In this communication three-dimensional Oldroyd-B fluid flow in attendance of variable thermal conductivity and nonlinear thermal radiation is studied.Additional effects of chemical reaction,porous medium and magneto hydrodynamics are also taken into account.Flow analysis is performed in the presence Brownian motion and thermophoresis with convective heat and mass conditions.The salient characteristics of this investigation are appended below:

•Increasing values of radiation parameter boosts the temperature of fluid.

•Convective heat and mass transfer support the temperature and concentration profiles respectively.

•Higher values of variable thermal conductivity augments the fluid’s temperature.

•Sherwood number increases with higher values of Prandtl and Lewis numbers.

•Velocities along x-and y-axes decrease with increase in values of Hartmann number.

•Temperature is increased with higher values of Brownian motion.

•Opposite behavior in case of generative and destructive chemical reaction on concentration field is witnessed.

•Decrease in velocity of fluid flow is observed for increasing values of permeability parameter.

[1]S.U.S.Choi and J.A.Eastman,ASME Inter.Mech.Eng.Cong.Expo.66(1995)99.

[2]X.Q.Wang and A.S.Mujumdar,Int.J.Thermal Sci.46(2007)46.

[3]J.A.Eastman,S.R.Phillpot,S.U.S.Choi,and P.Keblinski,Annual Review Mater.Res.34(2004)219.

[4]J.A.Eastman,S.U.S.Choi,S.Li,W.Yu,and L.J.Thompson,Appl.Phys.Lett.78(2001)718.

[5]S.M.S.Murshed,K.C.Leong,and C.Yang,Int.J.Thermal Sci.44(2005)367.

[6]M.I.Pryazhnikov,A.V.Minakov,V.Y.Rudyak,and D.V.Guzei,Int.J.Heat Mass Tran.104(2017)1275.

[7]N.Sandeep and M.G.Reddy,J.Mol.Liq.225(2017)87.

[8]A.Zaib,M.M.Rashidi,A.J.Chamkha,and N.F.Mohammad,Proceedings of the Institution of Mechanical Engineers,Part C:J.Mech.Engr.Sci.(2017)doi.org/10.1177/0954406217695847.

[9]M.K.Nayak,N.S.Akbar,V.S.Pandey,et al.,Powder Technol.315(2017)205.

[10]A.Kasaeian,R.D.Azarian,O.Mahian,et al.,Int.J.Heat Mass Tran.107(2017)778.

[11]M.Ramzan,J.D.Chung,and N.Ullah,Int.J.Mech.Sci.130(2017)31.

[12]M.Ramzan,M.Bilal,and J.D.Chung,Chin.J.Phys.55(2017)1663.

[13]M.Ramzan,M.Bilal,and J.D.Chung,PLoS ONE 12(2017)e0170790.

[14]M.Ramzan,M.Bilal,J.D.Chung,and A.B.Mann,Neural Comput.Appl.(2017)doi.org/10.1007/s00521-017-2852-8.

[15]M.Meraj,S.A.Shehzad,T.Hayat,et al.,Appl.Math.Mech.38(2017)557.

[16]M.Ramzan,F.Yousaf,M.Farooq,and J.D.Chung,Commun.Theor.Phys.66(2016)133.

[17]M.Ramzan,S.Inam,and S.A.Shehzad,Alexandria Engr.J.55(2016)311.

[18]M.Ramzan and M.Bilal,J.Mol.Liq.215(2017)212.

[19]M.A.El-Hakiem,M.Ramzan,and J.D.Chung,J.Comput.Theor.Nanosci.13(2016)8419.

[20]S.Shaw,P.K.Kameswaran,and P.Sibanda,Bound.Value Prob.2016(2016)2.

[21]R.Comminal,J.H.Hattel,M.A.Alves,and J.Spangenberg,J.Non-Newtonian Fluid Mech.237(2016)1.

[22]J.C.Maxwell,Philosophical Transactions of the Royal Society B:Biological Sciences 157(1867)49.

[23]J.G.Oldroyd,P.Roy.Soc.Lond.A:Math.Phys.Sci.200(1950)523.

[24]W.Lai,Phys.Fluids 10(1967)844.

[25]N.P.Thien,J.Non-Newtonian Fluid Mech.13(1983)325-340.

[26]N.P.Thien,Rheologica Acta 23(1984)172.

[27]N.P.Thien,J.Non-Newtonian Fluid Mech.17(1985)37.

[28]W.Tan,Phys.Fluids 17(2005)023101.

[29]T.Hayat,A.M.Siddiqui,and S.Asghar,Int.J.Eng.Sci.39(2001)135.

[30]T.Hayat,S.Nadeem,and S.Asghar,Int.J.Eng.Sci.42(2004)65.

[31]T.Hayat,Z.Hussain,M.Farooq,et al.,Int.J.Nonlinear Sci.Numer.Simul.15(2014)77.

[32]W.A.Khan,M.Khan,and R.Malik,PLoS ONE 9(2014)e105107.

[33]T.Hayat,T.Muhammad,S.A.Shehzad,et al.,J.Mol.Liquids 212(2015)272.

[34]Y Zhang,M.Zhang,and Y.Bai,J.Mol.Liquids 220(2016)665.

[35]S.Hina,M.Munira,and M.Mustafa,Int.J.Mech.Sci.131(2017)146.

[36]T.Hayat,S.Farooq,A.Alsaedi,and B.Ahmad,Int.J.Thermal Sci.112(2017)68.

[37]M.S.Hashmi,N.Khan,T.Mahmood,and S.A.Shehzad,Int.J.Thermal Sci.111(2017)463.

[38]N.Sandeep and M.G.Reddy,Eur.Phys.J.Plus 132(2017)147.

[39]W.A.Khan,M.Khan,and R.Malik,PLoS ONE 9(2014)e105107.

[40]T.Hayat,T.Muhammad,S.A.Shehzad,et al.,J.Mol.Liq.212(2015)272.

[41]S.A.Shehzad,Z.Abdullah,F.M.Abbasi,et al.,J.Magn.Magn.Mater.399(2016)97.

[42]T.Hayat,T.Muhammad,S.A.Shehzad,and A.Alsaedi,Int.J.Thermal Sci.111(2017)274.

[43]M.Ramzan,M.Bilal,and J.D.Chung,Int.J.Chem.Reactor Eng.15(2017)doi.org/10.1515/ijcre-2016-0136.

[44]M.Ramzan,M.Bilal,and J.D.Chung,J.Mol.Liq.230(2017)415.

[45]M.Ramzan,M.Bilal,and J.D.Chung,J.Mol.Liq.223(2016)1284.

[46]T.Hayat,M.Waqas,S.A.Shehzad,and A.Alsaedi,Euro.Phys.J.Plus 131(2016)253.

[47]T.Hayat,M.Zubair,M.Ayub,et al.,Euro.Phys.J.Plus 131(2016)355.

[48]T.Hayat,M.I.Khan,M.Waqas,and A.Alsaedi,Nucl.Eng.Tech.49(2017)1645.

[49]T.Hayat,S.A.Shehzad,A.Alsaedi,and M.S.Alhothuali,Appl.Math.Mech.34(2013)489.

[50]H.Zargartalebi,M.Ghalambaz,A.Noghrehabadi,and A.Chamkha,Adv.Powder Technol.26(2015)819.