A Quantum Multi-Proxy Blind Signature Scheme Based on Entangled Four-Qubit Cluster State∗

Xu-Feng Niu(牛旭峰),Jian-Zhong Zhang(张建中),,† and Shu-Cui Xie(谢淑翠)2College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 709,China

2School of Science,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

1 Introduction

Digital signature is one of the most important parts in cryptography. It is an important technique to authenticate the identity and ensure the integrity of legal messages.It has been widely used in E-voting protocols,E-commerce systems and so on.However,the security of classical signature schemes depends on some computational problems that may be solved using quantum algorithms.[1−2]The security of quantum cryptography relies on the principles of quantum mechanics,thus quantum signature has attracted much attention.In 2001,Gottesman and Chuang proposed the first quantum signature scheme in Ref.[3].Then Buhrman et al.[4]and Barnum et al.[5]made some significant attempts about quantum signature respectively.More recently,some other kinds of quantum signature schemes were presented,such as quantum multiple signature and quantum group signature.[6−7]

As an important cryptographic primitive,proxy signature was first introduced by Mambo,Usada,and Okamoto in 1996.[8]It allows a proxy signatory on behalf of an original signatory to sign a message.A quantum proxy signature scheme with public verifiability was presented by Zhou et al.[9]More recently,some quantum proxy signature schemes were presented.For example,Xu proposed a novel quantum proxy signature without entanglement.[10]In 2017,Yang et al.implemented a quantum proxy blind signature schemes with Genuine Seven-Qubit Entangled State.[11]In addition,Zeng et al.proposed a quantum proxy blind signature scheme.[12]

In 1982,a blind signature was introduced by David Chaum.[13]It is called blind signature if the signatory generates a signature without revealing any information of the message.[13]Subsequently,blind quantum signature has attracted much attention.For example,in 2010,Wang et al.proposed a fair quantum blind signature scheme.[14]In 2016,Shao et al.proposed a quantum multi-proxy multiblind-signature scheme combing the requirement for the proxy and blind signature scheme.[15]In addition,Guo et al.proposed a feasible blind quantum signature scheme.[16]

Our multi-proxy blind signature scheme has a wide application in practical life.For example,a company’s president needs to sign an important and private document when he is temporal absence,he will delegate a group of department managers not a single one to blindly sign the document in order to prevent abuse of the signing authority and avoid exposure of the sensitive information.

The paper is outlined as follows:In the next section,we introduce the controlled quantum teleportation.In Sec.3,we describe the quantum multi-proxy blind signature scheme in detail.The security analysis and discussion are presented in Sec.4.Finally,conclusions are drawn in Sec.5.

2 Controlled Quantum Teleportation

Our multi-proxy blind signature scheme is based on the controlled quantum teleportation,which takes the entangled four-qubit Cluster state as its quantum channel.It is given by

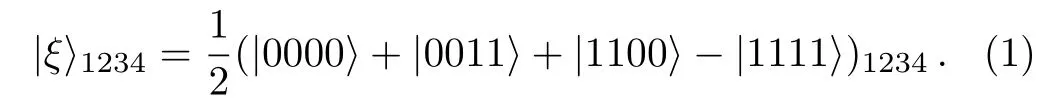
As shown in Fig.1,this controlled quantum teleportation involves the following three partners:a sender Alice,a controller Charlie,and a receiver Bob.Alice holds particles(1,3),Charlie,and Bob own particle 4 and particle 2,respectively.

Fig.1 The model of quantum teleportation.

Suppose that the quantum state of particle carrying message in Alice is

where the coefficients α and β are unknown and satisfy|α|2+|β|2=1.

The system quantum state composed of particle M and(1,2,3,4)is given by

(i)Alice performs a von Neumann measurement on particle M and particles(1,3)with the basiswhere the quantum state of|γi⟩,(i=1,2,3,4,5,6,7,8)satisfies

The measurement will collapse the state of|Ψ⟩M1234into one of the following states

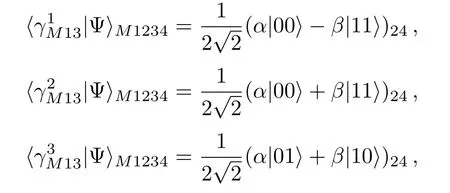
Then Alice sends her measurement result to Charlie and Bob.

(ii)Charlie sends particle 4 through a Hadamard gate,the corresponding states in Eq.(5)can be changed into

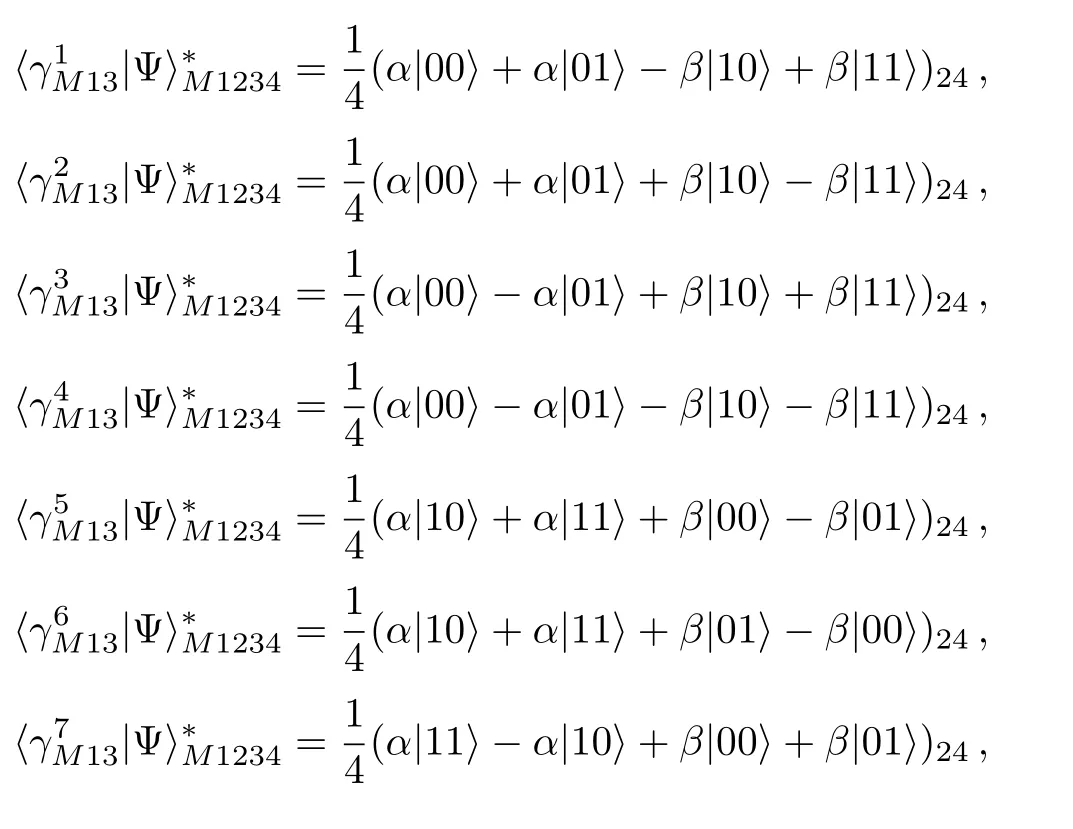
(iii)If Charlie agrees the two parties of communication to complete their teleportation,he performs a single particle measurement on particle 4 with the basis{|0⟩,|1⟩}.Suppose that Alice’s measurement outcome is|γ1⟩M13,Charlie’s measurement will collapse particle 2 into one of the following states

Then Charlie sends his measurement result to Bob.

(iv)Because of the entanglement property,[17−24]Bob can perform an appropriate unitary operator on particle 2 to rebuild the original state|ψ⟩Maccording to Alice’s,Charlie’s measurement results.The corresponding relationship between the measurement results and Bob’s unitary transformations is in Table 1.

Table 1 The relationship between Alice’s,Charlie’s measurement outcomes,and Bob’s operation.

3 Quantum Multi-Proxy Blind Signature Scheme

In our scheme,four participants are defined as follows.

(i)Alice:the massage owner;(ii)Uj:one member of proxy signers(j=1,2,...,t);(iii)Charlie:the original signer;(iv)Bob:the verifier.

The detailed procedure of our scheme can be described as follows.

3.1 Initial Phase

(i)Alice shares secret key KABwith Bob,KAUj(j=1,2,...,t)with signer Uj,respectively. In addition,Bob establishes secret key KBCwith Charlie,KBUjwith Uj(j=1,2,...,t).These distribution tasks can be fulfilled via QKD protocols,which have been proved unconditionally security.[25−28]

(ii)Ujprepares Q(Q≫n)EPR pairs such that

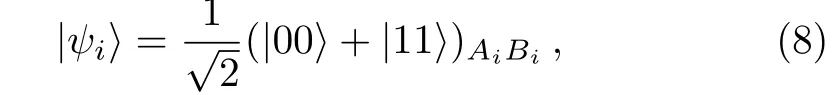
where the superscripts Aiand Biindicate the i-th of two entangled particles.And in each EPR pair,Ujsends particle Aito Alice,while he keeps particle Bi.In addition,Charlie generates TN(TN≫tn)four-qubit Cluster states as showed in Eq.(1)to be the quantum channel.He sends particle 2 to Bob,(1,3)to Ujwhile leaving the last one 4 to himself.The schematic of transmission on the i-th particles is shown in Fig.2.

(iii)To guarantee the security of the quantum channel,Charlie and Ujarrange eavesdropping checks.On the one hand,Charlie chooses TN-tn groups of particle 4 randomly,remembers the positions and performs a measurement with the basis{|0⟩,|1⟩},then Charlie publishes the positions.According to Charlie’s published positions,Ujperforms measurement on the particles(1,3)with the basis{|00⟩,|01⟩,|10⟩,|11⟩},Bob performs measurement on the particle 2 with the basis{|0⟩,|1⟩}.After that,Charlie,Ujand Bob all declare their measurement outcomes.Here,the declared order of them should be random.If their measurement outcomes satisfy the relationship in Table 2 or error rate is less than the threshold value,the quantum channel is safe.Otherwise,they give up this process.On the other hand,Ujalso arranges eavesdropping check by randomly choosing Q-n EPR pairs to ensure the safety of the quantum channel between Ujand Alice.This process is similar to the above mentioned,we do not repeat the details.

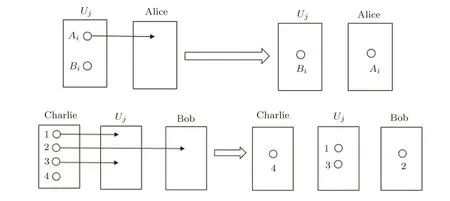
Fig.2 Schematic of transmission on the i-th particles.

Table 2 The relationship between Charlie’s,Uj’s,and Bob’s measurement results.

3.2 Blind the Message Phase

(i)Alice transforms her message into an n-bit message string m={m(1),m(2),...,m(n)}={m(i),i=1,2,...,n},where m(i)∈{0,1}.

(ii)Alice measures her particle sequence according to message m.If m(i)=0,she measures particle Aiwith the basis{|0⟩,|1⟩}.Otherwise,she measures under the basis{|+⟩,|−⟩}.The measurement results can be denoted as m′={m′(1),m′(2),...,m′(n)}={m′(i),i=1,2,...,n},where m′(i) ∈ {|0⟩,|1⟩,|+⟩,|−⟩}and Alice transforms the measurement results into classical binary sequence M={M(1),M(2),...,M(n)}={M(i),i=1,2,...,n},where M(i)∈{00,01,10,11}.The measuring and encoding rules for quantum states are shown in Table 3.Now,message m(n-bit)could be blinded as M(2n-bit).

Table 3 The measuring and encoding rules for quantum states.

(iii)Alice gets the secret message M′by encrypting M with one-time pad and key KAB,we have

Alice sends M′to Bob.

3.3 Authorizing and Signing Phase

We choose a proxy signer Ujon behalf of all proxy signers to complete this signature.

(i)In order to distinguish every proxy signers,Alice generates a unique serial SN,and transforms it to a quantum state sequence⟩in the basisThen she encryptswith key KAUj,and sends the secret state to Ujvia a quantum channel.

(ii) After Ujreceived EKAUj,he decrypts it to gain⟩. Ujperforms a von Neumann measurement on particle Biand particles(1,3),he gains βUj=by combining the measurement results and|SNj⟩,now βUjis Uj’s proxy signature of the blinded message M.Then Ujencrypts βUjwith key KBUjto get the message SUj=EKBUj(βUj),he sends it to Bob and also sends βUjto Charlie as his proxy request.

(iii)After receiving Uj’s proxy request βUj,Charlie will help Ujand Bob to complete their teleportation if he agrees Ujto sign the message. Charlie operates a Hadamard gate on particle 4 and then he measures particle 4 with the basis,and he combines the measurement result β(i)4withto get

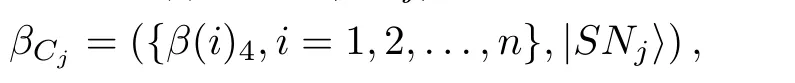
where β(i)4∈.Then he encrypts βCjwith key KBCto get the message SCj=EKBC(βCj),he sends it to Bob.If Charlie does not agree Ujto sign the message,he terminates this teleportation.

3.4 Verifying Phase

(i)Bob decrypts M′to acquire the message M.

(ii)Bob gets βUjand βCjby using KBUjand KBCto decrypt SUjand SCjrespectively.Then Bob performs a proper unitary operator on particle 2 to rebuild the unknown state.In Table 1,we show the relationship between Uj’s Charlie’s measurement results and Bob’s unitary transformation(we replace Alice’s measurement results by Uj’s).

(iii)Bob encodes particle 2 to get a two bits classical string c(j)by using the similar strategy as shown in Subsec.3.2.If c(j)=M,this signature is valid,otherwise,he rejects it.

(iv) Bob collects{(SUj,SCj),j=1,2,...,t},Then according to Subsec.3.2,he gets the message{c(j),j=1,2,...,t}. If c(j)=M (j= 1,2,...,t),Bob will ensure this signature and get the final signature S ={βU1,βU2,...,βUt},otherwise,he terminates the signature.

4 Security Analysis and Discussion

In this section,we will prove that this scheme satisfies the properties of blindness,undeniability,and unforgeability.

4.1 Message’s Blindness

According to Subsec.3.2,the message m has been transformed into m′={m′(1),m′(2),...,m′(n)},where each m′(i) ∈ {|0⟩,.If Ujattempts to get the message m,the only way is to perform measurements.However,he has no idea of Alice’s measurement basis of particle Ai,which means Ujcan not acquire m′and m.Therefore,each proxy signers can not know the content of the message m when he signs it.This means the message is blind for proxy signers.

4.2 Impossibility of Denial

In this scheme,we prove that Charlie can not deny his delegation and Ujcan not disavow his signature.According to Step 2 in Subsec.3.2,Bob decrypts messages SCj=EKBC(βCj)with keys KBCcan get Charlie’s authorization βCj.Similarly,Bob can get Uj’s proxy request and his serial number⟩.All keys are distributed via QKD protocols,which have been proved unconditionally and all messages are sent through the secure quantum channel.Therefore,Charlie can not deny his delegation and Ujcan not disavow his signature.

4.3 Impossibility of Forgery

In the following,we will show that our scheme is secure against the forgery of both internal attacker and outsider attacker.First of all,we demonstrate that it is impossible for the dishonest participants to forge message and signature.Suppose Bob is dishonest and he attempts to forge message or signature,according to Subsec.3.2,Bob can not obtain particle Ai,he has no idea of Alice’s measurement basis.It means that Bob can not get the true signature.If Bob randomly uses basisorhe will obtain the correct results at a probability 1/2n,and this probability will vanish to zero if n is large enough.Therefore,the dishonest inner attacker can not forge message and signature.Secondly,we indicate that it is impossible for the outsider attacker Eve to forge signature.Eve can forge signature successfully unless he has the secret key KBUj.However,the security of the shared key KBUjis guaranteed by unconditionally secure QKD protocols.That is,Eve’s forgery can be avoided.

5 Conclusion

In this paper,we propose a quantum multi-proxy blind signature scheme,which uses entangled four-qubit Cluster state as quantum channel.The security of our scheme is guaranteed by the quantum one-time pad and quantum key distribution,which is different from the previous signature schemes in classical cryptography.In addition,different from some existing quantum signature schemes,our scheme has some advantages.Firstly,our scheme is based on entangled four-qubit Cluster state,which needs less resource rather than the quantum signature proposed in Refs.[29–30].Secondly,differing from the quantum blind signature scheme,[31]our scheme has arranged eavesdropping checks to ensure the security.Thirdly,our scheme has a stronger security because of the cluster state’s maximum connectedness and persistency of entanglement.Fourthly,our scheme adopts von Neumann measurement and single particle measurement,which are easy to implement with current technologies and experimental conditions.However,the received state’s fidelity may reduce because of the experimental environment,and this will be a question to be studied further.

[1]P.Shor,SIAM J.Comput.26(1997)1484.

[2]L.K.Grover,arXiv:quant-ph/9605043.

[3]I.L.Chuang,D.Gottesman,arXiv:quant-ph/0105032.

[4]H.Buhrman,R.Cleve,J.Watrous,et al.,Phys.Rev.Lett.87(2001)167902.

[5]H.Buhrman,C.Crepeau,D.Gottesman,et al.,Authentication of Quantum Massages,IEEE Comput.Soc.Press,Canada(2002).

[6]X.J.Wen,Y.Tian,L.P.Ji,and X.M.Niu,Phys.Scr.81(2010)055001.

[7]Y.Tian,H.Chen,S.F.Ji,et al.,Opt.Quant.Electron.46(2014)769.

[8]M.Mambo,K.Usada,and E.Okamoto,IEICE Trans.Fuan.Electr.79(1996)1338.

[9]J.X.Zhou,Y.J.Zhou,X.X.Niu,and Y.X.Yang,Sci.China Ser.G.54(2011)1828.

[10]G.B.Xu,Int.J.Theor.Phys.54(2015)2605.

[11]Y.Y.Yang,S.C.Xie,and J.Z.Zhang,Int.J.Theor.Phys.56(2017)2293.

[12]C.Zeng,J.Z.Zhang,and S.C.Xie,Int.J.Theor.Phys.56(2017)1762.

[13]D.Chaum,Lect.Notes.Comput.Sc.15(1983)199.

[14]T.Y.Wang and Q.Y.Wen,Chin.Phys.B 19(2010)66.

[15]A.X.Shao,J.Z.Zhang,and S.C.Xie,Int.J.Theor.Phys.55(2016)5216.

[16]W.Guo,J.Z.Zhang,Y.P.Li,et al.,Int.J.Theor.Phys.55(2016)3524.

[17]J.S.Bell,Physica 1(1964)195.

[18]N.Gisin,Phys.Lett.A 154(1991)201.

[19]S.Popescu and D.Rohrlich,Phys.Lett.A 166(2016)293.

[20]R.Chaves,Phys.Rev.Lett.116(2016)010402.

[21]D.Rosset,C.Branciard,T.J.Barnea,et al.,Phys.Rev.Lett.116(2016)010403.

[22]N.Gisin,Q.Mei,A.Tavakoli,et al.,Phys.Rev.A 96(2017)020304(R).

[23]M.X.Luo,Phys.Rev.Lett.120(2018)140402.

[24]M.J.Hu,Z.Y.Zhou,X.M.Hu,et al.,arXiv:quantph/1609.01863.

[25]P.Shor and J.Preskill,Phys.Rev.Lett.85(2000)441.

[26]D.Mayers,J.Assoc.:Comput.Math.48(2001)351.

[27]H.K.Lo,J.Phys.A:Math.Gen.34(2012)6957.

[28]H.Inamon,N.Lutkenhaus,and D.Mayers,Eur.Phys.J.D.41(2007)599.

[29]H.J.Cao,Y.Y.Zhu,and P.F.Li,Int.J.Theor.Phys.53(2014)419.

[30]H.J.Cao,Y.F.Yu,Q.Song,and L.X.Gao,Int.J.Theor.Phys.54(2015)1325.

[31]L.Fan,Int.J.Theor.Phys.55(2016)1558.