Effect of Nonlinear Convection on Stratified Flow of Third Grade Fluid with Revised Fourier-Fick Relations

M.Waqas,M.Ijaz Khan,T.Hayat,,2and A.Alsaedi2Department of Mathematics,Quaid-I-Azam University,Islamabad 44000,Pakistan

2Nonlinear Analysis and Applied Mathematics(NAAM)Research Group,Department of Mathematics,Faculty of Science,King Abdulaziz University,P.O.Box 80257,Jeddah 21589,Saudi Arabia

1 Introduction

The dynamics of nonlinear liquids present an extraordinary challenge to mathematicians,physicists and engineers in view of the fact that nonlinearity can exhibit itself via several manners.The straightforward approach in which viscoelastic liquids are categorized is the approach provided by Truesdell and Noll[1]and Rivlin and Ericksen[2]exhibiting constitutive expressions regarding stress tensor,which comprises total derivative and velocity gradient symmetric part.Several analyses about non-Newtonian liquid flows have been elaborated owing to their technological importance and stimulating mathematical characteristics exhibited through governing flow expressions. A discussion involving salient characteristics of several fluid models(integral,rate)can be consulted through Huilgol,[3]Schowalter,[4]and Rajagopal.[5]The motivation towards such models stalks mainly from reality that constitutive expressions whether we account second or third grade liquids are established on the first principles basis and different from other“phenomenological”models[6]there are no variables to modify.Undoubtedly,second-grade liquid model yields normal stress aspects.However this model is incapable to elaborate shear(thinning,thickening)phenomena. For such intention we adopted third-grade liquid model,which effectively describes shear(thinning,thickening)phenomena.Few analyses comprising this model can be referred through the investigations(Refs.[7–10])and numerous analyses therein.

Regarding the improvement of science and technology,we are continuously in search for a scheme with a view to deliver industrial stuffs with less time and excellent quality.In view of such fact,science has achieved extraordinary improvement in numerous arenas.Fluid mechanics is amongst such sciences in which excellent improvement is made recently.The characteristics of liquid flow field towards moving surface fascinated several researcher considerations,so that comprehensive researches were reported.The scrutiny of liquid flow via moving surface finds it utilizations in hot rolling,polymer extrusion,casting and plastic or drawing films etc.Crane[11]initiated the flow analysis bounded by moving surface.The analysis elaborated by Crane[11]is extended by several researchers via distinct physical characteristics and geometries(detail can be seen through Refs.[12–20]).

Heat conduction aspect via revised Fourier approach can be observed in several situations like microelectronic devices self heating,nano and micro scales in space and time,laser pulses utilized for strengthening semiconductors,small variations in temperature,oscillatory boundary conditions involving heat flux,heat conduction in biological tissues and absolute zero temperatures.[21−22]Revised Fourier approach is utilized by several researchers ever since the innovative analyses addressed by Cattaneo[23]and Christov.[24]Straughan[25]described gravity on viscous liquid considering revised Fourier relation of heat diffusion.Analysis of revised Fourier relation in nonlinear viscous liquid flow under gravitation and heat sink/source is communicated by Kumar et al.[26]Waqas et al.[27−28]visualized thermal dependence conductivity and revised Fourier relation impacts on stretched flow of Burgers and Eyring-Powell materials.Hayat et al.[29]formulated vis-coelastic nanoliquid flow utilizing improved Fourier-Fick relations.Simultaneous features of revised Fourier relation and thermal dependence conductivity in Oldroyd-B liquid flow are discussed by Khan et al.[30]

The prime intention here is to elaborate simultaneous features of revised Fourier-Fick heat-mass diffusion relations in nonlinear convection flow of non-Newtonian(third-grade)liquid by stretched sheet having varying thickness.Aspects of thermal dependence conductivity and double stratification are further considered in this work.Computations of solutions are performed via homotopic theory.[31−40]The outcomes of presented analysis are displayed and discussed.

2 Formulation

Let us formulate nonlinear convection and thermal dependence conductivity characteristics in an incompressible doubly stratified stagnant point third-grade liquid flow bounded by stretching surface having varying thickness.The novel approaches regarding modification in energy and concentration expressions have been introduced simultaneously.Whole analysis is elaborated by neglecting viscous dissipation and thermal radiation aspects.We thus have the following governing expressions:[10]

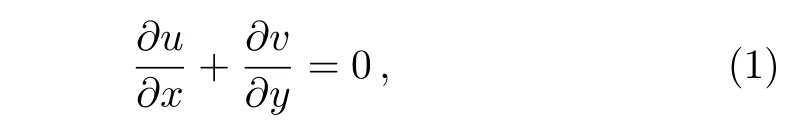
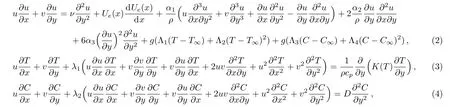
with conditions[10]

Note that(u,v)illustrate liquid velocities in(horizontal,vertical)directions respectively,ν the kinematic viscosity,Uethe free stream velocity,ρ the liquid density,(α1,α2,α3)the material parameters,g the gravitational acceleration,(Λ1,Λ2)the(linear,nonlinear)thermal expansion coefficients,(Λ3,Λ4)the(linear,nonlinear)solutal expansion coefficients,(Tw,T∞)the variable( fluid,ambient fluid)temperatures,(Cw,C∞)the variable( fluid,ambient fluid)concentrations,(T0,C0)the reference(temperature,concentration),D the mass diffusion,(b,c1,c2,d1,d2)are the dimensional constants,n the velocity power index,cpthe specific heat,A1the small variable with respect to surface adequately thin,(Uw(x),Ue(x))the nonlinear(stretching,free-stream)velocities,(U0,U∞)the reference velocities and(λ1,λ2)the(heat,mass) flux relaxation times.Mathematical form of thermal dependence conductivity factor(K(T))is:[10]

in whichthe small variable,which identifies the characteristic of temperature for thermal dependence conductivity,K∞the ambient liquid conductivity and∆T=Tw−T0.

Employing:[10]

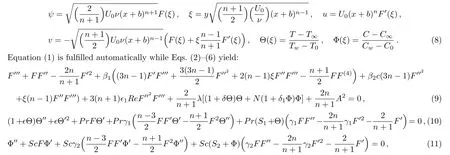
where prime indicates differentiation with respect to ξ.Utilizing F(ξ)=f(ξ− α)=f(η), Θ(ξ)= θ(ξ− α)= θ(η),Φ(ξ)= ϕ(ξ− α)= ϕ(η),Eqs.(9)–(14)yield

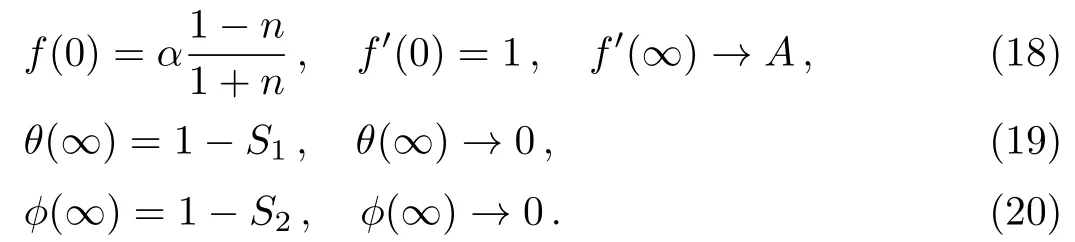
Here β1(= α1U0(x+b)n−1/µ),β2(= α2U0(x+b)n−1/µ),and1(= α3U0(x+b)n−1/µ)are the material parameters of third-grade fluid,λ(= Grx/)the mixed convection or local buoyancy parameter,Grx(= gΛ1×(Tw− T0)(x+b)3/ν2)the thermal Grashof number,δ(= Λ2(Tw−T0)/Λ1)the nonlinear thermal convection parameter,N=(/Grx)the ratio of concentration to thermal buoyancy forces,

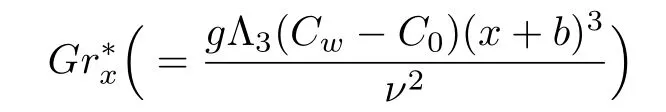
the solutal Grashof number,δ1(= Λ4(Cw−C0)/Λ3)the nonlinear solutal convection parameter,A(=U∞/U0)the ratio of velocities,Pr(=µcp/K)the Prandtl number,γ1(= λ1U0(x+b)n−1)and γ2(= λ2U0(x+b)n−1)the thermal/solutal relaxation factors respectively,S1(=c2/c1)and S2(=d2/d1)the thermal/solutal stratified variables and

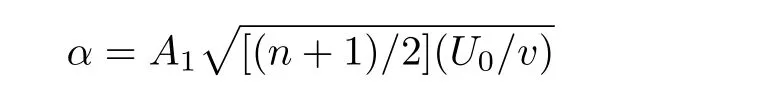
the wall thickness parameter.The coefficient of skin friction(Cf)is defined as:[10]

where τwrepresents the surface shear stress given below

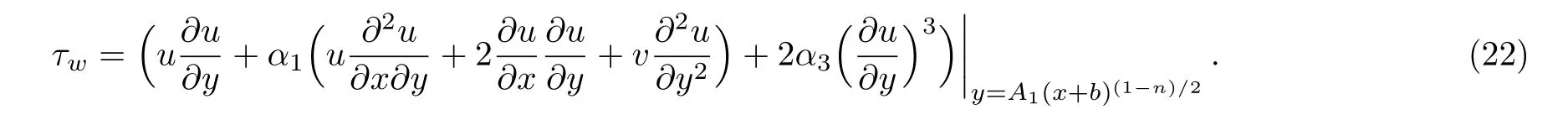
In dimensionless variables we have

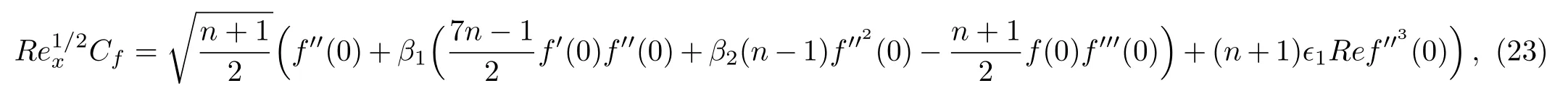
where Rex=(Uw/ν)(x+b)signifies Reynolds number.

3 Convergence Analysis

The variables(f,θ,ϕ)are involved in the construction of convergent series solutions by homotopic scheme.These variables adjust and control convergence region regarding series solutions.We elaborated-curves in Fig.1 for 16-th order approximation. Flat portions of these curves help to achieve admissible values of(f,θ,ϕ).From Fig.1 we found−0.82≤f≤ −0.35,−1.1≤θ≤ −0.25 and−1.0≤ϕ≤ −0.20 with n=0.8,λ =S1= β1=0.2,β2= δ=A= δ1=0.1,γ2=0.4,Re= γ1= α =0.3,=S2=N=0.5,Sc=1.5,and Pr=1.0.Table 1 elaborates convergence analysis numerically.Here it is clear from this table that Eqs.(15)–(17)converge at 35-th order approximation respectively.

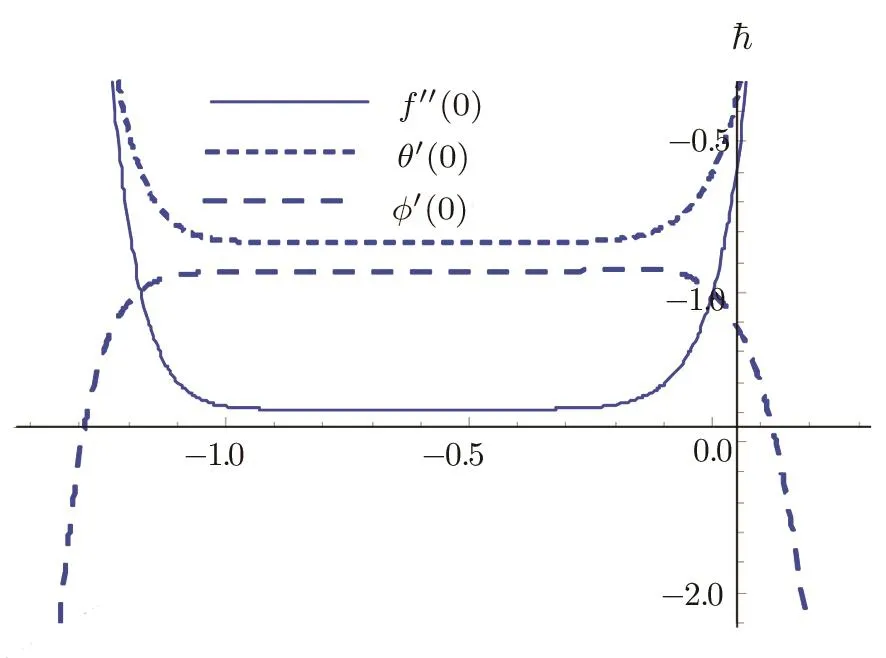
Fig.1 -curve for f,θ,and ϕ.

Table 1 Convergence of series solutions for different order of approximations when n=0.8,λ=S1= β1=0.2,β2= δ=A= δ1=0.1,γ2=0.4,Re= γ1= α =0.3,=S2=N=0.5,Sc=1.5,and Pr=1.0.

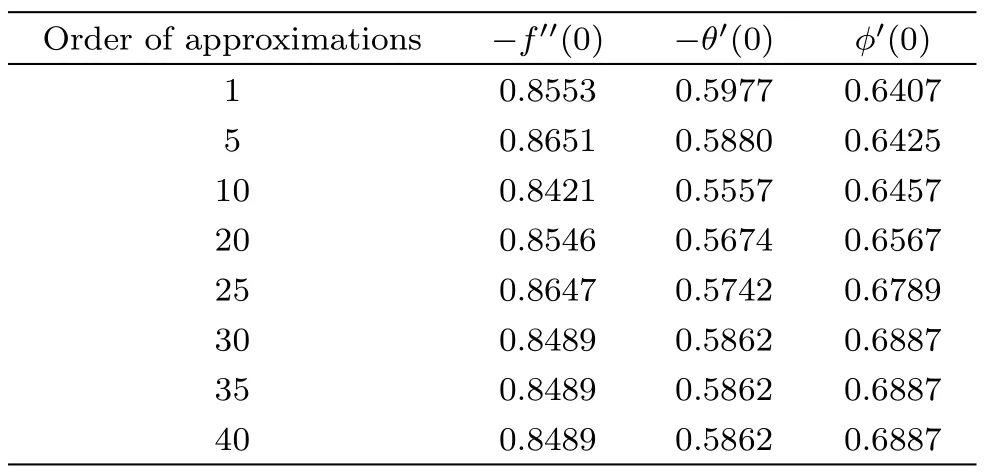
Table 1 Convergence of series solutions for different order of approximations when n=0.8,λ=S1= β1=0.2,β2= δ=A= δ1=0.1,γ2=0.4,Re= γ1= α =0.3,=S2=N=0.5,Sc=1.5,and Pr=1.0.

Order of approximations −f′′(0) −θ′(0) ϕ′(0)0.8553 0.5977 0.6407 5 0.8651 0.5880 0.6425 10 0.8421 0.5557 0.6457 20 0.8546 0.5674 0.6567 25 0.8647 0.5742 0.6789 30 0.8489 0.5862 0.6887 35 0.8489 0.5862 0.6887 40 0.8489 0.5862 0.6887 1

4 Discussion

Characteristics of sundry variables such as λ,δ,,Pr,γ1,S1,Sc,S2,and γ2on velocity(f′),temperature(θ)and concentration(ϕ)are elaborated in detail.Figures 2–10 are constructed for such interest.Influences of λ and δ on f′are illustrated in Figs.2 and 3.Larger estimation of δ and λ exhibit a rise in f′and corresponding thickness of momentum boundary layer.In fact buoyancy force is enhanced for larger λ,which boosts f′(see Fig.2).Furthermore,the difference between(wall,ambient)temperatures increment when δ is increased.Therefore f′is noticed increasing function of δ(see Fig.3).Figure 4 communicates θ variation for.Here thermal layer and θ rise for higher estimation of.Liquid thermal conductivity rises whenis enhanced Consequently additional amount of heat is exchanged from surface to liquid and accordingly θ is boosted.Prandtl(Pr)number impact on θ is revealed in Fig.5.Higher estimation of Pr yields lower diffusivity,which reduces θ and related thickness layer.

Fig.2 f′characteristics for λ.

Figure 6 elaborates γ1characteristics versus θ.It is observed that larger estimation of γ1results in θ reduction.In fact non-conducting behavior is noticed when γ1is incremented.Besides,θ enhances only when γ =0 whereas it diminishes for γ >0.The role of S1against θ is presented in Fig.7.It is investigated that both thermal layer and θ are diminished for higher S1.Due to a rise in S1,the temperature difference(between sheet,ambient fluid)is dwindled that yields lower θ and thinner thickness of thermal layer.

Fig.3 f′characteristics for δ.

Fig.4 θ characteristics for .

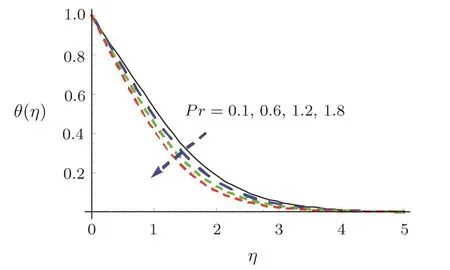
Fig.5 θ characteristics for Pr.

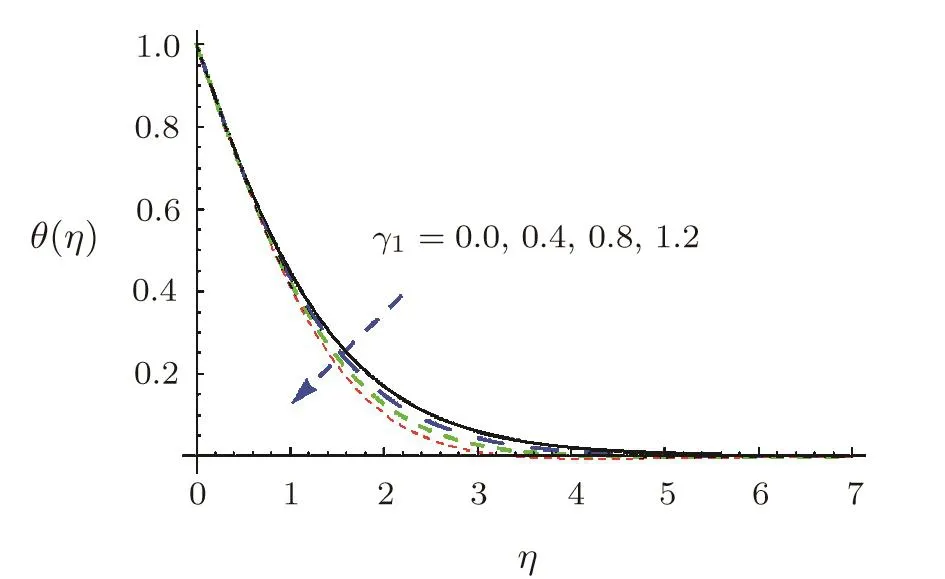
Fig.6 θ characteristics for γ1.

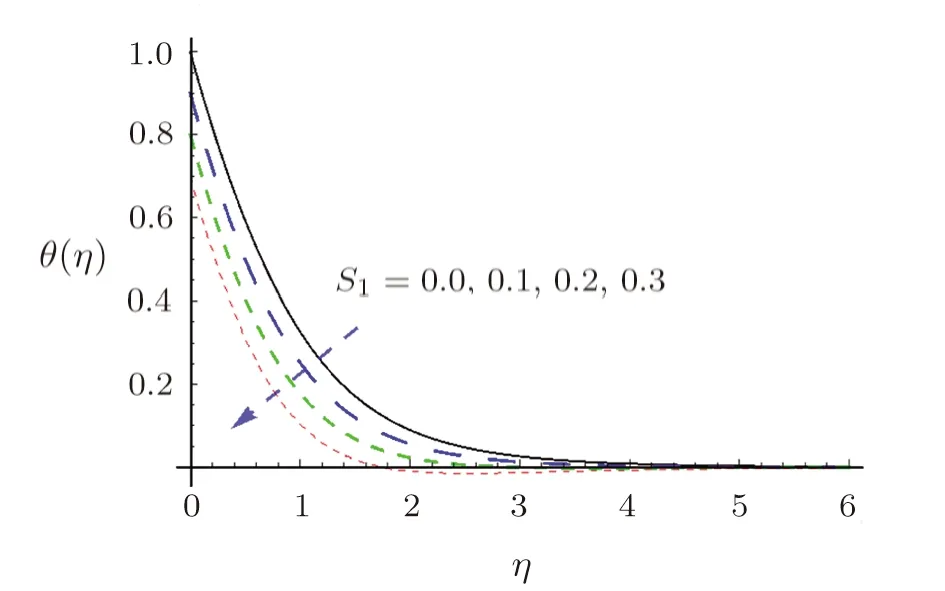
Fig.7 θ characteristics for S1.

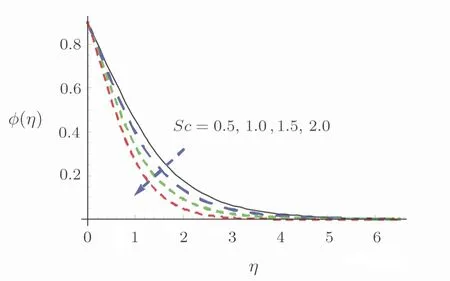
Fig.8 ϕ characteristics for Sc.

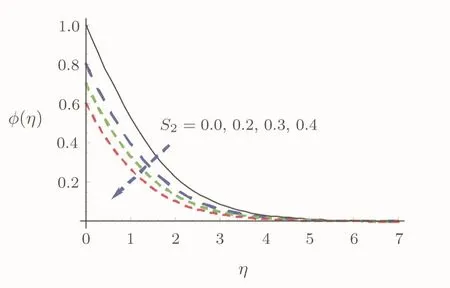
Fig.9 ϕ characteristics for S2.

Figure 8 addresses Sc behavior on ϕ.Here ϕ diminishes for higher Sc.In fact Sc involves Brownian diffusivity thus an increment in Sc provides less Brownian diffusivity.Thus ϕ decays.Analysis for the characteristics of S2and γ2is described via Figs.9 and 10.Clearly an increment in S2and γ2shows reduction in concentration layer and ϕ.

Fig.10 ϕ characteristics for γ2.

Table 2 elaborates analysis of surface drag force for β1,β2,A and α.This table certifies that surface drag force increments via larger β1,β2and α whereas it decays when A is taken large.

Table 2 Skin friction(Cf)for distinct values of parameters β1, β2,A,and α when n=0.8,N=0.5,λ =S1=0.2,δ= δ1=0.1,γ2=0.4,Re= γ1=0.3,=S2=0.5,Sc=1.5,and Pr=1.0.

Table 2 Skin friction(Cf)for distinct values of parameters β1, β2,A,and α when n=0.8,N=0.5,λ =S1=0.2,δ= δ1=0.1,γ2=0.4,Re= γ1=0.3,=S2=0.5,Sc=1.5,and Pr=1.0.

β1 β2 A α −CfRe1/2x 0.0 0.1 0.2 0.3 0.1356 0.2 0.2368 0.4 0.2563 0.1 0.0 0.3658 0.2 0.4568 0.4 0.6599 0.1 0.0 0.5687 0.2 0.4368 0.4 0.3659 0.1 0.0 0.2896 0.2 0.4862 0.4 0.7989

5 Conclusions

The presented research leads to the following conclusions:

(i) Velocity(f′)increments when λ and δ are enhanced.

(ii)Temperature(θ)is noted higher for=0 when compared with>0.

(iii)Larger S1and S2result in θ and ϕ reduction.

(iv)Prandtl(Pr)and Schmidt(Sc)numbers correspond to a decay in thermal and solutal layers.

(v) Surface drag force decays when A is enhanced whereas it enhances via larger β1, β2and α.

(vi)Revised Fourier-Fick situations can be achieved by setting γ1= γ2=0.

[1]C.Truesdell and W.Noll,The Non-Linear Field Theories of Mechanics,(2nd ed.)Springer,New York(1992).

[2]R.S.Rivlin and J.L.Ericksen,J.Ration.Mech.Anal.4(1955)323.

[3]R.R.Huilgol,Continuum Mechanics of Viscoelastic Liquids,Hindustan Publishing Corporation,Delhi(1975).

[4]W.R.Schowalter,Mechanics of Non-Newtonian Fluids,Oxford University Press,Pergamon Press,Oxford(1978).

[5]K.R.Rajagopal,Mechanics of Non-Newtonian Fluids,Recent Developments in Theorectical Fluid Mechanics,Pitman Research Notes in Mathematical Series,eds.G.P.Gladi and J.Necas,Vol.291,Longman Science Technology,Marlow(1993)pp.129-162.

[6]M.Reiner,Rheology S.Flügge(ed.),Handbuch der Physik,Vol.VI,Springer,Berlin(1958).

[7]S.O.Adesanya and J.A.Falade,Alex.Eng.J.54(2015)615.

[8]T.Hayat,M.Waqas,S.A.Shehzad,and A.Alsaedi,J.Mol.Liq.223(2016)853.

[9]T.Hayat,M.I.Khan,M.Waqas,et al.,Chin.J.Chem.Eng.25(2017)257.

[10]M.Zubair,M.Waqas,T.Hayat,et al.,Results Phys.(2017)DOI:10.1016/j.rinp.2017.12.010.

[11]L.J.Crane,Z.Angew.Math.Phys.21(1970)645.

[12]S.Nadeem,R.U.Haq,and C.Lee,Sci.Iran.19(2012)1150.

[13]T.Hayat,M.Waqas,S.A.Shehzad,and A.Alsaedi,Sci.Iran.Trans.B Mech.Eng.21(2014)682.

[14]R.U.Haq,S.Nadeem,Z.H.Khan,and N.F.M.Noor,Phys.B 457(2015)40.

[15]M.Waqas,M.Farooq,M.I.Khan,et al.,Int.J.Heat Mass Transfer 102(2016)766.

[16]T.Hayat,M.Waqas,S.A.Shehzad,and A.Alsaedi,Pram.J.Phys.86(2016)3.

[17]P.Besthapu,R.U.Haq,S.Bandari,and Q.M.Al-Mdallal,J.Taiwan Inst.Chem.Eng.71(2017)307.

[18]G.K.Ramesh,B.J.Gireesha,S.A.Shehzad,and F.M Abbasi,Commun.Theor.Phys.68(2017)91.

[19]M.Waqas,M.I.Khan,T.Hayat,and A.Alsaedi,Comp.Methods Appl.Mech.Eng.324(2017)640.

[20]T.Hayat,M.Waqas,S.A.Shehzad,and A.Alsaedi,J.Aerospace Eng.30(2017)04016077.

[21]J.Ghazanfarian and A.Abbassi,Int.J.Heat Mass Transfer 52(2009)3706.

[22]F.Xu,K.A.Seffen,and T.J.Lu,Int.J.Heat Mass Transfer 51(2008)2237.

[23]C.Cattaneo,Mat.Fis.Univ.Modena Reggio Emilia 3(1948)83.

[24]C.I.Christov,Mech.Res.Commun.36(2009)481.

[25]B.Straughan,Int.J.Heat Mass Transfer 53(2010)95.

[26]K.A.Kumar,J.V.R.Reddy,V.Sugunamma,and N.Sandeep,Alex.Eng.(2016)DOI:10.1016/j.aej.2016.11.013.

[27]M.Waqas,T.Hayat,M.Farooq,et al.,J.Mol.Liq.220(2016)642.

[28]M.Waqas,M.Ijaz Khan,T.Hayat,et al.,Chin.J.Phys.55(2017)729.

[29]T.Hayat,S.Qayyum,S.A.Shehzad,and A.Alsaedi,Results Phys.8(2018)489.

[30]W.A.Khan,M.Irfan,and M.Khan,Results Phys.7(2017)3583.

[31]S.J.Liao,Chapman and Hall,CRC Press,Boca Raton(2003).

[32]M.Turkyilmazoglu,Int.J.Mech.Sci.52(2010)1735.

[33]S.A.Shehzad,M.Waqas,A.Alsaedi and T.Hayat,J.Appl.Fluid Mech.9(2016)1437.

[34]T.Hayat,M.Waqas,S.A.Shehzad,and A.Alsaedi,J.Mol.Liq.223(2016)566.

[35]T.Hayat,M.Waqas,S.A.Shehzad,and A.Alsaedi,Eur.Phys.J.Plus 131(2016)253.

[36]R.U.Haq,Z.Hamouch,S.T.Hussain,and T.Mekkaoui,Int.J.Hydrogen Energy 42(2017)15925.

[37]N.Muhammad,S.Nadeem,and R.U.Haq,Results Phys.7(2017)854.

[38]M.Ramzan,M.Bilal,S.Kanwal,and J.D.Chung,Commun.Theor.Phys.67(2017)723.

[39]T.Hayat,A.Aziz,T.Muhammad,and A.Alsaedi,Commun.Theor.Phys.68(2017)387.

[40]M.Waqas,T.Hayat,S.A.Shehzad,and A.Alsaedi,Physica B 529(2018)33.