传感器工作时长约束及辐射控制的调度方法

乔成林，段修生，单甘霖，王俭臣

(1.陆军工程大学，河北 石家庄 050003;2.中国人民解放军驻西北工业大学军事代表室，陕西 西安 710065)

0 引言

多传感器系统能从不同角度获取目标信息，为了满足对多目标的观测要求，需要管理调度多传感器资源[1-2]。传统的传感器调度研究中，通常以传感器最大化目标收益(如跟踪误差最小、信息增益最大)。然而，有源传感器(如雷达)在持续获得量测时会向外发射电磁波，容易暴露自身位置，降低己方生存能力。为此，文献[3-5]研究了目标跟踪中辐射控制问题，其以跟踪精度为需求，当不满足精度需求时，雷达开机获得量测，否则不开机，以降低系统辐射。然而，该方法并没有对雷达辐射进行量化，实际上不同时刻的雷达辐射代价是不同的。随后，文献[6]在传感器多模式调度中将辐射代价量化为固定值，并采用加权系数构建基于辐射代价的目标函数，实现对智能目标的精确跟踪。相比于固定辐射代价，文献[7-9]提出采用截获概率的熵实时量化辐射代价更具实用性。但是，使用截获概率衡量辐射代价需要提前获知敌方目标窗函数参数，这在实际中往往难以获得[8]。

此外在上述调度方法中，为了追求最大目标收益，大多数调度方法中均存在传感器频繁切换问题，这不仅加快了传感器能量耗损，更严重影响了分配方案的稳定性[10]。文献[11]在卫星调度中提出设置交接次数阈值来避免频繁切换，但容易错失最优调度方案。文献[12-13]通过在目标优化函数中引入切换代价以减缓频繁切换，但是切换代价的设置往往由经验值决定，可操作性不强。进一步，文献[14]研究了连续时间域传感器调度问题，寻求最大切换次数约束下最优调度序列，由于不考虑最小工作时间，其最优调度序列中仍存在频繁切换的缺陷。针对上述问题，提出传感器工作时长约束及辐射控制的调度方法。

1 系统模型及目标优化函数

引入辐射度影响(Emission Level Impact， ELI)[15]量化传感器辐射风险，并将目标跟踪和辐射控制过程建立为统一的部分可观马尔可夫决策过程(Partially Observable Markov Decision Process, POMDP)。

1.1 系统模型

1) 传感器调度动作

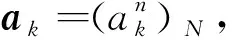
2) 系统状态及状态转移

系统状态Sk由目标运动状态Xk和传感器ELI状态Ek组成，即

(1)

目标状态按照目标状态转移方程转移到下一时刻，即

Xk+1=FkXk+1+Γk·vk

(2)

式(2)中，F、Γ和v分别为状态转移矩阵、噪声增益矩阵以及零均值高斯噪声。对于近似匀速运动(NCV，Nearly Constant Velocity)模型[7]，则

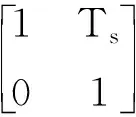
(3)

式(3)中，I3表示3×3单位矩阵，符号⊗表示克罗内克积。

将传感器ELI状态量化为有限状态集合{1，…，Ns}，集合中每个值代表相应的ELI状态真值[14]。则当调度传感器n跟踪目标时，可采用一个受控的状态转移矩阵描述其ELI状态变化，即

(4)

3) 系统观测及观测矩阵

系统观测Zk由目标状态观测ZXk和瞬间观测威胁度ZEk组成，则

(5)

式(5)中，ZXk和ZEk分别表示传感器跟踪目标时获得的量测值及其对应的瞬间观测威胁度。

在调度动作作用下，假设传感器n获得目标量测值。对于有源传感器(如雷达)，其量测值由斜距离r、方位角θ及高低角φ组成，即

ZXk=hn(Xk)+w

(6)

式(6)中,hn(Xk)=[rk，θk，φk]T;

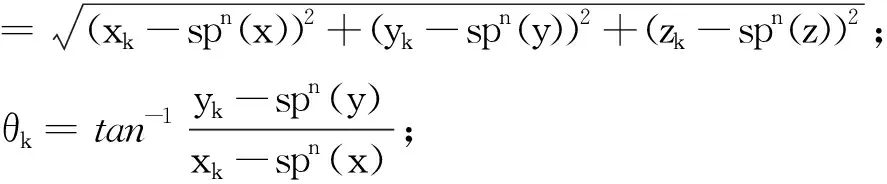
同理，将瞬间观测威胁度量化为有限状态集合{1，…，Ms}，集合中每个值对应真实的瞬间威胁度。考虑到瞬间观测威胁度与真实瞬间威胁度的关系[14]，可用一组观测矩阵来表示，即

(7)

1.2 目标优化函数

考虑目标跟踪任务需求及传感器应用实际，不能为了最大限度的控制辐射，频繁切换传感器。为此，需要研究工作时长约束下传感器调度问题，具体描述为

假设存在N个传感器资源ψ1，…，ψN，其工作时长约束为τ1，…，τN。为了不失一般性，假设在k时刻传感器β已经连续工作了τβ(τβ是其工作时长约束)，则在下一时刻需要决策是否需要切换至其他传感器。根据工作时长约束，k+1时刻可以继续调度当前传感器，也可以切换到其他传感器n(n≠β)，但是一旦切换就必须至少工作τn。进一步，以N=3(传感器ψ1,ψ2,ψ3)，τ1=τ2=3，τ3=4为例，不妨设截止k时刻传感器ψ1已经工作了3，则k+1时刻需要决策在第λ(1，2，3，…)切换，其对应的调度方案可以是ψ2ψ2ψ2,ψ3ψ3ψ3ψ3,ψ1ψ2ψ2ψ2等。很明显，由于工作时长约束，存在无穷多种调度方案，比较所有可能的调度方案是不切实际的。此外，考虑到越往后时刻的信息对当前时刻的决策影响越小，为了简化分析，并倾向于继续调度当前传感器，进一步减少切换次数，调度策略制定如下

不妨设，k时刻传感器β已经连续工作了τβ：

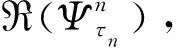
具体目标优化函数描述为

s.t.ρt≤ρth，t=k+1，…，k+τn

(8)

式(8)中，ρt为t时刻目标跟踪精度，ρth为跟踪任务需求对应的精度阈值。

进一步分析可知，当τn=1时即为传统的无工作时长约束调度模型，这里是对τn>1场景的推广。

2 传感器工作时长约束及辐射控制的调度方法

由于系统状态不能完全可观，为了保持对目标运动状态和ELI状态的持续更新，引入信念状态bk=[bXk，bEk]T，其中bXk为目标信念状态，bEk为ELI信念状态[17]。则根据所有历史信息及初始状态，得

(9)

式(9)中，X0和pX0为目标初始状态及状态分布，E0和pE0为ELI初始状态及状态分布。

2.1 目标跟踪精度预测

依据贝叶斯滤波原理，目标信念状态更新包括预测和更新两个阶段，即预测阶段为

(10)

更新阶段为

(11)

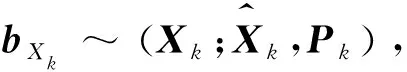
1) 初始化

目标信念状态中获取状态均值和方差

(12)

式(12)中，μXk和σXk分别是bXk的期望值和标准差。

2) 时间更新

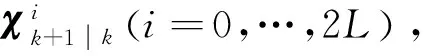
(13)

(14)

式(13)、式(14)中，L为状态维数，w=[w0，…，w2L]T为权重向量。

3) 量测更新

(15)

Pk+1=Pk+1|k-Kk+1|kPzz(Kk+1|k)T

(16)

其中，Pk+1|k、Sk+1和Ck+1分别是预测协方差，新息协方差和互协方差[18]。

4) 更新目标信念状态，预测跟踪精度

(17)

(18)

2.2 系统单步与多步辐射代价

依据HMM滤波器，若已知k+1瞬间观测威胁度，则可以获知k+1时刻ELI信念状态[19]。以调度传感器n为例，其ELI信念状态更新为

(19)

式(19)中，lk+1为k+1时刻瞬间观测威胁度。

进一步，得

(20)

式(20)中，1为Ns维单位向量，符号⊙表示Hadamard积。

定义k+1时刻传感器n跟踪目标的单步辐射代价为其ELI信念状态的期望，即

(21)

虽然k时刻无法准确获知k+1时刻的瞬间观测威胁度，但是可以依据当前时刻ELI信念状态推导其分布概率，即

(22)

结合式(4)和式(7)，得

(23)

因此，式(21)转化为

(24)

则k+1时刻系统的单步辐射代价为

(25)

进一步，k+h时刻系统的单步辐射代价为

(26)

则系统多步辐射代价为

(27)

式(27)中，ΨH为长度为H的传感器调度序列。

2.3 调度方法流程

对于多传感器系统，不妨设k时刻传感器β已经工作了τβ(τβ是其工作时长约束)，则结合目标跟踪精度预测及传感器辐射代价预测，式(8)目标函数转化为

s.t.ρt≤ρth，t=k+1，…，k+τn

(28)

因此，工作时长约束及辐射控制下传感器调度方法流程为:

步骤1)初始阶段。得到目标的初始状态X0和初始协方差矩阵P0；

步骤2)预测跟踪精度。由2.1节预测跟踪目标跟踪精度；

步骤3)计算辐射代价。由式(25)和(27)计算传感器单步及多步辐射代价；

步骤4)传感器调度。根据式(28)获得跟踪精度需求及工作时长约束下，具有最小辐射代价的传感器；如果不存在可行解，则调度具有最小跟踪误差的传感器；

步骤5)重复步骤2)～4)，直至任务结束。

3 仿真实验

考虑一个包含N=3个有源传感器系统，在三维空间内跟踪单个目标。目标初始位置为(8，50，5)km，传感器位置分别为(0，0)km、(10，10)km和(0，10)km。考虑实际应用，采样间隔设为1 s，仿真总时间为60 s。仿真结果均为500次蒙特卡洛实验的平均。

此外，ELI状态量化为{1，2，3}(1代表较小值，2代表中等值，3代表较大值)，瞬间观测威胁度量化为{1，2，3}(1代表小增量，2代表中增量，3代表高增量)。为了不失一般性，假定传感器3的测量噪声最小，但其ELI状态更易处于较高值。传感器其他性能参数具体设置为:

σr1=σr2=50 m，

σθ1=σθ2=σφ1=σφ2=0.005 rad,

σr3=10 m，σθ3=0.001 rad，σφ3=0.001 rad,

仿真中，以工作时长约束τ1=τ3=3、τ2=4为例。同时，为了验证本文调度方法的有效性，采用以下两种常用调度策略进行对比：1)最近调度策略(Closest Scheduling Policy,CSP)[7]；2)无工作时长约束调度策略(Scheduling Policy without Timestep Constraint,SPTC)。

3.1 不同阈值下，目标均方根误差对比

图1为不同阈值下，目标均方根误差(Root Mean Square Error,RMSE)对比。如图所示，CSP根据传感器与目标距离调度最近的传感器跟踪目标，不同阈值下其跟踪误差几乎不变，不能满足跟踪任务需求。相比于CSP，SPTC和本文方法均能跟踪跟踪任务需求调度合适的传感器，由图可知，在不同阈值下，SPTC和本文方法的RMSE曲线总体上均在阈值下方。进一步，结合图4可知，初始时刻由于目标误差较大，根据调度策略，其调度跟踪误差最小的传感器以迅速满足任务需求，符合实际应用。

3.2 不同阈值下，辐射代价与ELI值对比

图2和图3分别为不同阈值下，归一化累计辐射代价和归一化累积ELI值对比。由图2和图4可知，由于CSP长时调度易处于高ELI值的传感器(传感器3)，其归一化累计辐射代价较高。而SPTC和本文方法能够自适应的选择满足任务需求且辐射代价小的传感器跟踪目标，其归一化辐射代价要小于CSP。进一步，结合图4可知，相比于SPTC，本文方法以辐射代价稍有上升为代价有效避免了传感器频繁切换问题。此外，对比图2和图3可知，由于实际使用中不能获知准确的ELI，目标函数(28)中的辐射代价设置为其期望值。结合仿真结果可知，辐射代价能够有效地反映出真实的ELI值，验证了目标函数的合理性。因此，本文方法能够在工作时长约束下，有效地控制系统辐射。

3.3 不同策略下，传感器调度序列对比

图4为跟踪精度阈值为100 m时，CSP、SPTC及本文方法的传感器调度序列。由图可知，CSP一直选择最近距离的传感器跟踪目标，而SPTC和本文方法能够根据跟踪任务需求自适应的调度满足要求的传感器跟踪目标。进一步，SPTC为了最大限度的降低系统辐射，频繁的切换传感器，严重不切合实际。相比之下，本文方法结合实际应用，考虑工作时长约束，并根据辐射代价自适应得控制传感器工作时长，避免了频繁切换问题。整个过程中，SPTC共发生了27次切换，而本文方法只有11次切换，平均切换时间间隔为5.5 s，更利于工程实现。

4 结论

本文提出了传感器工作时长约束及辐射控制的调度方法。考虑跟踪任务需求，在传感器工作时长约束下，由传感器辐射代价自适应控制其工作时长。仿真结果验证了方法有效性和合理性，与CSP相比，本文方法能够在满足跟踪任务需求下，获得更小的辐射代价；与无工作时长约束策略相比，本文方法在辐射代价稍有上升条件下，显著降低了切换次数，避免了频繁切换问题，增强了系统稳定性与实用性。

参考文献:

[1]Nayebi-Astaneh A，Pariz N，Naghibi-Sistani M. Adaptive node scheduling under accuracy constraint for wireless sensor nodes with multiple bearings-only sensing units[J]. IEEE Trans. on Aerospace and Electronic Systems，2015，51(2)：1547-1557.

[2]Kim Y，Bang H. Airborne multisensor management for multitarget tracking[C]//Proc. of the IEEE International Conference on Unmanned Aircraft Systems. us: IEEE, 2015：751-756.

[3]吴巍，王国宏，双炜，等. 多机载平台多目标跟踪与辐射控制[J]. 系统工程与电子技术，2012，34(3)：495-501.

[4]陈兴凯，韩壮志，封吉平,等. 基于跟踪精度的火控雷达网间歇开机控制策略[J]. 探测与控制学报，2013 35(5)：74-78.

[5]吴卫华，江晶，高岚. 机载雷达辅助无源传感器对杂波环境下机动目标跟踪[J]. 控制与决策，2015，30(2)：277-282.

[6]杨海燕，尤政，王琳. 基于传感器多模式调度的智能目标跟踪算法[J]. 控制理论与应用，2012，29(9)：1186-1192.

[7]Zhang Z，Shan G. UTS‐based foresight optimization of sensor scheduling for low interception risk tracking[J]. International Journal of Adaptive Control and Signal Processing，2014，28(10)：921-931.

[8]Zhang Z，Shan G. Non-myopic sensor scheduling to track multiple reactive targets[J]. IET Signal Processing，2015，9(1)：37-47.

[9]张子宁，单甘霖，段修生. 基于部分可观马氏决策过程的多平台主被动传感器调度[J]. 电子学报，2014，42(10)：2104-2109.

[10]罗开平，姜维，李一军. 传感器管理述评[J]. 电子学报，2010，38(8)：1900-1907.

[11]程洪玮，王博，安玮. 一种基于信息决策树的低轨星座传感器调度方法[J]. 电子学报，2010，38(11)：2630-2634.

[12]Krishnamurthy V，Djonin D V. Optimal Threshold Policies for Multivariate POMDP in Radar Resource Management[J]. IEEE Transactions on Signal Processing，2009，57(10)：3954-3969.

[13]姜维，李一军. 天基预警调度方法研究[J]. 系统工程理论与实践，2012，32(9)：2065-2077.

[14]Wu X，Zhang K，Sun C. Optimal scheduling of multiple sensors in continuous time[J]. ISA Transactions，2014，53(3)：793-801.

[15]Krishnamurthy V. Emission management for low probability intercept sensors in network centric warfare[J]. Aerospace and Electronic Systems，IEEE Transactions on，2005，41(1)：133-151.

[16]Wu P，Li X，Kong J，et al. Heterogeneous multiple sensors joint tracking of maneuvering target in clutter[J]. Sensors，2015，15(7)：17350-17365.

[17]Charlish A，Hoffmann F. Anticipation in cognitive radar using stochastic control[C]//Proc. of the IEEE on Radar Conference，us: IEEE, 2015：1692-1697.

[18]Roy A，Mitra D. Unscented kalman filter based multitarget tracking algorithms for airborne surveillance application[J]. Journal of Guidance，Control，and Dynamics，2016：1949-1966.

[19]Krishnamuthy V，Evans R J. Hidden markov model multiarm bandits：A methodology for beam scheduling in multitarget tracking[J]. IEEE Transactions on Signal Processing，2001，49(12)：2893-2908.