基于无迹卡尔曼滤波和权值优化的改进粒子滤波算法

冉星浩，陶建锋，杨春晓

(1.空军工程大学防空反导学院，陕西 西安 710051;2.中国人民解放军93567部队，河北 保定 074100)

0 引言

相比于传统的卡尔曼滤波算法，粒子滤波算法不受线性化误差或高斯噪声假定的限制，适用于非线性、非高斯系统。近年来，随着计算机计算能力的不断提高，以Monte-Carlo模拟为特点的粒子滤波(Particle filtering)算法逐渐成为解决非线性、非高斯系统估计问题的研究热点，广泛应用于雷达、声纳、红外、导航制导、计算机视觉、金融统计和目标跟踪等领域[1-6]。

1993年，Gordon等人提出了自举粒子滤波算法[7](Bookskrap Particle Filter)，通过在递推过程中引入重采样[8]的思想以克服粒子退化现象[9]，奠定了粒子滤波算法的基础。但是，在标准粒子滤波算法中基于先验分布的重要性函数与真实后验概率密度函数[10]存在较大偏差，因此，Merwe等人提出一种无迹粒子滤波[11](Unscented Particle Filtering，UPF)，该算法使用无迹卡尔曼滤波(Unscented KalmanFiltering，UKF)算法产生重要性密度函数，一定程度上提高了滤波精度，然而粒子集在重采样过程中不可避免会产生样本贫化[12]问题。本文针对重要性密度函数的的合理选取，粒子退化现象以及样本贫化等问题，在UPF算法的基础上，结合权值优化[13]思想，提出了新的改进粒子滤波算法，(Improved Unscented Particle Filtering，IMUPF)。

1 算法原理

1.1 标准粒子滤波算法

粒子滤波是一种基于蒙特卡洛方法和递推贝叶斯估计的统计滤波方法，它依据大数定理采用蒙特卡罗方法来求解贝叶斯估计中的积分运算[14]。其基本思想是：首先依据系统状态向量的经验条件分布在状态空间产生一组随机样本的集合，称为粒子，并计算每个粒子权值，然后利用样本和其对应的权系数来近似表示目标状态的后验概率密度函数，从而利用近似的后验概率密度函数实现对目标状态的估计。

假设系统方程与状态方程如下所示：

xk=f(xk-1)+wk-1

(1)

zk=h(xk)+vk-1

(2)

式(1)，式(2)中，xk为系统的状态变量，zk为系统的量测变量，wk为系统噪声，vk为过程噪声，且分别为独立同分布的噪声序列；映射f(·)，h(·)分别为系统状态转移函数和量测函数。

后验概率密度为：

(3)

在标准粒子滤波中，为了求解方便，一般取重要性密度函数为先验概率分布，即：

(4)

标准粒子滤波算法描述如下：

1) 初始化：k=0

2) 重要性采样：k=1，2，…，N

a)从建议分布函数中随机抽取N个粒子：

(5)

权值更新公式为：

(6)

b)更新粒子权值并对权值进行归一化：

(7)

归一化：

(8)

3) 重采样：

4) 状态估计：对各个粒子加权估计系统状态及误差

(9)

(10)

5) 令k=k+1，返回步骤2)。

1.2 UPF算法

UPF算法具体步骤如下：

1) 初始化：k=0。

(11)

(12)

(13)

(14)

2)k=1，2，…

①重要性采样：i=1，2，…，N，使用UKF算法更新粒子

a) 选取粒子：

(15)

b) 时间更新

(16)

(17)

(18)

(19)

(20)

c) 量测更新：

(21)

(22)

(23)

(24)

(25)

采样粒子：

(26)

式(26)中，N(·)表示高斯函数。

令：

(27)

计算权重：

(28)

并归一化权值。

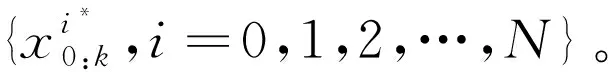
③输出融合结果：

(29)

2 改进UPF算法

在UPF算法中，引入重采样过程，抑制粒子退化现象。重采样技术是为了解决重要性权值可能偏差很大的问题，一旦偏差过大，无效样本数会增多，过多的无效样本会降低蒙特卡洛方法的效率，重采样是一个减少无效样本、增加有效样本的有效方法，它允许舍弃“坏”样本，复制“好”样本从而适应目标的动态变化。常用的重采样有随机重采样、多项式重采样、残差重采样、分层重采样、系统重采样。上述重采样方法由于简单重复复制大权值粒子同时轻易丢弃了小权值粒子，损失了粒子多样性，引发粒子贫化甚至枯竭的问题[15]。

针对UPF算法重采样导致的粒子贫化问题，本文采用了一种重要性权值优化重采样思想，通过引入一个影响因子来优化粒子的重要性权重，加强了重采样后粒子的有效性和多样性，有效地提高了UPF算法的性能。

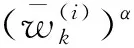
(30)

这样每个粒子的权值得到了重新调整，权值小的粒子在优化后权值得到提高，相反权值大的粒子权值会降低，改善了粒子集的多样性。下面验证该方法的有效性：

(31)

(32)

(33)

同理：

结合UPF算法和上述权值优化算法思想，改进算法的具体步骤总结如下：

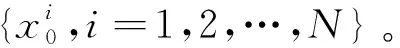
3) 权值计算：通过式(28)计算权值并进行归一化。

4) 权值优化：引入一个影响因子α来优化粒子的重要性权重，并进行归一化。

(34)

6) 状态估计：

(35)

7) 返回步骤2)。

3 仿真结果与分析

为了验证改进算法优越性，本文分别用标准PF、UPF和IMUPF算法分别对非线性、非高斯的系统进行状态估计，其状态方程和观测方程分别为：

x(k)=1+sin(0.04πk)+0.5xk-1+uk-1

(36)

(37)

(38)

式中，量测噪声vk服从Gamma分布γ(3，2)，系统噪声uk是方差为1×10-5的高斯白噪声。

仿真参数设置：粒子数N=100，仿真时间步长T=60，时间间隔Δt=1，初始状态方差intVar=0.75，初始位置x0=1，得到状态估计仿真结果如图1-图3所示。

图1和图2分别是PF算法，UPF算法和IMUPF算法的跟踪效果对比图和估计误差对比图。从这两幅图可以看出IMUPF算法相比较PF算法和UPF算法而言，更加接近真实轨迹，同时误差也更小。这是因为用UKF算法产生的重要性函数比用先验分布产生的重要性函数更加接近真实的后验分布，同时采用权值优化的重采样方法增加了粒子多样性，改善了样本贫化问题。

为了能够进一步验证本文改进算法的优越性，分别对以上三种算法进行10次蒙特卡罗实验，得到各个时刻的均方根误差(Root Mean Square Error，RMSE)如图3所示。这里的RMSE引用文献[12]中的RMSE公式，即

(39)

分别对三种算法求其运行时间以及所有时刻的均方根误差求平均，可以得到平均RMSE，进行多次实验，得到各算法的平均RMSE如表1所示。

表1 三种算法的平均RMSE

Tab.1 The average RMSE of three algorithms

算法平均RMSE运行时间/sPF0.791 10.312 4UPF0.079 90.502 8IMUPF0.031 00.515 1

从图3以及表1我们可以看出标准PF算法的平均RMSE为0.791 1，运行时间为0.312 4；UPF算法的平均RMSE为0.079 9，运行时间为0.502 8；IMUPF算法的平均RMSE为0.031 0，运行时间为0.515 1，可以算出与标准PF算法相比IMUPF算法在运行时间增加64.88%的同时，均方根误差降低了96.08%;与UPF算法相比IMUPF算法在运行时间增加2.44%的同时，均方根误差降低了61.20%，所以改进算法大大提高了滤波精度。

4 结论

本文结合无迹卡尔曼滤波和权值优化的方法，提出了基于无迹卡尔曼滤波和权值优化的改进粒子滤波算法。该算法通过无迹卡尔曼滤波产生重要性密度函数，解决了重要性函数的选取问题，然后通过引入一个影响因子对粒子权值进行优化，增加了粒子的多样性，解决了样本贫化问题。仿真结果表明，该算法的跟踪轨迹与真实轨迹最为接近，其平均RMSE最小，与标准粒子滤波，无迹粒子滤波等算法相比，具有更强的抗噪能力和更好的跟踪性能，下一步需要在提高算法实时性上深入研究。

参考文献:

[1]吴兆平，朱凯然，苏涛，等.采用改进粒子滤波的雷达扩展目标检测前跟踪[J].西安电子科技大学学报，2011，38(2)：99-104.

[2]李浩，王润亮，彭华.粒子滤波盲均衡译码联合算法[J].西安电子科技大学学报，2013，40(1)：123-128.

[3]胡洪涛，敬忠良，李安平，等.非高斯条件下基于粒子滤波的目标跟踪[J].上海交通大学学报，2004，38(12)：1996-1999.

[4]周明，涂宏斌.一种基于改进粒子滤波的多目标检测与跟踪方法[J].华东交通大学学报，2016，33(2)：121-126.

[5]孙景乐，唐林波，赵保军，等.基于瑞丽分布的粒子滤波跟踪算法[J].电子信息学报，2013，35(4)：763-769.

[6]Zou J Y，Wu C H，Ma T G.Heterogeneous Integrated Beam-switching/Retrodirective Array Using Synthesized Transmission Lines[J].IEEE Transactions on Microwave Theory and Techniques，2013，61(8)：3128-3139.

[7]Gordon N J，Salmond D J，Smith A. A novel approach to nonlinear and non-Gaussian Bayesian state estimation[C]//IEEE Proceeding，1993，140：107-113.

[8]LIU J S，CHEN R.Sequential monte carlo methods for dynamic systems[J].J.of the American Statistical Association，1995，90(2)：567-576.

[9]DOUCET A，GODSILL S.On sequential monte carlo sampling methods for bayesian filtering[R].Cambridge：University of Cambridge，1998.

[10]TAI S.Cloud service engineering[C]//Proc of the 18th IEEE International Workshops on Enabling Technologies：Infrastructures for Collaborative Enterprises.Washington DC：IEEE Computer Society，2009：3-4.

[11]Wan E A，Van Der Merwe R.The unscented kalam filter for nonlinear estimation[C]//Proceeding of the IEEE 2000 Adaptive Systems for Signal Processing，Communications，and Control Symposium.Piscataway：IEEE，2000：153-158.

[12]ARULAMPPALAM M S，MASKELLS，GORDON N，et al.A tutorial on particle filter for online nonlinear/non gaussssian bayesian tracking[J].IEEE Trans.on Signal Processing，2002，50(2)：174-188.

[13]杜正聪，辛强，邓寻，等.基于权值优化的粒子滤波算法研究[J].重庆师范大学学报，2015，32(3)：124-129.

[14]朱志宇.粒子滤波算法及其应用[M].北京：科学出版社，2010.

[15]朱军.基于权值优化的粒子滤波算法研究及其在目标跟踪中的应用[D].安徽：安徽建筑大学，2014：1-61.