基于波束域的多测量矢量欠定系统正则化聚焦求解算法

房云飞，王洪雁，裴炳南

(大连大学信息工程学院，辽宁 大连 116622)

0 引言

波达方向(Direction of Arrival，DOA)估计是阵列信号处理中的重要研究内容之一，在雷达、声纳、移动通信、无线传感器网络等领域得到广泛应用[1-2]。自20世纪60年代以来，研究者们提出了大量有效的DOA估计算法，主要有最小方差谱估计法[3](Minimum Variance Distortionless Response，MVDR)和以多重信号分类(Multiple Signal Classification，MUSIC)为代表的子空间算法[4]。上述DOA估计算法皆基于如下假设：信源不相关，快拍数量足够多，且信噪比(Signal Noise Ratio，SNR)足够大。若快拍数量少、信噪比较低，这些算法性能将明显下降，尤其在信源相关情况下，由于信号协方差矩阵会出现秩亏现象，导致这些算法估计精确度更低。

近年来，信号处理领域中提出的压缩感知(Compressing Sensing，CS)理论[5-6]吸引了研究人员的极大关注，已广泛应用于图像处理[7]和无线通信[1]等诸多领域。针对阵列DOA估计运算量较大的问题，基于CS理论，Liang G等人利用目标空域稀疏特性，提出一种稀疏恢复l1-SVD算法[8]。在已知信源数量条件下，即使信源信号相关，该算法都将得到DOA的高精度估计。然而，在没有信源数量先验信息情况下，该算法性能会明显下降。针对此问题，Cotter把多快拍和匹配追踪算法(MP)相结合，提高了DOA估计性能[9]。为进一步提高DOA估计的分辨率和精确度，Gorodnitsky和Rao提出把欠定系统聚焦求解(Focal Underdetermined System Solver，FOCUSS)算法和lp惩罚函数结合对DOA进行估计，其中p<1[10-11]。此外，为了避免接收信号协方差矩阵求解产生奇异值的缺陷，文献[12]提出一种通过迭代和阈值转换的DOA估计方法。文献[13]则采用奇异值分解欠定系统聚焦求解(Singular Value Decomposition-regularized Multi-vectors Focal Undetermined System Solver，SVD-RMFOCUSS)算法实现DOA高分辨率估计，然而由于此算法基于阵元域，导致SVD-RMFOCUSS算法计算复杂度比较高。文献[14]基于波束域采用Dantzig Selector算法实现DOA估计，减少了算法的计算复杂度。然而，Dantzig Selector算法的DOA估计谱峰较宽，不利于角度高分辨。针对上述问题，本文提出基于波束域的多测量矢量欠定系统正则化聚焦求解(Beamspace-regularized Multi-vectors Focal Undetermined System Solver，BS-RMFOCUSS)算法。

1 稀疏波达方向角估计模型

(1)

式(1)中，a(θk)表示来波方向θk的M×1维阵列导向矢量，且a(θk)=[1，exp(-jα)，…，exp(-j(M-1)α)]T，α=2πdsin(θk)/λ表示均匀线性阵列平面内各阵元之间的第k条信号到达此阵元时的相移，w(t)表示叠加在阵列接收回波中的M×1维噪声矢量。

为了便于推导，式(1)可重新表示为：

x(t)=As(t)+w(t)

(2)

式(2)中，A=[a(θ1)，a(θ2)，…，a(θk)]是阵列流型矩阵，s(t)=[s1(t)，s2(t)，…，sk(t)]T是K×1维信号矢量。

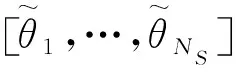
由上述分析，可得过完备阵列流型矩阵，即过完备稀疏基，则每个可能来波信号对应导向矢量可表示为：

(3)

定义NS×1信号稀疏矢量：

(4)

基于式(3)和式(4)，式(2)可重新表示为：

x(t)=Ψz(t)+w(t)

(5)

由此，将接收信号x(t)投影至投影测量矩阵Φ，可得：

y(t)=Φx(t)=ΦΨz(t)+Φw(t)

(6)

对于多次快拍(数量为N)，上式可表示为：

Y=ΦX=ΦΨΖ+ΦW=ΘZ+ΦW

(7)

由式(7)可知，上述算法基于阵元域建立接收信号模型，在采用稀疏重构算法实现DOA估计的同时，也会导致算法计算量大、估计稳定性差等问题，实施性比较差。

2 波束域RMFOCUSS重构算法

为进一步降低DOA估计算法的运算复杂度，本文提出一种波束域欠定系统聚焦求解(BS-RMFOCUSS)算法，通过波束转换矩阵T将阵列接收到的信号从阵元域映射到波束域，即：

yB(t)=THΦx(t)=ΦBΨz(t)+ΦBw(t)

(8)

式(8)中，T为M×NB的波束形成矩阵，满足THT=INB，NB为波束数量，ΦB=THΦ。由文献[15]可知，T可表示为：

(9)

式(9)中m为波束形成矩阵的始端点。

对于多次快拍，式重写为：

YB(t)=THΦX(t)=ΦBΨZ(t)+ΦBW(t)=

ΘZ(t)+ΦBW(t)

(10)

式(10)中，Θ=ΦBΨ表示波束域下的感知矩阵。

由上式知，基于压缩感知的波束域DOA估计优化问题可表示如下：

minJ(p，q)(Z) s.t.‖YB-ΘΖ‖F≤ε

(11)

上述优化问题可采用拉格朗日乘子法进行求解[11]，即：

(12)

式(12)中，γ为平衡估计误差与稀疏性的参数，可根据修正l曲线法[16]预先选取最优γ值，其在一定信噪比范围内变化较小。

式(12)可通过DOA近似重构算法实现求解，本文通过RMFOCUSS算法对优化模型(12)中的稀疏信号z进行估计，具体实现步骤描述如下：

3) 信号矢量Zk+1=Wk+1Qk+1；

由上可得信号z的近似稀疏逼近，进一步可得BS-RMFOCUSS算法的谱估计公式：

P(θi)=‖z(i，∶)‖2

(13)

3 实验仿真及分析

基于非相干、相干信号及远近目标模型，本节通过与传统的CAPON、MUSIC算法进行对比，验证BS-RMFOCUSS算法有效性。仿真条件如下：均匀线性阵列阵元个数M=12，信号快拍数为N=50；从-180°到180°以1°为间隔将目标角度空间划分为361，即网格划分数量为361；考虑到目标角度范围，波束数取NB=8。目标信号采用零均值、方差为1的复高斯随机信号，目标信号与加性复高斯噪声互不相关。采用均方根误差作为算法性能指标，其中均方根误差定义为：

(14)

实验1考虑两个入射角度分别为10°和15°的非相干信号，信噪比为10 dB，进行20次独立蒙特卡罗实验。图1为采用CAPON算法、MUSIC算法和BS-RMFOCUSS算法的空域谱估计输出对比。从图1可以看出，在两个非相干信号角度间隔为5°时，各算法均能正确分辨出两个目标角度，且具有相近的估计性能，需要注意的是，本文提出的BS-RMFOCUSS算法比CAPON算法、MUSIC算法空域谱估计输出具有更窄的主峰和更低的旁瓣，因而具有更好的角度分辨力及估计精度。

实验2考虑两个入射角度分别为10°和12°的邻近非相干信号，信噪比为10 dB，进行20次独立蒙特卡罗实验。图2为采用CAPON算法、MUSIC算法和BS-RMFOCUSS算法的空域谱估计输出对比。从图2可以看出，在两个邻近非相干信号角度间隔为2°时，BS-RMFOCUSS算法能够对邻近目标实现有效估计，且具有较窄的主瓣，而CAPON算法和MUSIC算法无法分辨两个邻近信号。图2表明，在波束域下，BS-RMFOCUSS算法同样具有更高的分辨能力。

实验3考虑两个入射角度分别为10°和15°的非相干信号，信噪比为-10 dB，进行20次独立蒙特卡罗实验。图3为采用CAPON算法、MUSIC算法和BS-RMFOCUSS算法的空域谱估计输出对比。从图3可以看出，在低信噪比条件下，仅有BS-RMFOCUSS算法能够成功分辨两个信号，而CAPON算法和MUSIC算法只呈现出一个误估的谱峰，无法分辨两个信号。图3表明基于波束域的BS-RMFOCUSS算法在低信噪比的情况下同样具有较好的分辨能力。

实验4考虑两个入射角度分别为10°和15°的非相干信号，信噪比为10 dB，进行20次独立蒙特卡罗实验。图4为采用CAPON算法、MUSIC算法和BS-RMFOCUSS算法的DOA估计均方根误差随信噪比变化关系曲线。从图4可以看出，BS-RMFOCUSS算法在低信噪比条件下的均方根误差曲线略低于CAPON和MUSIC方法，且随着信噪比的增大，各算法的均方根误差曲线均趋向于平稳状态。

实验5考虑两个入射角度分别为10°和20°的相干信号，信噪比为10 dB，进行20次独立蒙特卡罗实验。图5为采用CAPON算法、MUSIC算法和BS-RMFOCUSS算法的空域谱估计输出对比。从图5可以看出，CAPON算法和MUSIC算法在相干信号情况下，不能对两个相干信号进行精确有效的估计，且两种算法的旁瓣相对较高，而BS-RMFOCUSS算法不仅可分辨两个相干信号，且具有更窄主瓣。图5表明波束域BS-RMFOCUSS算法在信号相干的情况下同样具有较高的角度估计精度和较好的角度分辨能力。

实验6为进一步验证所提算法复杂度优势，本文与基于阵元域的RMFOCUSS算法进行对比。考虑到实际情况，基于阵元域RMFOCUSS算法复杂度近似为O(2MS2+MLS2+M3(M-1)(M-2))，BS-RMFOCUSS算法复杂度近似为O(2MS2+MLS2+2NML+N3(N-1)(N-2))，其中M为阵元数，S为稀疏字典个数，L为快拍数，N为波束数。实验仿真取S=361，L=200，N=8。从图6可以看出，当阵元数量较小时，两种算法的运算复杂度近似相同。但是，随着阵元数量的不断增大，阵元域RMFOCUSS算法的运算复杂度呈指数上升趋势，而本文所提算法在复杂度增长率上远低于阵元域RMFOCUSS算法。由此可知，与基于阵元域的RMFOCUSS算法相比，所提算法具有较低计算复杂度和较好的算法运算性能。

4 结论

本文提出了基于波束域的多测量矢量欠定系统正则化聚焦求解(BS-RMFOCUSS)算法。该算法利用低旁瓣的波束形成器，将目标压缩信号从阵元域映射到波束域，避免了传统DOA估计算法采样数据量大导致较大计算复杂度的问题。仿真结果表明，与传统的Capon及MUSIC算法相比，所提算法在低信噪比及相干信号条件下，具有较好的DOA估计精度；与基于阵元域的RMFOCUSS算法相比，所提算法具有较低计算复杂度。

参考文献:

[1]Alawsh S A，Muqaibel A H，Sharawi M S. DOA estimation in MIMO systems with compressivesensing for future handsets[C]//IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies. Jordan：IEEE，2015：1-6.

[2]Yang X，Chi C K，Zheng Z. Direction-of-arrival estimation of incoherently distributed sources using Bayesian compressive sensing[J]. Iet Radar Sonar Navigation，2015，10(6)：1057-1064.

[3]Capon J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE，1969，57(8)：1408-1418.

[4]Schmidt R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas & Propagation，1986，34(3)：276-280.

[5]Nishimura T，Ogawa Y，Ohgane T. DOA estimation by applying compressed sensing techniques[C]//IEEE International Workshop on Electromagnetics. Japan，Sapporo：IEEE，2014：121-122.

[6]Chen Y，Huang J，He C. High resolution direction-of-arrival estimation based on compressive sensing with noval compression matrix[C]//IEEE International Conference on Signal Processing，Communication and Computing. China，HK：IEEE，2012：764-767.

[7]Romberg J. Imaging via compressive sampling[J]. IEEE Signal Processing Magazine，2008，25(2)：14-20.

[8]Liang G，Han B. New method of DOA estimation in the presence of interference[C]//IEEE International Conference on Electronic Measurement & Instruments. China，Harbin：IEEE，2013：650-654.

[9]Cotter S F. Multiple snapshot matching pursuit for direction of arrival (DOA) estimation [C]//Signal Processing Conference. European: IEEE, 2007:247-251.

[10]Gorodnitsky I F，Rao B D. Sparse signal reconstruction from limited data using FOCUSS：A re-weighted minimum norm algorithm[J]. IEEE Transactions on Signal Processing，1997，45(3)：600-616.

[11]Cotter S F，Rao B D，Engan K，et al. Sparse solutions to linear inverse problems with multiple measurement vectors[J]. IEEE Transactions on Signal Processing，2005，53(7)：2477-2488.

[12]Lei S，Wang H. Direction-of-arrival estimation based on modified Bayesian compressive sensing method[C]//International Conference on Wireless Communications and Signal Processing. China，Hefei：IEEE，2011：1-4.

[13]贺亚鹏，李洪涛，王克让，等. 基于压缩感知的高分辨DOA估计[J]. 宇航学报，2011，32(6)：1344-1349.

[14]Chen Y，Huang J，Han J. A novel beamspace algorithm for direction of arrival based on compressive sensing[C]//International Conference on Signal Processing. China，Beijing：IEEE，2012：394-397.

[15]Donoho D L，Huo X. Uncertainty principles and ideal atomic decomposition[J]. IEEE Transactions on Information Theory，2001，47(7)：2845-2862.

[16]Rao B D，Engan K，Cotter S F，et al. Subset selection in noise based on diversity measure minimization[J]. IEEE Transactions on Signal Processing，2003，51(3)：760-770.