基于预见位姿信息的铰接式车辆LQR-GA路径跟踪控制

孟 宇 汪 钰 顾 青 白国星

(北京科技大学机械工程学院， 北京 100083)

0 引言

铰接式车辆具有中央铰接点连接，前后车体可相对转动的结构特点，在低矮巷道和复杂工况行驶，具有灵活、机动、高效等突出优点。铰接式车辆的路径跟踪是智能矿山领域的研究热点。针对铰接车的路径跟踪控制，赵翾等[1]针对铰接式车辆使用Ackermann公式与指数趋近律设计滑模控制进行路径跟踪，HEMAMI等[2]设计了一种基于误差动力学的路径跟踪控制器，PETROV等[3]在铰接式车辆中应用了线性反馈控制，BIGRAS等[4]提出一种基于线性矩阵不等式的控制框架，RIDLEY等[5]将极点配置方法应用于铰接车中，NAYL等[6]设计了一种采用切换模型的预测控制方案，邵俊恺等[7]提出一种基于强化学习的控制算法。其中文献[2-3]没有给出具体的误差分析，文献[1,4-7]的研究结果中位置偏差有较大超调，最大偏差大于0.5 m。过大的位置偏差可能会导致车辆在狭长、低矮巷道行驶时碰撞巷道壁，且最终稳定跟踪精度也有待提高。实现高精度的稳定路径跟踪控制是保证无人驾驶铰接车安全自主行驶的关键，有必要对其开展深入研究。

线性二次型最优控制(LQR)是一种稳定的控制方法，可利用较小的控制能量使系统状态变量维持在零值附近[8]，且同时可以对不稳定系统进行整定，对于铰接车多自由度运动、且行驶环境噪声信号复杂的情况具有突出优势。为提高铰接式车辆路径跟踪的跟踪精度，本文结合铰接式车辆的运动学和动力学特点，基于其误差动力学模型提出一种基于预见信息的线性二次型最优控制(LQR)方法。拟利用航迹推算方法对铰接车的下一采样时刻进行位姿估计，将预见位姿信息作为控制器的部分输入可有效提高控制对象的反应速度。同时，将利用全局优化算法遗传算法对Q、R矩阵进行优化，获得最优反馈控制率，实现铰接车的精确路径跟踪，并利用Simulink和ADAMS联合仿真验证控制策略的有效性，且在模型样机中进行试验验证。

1 路径跟踪控制策略

1.1 铰接式车辆运动学模型

γ=θf-θr

图1 铰接式车辆模型Fig.1 Articulated vehicle model

由于铰接式车辆行驶速度较低，一般小于28 km/h[10],轮胎变形对行驶影响可忽略不计，假设α=β=0[11]，可得铰接式车辆运动几何关系

(1)

选取前桥中点Pf(Xf,Yf)为整车状态参考点，可以得到整车运动学模型为

(2)

由式(2)可知，通过控制车速和铰接角可以实现对铰接式车辆位姿状态的实时控制。本文所用35 t铰接式车辆模型部分结构参数如表1所示。

表1 铰接式车辆模型基本参数Tab.1 Main parameters of articulated vehicle model

1.2 预见位姿推算模型

在控制中根据车辆当前行驶的位姿状态信息，利用航迹推算技术建立预见位姿状态模型，进行下一时刻采样点位置的位姿估计，在车辆路径跟踪中加入预见信息，可提高路径跟踪控制的反应速度[12]。

铰接式车辆行驶曲线和参数定义示意图如图2所示，曲线A为车辆行驶曲线;前车体中点为P，预见车辆位置点为P′；前后车体转向中心分别为Or、Of;前后车体的航向角分别为θf、θr，转向半径分别为Rf、Rr[13]。

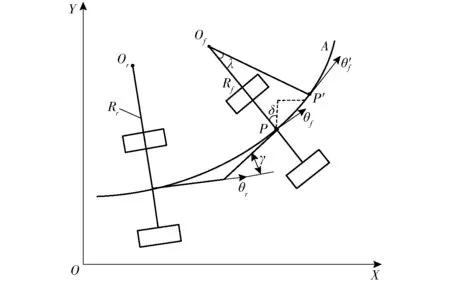
图2 铰接式车辆行驶曲线和参数定义Fig.2 Articulated vehicle modeling configuration

通过铰接车的运动学模型分析，得到前车体航向角变化速度为

(3)

假定采样间隔为Δt，前车体的预见航向角为

(4)

假定车辆逆时针转动为正方向，计算可得前车体的转向半径为

(5)

为区分车辆转动和直线行驶状态，设置车体转动状态量ts，且满足以下条件

(6)

其中，设置的阈值ε通常取值较小，当铰接角γ处在该阈值范围内，认为车体没有转动。如图2所示，车体由P(x,y)点移动到P′(x′,y′)所用时间为Δt，前车体的转向角速度为ωf，则前车体转过角度为

λ=|ωf|Δt

(7)

且由几何关系可得车体移动距离

(8)

可推算下一时刻车辆前车体中点坐标P′(x′,y′)为[13]

(9)

(10)

(11)

式中δ——预见航向角与当前航向角偏差

1.3 误差动力学模型

铰接角和车速是路径跟踪控制的控制变量，本文重点是实现铰接角的实时控制。需要建立合适的偏差量作为控制输入，并能够完整地反映跟踪控制精度。车辆匀速行驶速度为v，根据车辆行驶中的实际路径和理想路径的偏差情况建立的行驶示意图如图3所示[5]。

图3 铰接式车辆行驶示意图Fig.3 Graphical representation of driving of articulated vehicle

偏差定义与分析如下[3]：

(1)位置偏差εd：铰接车参考定位点p与参考轨迹上对应点P(与参考轨迹距离最近)的横向位置差值

(12)

(2)行驶方向偏差εθ：铰接车定位参考点p的航向角(速度方向与车辆坐标系x轴之间的夹角)与参考轨迹上对应点P的航向角(对应点的切线与车辆坐标系x轴之间的夹角)的差值

(13)

(3)曲率偏差εc：铰接车定位参考点p与参考轨迹上对应点P的曲率差值

(14)

整理式(12)～(14)，根据L=Lf+Lr，可得

(15)

铰接式车速较低，且铰接角变化较小，对铰接角速度的变化率通常可以忽略，对式(15)简化，得到铰接车误差动力学方程为

(16)

在恒速运动情况下，铰接车误差动力学模型为单输入的线性时不变模型，通过控制偏差量可实现对车辆铰接角的实时控制。

1.4 转向运动分析与数学建模

铰接车的ADAMS模型仅能反映车辆的运动学和动力学特性，为了使仿真过程符合铰接车的实际转向过程，对铰接车的转向机构进行运动分析和建模。铰接车的转向机构为电机驱动的液压转向系统，将转向系统分为4个环节，并分别针对各个环节建立了比例电磁阀模型、阀芯受力平衡模型、阀控液压缸-负载模型及转向系统运动学摸型，分别推导了电磁阀控制压力与占空比关系、液控力与阀芯位移关系、活塞输出位移与阀芯输入位移关系以及活塞输出位移与车辆铰接角关系，最终确定了电信号即占空比与输出铰接角的关系，并最终获得匀速转向的转向机构数学模型。铰接车转向系统数学仿真模型如图4所示，仿真结果如图5所示，铰接角速度为0.14 rad/s，完全符合实车的转向特性。

图4 转向系统仿真模型Fig.4 Steering system simulation model

图5 转向模型仿真结果Fig.5 Steering model response in simulation

图6 路径跟踪控制系统Fig.6 Path tracking control system

2 路径跟踪控制器

针对以上分析，建立路径跟踪控制系统如图6所示。根据铰接式车辆的运动学模型分析进行速度和铰接角控制来实时控制车辆的行驶位姿状态。由式(16)可看出，在恒速情况下，铰接车的误差动力学模型为线性时不变模型，而铰接车在地下巷道行驶过程中车速较低且很少出现较大幅度的加减速情况，因此本研究中车辆以3 m/s的速度匀速行驶，采用PID速度控制建立速度控制器，使车速维持恒稳，再以恒速条件下的线性时不变的误差动力学模型作为铰接角控制模型。对于铰接角的控制，根据车辆的当前行驶位姿信息进行下一采样点的位姿估计可以得到预见位姿信息，且通过当前行驶状态和预见行驶状态与理想路径的偏差可获得车辆的当前状态跟踪偏差和预见状态跟踪偏差，建立线性时不变的单输入偏差状态方程进行LQR-GA控制，实现理想铰接角输入。通过PID速度控制和LQR-GA铰接角控制实现铰接式车辆车的实时路径跟踪。

2.1 LQR控制器

LQR最优控制可利用较低成本使系统达到预期性能指标，且也可以同时对不稳定系统进行整定，对线性时不变系统的状态反馈控制问题中，往往可取得良好控制效果，已被应用于许多工程和科学领域[14-16]，同时也被运用于众多复杂系统[17-20]。建立线性系统模型为

(17)

式中A——系统状态矩阵，A∈Rn×n

B——输入矩阵，B∈Rn×n

C——输出矩阵，C∈Rp×n

D——状态反馈矩阵，D∈Rp×m

u(t)、X(t)、Y(t)——系统输入量、状态量以及输出量

根据式(17)以及表1中铰接式车辆模型参数可得铰接式车辆的矩阵为

由此，可控可观性分析为

(18)

矩阵均满秩证明该系统具有可控可观性，结合式(16)、(17)，铰接式车辆的LQR控制器模型为线性时不变单输入系统模型为

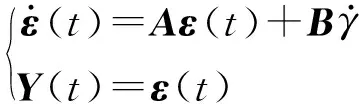
(19)

(20)

式中Q——系统状态量权阵

R——系统控制量权阵

J1反映铰接车偏离平衡状态的程度，J2反映控制能量大小。控制目标是使最优性能指标取得最小值，即以最小的控制能量使路径跟踪偏差达到最小，建立反馈控制率u=-KX(t)，满足K=R-1BTP，建立Riccati方程

ATP+PA+Q-PBR-1BTP=0

(21)

式中P——对称正定矩阵

通过求解最优Q、R矩阵可求得最优反馈控制率，实现理想铰接角输入。路径跟踪控制器的设计如图7所示。

图7 铰接式车辆路径跟踪控制器Fig.7 Articulated vehicle path tracking controller

其中，当前偏差量为当前时刻车辆位姿与理想路径中位姿的偏差，预见偏差量为下一时刻的预见位姿与理想路径位姿的偏差，为避免引入的预见信息量值过大，导致控制过度引起车辆抖振，在控制器中加入柔化操作环节，综合考虑当前偏差量信息和预见的偏差量信息，以提高控制器的稳定性和反应速度，即LQR控制器的最终输入为

ε(t)=aε1(t)+bε2(t)

(22)

其中

式中ε1(t)——当前跟踪偏差矩阵

ε2(t)——预见信息偏差矩阵

a、b——柔化系数

ε(t)——LQR控制器输入

2.2 GA算法优化

遗传算法(GA)是一种用于解决最优化的一种搜索启发式算法，具有良好的全局搜索能力，并且利用其内在并行性，可以方便地进行分布式计算，加快求解速度。

在LQR控制中存在状态量权重矩阵Q和控制能量权重矩阵R的选取两个重要问题，不同的选取结果将直接影响控制效果，在传统优化方法中，Q、R的计算通常会耗费较长时间且多依赖于专家经验[21]。遗传算法作为一种全局优化算法，可对Q、R矩阵进行优化，克服传统LQR控制的缺点，LQR-GA控制在倒立摆控制、复合电力系统和飞行器俯仰控制等[22-24]问题中已取得较大进展。

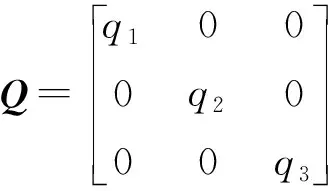
图8 遗传算法流程Fig.8 Block diagram of genetic algorithm scheme

评价函数选择为LQR控制的最优性能指标，当最优性能指标取得最小值时，即可达到最优控制效果。且设置约束条件为

(23)

(1)编码方式

因为二进制编码通常会在目标函数中引入附加的多峰性，使得编码后的目标函数比原始问题更复杂，并且在函数优化和约束优化领域，实数编码比二进制和Gray编码更为有效，实数编码在基因型空间和表现型空间中是一致的，在本文中采用实数编码。

(2)群体取值范围

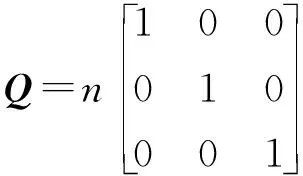
(24)

由于采用无限时间状态调节器的控制系统,其闭环系统是渐进稳定的，n变化范围为1～100，变化间隔为10，系统的闭环极点位置。

表2显示了系统的闭环极点位置与状态反馈增益矩阵K随着n变化的趋势。由闭环极点位置变化可以判断，n>30后继续增大对于主导极点的影响甚微，仅对于系统的辅助极点有一定影响，使其远离虚轴原点,对系统的性能影响不大，因此，n应取较小值，即取n≤30。状态反馈增益矩阵K的变化如表2所示，随着n增大而增大，对于状态变量的变化约束加强。

表2 闭环极点位置及状态反馈矩阵K随n的变化Tab.2 Change of K with n in closed-loop pole position and state feedback matrix

综合以上分析，取n≤30，即群体中个体最大值为30。

(3)交叉方式

采用离散交叉的方式，即选定一个基因位，如选定q1，然后将选定的2个染色体在这个位置之后的基因进行交换。

(4)变异

在任意一个基因位，如选定q1，随机产生2个整数相交换等来进行变异。

(5)参数选取

设定种群数为100，精英数为10，交叉概率为0.4，连续进化代数限制为20，遗传算法迭代终止代数为50，采用随机一致选择、顺序排序。

建立适应度函数为

(25)

自适应函数值偏差预设为0.01，为避免搜索陷入局部最小值点，设置自适应函数值L1=L′+10，遗传算法具体的迭代过程如图9所示。

图9 遗传算法迭代过程Fig.9 Genetic algorithm iterative process

从图9遗传算法迭代过程可看出，在迭代8代以后的适应度函数值等于平均适应度函数值，评价函数值已无明显变化，即至少迭代8代即可求出最优解，即最优反馈控制率。

3 联合仿真分析

图12 铰接车路径跟踪仿真结果Fig.12 Articulated vehicle path tracking based circular path

利用ADAMS与Simulink的联合仿真来初步验证提出的控制策略的有效性。在Solidworks中建立包括铰接车、左右转向液压缸、前后车体、左右转向推杆等的铰接车三维模型，为了弥补实体模型导入后丢失的原有属性，在导入ADAMS模型后，定义各个零部件的质量，并为其添加约束。在ADAMS模型中，考虑铰接式车辆运行的巷道环境，采用二维随机不平路面，并参考E级路面修改路面谱系数，建立约束和驱动，基于ADAMS的铰接式车辆模型如图10所示。

图10 基于ADAMS的35 t铰接式车辆模型Fig.10 35 t articulated vehicle model based on ADAMS

搭建ADAMS和Simulink的联合仿真模型，本研究中的联合仿真路线如图11所示。

图11 联合仿真流程Fig.11 Block diagram of unity simulation scheme

根据图6所示的铰接式车辆路径跟踪控制策略进行联合仿真。在联合仿真中，对于铰接角的控制，根据地下巷道铰接车的安全行驶要求，车辆一侧与巷道壁间距最小为10 cm，且由于铰接车的结构限制，其前车体转角范围为[-45°，45°]，结合车身尺寸信息和规划理想路径信息，计算得maxεd=10 cm,maxεθ=12 rad,maxεc=0.038 4 m-1。

车辆跟踪的理想路径为圆心在全局坐标系原点，半径为25 m的圆形路径，车辆起点坐标为(35,10) m，车速选择3 m/s,仿真时长设为100 s，仿真结果如图12～16所示。图12a为铰接车跟踪理想路径效果图，在仿真时间100 s中，行驶路径与理想路径基本吻合且路径平滑，图12b为路径跟踪局部放大图，可看出，当预见路径的偏差为负，行驶路径偏差为正时，行驶的路径偏差有明显的减小趋势。反映了加入预见信息可补偿固有反应，加快反应速度。图13中车辆速度能在较短时间内达到并维持在3 m/s，表明速度控制有效；图14～16为路径跟踪偏差情况。

图14所示为铰接车路径跟踪控制中加入预见信息和未加入预见信息的跟踪位置偏差效果图，通过对比可看出基于预见信息的路径跟踪可以有效减小位置偏差的超调，提高反应速度，横向位置偏差最大偏差量不到0.2 m，最终偏差控制在0.03 m,相对于轮距2.3 m，误差仅为1.3%，对于最终稳态误差虽然仍处于工作允许范围内，但仍有提高空间。

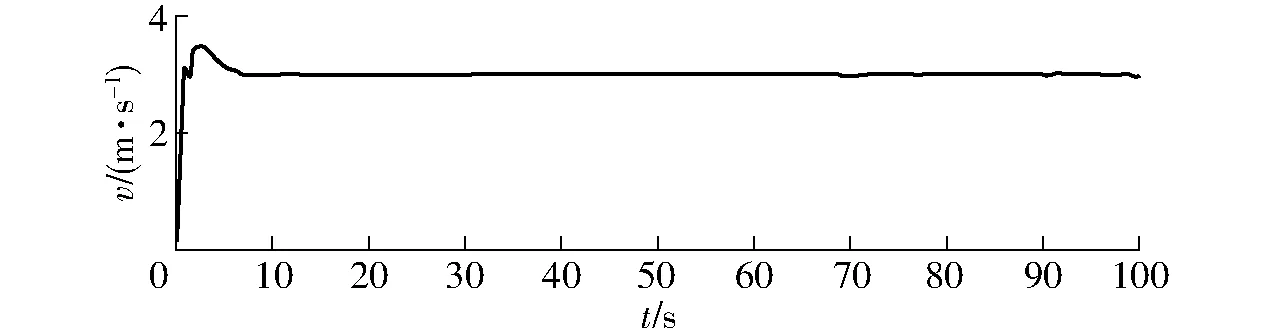
图13 车速控制结果Fig.13 Speed control results

图14 铰接车路径跟踪位置偏差Fig.14 Position error of articulated vehicle

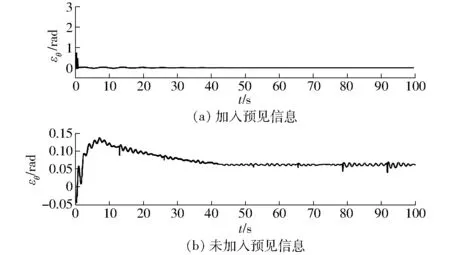
图15 行驶方向偏差Fig.15 Deviation of driving direction

图15所示为铰接车路径跟踪控制中加入预见信息和未加入预见信息的跟踪行驶方向偏差效果图，行驶方向偏差最终稳定在1.5×10-4rad，相比于铰接车转向角极值45°，误差为0.19%，通过对比可看出基于预见信息的路径跟踪对于行驶方向偏差的校正十分明显，加快了调节速度也减小了稳态误差，提高了车辆行驶的稳定性。

图17 USTB CYV-Ⅱ试验平台尺寸明细(单位：mm)Fig.17 Test platform dimension details of USTB CYV-Ⅱ

图16所示为铰接车路径跟踪控制中加入预见信息和未加入预见信息的跟踪曲率偏差效果图，通过对比可看出基于预见信息的路径跟踪减小了曲率偏差的最大超调，且同样快速将曲率偏差调节至0，波动范围小于0.003 m-1。仿真结果证明了提出的控制策略的有效性，试验中将进一步验证。

图16 曲率偏差Fig.16 Curvature deviation

4 试验

为进一步验证本文中铰接车路径跟踪控制策略的有效性，采用USTB CYV-Ⅱ作为试验平台进行试验分析，车体结构和尺寸明细如图17所示。USTB CYV-Ⅱ试验平台的车体结构与尺寸效仿铰接式车辆结构设计，运动学和动力学特性与铰接式车辆相符，可作为铰接式车辆路径跟踪控制策略的试验平台进行试验分析，试验场地选为楼道的部分区域，平面图如图18所示，跟踪路径选为有2个转弯的路径以充分验证控制系统性能。

USTB CYV-Ⅱ的行驶过程如图19所示，由于地面过于光滑且转弯半径较小，为保证车辆良好跟踪理想路径，车速选为1 m/s匀速行驶。

图18 试验区平面示意图Fig.18 Test area plane

图19 USTB CYV-Ⅱ的行驶过程Fig.19 Driving process of USTB CYV-Ⅱ

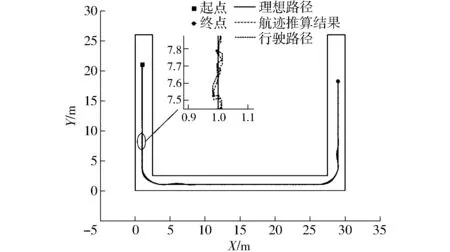
图20 USTB CYV-Ⅱ跟踪路径Fig.20 Path tracking of USTB CYV-Ⅱ

图21 跟踪速度与铰接角变化Fig.21 Change of tracking speed and articulation angle

图22 跟踪偏差Fig.22 Tracking error

跟踪结果及跟踪误差如图20所示，行驶路径与理想路径能够较好的贴合，且行驶路径较为平滑，车辆能够很好地沿着理想路径行驶，由局部放大图可知，预见位姿往往会呈现与理想路径间有更大的误差，从而使车辆能够得到一个更大的纠偏信号加快纠偏时间，使铰接车沿着理想路径行驶。图21为行驶速度和铰接角变化曲线，速度数据为控制器的输出数据，停车时由于车辆惯性导致了车辆滑行；铰接角变化平稳，两个弯道路段铰接角变化趋势相同，车辆具有较好的转弯特性。图22a为加入预见信息的位置偏差、行驶方向偏差和曲率偏差的变化情况，3个偏差均在直线行驶和曲线行驶时出现抖振，是由于车辆响应速度较慢以及楼道地面较为光滑，车辆出现侧滑导致，但仍符合铰接车的实际运行要求，在其他路段偏差均较小，其中，位置偏差基本维持在零值上下，波动约±0.03 m，与仿真结果一致，行驶方向偏差基本收敛于零值上下，波动约为±0.004 rad，曲率偏差基本在零值上下，最大值不超过0.003 m-1。试验中起始偏差量均较小是因为车辆在理想路径起点开始行驶，而仿真中车辆起点不在理想路径上。图22b为未加入预见信息的跟踪偏差结果，由图22a和图22b的对比可看出，加入预见信息减小了位置偏差和行驶方向偏差的超调，对于行驶方向偏差的改善效果十分明显，对于曲率偏差的调节作用较小，与仿真结果吻合，加入预见信息对于路径跟踪控制有一定的调节作用。试验结果表明了本研究中的铰接式车辆的路径跟踪控制策略的有效性，可用于铰接车的路径跟踪。

5 结束语

提出了一种基于预见信息的铰接式车辆LQR-GA路径跟踪控制方法，通过引入预见信息提高控制系统的反应速度，加入柔化以防止控制量过大。同时，提出了一种基于跟踪偏差的LQR-GA路径跟踪控制方法，GA算法对LQR中的状态量权重矩阵进行优化且达到了最优的控制效果。所提出的控制策略在仿真和试验中均取得了较好的控制效果，路径的跟踪位置偏差的误差为1.3%，行驶方位偏差误差为0.19%，曲率偏差基本维持在零值，极大地改善了铰接车路径跟踪精度，试验结果符合车辆巷道行驶要求，可用于铰接式车辆路径跟踪控制。

1 赵翾, 杨珏, 张文明,等. 农用轮式铰接车辆滑模轨迹跟踪控制算法[J/OL]. 农业工程学报, 2015, 31(10):198-203.http:∥www.tcsae.org/nygcxb/ch/reader/view_abstract.aspx?file_no=20151026&flag=1. DOI:10.11975/j.issn.1002-6819.2015.10.026.

ZHAO Xuan, YANG Jue, ZHANG Wenming, et al. Sliding mode control algorithm for path tracking of articulated dump truck[J/OL]. Transactions of the CSAE, 2015, 31(10):198-203.(in Chinese)

2 HEMAMI A, POLOTSKI V. Path tracking control problem formulation of an LHD loader[J]. The International Journal of Robotics Research, 1998, 17(2): 193-199.

3 PETROV P, BIGRAS P. A practical approach to feedback path control for an articulated mining vehicle[C]∥2001 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2001, 4: 2258-2263.

4 BIGRAS P, PETROV P, WONG T. A LMI approach to feedback path control for an articulated mining vehicle[C]∥7th International Conference on Modeling and Simulation of Electric Machines, Converters and Systems (Electrimacs), 2002:1-6.

5 RIDLEY P, CORKE P. Load haul dump vehicle kinematics and control[J]. Journal of Dynamic Systems, Measurement, and Control, 2003, 125(1): 54-59.

6 NAYL T, NIKOLAKOPOULOS G, GUSTFSSON T. Switching model predictive control for an articulated vehicle under varying slip angle[C]∥2012 20th Mediterranean Conference on Control & Automation (MED), 2012: 890-895.

7 邵俊恺, 赵翾, 杨珏,等. 无人驾驶铰接式车辆强化学习路径跟踪控制算法[J/OL]. 农业机械学报, 2017,48(3):376-382.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170348&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2017.03.048.

SHAO Junkai,ZHAO Xuan,YANG Jue,et al.Reinforcement learning algorithm for path following control of articulated vehicle[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2017,48(3):376-382.(in Chinese)

8 OGATA K, YANG Y. Modern control engineering[M]. 4th ed. Upper Saddle River, NJ:Prentice Hall, 2002: 826-910.

9 SHIROMA N, ISHIKAWA S. Nonlinear straight path tracking control for an articulated steering type vehicle[C]∥ICCAS-SICE, 2009: 2206-2211.

10 POLOTSKI V, HEMAMI A. Control of articulated vehicle for mining applications: modeling and laboratory experiments[C]∥Proceedings of the 1997 IEEE International Conference on Control Applications, 1997: 318-323.

11 DRAGT B J, CRAIG I K, CAMISANI-CALZOLARI F R. Navigation of autonomous underground mine vehicles[C]∥1st African. Control Conference, 2003: 3-5.

12 王亮, 卢永锦. 引用预见信息的人机耦合优化方法[J]. 北京航空航天大学学报, 2008, 34(4):361-364.

WANG Liang, LU Yongjin. Optimal method of human-machine coupling with preview information[J].Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(4):361-364.(in Chinese)

13 石峰, 战凯, 顾洪枢,等. 地下铲运机跟踪轨迹推算模型研究[J]. 有色金属：矿山部分, 2010, 62(6):66-69.

SHI Feng, ZHAN Kai, GU Hongshu, et al. A study on underground loader tracking track calculation model[J].Nonferrous Metals: Mining Section, 2010, 62(6):66-69.(in Chinese)

14 DA FONSECA NETO J V, ABREU I S, DA SILVA F N. Neural-Genetic synthesis for state-space controllers based on linear quadratic regulator design for eigenstructure assignment[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2010, 40(2): 266-285.

15 GARGOURI L, ZAAFOURI A, KOCHBATI A, et al. LQG/LTR control of a direct current motor[C]∥ IEEE International Conference on Systems, Man and Cybernetics, 2002.

16 KO H S, LEE K Y, KIM H C. An intelligent based LQR controller design to power system stabilization[J]. Electric Power Systems Research, 2004, 71(1): 1-9.

17 WANG L, NI H, ZHOU W, et al. MBPOA-based LQR controller and its application to the double-parallel inverted pendulum system[J]. Engineering Applications of Artificial Intelligence, 2014, 36: 262-268.

18 NIKNEZHADI A, ALLUÉFANTOVA M, KUNUSCH C, et al. Design and implementation of LQR/LQG strategies for oxygen stoichiometry control in PEM fuel cells based systems[J]. Journal of Power Sources, 2011, 196(9): 4277-4282.

19 HASANZADEH A, EDRINGTON C S, LIU Y, et al. An LQR based optimal tuning method for IMP-based VSI controller for electric vehicle traction drives[C]∥ Vehicle Power and Propulsion Conference (VPPC), 2011 IEEE, 2011: 1-7.

20 USTA M A, AKYAZI Ö, AKPINAR A S. Aircraft roll control system using LQR and fuzzy logic controller[C]∥ 2011 International Symposium on Innovations in Intelligent Systems and Applications (INISTA), IEEE, 2011: 223-227.

21 TSAI S J, HUO C L, YANG Y K, et al. Variable feedback gain control design based on particle swarm optimizer for automatic fighter tracking problems[J]. Applied Soft Computing, 2013, 13(1): 58-75.

22 OHRI J. GA tuned LQR and PID controller for aircraft pitch control[C]∥ 2014 IEEE 6th India International Conference on Power Electronics (IICPE), 2014: 1-6.

23 GHAZI R, KHAJEH A. GA-based optimal LQR controller to improve LVRT capability of DFIG wind turbines[J]. Iranian Journal of Electrical and Electronic Engineering, 2013, 9(3): 167-176.

24 WONGSATHAN C, SIRIMA C. Application of GA to design LQR controller for an inverted pendulum system[C]∥ IEEE International Conference on Robotics and Biomimetics, ROBIO 2008. IEEE, 2009: 951-954.