我国金融市场间的风险传染测度研究

纪伟伦

【摘要】随着经济的多元化、资本的大规模流动以及金融衍生品的不断发展，各个金融市场之间的关联程度越来越高金融风险传染度量成为了金融风险管理的一个重要内容。本文利用MSV模型，用收益率的波动来描绘风险，以相关系数的改变作为衡量金融风险传染发生的指标，选取了我国2014-2017年股票指数和债券指数的对数收益率进行了实证分析，并得到以下结论：我国股票市场和债券市场收益率均表现出尖峰厚尾的特征；股市债市之间存在着风险传染效应，且该效应在牛市时表现最为明显。

【关键词】金融风险传染测度，股票市场，债券市场，MSV模型

1 前言

金融风险的发生一直是金融市场发展过程中无法避免的一大难题。从上世纪末期开始，金融衍生品层出不穷，金融市场间关联程度越来越高。一旦某个经济体或金融市场爆发危机，其风险极易造成大范围经济动荡。以我国的股票市场和债券市场为例，如图1所示，2007-2016年股市与债市收益率波动走势近乎一致，表现出较强的相关性，这种现象在2008年和2015年表现尤为明显。

事实上，金融风险传染的相关研究一直都是金融界学者非常关注的课题。在金融风险测量方面，学者们渐渐摆脱了原有简单的测度模式。金融创新和信息科技的广泛应用使金融市场更新迭代速度有了大幅提升，传统的风险分析方法通常无法有效地度量市场间的溢出水平评估市场风险。因此在当今全球经济格局下寻找一个准确的金融风险传染度量方法就显得尤为重要。

2 文献综述

金融危机的频繁爆发使得金融市场间的风险传染成为金融风险研究领域的一个热点问题，诸多学者对风险传染进行了大量研究并取得诸多研究成果。

基于股市和债市在金融市场资产配置中的重要地位，学者们自金融发展早期开始便对两市场之间的关系进行了深入的研究。Keim等（1986）较早验证了股票市场和债券市场间存在的相关关系。Baur（2010）运用基于VAR的格兰杰因果检验方法，研究发达国家的股票和债券市场，发现了股市和债市之间存在双向格兰杰因果关系。Papavassilious（2014）运用DCC-GARCH模型针对希腊债务危机分阶段分别研究了不同市场走势下境内主要资本市场间的风险传染效应，其结果表明债务危机期间两个市场之间具有显著的风险传染效应。

相较于国外市场，中国股票市场和债券市场虽起步较晚尚未完全成熟，但随着政府相关政策的颁布实施，两个市场相关性得到大幅提升，受到了越来越多的关注。王璐等（2009）实证发现中国股市对债市的波动溢出效应较债市对股市的溢出效应更为显著。廖佳等（2014）从行为经济学角度着重研究了在不同金融环境下投资者对金融市场的情绪变化对跨市场金融传染效应的影响，实证发现市场情绪在不同市场行情下具有很强的独特性，其对市场间的相关性影响在不同市场行情下表现不同。

与文献相比，本文的创新性体现在：（1）模型的突破。本文将传统的SV模型扩展为多元并应用在股市和债市的风险传染性分析上。（2）数据的处理。本文将数据分为三个阶段进行对比，通过危机期与牛市期两个期间的前后对比，也为风险传染效应提供了实证。（3）计算方式的选择。本文选用了蒙特卡罗（MCMC）模拟进行模型的求解，大大提高了文中采用模型的实用性。

3 金融风险传染效应

3.1 金融传染效应的相关概念

首先，是关于风险的定义本文将采用广义的风险的定义，即不管是带来收益还是损失，皆可算作风险。Engle等学者（2002）将金融传染效应认定为受到风险冲击后不同金融市场间相关性显著增加的效应，该理论在度量金融传染效应的大小和传染方向等方面都得到了广泛的应用。本文将认定传染的发生是由相关性的改变来进行衡量的，同时为了简化分析，本文所讨论的金融风险传染效应排除共同冲击因素的基础性传染分析。只有这样，在建模时，市场与市场间才能看作两个独立变量，才能观测到一个市场的波动能否影响另一个市场。

3.2 金融传染效应研究方法

Taylor（1982）将随机波动原理应用到金融时间序列分析中，提出了随机波动（Stochastic Volatility， SV）模型。基本的一元SV模型如下

yt=μ+eht2εt

ht+1=α+βht+ηt

其中，εt～NO，1，ηt～N（0，ση2），二者相互独立。μ为时间序列均值，εt和ηt分别为均值方程和波动率方程的随机擾动项，β反映波动率序列的持续性。

多元SV模型在波动率方程基础上引入了一个服从马尔科夫过程或其他随机游走过程的新随机变量。构建模型的均值方程为

Yt=U+i=1kλiYt-i+Et （4.10）

其中，Yt=y1，t，y2，t，…，yk，tT，U=ui，u2，…，ukT，λi=λ1，i，λ2，i，…，λk，i，Et=eh11，t2ε1，t，eh22，t2ε2，t，…，ehkk，t2εk，tT，k代表的市场数，λ1，iyt-i表示的是均值溢出，包含了前期本市场和其它市场价格收益。Et是条件方差和扰动项的向量，hkk，t表示的是第t期市场k的风险或波动。进而可以得到两市场之间的随机风险传染方程

Ht+1=α+i=1kβiHt+ηt （4.11）

其中，Ht=h1，t，h2，t，…，hk，tT，α=α1，α2，…，αkT，βi=β1，i，β2，i，…，βk，i，ηt=η1，t，η2，t，…，ηk，tT，k代表的市场数，hii，t-1是单个市场收益已经实现的波动，hj j，t，hji，t-1分别为当期和前期风险传染项。通过观察均值方程中相关系数的改变，可以确定风险是否发生了传染；通过观察风险传染方程，可以量化确定风险传染的效应大小。

4 数据选取与实证分析

4.1 数据选取

本文选取2014-2017年上证综指、上证国债指数的对数收益来表示我国股市和债市的变动情况，分别表示为R1、R2，定义收益率表达式为Ri=lnt日指数收盘价t-1日指数收盘价，共1774个数据。所有市场指数数据均来自于国泰安CSMAR数据库。

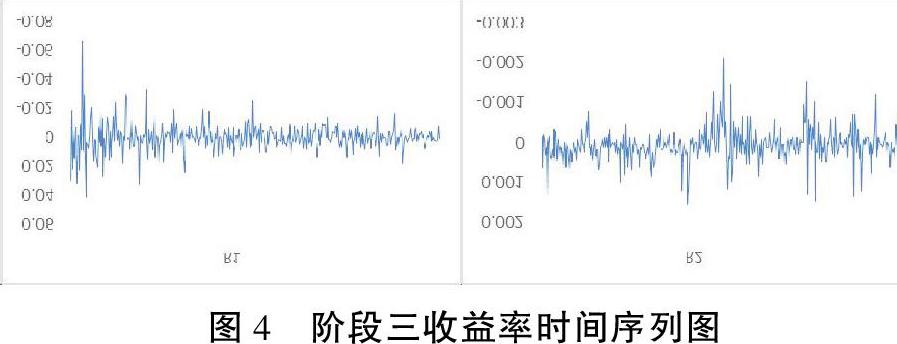
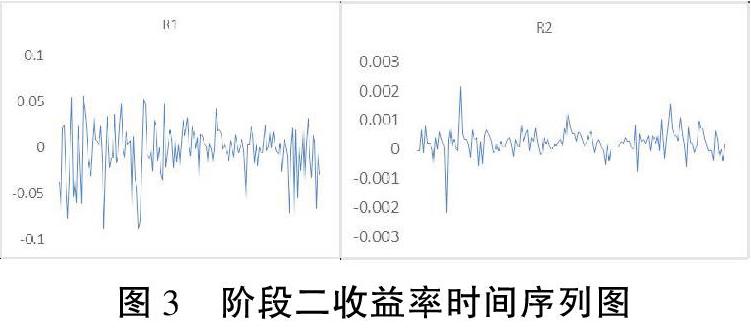
为了更好的分析风险传染效应，参考郑振龙等、袁晨等学者的行情阶段划分方法，将数据分为以下三个阶段：阶段一（牛市，2014年3月15日～2015年6月17日，共309个交易日）、阶段二（熊市，2015年6月18日～2016年1月28日，共152个交易日）、阶段三（震荡市，2016年1月29日～2017年10月30日，共426个交易日）。各阶段数据描述性统计分析如下：

由表1描述性统计分析可知，债市的波动远小于股市。J-B统计量在1%水平下显著，表明任意阶段两种指数收益率均不服从正态分布；同时由偏度和峰度值可知，收益率表现出显著的有偏的尖峰厚尾的特征。

由下图及图1来看，在每个阶段股市的波动均强于债市的波动性，即从单个市场的角度股市的风险相对来说高于债市；同时根据两个市场波动性出现的频率来看，两个市场之间表现出较高的相关性。

对于相关性，可以看出虽然波动幅度不同，但股债两市波动趋势相对一致。此外，收益率时间序列图还反映了序列的波动集聚性特征，即在一个大波动后面往往跟着另一个大波动，同样一个小波动后面亦跟随着另一个小波动。

4.2 单位根检验

SV类模型均隐含了一个假设，即要求所选时间序列必须为平稳序列，因此在利用时间序列建模时首先应先对其平稳性进行检验，以使模型结果更为精确。利用Eviews软件对上述8列收益率序列进行单位根检验，其结果如下表2所示。

由ADF检验值和P一值可知，在三个不同阶段，两种收益率序列均在1%显著水平下拒绝原假设，即收益率序列均是严格平稳的。同时，根据ADF检验输出结果可知，在建模时最佳滞后阶数为1。

4.3 格兰杰因果检验

为研究股市和债市的收益率之间是否存在这必然的因果关系，本文将对股票市场和债券市场收益率序列基于VAR模型进行格兰杰因果检验，其中VAR模型基本设定如下所示

R1，t=c1+α1R1，t-1+β1R2，t-1+ε1，t （5.1）

R2，t=c2+α2R1，t-1+β2R2，t-1+ε2，t （5.2）

由参数估计结果可知，在不同市场行情下股票市场历史行情对股债两市市场行情均有显著影响，且除去阶段二（熊市）阶段对债市的影响外，其余时段均表现为正相关关系。而债市方面，则表现不同。在牛市、熊市及总体阶段上，债券市场的历史行情对股票市场的影响均表现为统计意义上的不显著。就整个估计区间行情来看，股债两市间的影响方向与阶段一（牛市）行情影响相同。

在VAR模型回歸结果基础上，运用格兰杰因果关系检验对收益率序列的因果关系进行分析研究。利用软件进行分析结果如下表4所示。由格兰杰因果检验结果可知，在阶段一（牛市），F统计量和P-值结果均表明在1%显著性水平下均拒绝原假设，即表明股票市场和债券市场间均存在着双向收益率传导关系。另外，在阶段二（熊市），F统计量和P-值结果均表明在10%显著性水平下，R2是R1的格兰杰原因，即债券市场对股票市场存在弱传导效应。震荡市阶段及总体估计区间内，股票市场和债券市场均不存在传导效应。

4.4 MSV模型

本文主要将在MSV模型的波动率方程中引入马尔科夫链模拟未来行情波动，采用吉布斯（Gibbs）抽样方法进行蒙特卡罗（MCMC）方法模拟从而实现模型的动态模拟。根据金融市场的实际情况以及SV模型的约束对模型做出如下假设：

假设1：相同市场的均值方程扰动项与波动方程的扰动项不相关，不同市场间的均值方程扰动项不相关，不同市场间的波动方程扰动项不相关。

假设2：风险传染方程的扰动项与均值方程的扰动项不相关，风险传染方程的扰动项与波动方程的扰动项不相关。

鉴于股市和债市的二元结构，建立两市场滞后一阶的MSV模型均值方程如下所示

Y1，t=u1+λ11Y1，t-1+λ1Y2，t-1+eh11，t2ε1，t （5.4）

Y2，t=u2+λ12Y1，t-1+λ22Y2，t-1+eh22，t2ε2，t （5.5）

波动率方程如下所示

h11，t=，011+bllh11，t-l+b21h21，t-1+Q112，q11，t （5.6）

h22，t=，622+b22h22，t-l+b12h12，t-1+Q222rI22，t （5.7）

风险传染方程如下所示

h12，t=υ12+c12h12，t-1+d11h11，t-1+d22h22，t-1+σ122η12，t

（5 .8）

h21，t=，621+c21h21，t-1+c11h11，t-1+c22h22，t-1+σ2127η21，t

（5.9）

进行MCMC模拟估计，将先验分布设置为σij2～Inverse Gam-ma（2.5，0.025）分布，bij*、cij*、cii*、dii*～Beta（20，1.5），其中，bij*=（bij+1）2，cij*=（cij+1）2，cii*=（cii+1）2，dii*=（dii+1）2，ui，λij、αij～N（0，0.0001）。所有先验分布均相互独立。

由于模型着重对相关系数的分析，本文只列出了风险传染方程中入LL（前期股票市场收益的影响系数，λ21（前期债券市场收益的影响系数）、b11b22（波动方程中前期本市场收益波动系数）、b12b21（波动方程中其他市场收益波动系数）、c12c21（风险传染方程中的前期风险传染项系数）、c11c22d11d22（风险传染方程本市场已实现收益的波动系数）进行研究分析。

从表5中各个参数的估计结果可以看出，阶段三震荡市期间及总体样本区间两市场间收益均值溢出效应不明显，故省略讨论。同一时间段牛市前后股债两市之间存在显著的均值溢出，即λ12、λ21估计值不为0。同时根据跨阶段系数符号变化，危机的冲击使债市对股市收益的影响由正变负，股市对债市收益的影响由负变正。而这也符合现实中经济规律，牛市的到来使股票市场行情变好，理性投资者为追求利益会增大股票持有量，减少债券投资；危机发生时，股票市场行情下挫，投资者相应地会将资金由股市转移到债市。其次，从波动方程系数看，阶段一牛市时股市的收益波动（即风险）与前期债券市场的风险传染（b21）成正比，而阶段二熊市时两者则成反比关系；这意味着牛市结束后，债券市场的波动会使股市波动减弱。对于债券市场来说，危机的产生使其市场收益波动与本市场前期的收益波动的相关性（b22）由负变正。最后，由风险传染方程的系数来看，危机的出现改变最明显的是风险传染项与已实现收益波动之间的关系。危机发生前，股票市场和债券市场间风险传染项均与前期股市的收益波动（c11、d11）呈正相关，与债市收益波动（c22、d22）呈负相关；危机发生后，则呈现相反的关系。这也就是说，危机的产生影响了风险传染项的系数，改变了市场间波动对风险传染项影响的方向和大小。

同时从上表来看，危机的产生对债券市场和股票市場的相关性影响较为明显。牛市后两个市场的均值溢出效应产生了改变，说明风险在两个市场间发生了传染。波动方程和风险传染方程则进一步解释了造成风险波动和市场间风险传染的因素，从另一方面验证了风险传染的发生。

5 结论与建议

本文选取2014年3月—2017年10月上证综指和上证国债指数的对数收益对股市和债市间的风险传染测度进行研究。通过对样本数据描述性统计分析和模型分析，最终得到结论如下（1）股票市场和债券市场收益率序列均表现出波动聚集性、尖峰厚尾的特征；（2）股债两市之间的风险传染效应在牛市行情下表现最为明显；具体而言，在牛市行情下股票市场对债券市场的传染效应要强于债券市场对股票市场的传染效应。

基于本文的研究，对我国的风险管理部门提出的政策建议如下：首先，资本市场是一个整体，建立一个资金多层次自由流动、大容量的金融市场的需求愈发迫切。其次，不管是在制定实施相关市场管理政策，还是在建立完善风险预警管理机制方面，监管部门都应充分考虑不同市场间风险传染的存在。最后，我国应该加强资本市场改革，建立完善的信息传导机制，有效降低信息成本，从而降低金融市场的大起大落的可能，维护市场秩序，从而达到保障投资者权益的目的。

参考文献：

[1]Keim，D. B.，Stambaugh R. F.，Predicting Returns in the Stock andBondMarkets[J].Journal of Financial Economics，1986，17（2）：357-390

[2]Baur D.G.，Stock-Bond Co-Movements and Cross-CountryLinkages[J].International Journal of Banking，Accounting and Finance，2010，2（2）：111-129

[3]Papavassiliou V.G.，Cross-Asset Contagion in Times ofStress[J].Jour-nal of Economics and Business，2014（76）：133-139

[4]王璐，庞瞧.中国股市和债市波动溢出效应的MV-GARCH分析[J].数理统计与管理，2009，28（1）：152-158

[5]许祥云，廖佳，吴松洋.金融危机前后的中国股债关系分析——基于市场情绪变化的解释视角[J].经济评论，2014（1）：130-140

[6]郑振龙，杨伟.金融资产收益动态相关性：基于DCC多元变量GARCH模型的实证研究[J].当代财经，2012，（07）：41-49

[7]袁晨，傅强.我国金融市场间投资转移和市场传染的阶段时变特征——股票与债券、黄金间关联性的实证分析[J].系统工程，2010，28（5）：1-7