具有B-D非线性传染率的SIQ传染病模型*
2018-07-06马晓丽冯孝周王国珲
马晓丽,徐 敏,冯孝周,王国珲
(1.西安工业大学 理学院,西安 710021;2.陕西航天机电环境工程设计院有限公司,西安 710100 3.西安工业大学 光电工程学院,西安710021)
目前,世界上已经有近半数人的健康受到各种传染病威胁.例如,2009年,甲型H1N1流感波及世界各国,并给各国的财力、物力以及国民的生命造成巨大损失.甲型H1N1其实是一种急性呼吸道疾病,在人群中通过空气传播.甲型H1N1流感的病原体是一种新型病毒,在人群密度高的种群中容易传播,其患病症状主要表现为身体发热、喉咙疼痛、咳嗽不止、身体疼痛和发冷以及头痛疲劳等,根据世界卫生组织对其研究和数据统计显示:截至2009年底,已经有至少12220人因为甲型H1N1传染病而死亡.总之,它已经对世界各国人民的生命健康造成严重的危害,同时给世界各国的经济发展也带来了很大程度上的损失.
对于早期诸如H1N1、SARS等传染病控制策略均是非常有效的预防种群传染病感染及扩散的数学工具[1-6].本文将研究具有非线性项的SIQ(Susceptible Infectious Quarantine)传染病模型解的全局性质.传染病的传播动力学的发生率和传染病模型各种相关比率规律已被广大学者所关注,并且取得较多研究成果[7-8].一般地种群模型,假设种群可以分别记为S=S(t)是易感种群,I(t)为被感染种群,Q(t)为被隔离的种群,R(t)为康复种群,发病几率是经典的情形.设S和I为双线性的[9-10],比如βSI.但是当模型具有形如H(S,I)非线性发病率时,传染病模型就出现许多丰富的动力学结构[11-16].在文献[11-13]中只考虑了非线性发病率Holling反应项的模型稳定性,而文献[14-16]分别研究了非线性发病率H=βSI2/(1+mI2)与H=KSI/(1+αI2)的模型稳定性,以上这些模型均未考虑易感种群与感染种群之间的内部影响.因此,文中主要关注具有非线性发生率SIQ流行病隔离模型H(S,I)=βS/(1+mS+KI).
假设研究的种群具有一个非常短的免疫周期是可以忽略的,并且不考虑康复因素,只研究SIQ的传染病模型,具体模型如下:
(1)
其中A表示种群的一个恒定迁移率,d为各种群的自然死亡率,α1和α2分别为被感染种群I(t)与被隔离种群Q(t)的死亡率,δ为从被感染种群I(t)到隔离种群Q(t)的转移率,r,ε分别表示被感染种群与隔离种群的免疫力失去率,并且假设常数d,δ,A为正数,r,ε,α1和α2为非负常数.
对系统(1),整理变形,可得N满足:
N′(t)=A-dN-α1I-α2Q≤A-dN,

(2)
根据上面估计式可知,系统(1)初值解满足:
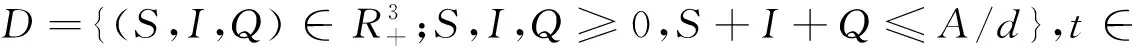
且在D上为不变子集.
1 平衡解的局部稳定性
为了研究系统平衡解的稳定性,下面求解系统(1)的平衡点,具体如下:
且可以得到两个解,P0(A/D,0,0))和P1(S1,I1,Q1)∈R3,其中P1(S1,I1,Q1)满足:
由(ii)可得:
且β>Km(r+d+δ+α1);
由(i)可得:
下面定义如下阈值
则P1∈D,当且仅当R<1.
接下来利用线性化方法研究系统平衡解的局部稳定性.
定理1 如果R>1,系统(1)的无感染平衡解P0是局部渐进稳定的,如果R<1,则系统(1)的感染平衡解P1是局部渐近稳定的,而P0变得不稳定.
证明:首先考察系统(1)在无感染平衡点P0处的稳定性,在P0点处雅可比矩阵如下:
而J(P0)的特征值为

接下来研究感染的平衡点P1的稳定性,对系统(1)在点P1处线性化如下:
从而通过化值整理可知:
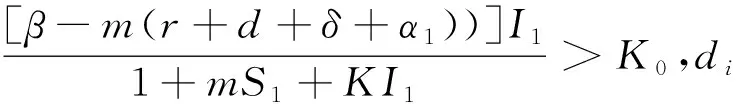
故简化的J(P1)为如下形式:
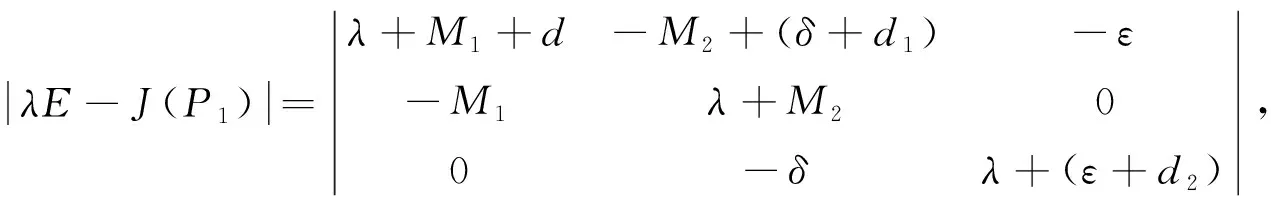
整理化简可得如下特征方程:
λ3+a1λ2+a2λ+a3=0,
其中,a1=M1+M2+d+d2+ε>K0;
显然a1a2-a3=(M1+M2+d)a2+(d2+ε)2(M1+M2+d)+εM1δ>K0
根据Hurwitz条件可判定:系统(1)在P2点处是局部渐近稳定的.
2 平衡解的全局稳定
本节主要研究平衡解P0和P1的全局稳定性,对于系统(1),非线性发生率f(S,I)=βS/(1+mS+KI)在[0,+)关于S是单调递增的且δ+r+d+α1∈[0,+),S,I,Q∈[0,A/d],把这些事实用符号H标记,以便下文论述.显然而则η0≅
定理2 对于系统(1),如果R>1,则系统的无感染平衡点P0是全局渐近稳定的;如果R>1,则P0是不稳定的,而系统(1)在感染的平衡点P1处是全局渐近稳定的.
证明:研究无感染的平衡点P0的稳定性,由系统(1)中的第二个方程可知:∀A0>KA/d,存在t0>K0使得S(t),Ι(t)≤Ν(t)≤A0.对于t≥t0,令C≅f(A0,0)-(r+d+δ+α1).如果R>K1,则选A0,使得C1<0,由f(S,I)性质可知f(S,I)≤f(A0,0),t≥t0,且I′(t)≤(f(A0,0)-(r+d+δ+α1))I(t)=C1I(t),t≥t0,从而解得:I(t)≤I(t0)eC1(t-t0)→0,当t→.
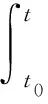
利用I(t),Q(t)的估计可知,当t→时,Q(t)→0,则S(t)=S(t0)e-d(t-t0)-e-d(t-t0)[A-f(S(τ),I(τ))I(τ)+rI(τ)+εQ(τ)edτ]dτ→A/d.
因而,系统在P0点处全局渐近稳定,而当R<1,则在P0点处线性化系统有一个正特征值,故P0不稳定.
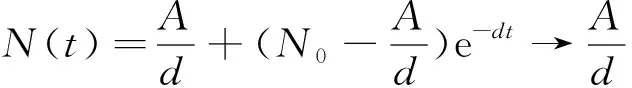
当t→,利用文献[13]中判断稳定性方法知:
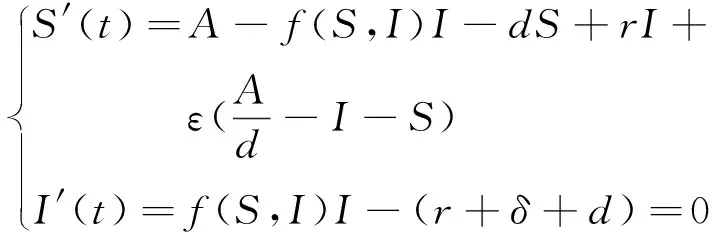
(3)
因为
从而,我们可以把系统(3)写成下面形式,
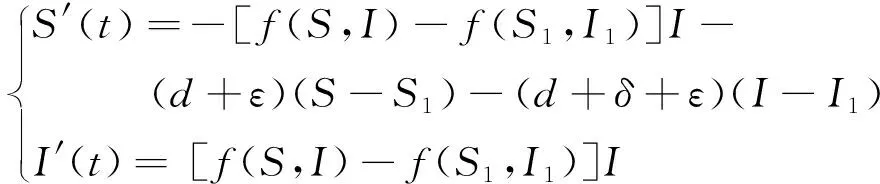
(4)
当R<1时,(S1,I1)在区域D+={(S,I);S≤0,I>0},为了证明对系统(4)而言,(S1,I1)是全局稳定的,我们利用Lyapunov正交化方法,选取如下形式的Lyapunov函数:
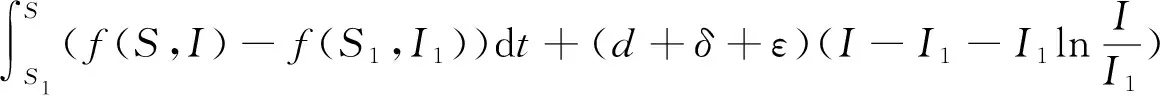

=-(f(S,I)-f(S1,I1))2I+(d+ε)(f(S,I)-f(S1,I1))(S-S1)≤0
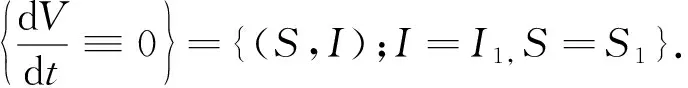
因此,(S1,I1)是全局渐近稳定的.
当α1,α2≠0时,为了论证系统(1)在点P1处的全局稳定性,引入变换
N=S+I+Q,则系统(1)可转化为:
(5)
则系统(5)对应的平衡态点为(N1,I1,Q1),且满足N1=I1+Q1+S1为进一步简化系统,令:x=N-N1;y=I-I1;z=Q-Q1,则系统(5)可化为:
(6)
令Λ≅-β-m(r+d+δ+α1),则由系统的比较原理可知式(6)的上限系统为
则只需要讨论如下系统的稳定性.
(7)
接下来选择如下的Lyapunov函数:
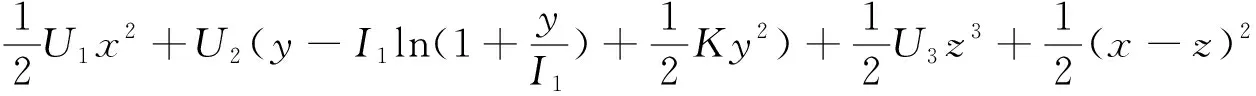
关于t求导可得:

=-d(1+U1)x2+(ΛU2-α1U1-(δ+α1))xy+(-U1α2+2d+ε)xz-U2(K+Λ)y2+(-U2Λ+U3δ+(δ+α1))yz-[U3(ε+d+α2)+(ε+d)]z2.
选择如下的U1,U2,U3>K0:
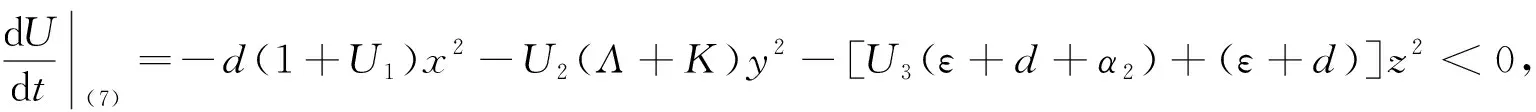
因此,系统(1)的感染的平衡点(S1,I1,Q1)是全局渐近稳定的.
3 数值模拟
本节根据现实中的某种传染病在人群中的传染,给出近似于符合实际情况的参数设置,利用Matlab对模型(1)进行数值模拟.具体对系统(1)
中各个参数按照我们定理1与定理2中的假设条件取值,从而验证我们得到的理论结果是否正确.
1) 当R0=0.026<1,且A=0.003,β=0.015,m=0.065,K=0.093,d=0.006,r=0.001 5,ε=0.000 9,δ=0.004,α1=0.008,α2=0.007,S0=0.98,I0=0.02,Q0=0.1.
模型中的方程之间的变化关系及不同种群数量随时间t的变化趋势如图1(a)、图2(a)、图3(a)、图4(a)所示.
(2) 当R0=2.62>1,且A=0.1,β=0.015,m=0.007,K=0.093,d=0.006,r=0.001 5,ε=0.000 9,δ=0.004,α1=0.008,α2=0.007,S0=0.98,I0=0.02,Q0=0.1.
模型中的方程之间的变化关系及不同群体数量随时间t的变化趋势如图1(b)、图2(b)、图3(b)、图4(b)所示.
通过对上面Matlab数值模拟图形的对比,可以验证定理1、定理2的结论是正确的,即:当阈值R0<1时,系统(1)只有一个无感染的平衡点P0是全局渐近稳定的;而当R0>K1时,系统(1)存在一个全局渐近稳定的感染平衡解P1.
而通过上面几幅图之间的对比,很显然,可以得到当阈值R0大于或小于1时,S~Q,I~Q,S~Q之间的数量依赖变化关系,具体结果如下:
1) 图2(a)说明当R0<1时,感染人群I随着移出人群Q的数量增加而增加,而图2(b)说明当R0>K1时,感染人群I随着移出人群Q的数量增加而增加,但会达到一个峰值之后趋于稳定.
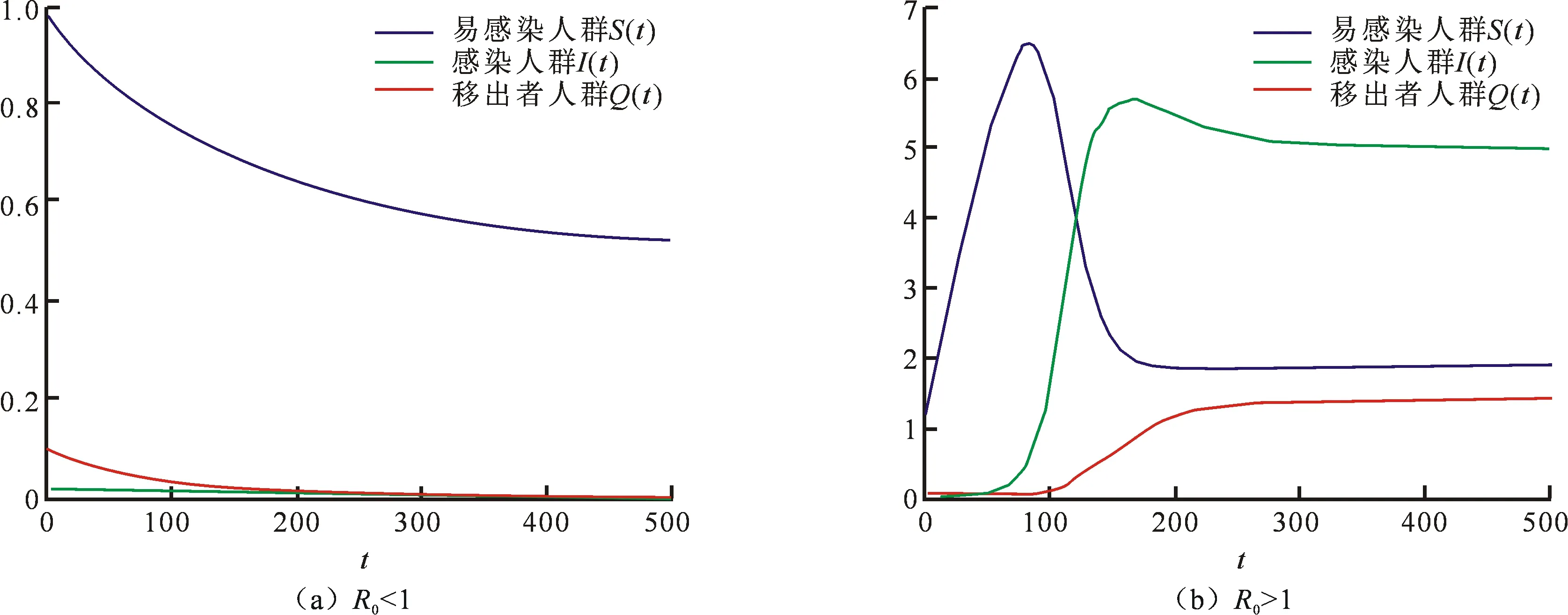
图1 SIQ模型的解Fig.1 The solutions of the SIQ model
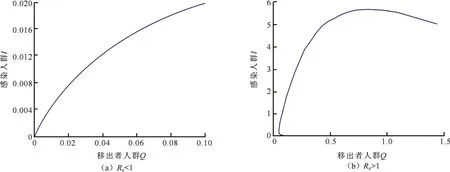
图2 I-Q依赖关系Fig.2 The dependence of I on Q
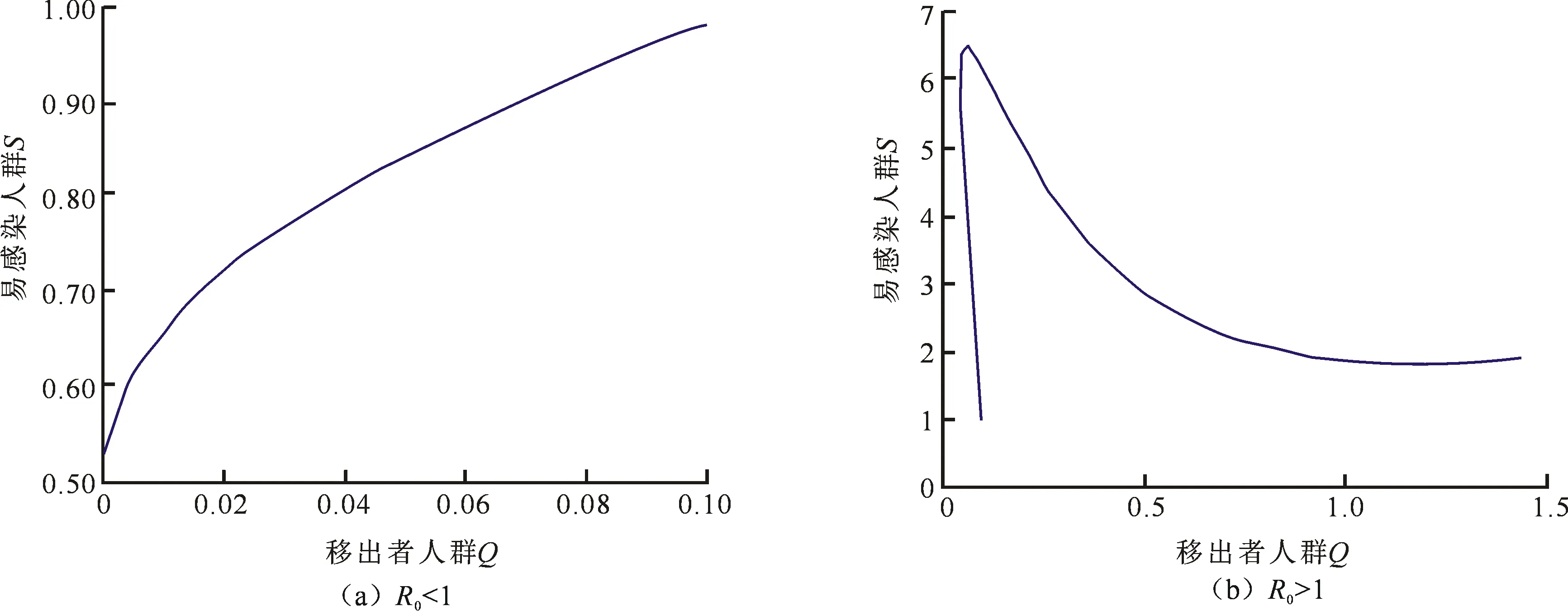
图3 S-Q依赖关系Fig.3 The dependence of S on Q
2) 图3(a)说明当R0<1时,易感染人群S随着移出人群Q的数量增加而增加,而图形图3(b)说明当R0>K1时,易感染人群S随着移出人群Q的数量增加而增加,但会达到一个峰值之后递减.
3) 图4(a)说明当R0<1时,易感染人群S随着感染人群I的数量增加而增加,而图4(b)说明当R0>K1时,易感染人群S随着感染人群I的数量增加而增加,但会达到一个峰值之后递减.
4 结 论
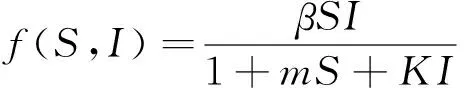
参考文献:
[1] ZEUZEM S,SCHMIDIT J M,LEE J H,et al.Dynamics of Hepatitis B Virus Infection in Vivo[J].Hepatology,1997,27(3):431.
[2] NOWAK M J,DE M R,HONKOOP P,et al.Viral Dynamics in Hepatitis B Virus Infection[J].Proceedings of the National Academy of Science of USA,1996,93(9):4398.
[3] NOWAK M A,MAY R M.Viral Dynamics[M].Oxford:Oxford University Press,2000.
[4] LENTEREN J C V,WOETS J.Biological and Integrated Pest Control in Reenhouses[J].Annual Review of Entomology,1988,33:239.
[5] ARCLAY H J.Models for Pest Control Using Predator Release,Habitat Management and Pesticide Release in Combination[J ].Journal of Applied Ecology,1982,19:337.
[6] XIAO Y,Bosch F V D.Dynamics of an Eco-epidemic Model with Biological Control[J].Ecological Modelling,2003,168:203.
[7] TANG S Y,CHEN L S.Periodic Predator-Prey Lotka-Volterra Model with Impulsive Effect[J].Journal of Mechanics in Medicine & Biology,2002,2(4):267.
[8] TANG S Y,XIAO Y N,CHEN L S,et al.Integrated Pest Management Models and Their Dynamical Behaviour[J].Bulletin of Mathematical Biology,2005,67:115.
[9] TANG S Y,XIAO Y N,CHEKE R A.Multiple Attractors of Host-parasitoid Models with Integrated Pest Management Strategies:Eradication,Persistence and Outbreak[J].Theoretical Population Biology,2008,73:181.
[10] XIANG Z Y,SONG X Y.The Dynamical Behaviors of a Food Chain Model with Impulsive Effect and Ivlev Functional Response[J].Chaos Solitons & Fractals,2009; 39 (5):2282.
[11] TANG S Y,TANG G Y,CHEKE R A.Optimum Timing for Integrated Pest Management:Modeling Rates of Pesticide Application and Natural Enemy Releases[J].Journal of Theoretical Biology,2010,264:623.
[12] LI C T,TANG S Y.The Effects of Timing of Pulse Spraying and Releasing Periods on Dynamics of Generalized Predator-prey Model[J].International Journal of Biomathematics,2012,5(1):1.
[13] 胡新利,金上海.具有阶段结构的捕食-食饵模型的稳定性及Hopf分支[J].纺织高校基础科学学报,2015,28(2):193.
HU Jinli,JIN Shanghai.Stability and Hopf Bifurcation of a Predator-prey Model with Stage Structure[J].Basic Sciences Journal of Textile Universities,2015,28(2):193.(in Chinese)
[14] 王丽丽,徐瑞.一类具有治愈率的HBV病毒感染模型的全局稳定性[J].生物数学学报,2014,29(2):253.
WANG Lili,XURui.Global Stability of an HBV Infection Model with Cure Rate[J].Journal of Biomathematics,2014,29(2):253.(in Chinese)
[15] 陈晓,闵乐泉,孙起麟.改进的HBV感染模型动力学分析及数值模拟[J].生物数学学报,2013,28(2):278.
CHEN Xiao,MIN Lequan,SUN Qilin.Dynamics Analysis and Numerical Simulation of An Amended HBV Infection Model[J].Journal of Biomathematics,2013,28(2):278.(in Chinese)
[16] 周艳丽,张卫国,原三领.一类随机SIRS传染病模型的持久性和灭绝性[J].生物数学学报,2015,30(1):79.
ZHOU Yanli,ZHANG Weiguo,YUAN Sanling.Persistence and Extinction in Stochastic SIRS Epidemic Model[J].Journal of Biomathematics,2015,30(1):79.(in Chinese)
