烟草商业系统物流线路优化研究与应用

章惠民

福建省烟草公司漳州市公司，信息中心，福建省漳州市芗城区元光北路19号金叶大厦 363000

烟草物流配送是现代化物流系统中的一个重要环节。现代商业系统卷烟物流强调快速响应，需要不断提高对环境变化和内部变化做出相应调整的适应能力。在经济新常态以及烟草行业降本增效的大环境下，着力推进精益物流以及智慧物流建设，提升配送效率、降低物流成本、提高服务水平，是烟草行业制胜的法宝。

按照传统模式，漳州烟草物流在卷烟配送过程中，为通过提高车辆利用率降低物流成本，调度人员常将地理位置集中的零售户统一配送。一般都只是根据行政区域划分固定送货线路，每条送货线路对应固定送货车辆和人员。不论是销售旺季还是淡季，物流每天所使用的车辆和人员数量都没有做相应的增减。尽管借助软件系统对送货线路进行优化，但也只是在原有基础上进行静态调整，无法根据每天的实际情况进行送货线路的动态实时优化，在节省人力、精简车辆、降低油耗等方面效果都不明显。

1 综述

1.1 国内外研究现状

重庆烟草物流配送区域划分为若干个配送单元，并依据配送单元的需求量、配送成本、配送中心及中转站的固定成本和变动成本, 建立了物流配送区域划分规划的运筹学模型, 应用遗传算法设计了编码方式和选择、交叉、变异算子配送区域划分的优化布局方案[1]。

湖南烟草工业公司以及湖南烟草商业系统为优化湖南烟草工商物流和商业系统卷烟配送物流操作流程，运用 GPS、GIS 、GPRS 等技术，采用基于启发式的禁忌搜索聚类算法、车载导航系统等，建立了一套完整的智能化卷烟物流在途动态监管系统，大幅提高卷烟商业配送运输效率，降低配送成本[2]。

日本烟草公司专门设置了物流部来负责卷烟配送服务，物流部的卷烟配送业务全部由其卷烟配送服务网络公司TSN（Tobacco Service Net）完成。TSN成功建设了国内外卷烟共同流通渠道，采用基于最短路径的网络优化算法，每辆车的配送线路、装载量、配送时间都由配送系统自动做出安排。

1.2 漳州烟草配送区域及线路优化概述

目前漳州烟草配送区域及线路优化借助柔性线路截取算法以及GIS线路优化辅助系统，依据零售户的地理位置、历史销量对全区所有零售客户进行线路调整，改变传统既定计划、线路、车辆、人员 “以线定车”的固定配送模式，建立了“以量定车，以户定线，户量均衡，动态优化”的弹性送货新模式。

弹性送货新模式打破了以往行政区划以及配送区域的概念，支持随访随销，较大程度地提高了配送方案调整能力、配送计划变更能力、协同配送能力和配送策略灵活性，力求以最优的线路、最短的时间，最少的精力、最低的成本完成物流作业，从而达到半径最佳、流向最畅、流速最快、流量最优的目标。

2 配送线路优化算法

卷烟物流配送优化是个非常重要的问题[2]。配送线路优化的结果，不仅会影响送货的效率和成本，也会影响其它与之相关的业务和作业，最终影响卷烟物流企业的经营。

2.1 线路优化问题描述

卷烟配送经验线路截取优化问题可以描述为：已知配送区域内的零售客户以及其在经验线路中的排列次序，给定该区域可用车辆及其标准配送能力，根据零售户订单情况，将经验线路截取并分配到各可用车辆中，使配送调度最优化。

考虑到频繁的零售户变更和送货次序对配送人员的工作效率影响较大，以往常用的调度策略是：预先划分出统一配送的区域，并为该配送区域内的零售客户分配车辆，同一配送区域内所有的零售户被编排到一条大线路（称之为经验线路）中。当零售户订货量随时间发生变化时，根据配送区域经验线路中指定的配送次序和车辆的配送能力，将当日零售户订单依次截取并分配给各配送车辆，生成所有车辆执行的配送小线路（称之为实时线路）。

配送调度最优化表现为以下方面：（1）车辆利用率最大化；（2）配送里程最小化；（3）工作量均衡化。其中，车辆利用率最大化和配送里程最小化，通过节省车辆和节省配送里程 保证了配送成本最小化；工作量均衡化，则通过减小工作任务的差异性，保证了 管理成本的最小化。通过配送成本最小化和管理成本最小化的统一平衡，实现配 送调度的最优化。

在问题求解中，配送里程为参与配送的各部车辆自物流中心出发，沿着实时线路访问各客户点，并在配送完成后返回物流中心所产生的行驶里程的总和。任意两点之间（物流中心到客户点、客户点到客户点，或客户点到物流中心）的行驶里程为基于两点坐标和实际电子地图路网数据计算出的最短路径长度。配送车辆的配送能力表现为配送户数和配送货量两个方面。在订货量波动较大的特殊时期(如春节、中秋等高峰期），调度人员可根据经验适当调整车辆配送能力浮动参数，使优化结果最大程度满足实际应用需要。

2.2 线路优化问题分析

全局配送线路优化核心问题是选取候选车辆以及依据候选车辆参数截取实时线路。

2.2.1 最佳候选车辆选取

车辆的配送能力描述为载货量和服务客户数量两个方面。对于候选车辆i，预先设定其标准装载量为SWi，标准配送客户数为SCi，假设其实际送货量为RWi，实际送货户数为RCi。此时，车辆i的工作负荷指标有：货量满载率户数满载率车辆i的任务满载率定义为TRi=min（CRi，CWi）。

设候选车辆列表中有k辆车，假设车辆i（i=1，2，…，k）标准装载量为SWi，标准配送客户数为SCi。依据车辆i的标准装载量和标准客户数，得到的实时线路中实际送货量为RWi，实际送货户数为RCi，则K辆车任务满载率最高的车辆j被选为最佳候选车辆，即满足TRi=max(TRi)，i=1，2，…,k。

2.2.2 实时线路硬性截取法

经验线路上的n（n ≥1）户零售户以自然数1…n编号。对于候选车辆i，预先设定其标准装载量为SWi，标准配送客户数为SCi。对车辆i分配的实时线路为经验线路中截取的前t户零售户（1≤ t ≤ n），t应满足：,且t ≤ RCi。为保证车辆利用率最高，t还应满足：SCi＜t+1。对于候选车辆i，假设经验线路中截取的前s（1≤ s ≤ n）户零售户可以满足t≤ SCi＜ t+1，则将经验线路中的前d户零售户截取为车辆i的实时线路，其中d=min(s，t)。由于按照此方式，对车辆i的实时线路截取严格依据标准装载量SWi和标准配送客户数SCi，该方法被称为硬性截取法。

2.2.3 实时线路柔性截取法

为适应节假日和销售淡旺季零售户订货量显著浮动的需要，并在配送成本最 小化的基础上实现工作负荷均衡化，在定义车辆i的标准装载量SWi和标准配送客户数SCi的同时，定义以下浮动参数：

L_SWi表示标准装载量下界，有 0＜L_SWi ≤SWi；

U_SWi表示标准装载量上界，有SWi≤ U_SWi；

L_SCi表示标准配送客户数下界，有0＜L_SCi ≤SCi；

U_SCi表示标准配送客户数上界，有SCi ≤ ＜U_SCi。

称[L_SWi，U_SWi]为标准装载量窗口，[L_SCi，U_SCi]为标准客户数窗口，并将依据标准装载量窗口和标准客户数窗口截取实时线路的方法称为柔性截取法。

柔性截取法的求解思路：首先，依据标准装载量下界L_SWi和标准配送客户数下界L_SCi进行实时线路的硬性截取，得到截取线路零售户的最小值dL；然后，依据标准装载量上界U_SWi和标准配送客户数上界U_SCi进行实时线路的硬性截取，得到截取线路零售户的最大值dU；最后，针对前两步得到的零售户截取窗口[dL , dU]，计算得出最优线路截取零售户d值d。

截取线路零售户最小值和最大值的计算方法参考实时线路硬性截取算法。对于零售户截取窗口[dL, dU]，有 1≤ dL ≤ dU ≤ n]。

图1 零售户截取窗口及截取前后路程变化示意图Fig.1 Sketch map of retail customer's interception window and interception distance

图1截取窗口[dL , dU]中零售户，当截取经验线路中前d户的零售户作为实时线路时，原来经验线路中连接零售户d和d+1 的边将被去除；实时线路中配送完零售户d后，车辆将返回物流中心，去除实时线路后的经验线路。

2.3 改进的柔性优化算法

基本截取算法中采用实时线路柔性截取法，能够满足任务负荷的车辆配送里程最小化。算法完成后，可能出现两种情况：（1）车辆数过大。在车辆数充足时，可能最后一辆车在户数和货量上任务都过少；或者在所有车辆分配完成后，由于经验线路剩余少量零售户和货量，必须加派车辆。（2）工作量失衡。某些车辆在货量上满足标准装载量窗口要求，但零售户过少；或者零售户数量上满足标准户数窗口要求，但货量过少。

为最大程度提高车辆利用率，降低管理成本，减少上述两种情况的发生，在基本截取算法的基础上进行算法改进，增加“装载最大化”和“任务均衡化”两个处理过程。

（1）装载最大化

以k部候选车辆的标准参数上限U_SW和U_SC为条件执行硬性截取算法，得到最优车辆数k0。

（2）任务均衡化

若执行装载最大化操作后，经验线路上仍有剩余，说明可用车辆数不足，程序结束。否则，在不增加车辆的前提下，循环多次调节车量标准装载量窗口和标准客户数窗口的上限和下限后执行基本柔性截取算法，使车辆的任务满载率均衡化。在调节过程中需保证分配车辆数不大于k0，且配送里程增量最小化。

设窗口压缩调节次数为Times，且第m次调节时，窗口宽度为r。当m较小时，参数窗口的上限较大，有利于保证车辆数最少；当m较大时，参数窗口的宽度较小，有利于保证工作量均衡化。 当r较大时，参数窗口宽度较大，有利于保证配送里程最小化；反之，当r较小时，参数窗口宽度较小，有利于保证车辆数最少。为保证结果的最优化r的取值范围为[0，Times-1]，m的取值范围为[1，Times]。

2.4 算法主要技术思路以及创新点

卷烟配送线路为从物流公司出发，经过配送范围内的所有零售户节点，然后返回物流公司的行程。不少学者虽然提出了构造算法、两阶段法、蚁群算法、粒子群算法、混合算法、遗传算法、禁忌搜索算法、神经网络、模拟退火等方法，然而这些算法迭代速度缓慢、计算耗费时间长，可推广性和适用性一般[3-9]。针对这些缺陷，本文提出了一种改进的柔性线路截取优化算法（简称FOIA算法），宏观上综合权衡装载量以及配送户数，微观上进行配送节点逐点调整以及多点交换，建立了“以量定车，以户定线，户量均衡，动态优化”的弹性送货新模式。采用此种方法进行优化，既解决了现有算法存在的缺陷，又在较大程度上增强了获取最优解的可能性，具有很强的现实应用价值。

2.4.1 主要技术思路

算法主要技术思路：（1）逐点调整，即对已有配送线路中的各节点进行位置调整，如果节点调整位置后总路程减少，则用节点新位置替代原节点位置，并进行不断的循环改进，直到对所有节点的位置调整均不能减少总路程为止。（2）多点交换，逐点调整仅能调整邻近节点位置的缺陷，利用结构体状态集合穷举可调整任意多个节点的位置，从而使得优化结果计算更加快速高效。（3）交替使用，即交替使用逐点调整法以及多点交换进行计算，并增加配送节点调整及交换随机因子，能够快速得出更优的节点顺序，保证启发算法结果的完整和高效。（4）适当控制，即通过适当控制迭代次数（搜索半径），能够较快地完成线路划分，将全部客户合理分配给各配送线路，并保证各线路内部遍历路径较短。（5）有效结合，统筹考虑结合局部最优以及全局最优，避免出现最临近法构造线路存在的运算时间增长，散点数量增加和分布分散的不足，也可以克服遗传算法、禁忌搜索算法、神经网络、模拟退火等启发式算法无效迭代（搜索）过多导致计算耗费时间长的缺陷。

2.4.2 创新点

主要创新点有：（1）一种改进的柔性线路截取优化算法，综合进行配送节点逐点调整以及多点交换完成线路优化。（2）建立了“以量定车，以户定线，户量均衡，动态优化”的弹性送货新模式，打破了以往行政区划以及配送区域的概念，支持随访随销，较大程度地提高了配送方案调整能力、配送计划变更能力、协同配送能力和配送策略灵活性。（3）提出了“以量定车，以户定线”的思路，并综合权衡装载量以及配送户数，实现配送线路动态优化。（4）优化已分配给线路的全部客户的访问次序，生成线路客户最优或近似最优的排序序列。（5）使用相应的管理手段来保障和提升线路优化结果，形成一个完整性的物流配送线路动态优化体系和全面有效的配送监管机制，实现技术与管理的相辅相成。

2.5 算法分析及运行效果

2.5.1 收敛性与复杂度分析

本文算法（FOIA算法）从问题的状态空间中随机选取的可行初始解着手，采用改进的迭代运算，逐步逼近问题的最优解。

收敛性分析方面，FOIA算法所求解目标问题的状态空间S是有限集，算法的运行过程是随机过程，并可以用马尔可夫链来表示。FOIA算法的寻优过程的状态转移概率以概率1收敛于全局最优解，算法收敛性证明如下：

定义1.设算法在第t次迭代时结构体状态集合为X（t）={xt,i…,xt,n}，其中xt,i S, n＜∞，x和S分别表示可行解向量和解空间，n为结构体中搜索元的个数。{X(t)，t＞ 0}构成一个离散时间的随机过程，其状态空间为E=|S|n。

定义2.算法优化问题的全局最优解集合为E*=令表示结构体中包含的最优解的个数。

定义3.若对任意初始状态X0均有则称FOIA算法以概率1收敛于全局最优解。

定理1. FOIA算法寻优过程{X(t),t＞ 0}是有限齐次马尔可夫链。

证明：令t=0，结构体状态集合随机产生初始状态X(0)={x0,1，x0,2…,x0,n}。之后迭代遍历计算过程中，算法会基于当前结构体状态集合记忆的信息搜索解的空间, 并更新结构体集合状态。设t时刻结构体的状态为X(t),t+1时刻结构体的状态为X（t+1），解的空间使结构体集合状态以概率P(X(t+1) |X(t))转移至t+1 状态，P(X(t+1) |X(t))依赖于X(t)且是一个与时间无关的常量：

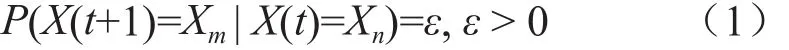
公式（1）中，Xm和Xn表示两个任意的结构体状态，所以{X(t),t＞ 0}有齐次马尔可夫性质。因为结构体集合状态有限，这样状态转移构成的马尔可夫过程的状态空间有限, 所以算法寻优过程{X(t),t＞ 0}是有限齐次马尔可夫链。

定理2. FOIA算法的结构体状态集合中最优解个数序列是不递减且单调的，即t ≥ 0，有

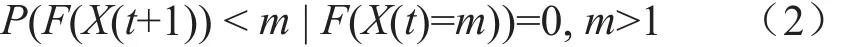
证明：因为最优解的路径结果距离值小于其他搜索结果，而算法的选择策略为留存任意时刻的最优解结果，所以迭代计算中上一轮的结构体状态集合中最优解肯定在新一轮结构状态集合体中，即在任意t时刻结构体状态集合中最优解的个数为k（k ＞ 0）的条件下，t+1时刻结构体中最优解的个数小于k的概率是0。

定理3. FOIA算法计算过程中在任意时刻t都会得到全局最优解, 即

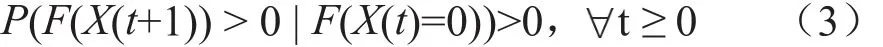
证明：根据FOIA算法的计算过程可知，全局优化路径在全部计算空间中是随机生成，所以任意t时刻全局计算结果为任意可能解的概率不为0，那么任意t时刻全局计算结果为全局最优解的概率也不为0。所以在迭代计算中上一轮的结构体状态集合中最优解的个数为0的情况下，新一轮结构状态集合体中最优解的个数不为0的概率大于0。

定理4. FOIA算法以概率1收敛于全局最优解，即有

证明：设Pr(t)=P(F(X(t))=r)表示t时刻结构体状态集合中最优解的个数为r的概率，根据贝叶斯条件概率公式有

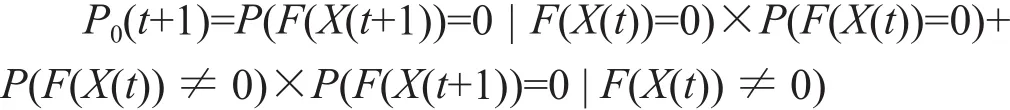
根据定理2有：P(F(X(t+1))=0 |F(X(t))≠0)=0，所以

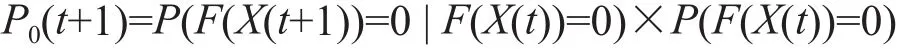
又根据定理 3得出：P(F(X(t+1)) ＞ 0 |F(X(t))=0) ＞0， 设，φ=min(P(F(X(t+1)) ＞ 0 |F(X(t))=0)?,t=0,1,…),则有

根据公式（5）可知：

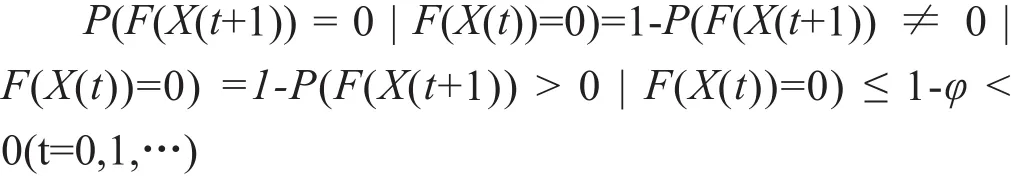
因此由于且故当 t→∞时有所以，因此，综上所述

所以

时间复杂性分析方面，给出FOIA算法的期望收敛时间的估算。

定义4.设算法可以表示的马尔可夫过程和最优状态空间若μ是一个随机非负整数的变量且满足：当且当，则称μ为算法收敛时间，μ的期望E(μ)称算法的期望收敛时间。

定义5. 对于任意t时刻，设马尔可夫过程和最优状态空间τ是一个随机变量且满足：当t=τ时 ,{η(t)∈E*；当 0≤ t ＜τ 时，{η(t)∈E*，则称τ的期望E(τ)是首次获得最优解的期望时间。

引理1. FOIA算法的收敛时间μ等于首次获得最优解的期望时间τ。

证明：对于任意t时刻，当t=τ时 ,η(t)∈E*。因为是吸收态马尔可夫过程，则又因为P{η(t)∈E*}=1 ，所以P{η(τ+1)∈E*}=1。同理可证，当t＜τ时，P{η(t)∈E*}=1.根据定义5，当t＜τ时 ,P{η(t)∈E*}＜1 根据定义 4,有μ=τ。

定理5.设马尔可夫过程和最优状态空间其期望收敛时间是

证明：对于任意t时刻，有

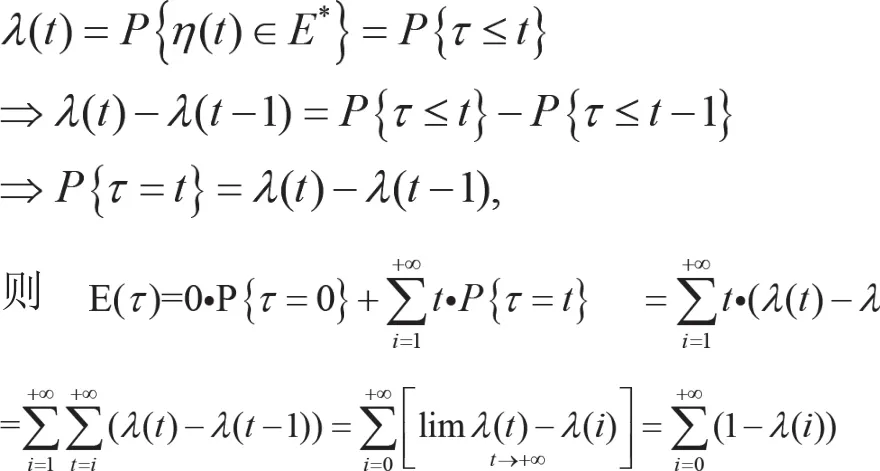
根据引理1，有

假设总共有m辆车，客户数量为n，i表示最大迭代次数，算法搜索过程划分为几个步骤:初始化所有客户两两之间的距离以及车辆信息参数的时间复杂度为O（n2+m）;构造结构体状态集合及更新解的空间时间复杂度为O（n2m），清空结构体状态集合的时间复杂度为O（nm）。使用时间复杂度的渐进表示法，则FOIA算法总的时间复杂度为T（n）=O（i×n2×m）。

空间复杂性分析方面，假设总共有m辆车，客户数量为n，则FOIA算法总的空间复杂度为S（n）=O（n2）+O(n×m)，具体分析如表1所述。

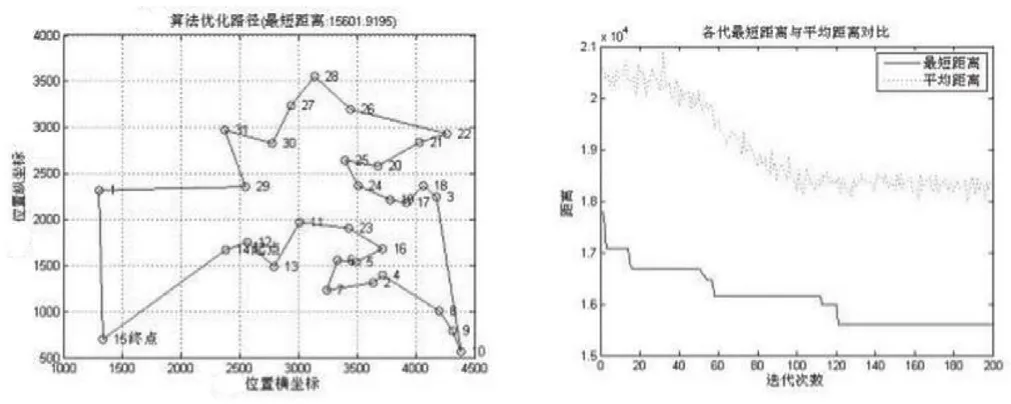
图2 算法MATLAB实验结果图Fig.2 Algorithm experiment result diagram by MATLAB tool

2.5.2 运行效果

FOIA算法打破了以往行政区划以及配送区域的概念，使物流配送管理能够主动地适应变化，并在漳州烟草物联网系统中成功实现，较大程度上降低了配送里程，节约了成本。配送线路变化详细如图3所示：

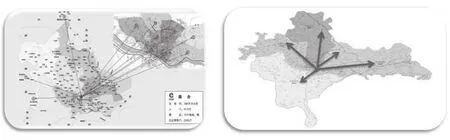
图3 配送线路前后变化示意图Fig.3 Sketch map of distribution line before and after distribution

2.6 弹性送货模式应用成效

弹性送货模式算法在漳州物联网系统实现并投入运行5年来，在周配送户数从25000户增加到30000户，卷烟销量从19万多箱增加到24万多箱的情况下，实现了送货车辆、配送人员减少、装载量及送货户数增加的效果，实现了提高卷烟配送效率、降低配送成本的建设目标，主要效果有：（1）配送日常使用车辆从79部减少到62部，配送车数下降了21.5%；（2）送货员工人数由158人减少至 124人，用工人数下降了21.5%；（3）单车日均配送量由49件增加到 74件，增加了 51%；（4）单车日均送货户数由 63户增加到97户左右，增长了 53.9%；（5）卷烟单件配送成本由244元 /箱下降为 189元 /箱，下降了 22.5%。

3 结论

本文分析了配送线路优化问题,针对这些问题给出了相应的解决思路,并阐述了柔性配送线路优化算法以及改进措施。此外，本文算法在漳州烟草物联网系统中成功实现。

漳州烟草打破以往行政区划以及配送区域的概念，建立了“以量定车，以户定线，户量均衡，动态优化”的弹性送货新模式，使物流配送管理能够主动地适应变化，增强自身在动态环境和过程中的竞争性，缩短响应时间，提升服务质量。5年的实际应用表明，在周配送户数从25000户增加到30000户、卷烟销量从19万多箱增加到24万多箱的情况下，送货线路却从79条减少到62条，在企业经营降本增效上取得了良好的成效。

[1]王勇,池洁，樊建新. 基于遗传算法的烟草物流配送区域划分优化研究[J]. 重庆交通大学学报(自然科学版)，2009，28(3):619-621.WANG Yong, CHI Jie, FAN Jianxin, Optimization of cigarette logistics deliver region partition based on genetic algorithm [J].Journal of Chongqing Jiaotong University (NATURAL SCIENCE EDITION), 2009, 28 (3):619-621.

[2]徐智，陈军，唐萍. 卷烟商零物流动态线路优化和在途监控的研究及实现[J].中国烟草学报， 2014, 20(1)：71-73.XU Zhi, CHEN Jun, TANG Ping. Study of dynamic route optimization and monitoring in cigarette distribution [J]. ACTA TABACARIA SINICA, 2014, 20(1):71-73.

[3]Taniguchi E, Noritake M, Yamada T, et al. Optimal size and location planning of public logistics terminals[J]. Transportation Research Part E: Logistics and Transportation Review, 1999, 35(3): 207-222.

[4]Bramel J, Levi D. A location based heuristic for general routing problems [J]. Loca tion Science, 1997, 5(1): 60-60.

[5]Fuellerer G, Doerner K F, Hartl R F, et al. Ant colony optimization for the two-dimensional loading vehicle routing problem[J].Computers & Operations Research, 2009, 36(3): 655-673.

[6]Goksal F P，Karaoglan I，Altiparmak F. A Hybrid Discrete Particle Swarm Optimization for Vehicle Routing Problem with Simultaneous Pickup and Delivery[J].Computers & Industrial Engineering，2013, 65(1): 39-53.

[7]Morais V W C，Mateus G R，Noronha T F. Iterated Local Search Heuristics for the Vehicle Routing Problem with Cross-Docking[J].Expert Systems with Applications，2014, 41(16).

[8]胡红春，吴耀华，廖莉. 物流配送车辆线路的优化及其应用[J].山东大学学报(工学版)，2007, 37(4):104-107.HU Hongchun, WU Yaohua, LIAO Li. Routing optimization for logistics distribution and its application [J]. Journal of Shandong University (ENGINEERING SCIENCE), 2007, 37(4):104-107.

[9]Cheikh M, Ratli M, Mkaouar O, et al. A Variable Neighborhood Search Algorithm for the Vehicle Routing Problem with Multiple Trips[J].Electronic Notes in Discrete Mathematics，2015, 47 : 277-284.