直流互击式喷注器的实验与数值研究

李子阳，李家春，刘 忠

0 引 言

火箭喷注器是火箭发动机的核心部件，可以将推进剂进行雾化和混合后输入到燃烧室内，直接影响发动机的推进剂雾化混合效果，决定了其工作性能。直流互击式喷注器在机械加工时的喷注角度、腔道深度以及喷孔的分布等导致了喷注器内部流场较为复杂，因而产生能量损失大、流量分布不均匀等问题。随着计算流体力学（CFD）和计算机技术的快速发展，对喷注器的三维数值模拟已成为可能，具有可重复性、条件容易控制的特点。对直流互击式喷注器的流场研究主要以喷孔喷出后的流场特性为主，如，李佳楠等[1]实现了对直流互击式喷注器喷注单元雾化过程的准直接数值模拟；刘昌波等[2]开发了一种雾化过程的多尺度仿真算法，与实验对比分析表明，所开发的算法可以实现雾化仿真模拟。而针对直流互击式喷注器内部流道流场的数值模拟还未进行，由于直流互击式喷注器在实验过程中对某些参数无法精确测量，对喷注器内部流道存在的问题也无法深入分析。本文采用 Fluent软件来对两股互击式喷注器的内部流道流场进行模拟分析并通过实验进行了验证。

1 直流互击式喷注器的物理模型

直流互击式喷注器由喷注器法兰、分流板和喷注面板构成。分流板与喷注面板嵌入法兰，分流板上的扩散焊肋与法兰形成集液腔体，喷注面板与分流板形成分配腔，喷注面板上有多对喷嘴。燃料和氧化剂通过法兰上对应的进口以一定的流量进入集液腔再进入分配腔，最后由喷孔喷出。喷注器装配结构如图1所示。

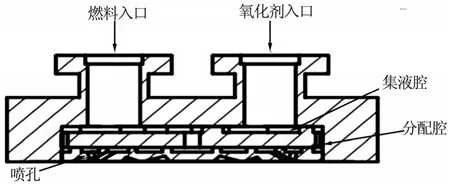
图1 直流互击式喷注器装配结构示意Fig.1 Illustration of Assembly Structure of DC Impact Injection Device

直流互击式喷注器流道三维模型如图 2所示。图2a中，左边为燃料路，右边为氧化剂路。燃料路出口由内向外依次为第1圈、第2圈、第3圈和冷却孔；氧化剂路出口由内向外依次为第1圈、第2圈和第3圈。每一圈孔的编号如图2b编号所示，圈孔逆时针开始。由于燃料和氧化剂在喷注器内是两个不同的流道，所以本文分别对燃料路和氧化剂路进行了数值模拟。

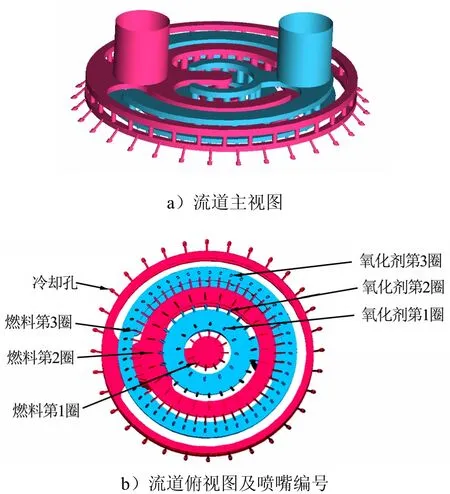
图2 直流互击式喷注器流道示意Fig.2 DC Injection Injector Flow Channel

2 直流互击式喷注器内部流道的数学模型

喷注器内部的液流为常温下粘性不可压缩流体，液体在流道内多处为湍流流动，忽略流体的温度等能量传递，采用标准k-ε湍流模型控制方程[3]且不考虑能量方程，具体数学模型如下：

连续方程：

式中 u，v，w为速度矢量在x，y，z方向的分量。

动量（N-S）方程：

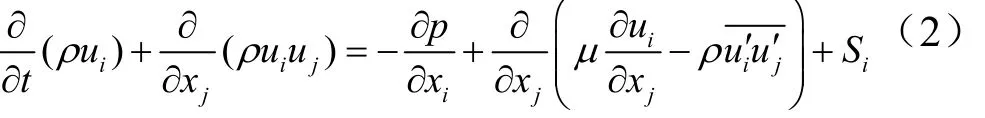
式中 ρ为流体密度；ui，uj分别为平均速度，i=1,2,3，j=1,2,3；p为瞬时压力；μ为动力黏度；-为雷诺应力项； Si为源项。

标准k-ε方程：

式中tu为湍流黏度；uC为经验常数；k为湍动能；z为湍动耗散率。

湍动能k的运输方程：

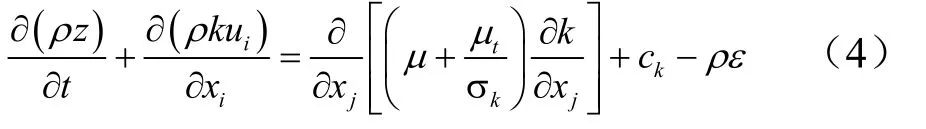
式中kc为平均速度引起的湍动能 k的产生项，；σk为经验常数，σk= 1；t为时间； xi, xj为空间坐标；ε为耗散率。

耗散率ε的运输方程：

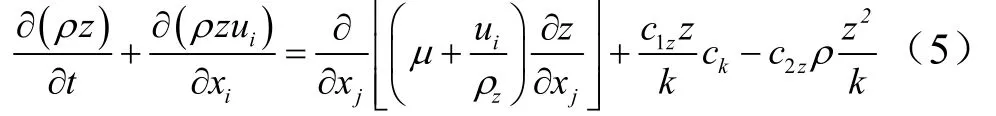
式中1zc，2zc，zσ为经验常数，1zc=1.44，2zc=1.92，zσ=1.3。

3 网格划分与边界条件

用ICEM CFD 对流道进行网格划分，由于几何体结构较为复杂，所以将几何体分成多个部分，对流道入口、管壁、集液腔壁、分配腔壁、喷孔壁、喷孔出口各个部分设置合适的网格尺寸。

利用“Robust”方法生成“Tetra/Mixed”类型的网格，经过多次验证，当网格数量超过300万时，仿真结果精度并无明显提高，反而会增加计算时间，所以网格数量应控制在300万左右，如图3所示。

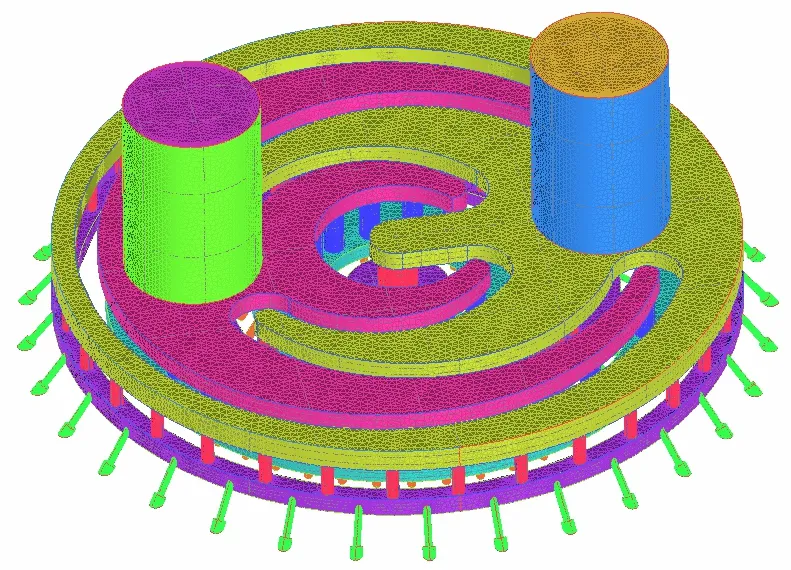
图3 网格划分示意Fig.3 Mesh Division

由于实际冷试车使用液态水进行液流实验，为了方便跟实验数据对比，将计算工质按照密度比，把额定燃料和氧化剂的流量换算成额定水的流量。将两个流道的入口均设置成质量流量入口，出口为压力出口，具体设置如表1所示。

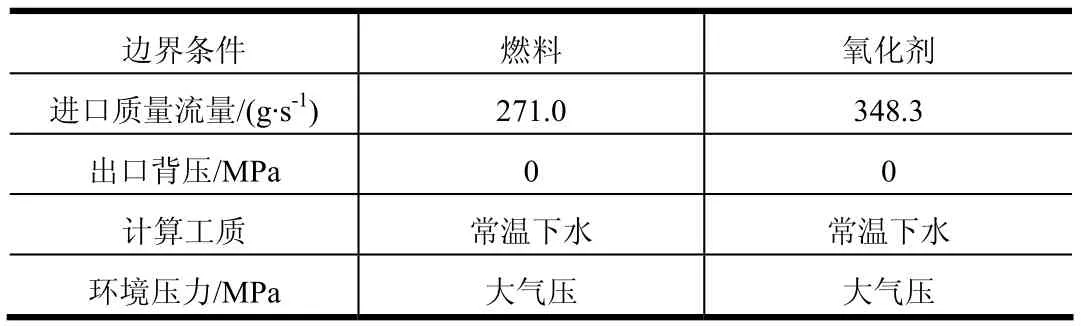
表1 计算边界条件Tab.1 Calculate Boundary Conditions

续图4

4 SIMPLE算法与模拟结果分析

SIMPLE算法是三维流体流场数值模拟的重要方法，在不同三维流体湍流流场模拟中取得了较好的应用[4～6]。本文采用SIMPLE算法对控制方程进行数值求解，简单地说，SIMPLE算法可以先假定一个压力场（或者上一次迭代的压力场），求解离散形式动量方程，得到速度场，再对压力场进行修正，接着根据修正后的压力场求得新的速度场；然后检查速度场是否收敛，若不收敛，开始进行下一层次的计算，直至收敛为止。

用有限体积法对控制方程进行离散，运用 Simple算法对控制方程进行数值求解，在跌代过程中收敛。

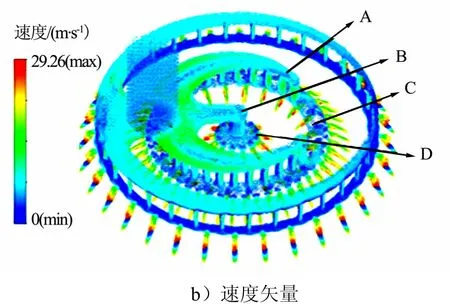
对计算结果进行处理，分别得到燃料路和氧化剂路的压力场和速度矢量云图，并由速度矢量云图得到单孔的流量折线图，如图4所示。

由图4a可知，燃料路的流道的总压降为0.50 MPa，从进口到集液腔的平均压降为0.03 MPa，在集液腔内的平均压降约为 0.10 MPa，在分配腔内的平均压降约为0.07 MPa，从喷孔前端到出口的平均压降为0.30 MPa，说明压降的产生跟流道的空间变化有密切的关系，且喷孔前压降主要存在于集液腔到出口的流道。

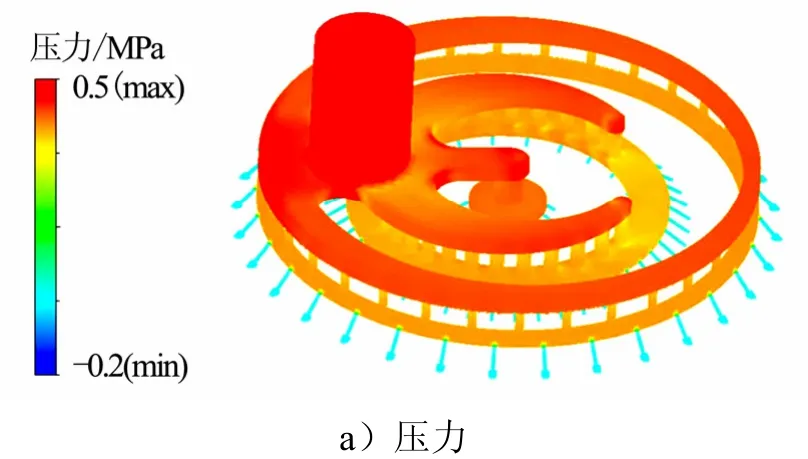
图4 燃料路流道数值模拟云图Fig.4 Fuel Flow Path Numerical Simulation Cloud Diagram

由图4b可知，液体从进口流入集液腔时速度增大，燃料流道内的最大速度为29.26 m/s，集液腔的4条流道的速度几乎均等，局部放大如图5所示。

图5 燃料路流道速度矢量局部放大示意Fig.5 Partial Enlargement of Velocity Vector of Fuel Flow Path

集液腔内的液体在每个通往分配腔的入口处都出现了液流回流的现象，液流在A和A的对称处（见图5a）产生了明显的相同涡流，并且在液流经过B处（见图5b）时产生了较大的涡流，消耗了这3处的主流运动的能量，从而使这3处出现了低压力区域。在分配腔的压降主要是由于每个通往喷嘴的入口处都形成了相似的涡流如C和D处（见图5c、图5d），由于产生了很多涡旋，涡旋内的反向回流与主流运动混合在一起，加剧了液流能量的损失，并且由于集液腔涡流的作用使得分配腔内圈远离入口部分压力较低且由于内圈涡流的相互作用，导致了如图6所示的第2圈孔的流量较低且分布不均匀。

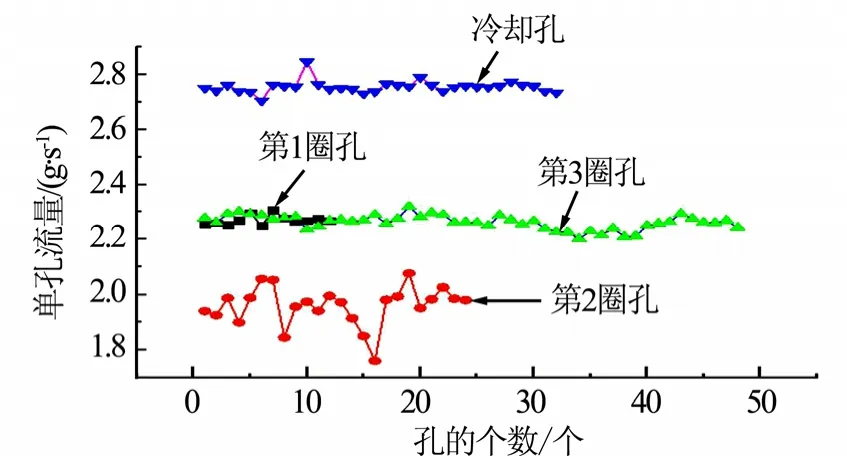
图6 燃料单孔的流量折线示意Fig.6 Fuel Single Hole Flow Fold Line

氧化剂路的压力场和速度矢量模拟如图7所示。

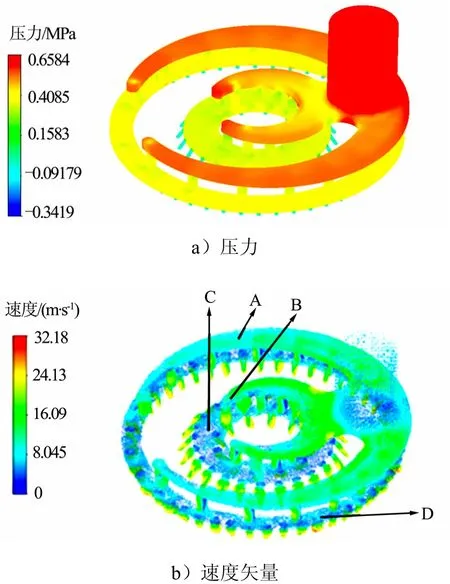
图7 氧化剂路流道数值模拟云图Fig.7 Oxidizer Flow Path Numerical Simulation Cloud Map

由于氧化剂路与燃料路在各部分流道结构相似，因此模拟结果也相似。由图7a可知，氧化剂路流道的总压降为0.64 MPa，从进口到集液腔的压降为0.09 MPa，液流在集液腔的平均压降约为0.12 MPa，在分配腔内的平均压降约为0.11 MPa，从喷孔前端到出口的平均压降为0.32 MPa。压降主要存在于集液腔到出口的流道。由图7b可知，氧化剂流道内的最大速度为32.18 m/s，液体速度变化与氧化剂路相似。集液腔与分配腔产生压降的原因与燃料路相同，都是由于在腔道内产生了涡流，如图7b的A、B、C、D处（局部放大如8所示）。由图8可知，氧化剂路与燃料路主区别是涡流相互影响较大，使得分配腔内圈压力分布不均，导致如图 9所示的第1圈孔的流量、第3圈孔的流量波动较大。

图8 氧化剂路流道速度矢量局部放大示意Fig.8 Oxidation Flow Path Velocity Vector Partial Enlargement

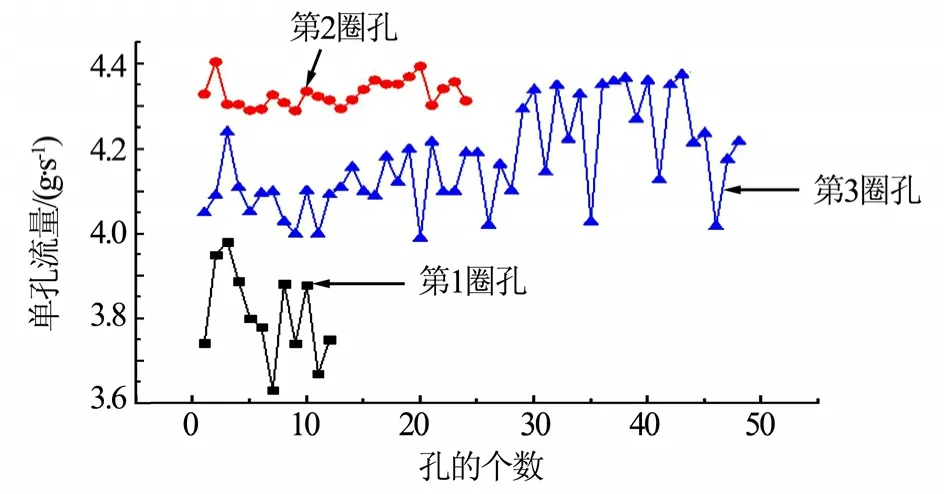
图9 氧化剂路的单孔流量折线示意Fig.9 Single Hole Flow Line of Oxidizer

5 实验验证

由于实际推进剂在实验时成本高且具有一定的危险性，所以为了方便和仿真进行了对比。实验研究以液态水作为推进剂替代工质，实验系统主要由高压气瓶、管路、贮水箱、流量计、压力测量仪、流量测量工装和直流互击式喷注器组成。高压气瓶中的氮气经过减压后进入水贮箱，给液态水加压，水经过流量计、喷注器前测压表后进入喷注器。通过调整减压阀来改变喷注器前的压力，通过流量计来测量喷注器流量。实验通过测量喷注器水流量与压降的关系，拟合出函数关系式，从而算出额定水流量下的压降，并将其作为喷注器数值模拟的校验依据。分别对燃料路和氧化剂路进行了实验，各自获得10个压力差下的流量。实验测量结果如图10所示。

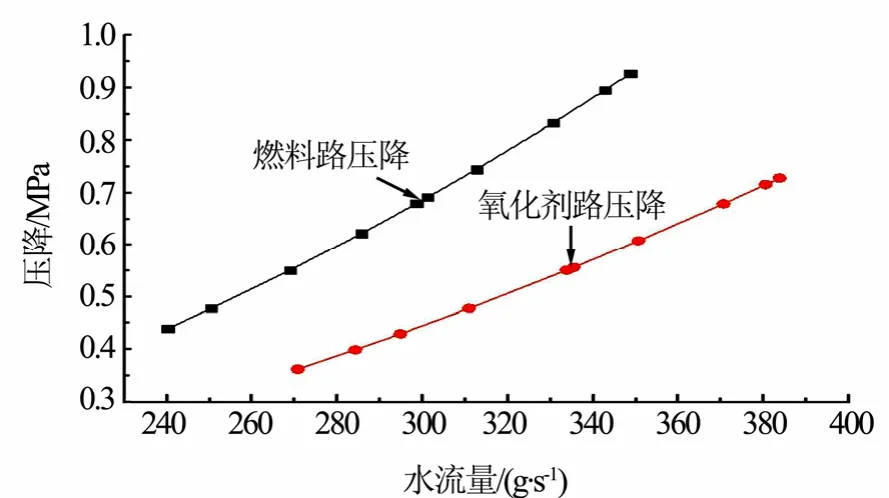
图10 测量结果的函数示意Fig.10 A Function of the Measurement Result

求出的其函数关系式如下：

燃料路：y=7.625169×10-6x2；

氧化剂路：y=4.945888×10-6x2。

式中 x为水流量；y为压降。不难发现，压降与流量的平方根存在着线性关系，关系式可以转成理论公式形式，即：

式中 a为常数。

将额定水流量代入式（6）求得燃料路额定水流量的压降为0.56 MPa，氧化剂路额定水流量的压降为0.60 MPa，仿真得到的燃料路额定水流量压降为0.51 MPa，氧化剂路额定水流量压降为0.64 MPa。经过对比发现，仿真燃料路压降比实际压降低0.05 MPa，占8.9%；仿真氧化剂路压降比实际压降高0.04 MPa，占6.7%。考虑到实际测量设备存在测量误差以及数值模拟中存在着计算误差，说明数值模拟结果符合测量结果。

为了对数值模拟进一步验证，本实验利用流量测量工装对燃料路各圈各单孔流量进行测量，并将实验测量燃料路单孔流量与数值模拟的燃料路单孔流量进行对比，如图11所示。

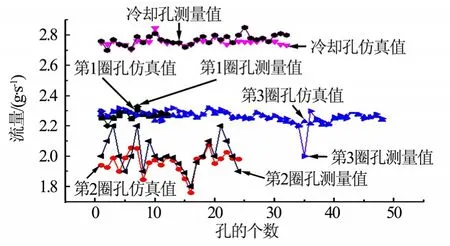
图11 燃料单孔流量对比示意Fig.11 Single Hole Flow Comparison of Fuel

由图11可知，数值仿真的流量值的变化规律与实验测量值吻合较好。

6 结 论

本文对直流互击式喷注器开展了冷态实验和数值仿真研究，结论如下：

a）模拟结果与实验结果吻合较好，说明数值模拟方法正确。从数值分析结果来看，燃料路从喷孔前端到出口的平均压降约占总压降的 60%，氧化剂路从喷孔前端到出口的平均压降约占 50%。由于喷孔前端到出口处的压降决定了液体喷出的速度，所以可以通过调整集液腔和分配腔的高度在尽量保证不增大压降的前提下尽可能增大喷孔前端压降，使得雾化的效果更佳。

b）数值分析结果表明，燃料路的第2圈孔的流量较低且分布不均匀，氧化剂路的压力分布和液流速度的稳定性低于燃料路，使得流量分布也不如燃料路均匀。可以通过改变分流板扩散焊肋的偏心距以及改变个别小孔的孔径来改善压力分布和单孔流量。

[1] 李佳楠, 费俊, 杨伟东,等. 直流互击式喷注单元雾化特性准直接数值模拟[J]. 推进技术, 2016, 37(4)： 713-725.

Li Jianan, Fei Jun, Yang Weidong, et al. Quasi-direct numerical simulation of atomization characteristics of DC impact injection unit[J].Advance Technology, 2016, 37(4)： 713-725.

[2] 刘昌波, 雷凡培, 周立新. 两股湍流射流撞击雾化过程的数值研究[J].推进技术, 2014, 35(12)：1669-1678.

Liu Changbo, Lei Fanpei, Zhou Lixin. Numerical study on impact nebulization process of two turbulent jets[J]. Advance Technology, 2014,35(12)：1669-1678.

[3] 李海龙, 高殿荣. 基于 Fluent液压集成块内部流道流场的数值模拟[J].液压与气动, 2011(3)：1-4.

Li Hailong, Gao Dianrong. Numerical simulation of flow field in internal flow channel of fluent hydraulic manifold[J]. Hydraulic & Pneumatic,2011(3)：1-4.

[4] 赵国智, 孔凡让, 占惊春, 张志伟, 柴华. 基于 SIMPLE算法的湍流场数值模拟[J]. 水电能源科学, 2007, 25(3)：100-102.

Zhao Guozhi, Kong Fanrang, Zhan Jichun, Zhang Zhiwei, Chai Hua.Numerical simulation of turbulent flow field based on SIMPLE algorithm[J]. Journal of Hydroelectric Energy Science, 2007,25(3)：100-102.

[5] 李进贤, 岳春国, 侯晓, 冯喜平. 针栓式变推力火箭发动机内流场数值仿真研究[J]. 计算机仿真, 2009(8)： 49-52.

Li Jinxian, Yue Chunguo, Hou Xiao, Feng Xiping. Numerical simulation of internal flow field in pin-poke type thrust rocket engine[J]. Computer Simulation, 2009(8)： 49-52.

[6] 陈杰. 喷注器流道解析解和数值解[J]. 宇航学报, 1990(4)： 97-102.

Chen Jie. Analytical solution and numerical solution of injector flow path[J]. Journal of Astronautics, 1990(4)： 97-102.