基于质量阵Cholesky分解的发动机悬置系统优化
2018-07-05,
,
(内蒙古工业大学 能源与动力工程学院,呼和浩特 010051)
1 引 言
为了减少发动机激励源对车身的振动,除了通过合理布置曲柄间相互位置、采取有效平衡方法和点火顺序来消除或减少干扰外,还应采取隔振措施来减小发动机传给车身的干扰力。恰当选取支撑参数不仅可使整车振动及噪声水平明显下降,而且能防止发动机过早损坏,提高车上各零部件的疲劳寿命,为此在现代汽车设计中,发动机悬置系统的设计受到广泛重视。动力总成悬置系统设计的任务就是确定刚度阵。若将已知发动机悬置系统的振动微分方程,求发动机悬置系统的固有频率和振型看作是正问题,那么给定系统的振型及固有频率,求刚度矩阵则成了上述正问题的逆问题[1-5]。
设计发动机悬置系统的目的就是为了防止发动机激振力向车身传递,使悬置起到隔离振动的效果,设计时发动机型号已知,质量阵便已确定。从隔振的角度,汽车发动机悬置系统的固有频率通常为设定值,如何选取合适振型(模态),就成为设计的关键。文献[6]对汽车发动机悬置系统进行了多目标优化,文献[7]应用区间分析的方法对发动机悬置系统进行稳健优化设计,文献[8]应用模拟退火算法对全地形车发动机悬置系统进行参数优化,文献[9,10]则分别应用粒子群算法和遗传算法对汽车动力总成悬置系统作了优化设计,还有针对车辆耦合振动系统,基于状态空间分析的优化方法等[11,12]。
本文提出了广义坐标下,基于质量矩阵的Cholesky分解来设计正则模态矩阵,进而对发动机悬置系统进行优化求解的方法。
2 悬置系统的振动微分方程
动力总成是汽车最大的集中质量,为了有效隔离发动机引起的振动,动力总成与车身通过弹性支撑元件相连,动力总成与弹性支撑元件共同组成了发动机悬置系统。汽车发动机均采用多点弹性支撑,如图1所示。

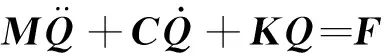
(1)


图1 发动机支撑
Fig.1 Engine mount
(2)
(3)
式中m为动力总成质量,J..为转动惯性矩和惯性积。以质心O点作为原点的惯性坐标系 {O-xyz},坐标轴与惯性主轴重合,此时惯性积为0,质量阵可对角化为
(4)
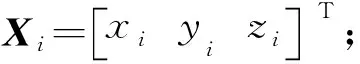
(5)

ΔWi=RiΔXi
(6)
式中Ri=Ru iRv iRs i,Ru i,Rv i和Rs i为安装角的旋转矩阵,得
(7)
ΔXi为发动机总成振动在弹性支撑Xi处的变形量,
ΔXi=X+RθXi-Xi
(8)
式中Rθ=RxRyRz为发动机总成的旋转矩阵,与式(7)相似,而Rx,Ry和Rz亦为正交旋转矩阵,限于篇幅不再给出。只研究微小转动时,cosθ≈1,sinθ≈0,式(8)化为
(9)
将式(9)代入式(8)可得
ΔXi=X+(Rθ-I3 × 3)Xi=
(10)

(11)

(12)

(13)
3 发动机的振动激励源分析
对于单缸发动机,在恰当的假设条件下,根据力学原理,把整套曲柄连杆机构的质量用集中在曲轴销与活塞销上的两个质量代替,如图2所示,r为曲柄半径,l为连杆长度;m1为曲轴等效质量,对支撑产生离心惯性力为Pr,在坐标轴上的分量为Pr x与Pr y;m2为活塞等效质量,除了对支撑产生往复惯性力Pj,活塞往复运动时,由于缸壁的压力PN,还会对支撑产生扭矩Mz c。

图2 单缸发动机运动部件及受力简图
Fig.2 Diagram of moving parts and force of single -cylinder engine
以简化中心C点(位于曲轴中心线上)作为原点的惯性坐标系{C-xcyczc}中,离心惯性力Pr等于质量m1的向心力,可以表示为
Pr=m1rω2
(14)
活塞的位移xc等于CA的长度,几何关系为
xc=r(cosα+1/λcosβ)≈
l(1-λ2/4)+r(cosωt+λ/4cos2ωt)
(15)
式(15)用到了几何关系sinβ=λsinα,且忽略了cosβ的泰勒展开式中二次以上的高阶项,λ=r/l为曲柄与连杆长度之比。式(15)中的位移对时间求两阶导数得
(16)
Pj=-m2rω2(cosωt+λcos2ωt)
(17)
式中 往复惯性力Pj由一次惯性力和二次惯性力两部分组成,若保留泰勒展开式中更高次高阶项,则有更高次的惯性力。活塞作往复运动时,会对缸壁产生压力PN,对连杆产生压力PT,由PN+PT=Pj+Pg,可推导出
PN=(Pj+Pg)tanβ
(18)
PN对zc轴产生扭矩Mz c为
Mz c=PNxc=r(Pg+Pj)sin(α+β)/cosβ
(19)
式中 发动机主动力Pg=(pg-1)S,S为气缸燃烧室面积,pg为缸内压强[13]。
图3给出四缸直列发动机的受力情况,可视为由曲轴连接起来的四个单缸发动机,作用力应是各个单缸体受到的干扰力组成的一组空间力系,
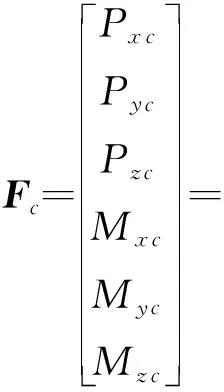
(20)
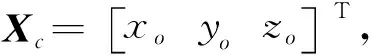
(21)
由式(21)可知,式(20)的一些惯性力理论上可以平衡掉,但在工程实际中,由于加工精度和装配等原因,这些惯性力仍会不同程度地存在;由于各气缸之间所经历的冲程不同,如图4所示,以发火顺序为1-2-4-3缸为例,作用于z轴上的扭矩不能平衡掉,故发动机主动力Pgi是引起发动机振动的最主要激励源。
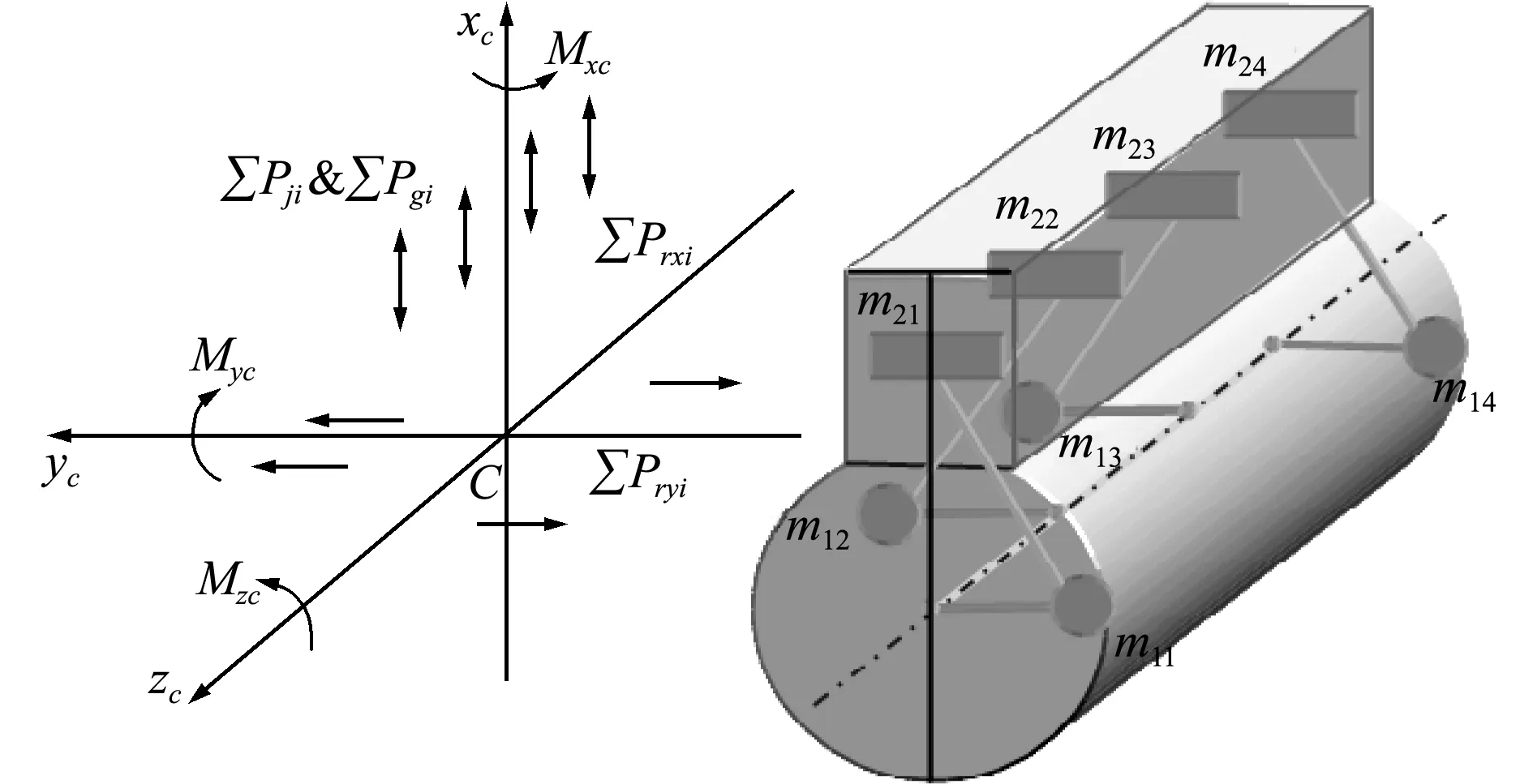
图3 直列四缸发动机受力情况
Fig.3 Four-cylinder engine force condition
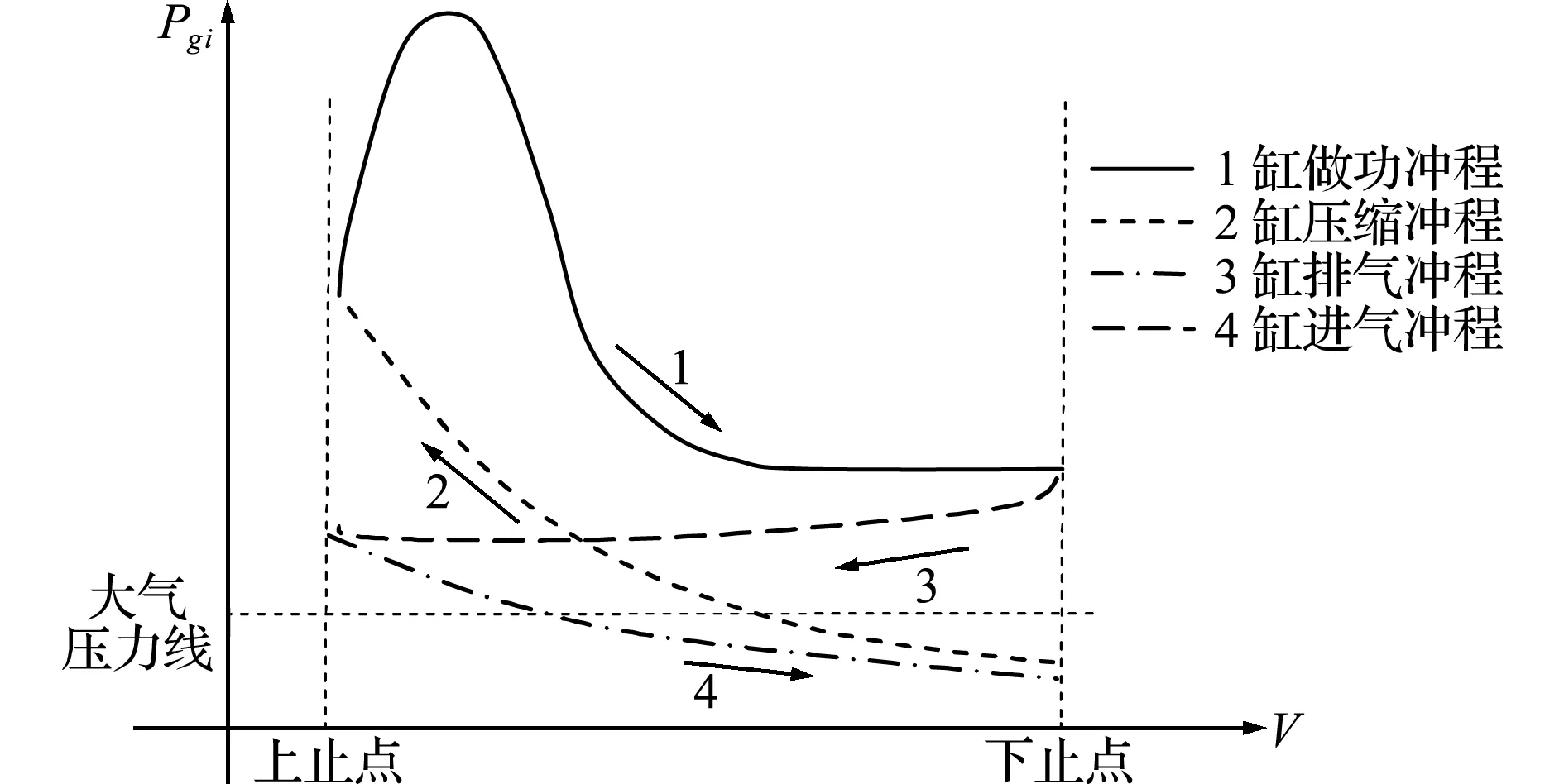
图4 四冲程发动机示功图
Fig.4 Four-stroke engine dynamometer
4 发动机悬置系统设计及优化
设计发动机悬置系统时,对于已给定的发动机,可通过一些简单的计算方法和测试手段获得以其质心为原点的惯性坐标系的质量矩阵M。如何选取恰当的支撑参数是设计的关键,这里又包含两个问题,即如何设计系统的固有频率与模态振型。系统的固有频率需满足工程实际需要,对于隔振,希望固有频率能够错开激励频率,且离激励频率越远越好,所以在设计时要求固有频率满足:
ωn 1,ωn 2,…,ωn 6∈(0ωd max]
(22)
ωd max为设计的固有频率上限。若以广义坐标表示振动Qc=[w1w2w3w4w5w6]T,假设有如下关系,
Q=EQc
(23)
式中E为坐标间的变化矩阵,非奇异,可推得
(24)
(25)
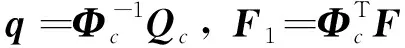
此时实模态解耦,K1称为谱阵。由式(24)可知
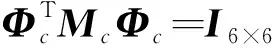
(26)
式(26)表明,可用矩阵Mc的Cholesky分解来设计正则模态矩阵,则物理坐标下的正则模态矩阵为
Φ=EΦc=[φ1φ2…φ6]
(27)
Cholesky分解又叫三角分解,是对称正定矩阵最常用的分解方法之一,且这种分解是唯一的[13,14]。若给定系统的固有频率,则谱阵K1为

(28)
由式(27,28)可得
(29)
对照式(12,29)可反解出支撑参数为
(30)
式(26)中质量矩阵不用M的原因为该质量矩阵本身是对角阵,Cholesky分解也必然是对角阵,将导致式(28)的刚度阵K也为对角阵,最终反解出的支撑参数在工程中无法实现,这也是引入广义坐标来表示振动的原因。坐标间变化矩阵的选取具有一定的设计主观性,可根据式(10)的刚度矩阵耦合形式选取E。

(31)
由于刚度耦合的存在,一般情况下,发动机总成将沿多个广义坐标方向发生振动,传递给车身的振动也会表现在多个方向。式(31)中,ε一般为小值,ε取值越大,系统耦合越严重,因此称ε为耦合控制因子。在不考虑耗能的情况下,振动动能与势能之和为一常数,等于最大势能。当系统以第i阶模态振动时,设φi是固有频率ωn i对应的振型向量,最大振动总势能为
(32)
第j个广义坐标分配的势能占系统总势能的比例定义为
λi j=(Uij/Uitol)×100%
(33)
由式(33)可定义能量分布矩阵为
λ=[λi j] (j,i=1,2,…,6)
(34)
由能量分布矩阵定义可知,若追求发动机悬置系统的解耦,λ阵的各列只有一个元素趋于1而其他元素趋于0,工程中某元素达到90%以上即属于较好解耦。
对于单自由度振动隔离系统,输出与输入之间可以直接建立起传递函数,但对于六自由度系统,输出与输入之间建立的是传递函数矩阵,虽然矩阵中每个传递函数可以评估在这个自由度方向上的隔振效能,但整体的隔振效能无法评估,这里提出迹传递函数来评估整体的隔振效能。对式(1,25)作傅里叶变换:
Q(ω)= [K-ω2M+jωC]-1F(ω)=
H(ω)F(ω)
(35)
q(ω)= [K1-ω2I6 ×6+jωC1]-1F1(ω)=
H1(ω)F1(ω)
(36)
可验证H(ω)与H1(ω)的迹相同,
Htr(ω)= tr[H(ω)]=tr[H1(ω)]=
(37)
式中Htr(ω)称为迹动柔度函数,ζi为阻尼比。迹动柔度函数是解耦后6个单自由度系统的动柔度函数的线性叠加,可认为是单自由度动柔度函数的一种推广。发动机悬置本质上是多自由度动力隔振,类似迹动柔度函数,本文定义迹动力传递函数为
(38)
式中Fai和Fb i为解耦后各方向上隔振前后的力。
5 发动机悬置系统设计与优化实例及动力学仿真
针对某车企生产的BC306Z型乘用车的纵置发动机动力总成采用四点悬置系统,进行优化设计,悬置系统各参数列入表1,表中共有三类36个支撑参数,每类参数中各包含12个参数。应用式(4,12)不难求出系统谱阵K1=diag[7230 2512 1329 1389 9561 12589]。应用式(32~34)可求出能量分布矩阵λ,可见采用以上参数解耦情况较差。
表1 某四支撑发动机悬置系统参数
Tab.1 Parameters of a four-point engine mount system

质(惯)量(kg,kg·m2)m=136,Jx=7.70,Jy=8.78,Jz=3.74支撑参数主轴刚度×104(N·m-1)安装欧拉角(°)安装位置(m)ku1=ku2=2.5ku3=ku4=18.5kv1=kv2=2.5kv3=kv4=6.2ks1= ks2=8.8ks3=ks4=9.7θu1=-θu2=-40 θu3=θu4=5θv1=θv2=0θv3=θv4=-3θs1=θs2=0θs3=θs4=0x1=x2=-0.15x3=x4=-0.12y1=-y2=0.27y3=-y4=0.30z1=z2=0.54z3=z4=-0.28

讨论给定支撑安装位置,对支撑主轴刚度及安装欧拉角进行优化求解。优化的目的是实现系统解耦,且使得从发动机传递给车身的动力尽可能小,即优化后迹动力传递函数Ttra(ω)小于优化前Ttrb(ω)。因此这个优化问题的目标函数和约束条件描述为
∃max.[λi j]≥85% (j=1,2,…,6)∩
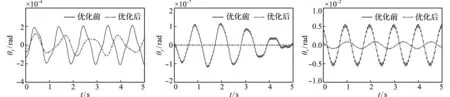
Ttra(ω) (39) 对于求解式(39)的优化问题,目前已有多目标优化方法、区间优化方法及模拟退火算法等多种方法。本文根据前文提出的基于广义质量阵Cholesky分解振型的优化策略对此进行求解。 当耦合控制因子ε=0.1时,det(E)=0.9496,矩阵E非奇异,利用式(24~29)求目标刚度矩阵K可得 由式(29)列出相关参数的线性方程组,矩阵形式写为 在最小二乘原则下,可对Di(i=1,2,3,4)进行求解。由旋转矩阵是正交矩阵的性质可得 (40) 由反解出的悬置系统支撑参数计算能量分布阵为 从能量分布矩阵λ可知,当耦合控制因子ε=0.1时,max .[λi j]≥85%(j=1,2,…,6),系统基本实现了解耦;当耦合控制因子选取更小值时,其解耦效果更佳。 图5给出了在MATLAB的Simulink中,利用本文优化实例中参数,根据式(4,12,13,21)建立的直列四缸发动机动力总成悬置系统的仿真模型,仿真时发动机转速为1200 r/min。 优化前后时域仿真对比结果如图6所示,可以看出,因为实现了解耦,在x,y,z和θy方向,优化后发动机的振动位移趋于0,优化前后较大的振动方向是θz和θx,优化后幅值也较优化前小。 表2 某四支撑发动机悬置优化后结果 Tab.2 Results of a four-point engine mount optimization 支撑主轴刚度×104/(N·m-1)ku1=ku2=1.8ku3=ku4=12.3kv1=kv2=3.8kv3=kv4=1.7ks1=ks2=3.7ks3=ks4=3.5支撑安装角/(°)θu1=-θu2=50θu3=-θu4=-43θv1=θv2=2θv3=θv4=0θs1=-θs2=-88θs3=θs4=0 图5 悬置系统的仿真模型 Fig.5 Simulation model of engine mount 图6 优化前后时域仿真结果对比(1200 r/min) Fig.6 Simulation results contrast before and after optimization (1200 r/min) 图7 迹动力传递函数优化前后对比 Fig.7 Transfer function contrast before and after optimization 应用式(37),在阻尼比ζi=0.1的情况下,图7给出了优化前后的迹动力传递函数对比,可以看出,优化后系统的6个固有频率有所降低,故由发动机传递给车身的动力也将减小。 通过对汽车动力总成悬置系统优化设计与动力学仿真研究,得到如下结论。(1) 可用广义坐标下质量矩阵的Cholesky分解来设计目标正则模态矩阵,但坐标间变化矩阵的选取具有一定的设计主观性,可根据刚度矩阵的耦合形式选取,并做出调整;(2) 基于广义质量阵Cholesky分解振型的优化求解关键在于对耦合控制因子的选取;(3) 根据目标正则模态矩阵计算的动力总成的刚度矩阵,与由反解出的支承参数计算的刚度矩阵,在最小二乘原则下,两者之间的误差最小,因而可以保证反解出的支承参数是优化的结果;(4) 发动机的振动位移优化后小于优化前,通过悬置系统的动力学仿真结果证明了优化方法的可行性及有效性。 : [1] 吴 杰,上官文斌,唐 静,等.动力总成悬置系统解耦布置的鲁棒性分析[J].振动与冲击,2009,28(9):15-20.(WU Jie,SHANGGUAN Wen-bin,TANG Jing,et al.Robust analysis for decoupling layout of a powertrain mounting system[J].JournalofVibrationandShock,2009,28(9):15-20.(in Chinese)) [2] 李志强,陈树勋,韦齐峰.发动机总成悬置系统解耦方法研究[J].动力学与控制学报,2013,11(4):357-362.(LI Zhi-qiang,CHEN Shu-xun,WEI Qi -feng.Study on decoupled engine mounting system[J].JournalofDynamicsandControl,2013,11(4):357-362.(in Chinese)) [3] 李志强,陈树勋,韦齐峰.汽车动力总成悬置系统振动解耦计算方法研究[J].计算力学学报,2014,31(2):187-191.(LI Zhi-qiang,CHEN Shu-xun,WEI Qi -feng.Study on calculating method of vibration decoupling for automotive powertrain mounting system[J].ChineseJournalofComputationalMechanic,2014,31(2):187-191.(in Chinese)) [4] 褚志刚,熊 敏,杨 洋,等.车内噪声时域传递路径分析[J].振动与冲击,2015,34(17):161-166.(CHU Zhi-gang,XIONG Min,YANG Yang,et al.Time -domain transfer path analysis of automobile interior noise[J].JournalofVibrationandShock,2015,34(17):161-166.(in Chinese)) [5] 兰凤崇,谢 然,陈吉清.车辆发动机悬置处的动态刚度仿真研究[J].振动、测试与诊断,2009,29(3):303-307.(LAN Feng-chong,XIE Ran,CHEN Ji-qing.Simulation study on dynamic stiffness of engine mounting points on car body[J].JournalofVibration,Measurement&Diagnosis,2009,29(3):303-307.(in Chinese)) [6] 赵旭光,姜 潮,于 盛.汽车发动机悬置系统的多目标优化[J].机械科学与技术,2015,34(12):1940-1946.(ZHAO Xu-guang,JIANG Chao,YU Sheng.Multi-objective optimization design of vehicle engine mounting system[J].MechanicalScienceandTechnologyforAerospaceEngineering,2015,34(12):1940-1946.(in Chinese)) [7] 谢 展,于德介,李 蓉,等.基于区间分析的发动机悬置系统稳健优化设计[J].汽车工程,2014,36(12):1503-1507,1527.(XIE Zhan,YU De -jie,LI Rong,et al.Robust optimization design of engine mount systems based on interval analysis[J].AutomotiveEngineering,2014,36(12):1503-1507,1527.(in Chinese)) [8] 余 烽,徐中明.基于模拟退火算法的全地形车发动机悬置系统参数优化[J].四川兵工学报,2013,34(9):60-63.(YU Feng,XU Zhong-ming.The parameter optimization of ATV’s engine mounting system based on simulated annealing algorithm [J].SichuanOrdnanceJournal,2013,34(9):60-63.(in Chinese)) [9] 张 武,陈 剑,高 煜.基于粒子群算法的发动机悬置系统稳健优化设计[J].农业机械学报,2010,41(5):30-35.(ZHANG Wu,CHEN Jian,GAO Yu.Robust optimal design of an engine mounting system based on particle swarm optimization[J].TransactionsoftheChineseSocietyforAgriculturalMachinery,2010,41(5):30-35.(in Chinese)) [10] 庄伟超,王良模,殷召平,等.基于遗传算法的混合动力汽车动力总成悬置系统的优化设计研究[J].振动与冲击,2015,34(8):209-213.(ZHUANG Wei-chao,WANG Liang-mo,YIN Zhao -ping,et al.Optimization design for powertrain mounting system of a hybrid electric vehicle via genetic algorithm[J].JournalofVibrationandShock,2015,34(8):209-213.(in Chinese)) [11] 张俊红,王凯楠,毕凤荣,等.基于状态空间的车辆耦合振动系统分析及优化[J].中国机械工程,2014,25(21):2975-2981.(ZHANG Jun-hong,WANG Kai-nan,BI Feng-rong,et al.Analysis and optimization of coupled vibration system for vehicle based on state space[J].ChinaMechanicalEngineering,2014,25(21):2975-2981.(in Chinese)) [12] 胡 倩,陈 剑,沈忠亮,等.计及隔振率的发动机悬置系统稳健优化设计[J].噪声与振动控制,2015,35(4):78-84.(HU Qian,CHEN Jian,SHEN Zhong-liang,et al.Robust optimal design of an engine mounting system considering isolation rate[J].NoiseandVibrationControl,2015,35(4):78-84.(in Chinese)) [13] Löfdahl M,Johnsson R,Nykänen A.Mobility mea-surement in six DOFs applied to the hub of a car [J].AppliedAcoustics,2014,83:108-115. [14] Wu Y,Yu K P,Jiao J,et al.Dynamic modeling and robust nonlinear control of a six-DOF active micro -vibration isolation manipulator with parameter uncertainties[J].MechanismandMachineTheory,2015,92:407-435. [15] Zhan J M,Cai W H,Hu W Q,et al.Numerical study on the six-DOF anchoring process of gravity anchor using a new mesh update strategy[J].MarineStructures,2017,52:173-187.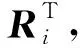





6 结 论
