基于浸入边界-格子Boltzmann通量求解法的椭圆柱流动特性分析

， ，

(哈尔滨工业大学 能源科学与工程学院,哈尔滨 150001)

1 引 言

钝体绕流现象是流体力学的经典问题之一，国内外学者[1-4]对单圆柱、串并列双圆柱及多个圆柱的绕流进行了深入研究，较好地揭示了其尾迹与受力特性的演化规律和机制。在实际工程中，除了圆形截面外，具有椭圆形或矩形截面特征的柱体结构也广泛应用于电力冷却系统、换热器和流体机械等领域。其中，椭圆形柱体具有流动阻力低、换热效果好的优点，越来越受到人们的重视，因此开展椭圆柱绕流研究具有重要的实际意义。Dennis等[5]分析了低雷诺数条件下攻角对单椭圆柱流场结构及升阻力特性的影响规律；Justin等[6]研究了单椭圆柱绕流尾迹模态随长短轴比值的变化情况；Peng等[7]开展了几何参数及并列椭圆柱间距对流场尾迹旋涡特性的研究；梁才航等[8]针对椭圆柱流动状态及传热特性开展了相应的研究工作。上述数值研究均是基于单个及并列椭圆柱绕流问题展开的，然而在海洋石油平台支柱和冷凝器排管等实际应用中存在串列的布置形式，因此有必要开展串列椭圆柱绕流的研究工作。

近20多年来，格子Boltzmann方法(Lattice Boltzmann Method)在理论方面取得了很大的进展[9,10]，现已拓展到可圧缩流体、多相流体和燃烧学等应用领域[11-13]，成为计算流体动力学的重要数值方法。与传统求解宏观方程不同，LBM是介于流体的微观分子动力学模型和宏观连续模型之间的介观模型，主要研究假象粒子的动力学，具有演化过程清晰、边界处理容易和压力求解简单等优点[14]。然而，该方法尚存在一些缺点,由于格子速度模型的引用，LBM的求解局限于均匀直角网格，时间推进步长与网格尺度存在相关性，导致计算较高雷诺数流动问题时，必须采用较密的网格来保证计算程序的稳定性，进而大幅降低了其计算效率。

本文对雷诺数为100的单椭圆柱及串列双椭圆柱进行了数值研究，着重分析了单椭圆柱升阻力系数和斯特劳哈尔数随长短轴比值的变化规律以及串列双椭圆柱升阻力和流动形态随间距的变化规律。采用Shu等[15]提出的格子Boltzmann通量求解方法(Lattice Boltzmann Flux Solver)，基于有限体积思想，状态变量由宏观方程给出，界面通量用格子玻尔兹曼的介观模型构造，克服了传统格子玻尔兹曼方法只能在均匀网格下求解的缺点，并改善了传统流体动力学计算方法必须花费大量时间求解泊松方程而受到压力场的限制，大大节约了数值计算的时间。此外，采用文献[16,17]提出的强制浸入边界法处理椭圆柱物面边界，以精确满足无滑移条件。

2 数值方法

本文采用宏观不可压N-S控制方程表达式为

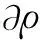
(1)

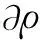
(2)

在低速流动条件下,基于多尺度Chapman-Enskog展开建立格子波尔兹曼方程中密度分布函数与宏观方程状态变量及通量之间的关系，采用浸没边界-格子波尔兹曼通量求解(Immersed Boun-dary-lattice Boltzmann Flux Solver) 的不可压控制方程表达式为

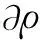
(3)

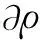
(4)

(5)

fneqα=-τδt(∂/∂t+eα·)feqα

(6)

针对以上控制方程，空间离散形式为

(7)

在计算域节点处理方面，IB -LBFS方法中包括代表流场区域的欧拉点和代表物理边界的拉格朗日点，如图1所示，其本质是将浸入边界模化成流场中的力源项，从而使整个流场的计算可以使用简单的笛卡尔网格,而不用按照物体表面的形状生成复杂的贴体网格，简化了网格生成过程。

计算过程主要分为两个部分。

(1) 不考虑边界作用力,使用界面通量重构(LBFS)求解控制方程:

(8)

(9)

(2) 采用强制浸入边界法(IBM)修正宏观变量，进而求得边界作用力：

(10)

求解控制方程的关键是求解两个单元界面上的通量，本文基于格子波尔兹曼模型在网格界面处重构数值格式(LBFS)，如图2所示，通量表示为

(11)

(12)

通过泰勒级数展开，非平衡项可以用平衡项表示为

fneqα(r,t)=-τ[feqα(r,t)-feqα(r-eαδt-ri,t)]

(13)

因此只要求得平衡项feqα(r-eαδt-ri,t)与feqα(r,t)便可求得界面通量。

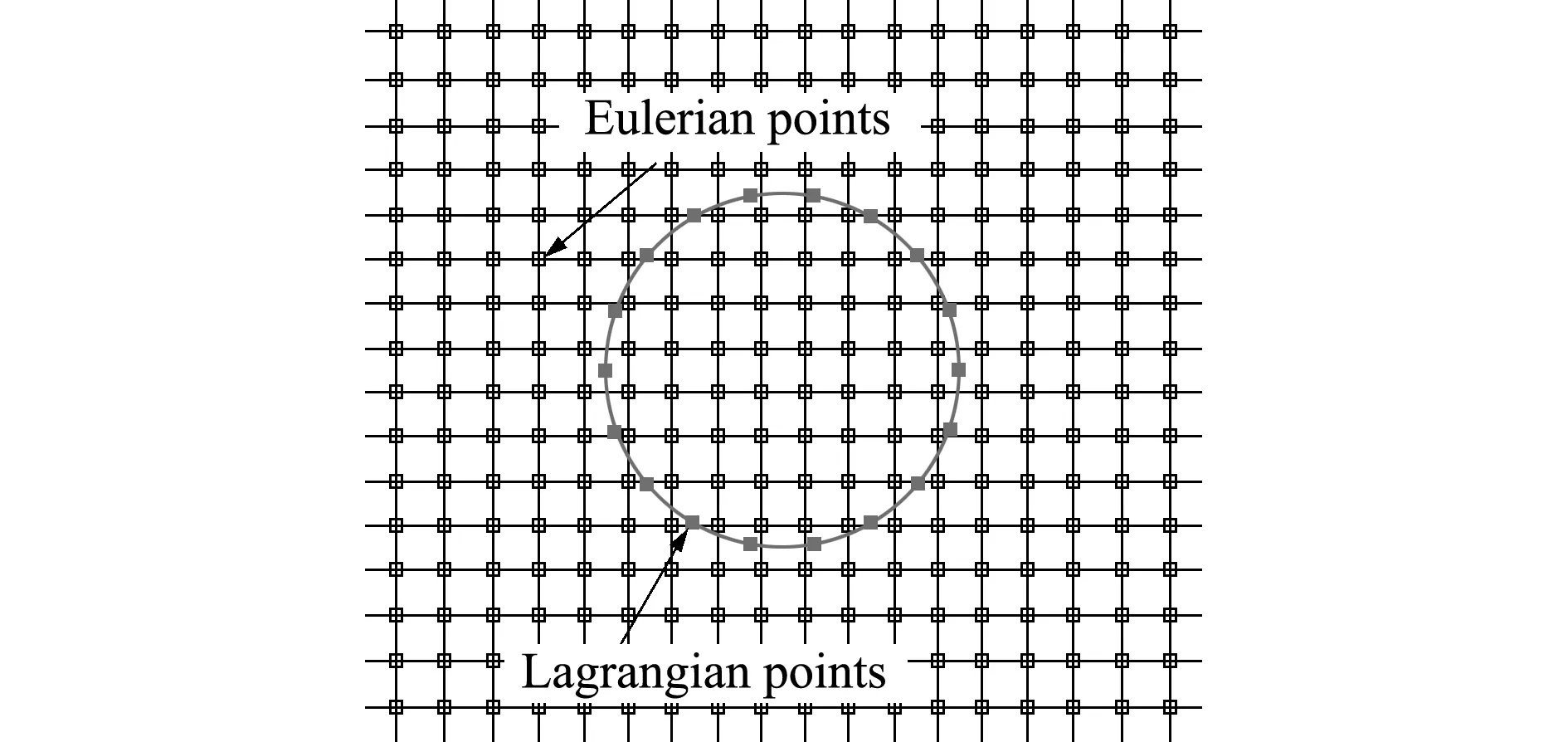
图1 计算域二维示意图

Fig.1 A solid boundary immersed in a two -dimensionalcomputational domain

图2 界面通量重构示意图

Fig.2 Local flux reconstruction at cell interface

已知相邻两个网格单元和界面的物理位置，分别定义为ri,ri +1和r，则有

(14)

基于以上方法，可以得到重构后界面宏观变量密度和动量的表达式为

(15)

(16)

再通过LBGK模型求得feqα(r,t)。

在壁面处理方面，应用强制浸入边界法进行流场速度的修正，使得物面满足无滑移边界条件。

定义u*为流场瞬时速度，修正后的欧拉点速度表达式为

un +1=u*+Δu

(17)

欧拉点上修正速度可以通过Dirac delta 函数插值求解，表达式为

(l=1,…,N) (18)

式中D为连续kernel函数，表达式为

(19)

(20)

为了保证无滑移边界条件，边界上拉格朗日点的速度等于同一位置流场的速度，则需要通过插值来求解拉格朗日点的流动速度，

(21)

式中l=1,…,N;j=1,…,M;h为欧拉点网格尺寸，N和M分别为拉格朗日点与欧拉点的个数，拉格朗日点上的速度为

(22)

将式(22)写成矩阵的形式为

AX=B

(23)

(24)

(25)

(26)

3 数值验证

(27)

(28)

St=f·D/U∞

(29)

式中Fd和Fl分别为浸入边界所受到的阻力和升力，fx和fy为边界点上沿水平和竖直方向上的分力，f为旋涡脱落的无量纲频率。

由表1数值计算结果与其他文献结果对比可知，本文计算得到的圆柱绕流升阻力系数与斯特劳哈尔数均与文献结果吻合良好，充分说明了IB -LBFS求解低雷诺数不可压流动绕流问题的精确性。

4 单椭圆柱绕流问题

单椭圆柱绕流的计算域及边界条件如图3所示，雷诺数Re=100，无量纲长度D=Dy=1.0，定义椭圆柱长短轴径的比值(aspect ratio)为AR=Dx/Dy，保持短轴尺寸不变，通过改变长轴尺寸研究AR=1.0,1.25,1.5,1.75,2.0,2.5,3.0和5.0八种情况下的椭圆柱绕流与受力特性。

从图4(b)可以看出，最大升力系数随AR值的增大而减小，当AR≥3.0时，升力系数为0，而进一步研究长短轴比值及串列双椭圆柱间距对流动和受力的影响规律。图6为串列双椭圆柱计算域示意图，边界条件与单椭圆柱绕流的边界条件相同；雷诺数Re=100，无量纲长度D=Dy=1.0；分别模拟了AR=1.0，1.5，2.0以及L/D=1.0，2.0，3.0，4.0，5.0，7.0，9.0不同间距的流场，其中L代表串列椭圆柱之间的距离。

表1 非定常圆柱绕流升阻力系数与斯特劳哈尔数

Tab.1 Drag and lift coefficients，and Strouhal number for unsteady flow past a circular cylinder

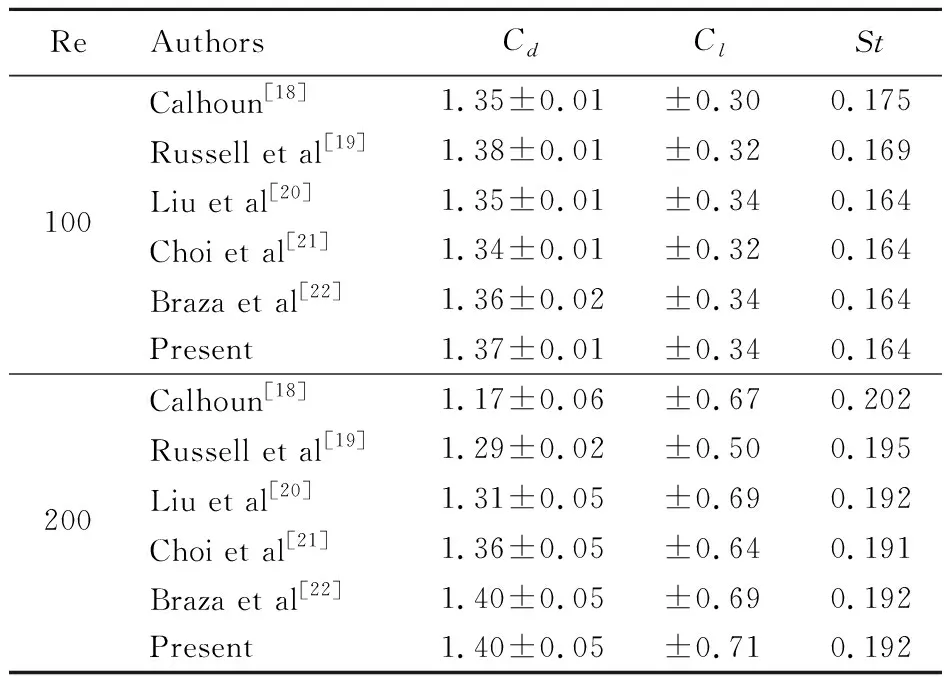
ReAuthorsCdClStCalhoun[18]1.35±0.01±0.300.175Russell et al[19]1.38±0.01±0.320.169100Liu et al[20]1.35±0.01±0.340.164Choi et al[21]1.34±0.01±0.320.164Braza et al[22]1.36±0.02±0.340.164Present1.37±0.01±0.340.164Calhoun[18]1.17±0.06±0.670.202Russell et al[19]1.29±0.02±0.500.195200Liu et al[20]1.31±0.05±0.690.192Choi et al[21]1.36±0.05±0.640.191Braza et al[22]1.40±0.05±0.690.192Present1.40±0.05±0.710.192

图3 椭圆柱绕流计算域

Fig.3 Computational domain of 2D elliptical cylinder

表2表明，斯特劳哈尔数也随AR值的增大而减小，当AR≥3.0时，没有检测到周期性的尾缘脱落现象，这说明此时椭圆柱绕流为稳定流动。

图5表明随着AR的增加，椭圆柱绕流时均分离涡与来流垂直方向的尺寸变小，这也说明了其分离角度的减小，而分离涡的长度则先增加后减小。

表2 斯特劳哈尔数及分离角度随AR的变化规律

Tab.2 Strouhal number and separation angle with increasing aspect ratios

图4 平均阻力系数及最大升力系数随AR的变化规律

Fig.4 Variation in drag coefficient and maximum lift coefficient withAR

图5 不同AR下椭圆柱绕流时均流线图

Fig.5 Time -averaged streamlines with different aspect ratio

5 串列双椭圆柱绕流问题

图7给出了串联双椭圆系统中，上下游椭圆柱平均阻力系数随间距的变化规律。串列圆柱阻力系数与文献[23,24]的数值对比再次验证了本文数值方法的可靠性，表明IB -LBFS能很好地捕捉层流绕流特性。从上下游椭圆柱的阻力系数对比可知，在相同AR及L/D的条件下，上游椭圆柱的阻力大于下游椭圆柱阻力，且AR越大，上游椭圆柱阻力系数越小。

图7(a)表明，在相同的间距下，上游椭圆柱的阻力系数随AR的增加而减小，这与单个椭圆柱阻力的变化规律相同。在较小的间距下，上游椭圆柱阻力随着间距的增加呈现小幅度降低的趋势，这是由于间距的增加使得上游椭圆柱分离的剪切层有较大的空间发展，分离点后移，引起阻力的降低。随着间距的继续增加，存在一临界间距，出现阻力跃升现象，当AR=1.0时，该临界值为L/D=2.0～3.0；当AR=1.5和2.0时，临界值基本相同，出现在L/D=3.0～4.0之间，此时上游椭圆柱尾迹区形成脱落涡。当间距大于临界间距时，椭圆柱阻力变化规律与圆柱有所不同。对于圆柱，阻力随间距的变大先变小再变大，逐渐趋于单个圆柱绕流的阻力，这与现有文献结论相符；对于椭圆柱，阻力随间距的变大基本保持不变，再小幅增加，逐渐趋于相同AR值下单个椭圆柱绕流的阻力系数，说明此时下游椭圆柱对上游椭圆柱受力影响较小。

图6 串列双椭圆柱绕流计算域

Fig.6 Computational domain of two tandem elliptic cylinders

图7(b)表明，在较小的间距下(L/D≤2.0)，AR值越大，下游椭圆柱阻力系数越大，且AR=1.0 时的阻力系数为负值，即下游圆柱受到了指向上游的吸力；AR=1.5或2.0时的阻力为正值。当间距达到临界间距时，下游椭圆柱也出现了阻力跃升。随着间距进一步增加到L/D=7.0时，下游椭圆柱阻力随间距的变化规律略有不同，这是由于不同的间距导致上游椭圆柱的非定常脱落涡结构作用在下游椭圆柱上，使得下游椭圆柱的附着点与分离点位置发生变化，造成椭圆柱前后压差以及壁面摩擦力的波动所致。当L/D≥7.0时，阻力系数随着间距的增加而缓慢增加，且AR值越大，阻力系数越大。

为了研究流动形态的变化，图8给出了AR=1.0，1.5及2.0情况下，斯特劳哈尔数随双椭圆柱间距的变化规律以及不同间距下的瞬时涡量图。

从图8可以看出，当AR=1.0时，较小间距下St值随着间距的增加有小幅下降；结合涡量云图9可以看出，L/D=1.0和2.0时，上游圆柱剪切层没有足够的空间发展为脱落涡结构而附着在下游圆柱表面上，在下游圆柱后方形成周期性漩涡脱落状态，间距的变大使得涡长度增加，因此脱落涡频率降低；当达到临界间距时，St突然增大，表明此时上游圆柱尾迹区域开始形成脱落涡结构；当L/D≥3.0时，St随间距的增加逐渐趋近于单个圆柱绕流的St值，上游圆柱产生的涡脱涡交替或间歇作用于下游圆柱上，并从下游圆柱表面脱落。由于串列圆柱直径相同，因此两圆柱的脱落涡频率相同。

图7 椭圆柱阻力系数随间距的变化规律

Fig.7 Dependence of the mean drag coefficient of onthe dimensionless spacingL/D

当AR=1.5和2.0时，在间距1.0≤L/D≤3.0 范围内，流动呈现稳定流动状态，如图10和 图11 所示，在上下游椭圆柱尾迹区均无脱落涡形成，St值为0，说明此时下游椭圆柱可以有效抑制上游椭圆柱流动分离的现象；当间距达到临界间距，即L/D=3.0～4.0时，上游椭圆柱尾迹区域形成的脱落涡结构作用在下游椭圆柱表面，在下游椭圆柱尾迹区域形成同样频率的脱落涡结构，导致St突然增大；随着间距的继续增加，St值逐渐趋于单个椭圆柱绕流的St值。此外，图10和图11进一步表明了串列椭圆柱的临界间距大于串列圆柱。

图8 斯特劳哈尔数随间距的变化规律

Fig.8 Dependence of the Strouhal number on the dimensionless spacingL/D

图9AR=1.0时不同间距瞬态涡量图

Fig.9 Instantaneous vorticity atAR=1.0

图10AR=1.5时不同间距瞬态涡量图

Fig.10 Instantaneous vorticity atAR=1.5

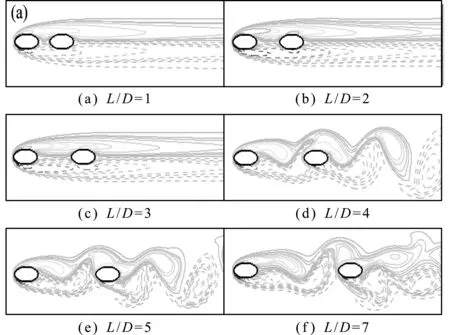
图11AR=2.0时不同间距瞬态涡量图

Fig.11 Instantaneous vorticity atAR=2.0

6 结 论

本文应用浸入边界-格子玻尔兹曼通量求解法对椭圆柱绕流开展了数值研究。首先通过单圆柱非定常计算验证了数值方法的可靠性，进而模拟了低马赫数下Re=100时单椭圆及串列双椭圆柱绕流流动，分析了长短轴比值和间距几何参数对其流场及受力特性的影响规律，结论如下。

(1) 对于单椭圆柱，平均阻力系数先随长短轴比值AR的增加而降低，而后呈现缓慢上升趋势；升力系数最大值随长短轴比值的增大而减小；压差阻力与摩擦阻力呈相反的变化规律，当AR<2.5时，压差阻力起主导作用，而随着AR值的增加，摩擦阻力起主导作用。随着AR值的增加，绕流体后方由周期性的旋涡脱落状态转变为稳定对称流动。

(2) 对于串列双椭圆柱，上下游椭圆柱阻力随间距的变化规律与串列圆柱基本相同,但其临界间距不同。在较小的间距下，上游椭圆柱阻力随间距的增加而降低，而下游椭圆柱的阻力随间距的变大而变大；当间距增大到临界间距时，上下游椭圆柱阻力均跃升，且串列椭圆柱临界间距大于串列圆柱，而后随间距的变大阻力有所波动；当L/D≥7.0时，上下游椭圆柱阻力随间距增加而增加，逐渐趋近于此长短轴比值下的单椭圆柱阻力。

(3) 在较小的间距下，串列圆柱呈现周期性脱落形式，而串列双椭圆柱流动状态则为稳定流动，即下游椭圆柱可以有效地抑制上游椭圆柱流动分离的现象；随着间距的增加，串列双椭圆柱与串列圆柱流动状态一致，在上下游椭圆柱及圆柱后方均呈现周期性的脱落涡，不断增加的间距对流动状态的影响越来越小，上下游钝体绕流形式均趋于相同长短轴比值下的单钝体绕流。

:

[1] Harichandan A B,Roy A.Numerical investigation of low Reynolds number flow past two and three circular cylinders using unstructured grid CFR scheme[J].InternationalJournalofHeatandFluidFlow,2010,31(2):154-171.

[2] Patil D V,Lakshmisha K N.Two -dimensional flow past circular cylinders using finite volume lattice Boltzmann formulation[J].InternationalJournalforNumericalMethodsinFluids,2011,69(6):1149-1164.

[3] Ding H,Shu C,Yeo K S,et al.Numerical simulation of flows around two circular cylinders by mesh-free least square-based finite difference methods[J].InternationalJournalforNumericalMethodsinFluids,2006,53(2):305-332.

[4] 张忠宇,姚熊亮,张阿漫.基于间断有限元方法的并列圆柱层流流动特性[J].物理学报,2016,65(8):236-247.(ZHANG Zhong-yu,YAO Xiong-liang,ZHANG A-man.Numerical simulation of laminar flow past two side -by-side cylinders by discontinuous Galerkin method[J].ActaPhysicaSinica,2016,65(8):236-247.(in Chinese))

[5] Dennis S C R,Young P J S.Steady flow past an elliptic cylinder inclined to the stream[J].JournalofEngineeringMathematics,2003,47(2):101-120.

[6] Leontini J S,Jacono D L,Thompson M C.Stability analysis of the elliptic cylinder wake[J].JournalofFluidMe-chanics,2015,763:302-321.

[7] Peng Y F,Sau A,Hwang R R,et al.Criticality of flow transition behind two side-by-side elliptic cylinders[J].PhysicsofFluids,2012,24(3):034102.

[8] 梁才航,杨永旺,黄斯珉.绕椭圆柱管束的流动与传热特性[J].科学技术与工程.2013,13(13):3592-3597.(LIANG Cai-hang,YANG Yong-wang,HUANG Si-min.Fluid flow and heat transfer across an elliptical cylinder tube bank[J].ScienceTechnologyandEngineering,2013,13(13):3592-3597.(in Chinese))

[9] 郭照立，郑楚光.格子Boltzmann方法的原理与应用[M].北京：科学出版社，2009.(GUO Zhao -li,ZHENG Chu-guang.TheoryandApplicationsofLatticeBoltzmannMethod[M].Beijing:Science Press,2009.(in Chinese))

[10] 何雅玲，王 勇，李 庆.格子Boltzmann方法的理论及应用[M].北京：科学出版社，2009.(HE Ya-ling,WANG Yong,LI Qing.LatticeBoltzmannMethod:TheoryandApplications[M].Beijing:Science Press,2009.(in Chinese))

[11] Lin C,Xu A,Zhang G,et al.Polar-coordinate lattice Boltzmann modeling of compressible flow[J].PhysicalReviewE,2014,89(1):013307.

[12] Xu A,Lin C,Zhang G,et al.Multiple -relaxation-time lattice Boltzmann kinetic model for combustion[J].PhysicalReviewE,2015,91(4):043306.

[13] Lai H L,Xu A G,Zhang G C,et al.Nonequilibrium thermohydrodynamic effects on the Rayleigh-Taylor instability in compressible flows[J].PhysicalReviewE,2016,94(2):023106.

[14] 聂德明,郑梦娇,高 原,等.并列双椭圆柱绕流的格子Boltzmann虚拟区域方法的模拟研究[J].计算力学学报,2014,31(4):517-525.(NIE De -ming,ZHENG Meng-jiao,GAO Yuan,et al.Numerical investigation of flow past two elliptical cylinders in side by side arrangement via lattice Boltzmann-fictitious domain method[J].ChineseJournalofComputationalMe-chanics,2014,31(4):517-525.(in Chinese))

[15] Shu C,Wang Y,Teo C J,et al.Development of Lattice Boltzmann flux solver for simulation of incompressible flows[J].AdvancesinAppliedMathematicsandMechanics,2014,6(4):436-460.

[16] Wang Y,Shu C,Teo C J,et al.An immersed boundary-lattice Boltzmann flux solver and its applications to fluid-structure interaction problems[J].JournalofFluidsandStructures,2015,54:440-465.

[17] Wang Y,Shu C.Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications[J].JournalofComputationalPhysics,2009,228(6):1963-1979.

[18] Calhoun D.A Cartesian grid method for solving the two -dimensional streamfunction-vorticity equations in irregular regions[J].JournalofComputationalPhysics,2002,176(2):231-275.

[19] Russell D,Wang Z J.A Cartesian grid method for modeling multiple moving objects in 2D incompressible viscous flow[J].JournalofComputationalPhysics,2003,191(1):177-205.

[20] Liu C,Zheng X,Sung C H.Preconditioned multigrid methods for unsteady incompressible flows[J].JournalofComputationalPhysics,1998,139(1):35-57.

[21] Choi J I,Oberoi R C,Edwards J R,et al.An immersed boundary method for complex incompressible flows[J].JournalofComputationalPhysics,2007,224(2):757-784.

[22] Braza M,Chassaing P,Minh H H.Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder[J].JournalofFluidMechanics,1986,165(1):79-130.

[23] Mussa A,Asinari P,Luo L S.Lattice Boltzmann simulations of 2D laminar flows past two tandem cylinders[J].JournalofComputationalPhysics,2009,228(4):983-999.

[24] Sharman B,Lien F S,Davidson L,et al.Numerical predictions of low Reynolds number flows over two tandem circular cylinders[J].InternationalJournalforNumericalMethodsinFluids,2005,47(5):423-447.