配置点谱方法-人工压缩法(SCM-ACM)求解不可压缩流体流动

， ， ， ，

1 引 言

人工压缩法是Chorin提出来的，通过改变方程的类型来求解不可压缩黏性流体流动，具有形式简单、准确有效且易于实施的特点。求解不可压缩流动问题的关键是解决速度场与压力场的耦合问题。应用原始变量方程求解非定常不可压缩N-S方程，已有多种解决速度场与压力场之间耦合的办法。作为求解原始变量方程之一的人工压缩法的基本思路是,通过在定常不可压缩黏性流动N-S方程组中添加一项时间导数项∂/∂t,将其转化为一种虚拟的非定常可压缩黏性流动N-S方程组，如果t→∞时，能保证∂/∂t→0,则非定常可压缩黏性流动逼近定常不可压缩黏性流动。在研究工作[7-11]中，ACM已应用于求解不可压缩和弱可压缩流动问题，并展示了ACM形式简单、准确有效及易于实施的特点。

目前，在求解不可压缩流动问题方面，离散控制方程常用的数值方法有有限差分法、有限体积法、有限元方法和谱方法等[12,13]，处理速度与压力耦合问题常用的方法有SIMPLE系列算法、涡量-流函数法、求解压力泊松方程方法和人工压缩法等。目前还没有发现将谱方法与人工压缩法进行结合用于求解不可压缩流动问题的相关文献。因此，本文结合两种方法的特点，开发了SCM-ACM用于求解不可压缩流动问题，并研究了SCM-ACM求解二维不可压缩流动问题的收敛特性，为不压缩流动问题的数值求解提供了新的选择。

2 人工可压缩格式的控制方程

本文选取流动问题的典型算例——二维方腔内的顶盖驱动流为计算对象。方腔顶盖驱动流(简称方腔流)是一个非常经典的流体力学问题，对其研究也非常广泛。尽管区域比较简单，但其包含了很复杂的流体流动特性，如主涡、次级涡、剪切流及边界层等。同时，方腔流也是验证新数值方法的经典算例。

下面给出了求解顶盖驱动流所涉及到的不可压缩格式的非稳态控制方程。

(1)

(2)

(3)

式中 人工压缩法中的参数c为可压缩粘性流动声速，Re为雷诺数，U和V分别为x和y方向上的无量纲速度，P为无量纲压力。

方腔内为粘性不可压缩流体，满足如下无滑移边界条件，

y=1处：U=1,V=0;

x=0,1,y=0处：U]0,V=0。

3 数值方法

本文采用配置点谱方法离散空间偏导数，其具体离散过程包括计算区域的转换和系数的确定。

3.1.1 计算区域的转换

采用谱方法进行求解，必须要求所求解变量在[0,1]之间的规则区域内，因此计算区域转换是必要的步骤，在直角坐标系内，二维问题的区域转换如下。

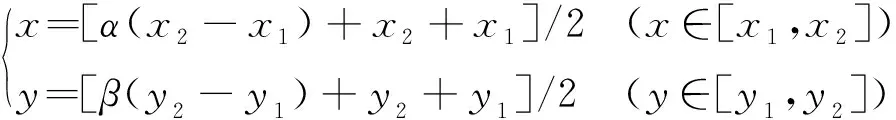
(4)

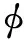
(5)

(6)

3.1.2 系数的确定

本文所采用的是一种直接的配置点谱方法，控制方程中的参数和系数用离散的系数矩阵代替。

假设，

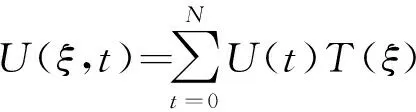
(7)

式中T(ξ)为Chebyshev多项式，ξ=cos(πj/N),j=0,1，…，N，相应的变量u(ξ,t)对ξ的一阶导数用Chebyshev多项式离散的表达式为

(8)

式中

写成矩阵形式为

其中一阶导数矩阵系数(DN)i j为

(9)

(10)

由式(10)得出其一阶导数和二阶导数的形式分别为

(11)

(12)

式中d(2)i,j的表达式可由d(2)i,j=d(1)i,jd(1)i,j得出。

针对离散后的矩阵形式的代数方程采用隐格式求解方法进行求解，其中对流项采用显式的Adams-Bashforth格式，扩散项和压力项采用隐式格式，具体离散形式如下。

(13)

(14)

(15)

式中 Δt为时间步长，本文取Δt=10-5,U为速度矢量。对离散后矩阵形式的N-S采用二步直接求解法[14]即可直接求解出速度分布。

4 结果分析

选取方腔内的平均流函数作为网格独立性测试的敏感变量，并在横纵坐标方向选取相同数目的网格节点(10～70)，雷诺数为100时，平均流函数随网格节点的变化如图1所示。

可以看出，网格节点数较少时(10～30)，平均流函数值变化较大；当网格节点数超过30时，平均流函数值变化微小，所以对网格独立性检验的精度影响程度很小。除此之外，不同的网格节点数对应的计算时间也有较大差别，网格节点数到70时所用的计算时间较长，约为网格节点数为40时的 4倍，表1给出了不同节点数对应的计算时间。因此，综合考虑计算时间和精度，本文选取网格节点数为40。

由于缺少实验结果，选取数值计算结果对SCM-ACM求解二维方腔内顶盖驱动流问题进行代码有效性验证。本文分别对Re=100和 Re=1000时，方腔内的流场分布和速度分布进行了比较和验证。

表1 不同网格节点数(10～70)对应的计算时间

Tab.1 Calculation time corresponding to the number of grid nodes (10～70)

节点数目10203040506070计算时间/s1350240032004800120001300020000

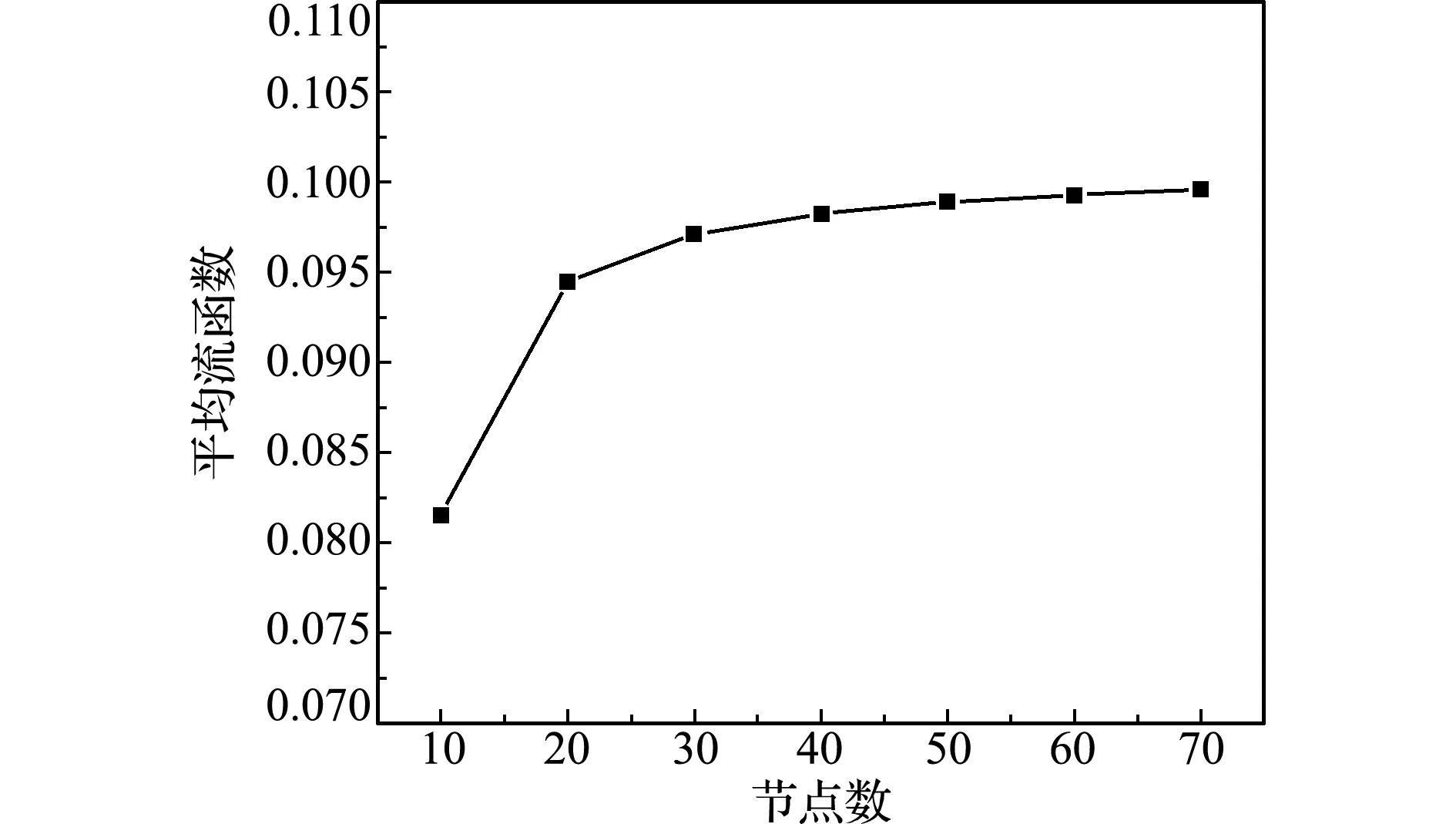
图1 Re=100时平均流函数随网格节点数的变化

Fig.1 Change of average stream function with the number of grid nodes with Re=100

图2给出了Re=100时本文的计算结果和参考文献结果的比较。可以看出，本文的计算结果与Li等[14]的计算结果吻合较好，而与Rahman等[15]的结果则有轻微差异。与图2(a，b)相比，Rahman等[15](图2(c))计算的流场中心漩涡偏右上。为了更细致地检验结果的准确性，图3给出了方腔中线x=0.5处速度U沿y方向的分布。流场分布(图2)能从宏观上检验流动分布的有效性，而速度U的分布则能更细致地检验本文计算结果的准确性。从中线x=0.5处速度U的分布可以看出，本文的计算结果与参考文献的结果几乎重合，说明本文的计算结果具有很好的准确度。

为了更好地检验SCM-ACM代码的有效性，本文给出了Re=1000时流场分布和速度分布的验证，分别如图4和图5所示。在流场宏观分布为了检测SCM-ACM的收敛特性，本文给出了收敛误差随迭代次数的变化趋势。收敛误差定义为后一时层所有节点速度值(或压力)与前一时层所有节点速度值(或压力)的最大差值，如速度U的误差为ε(U)=max(Un+1-Un)。

图2 Re=100时方腔内流场分布

Fig.2 Flow field distribution in a square cavity with Re=100上，Re=1000时本文的计算结果(图4(a))与参考文献[16,17]的结果吻合很好。中线x=0.5处速度U的分布结果显示，本文的计算结果与Erturk等[18]以及Li等[14]的结果几乎重合，说明在Re=1000时，本文开发的SCM-ACM仍具有很好的计算精确度。

图3 Re=100时速度U在x=0.5中心线处的分布

Fig.3 Distribution ofUatx=0.5 with Re=100

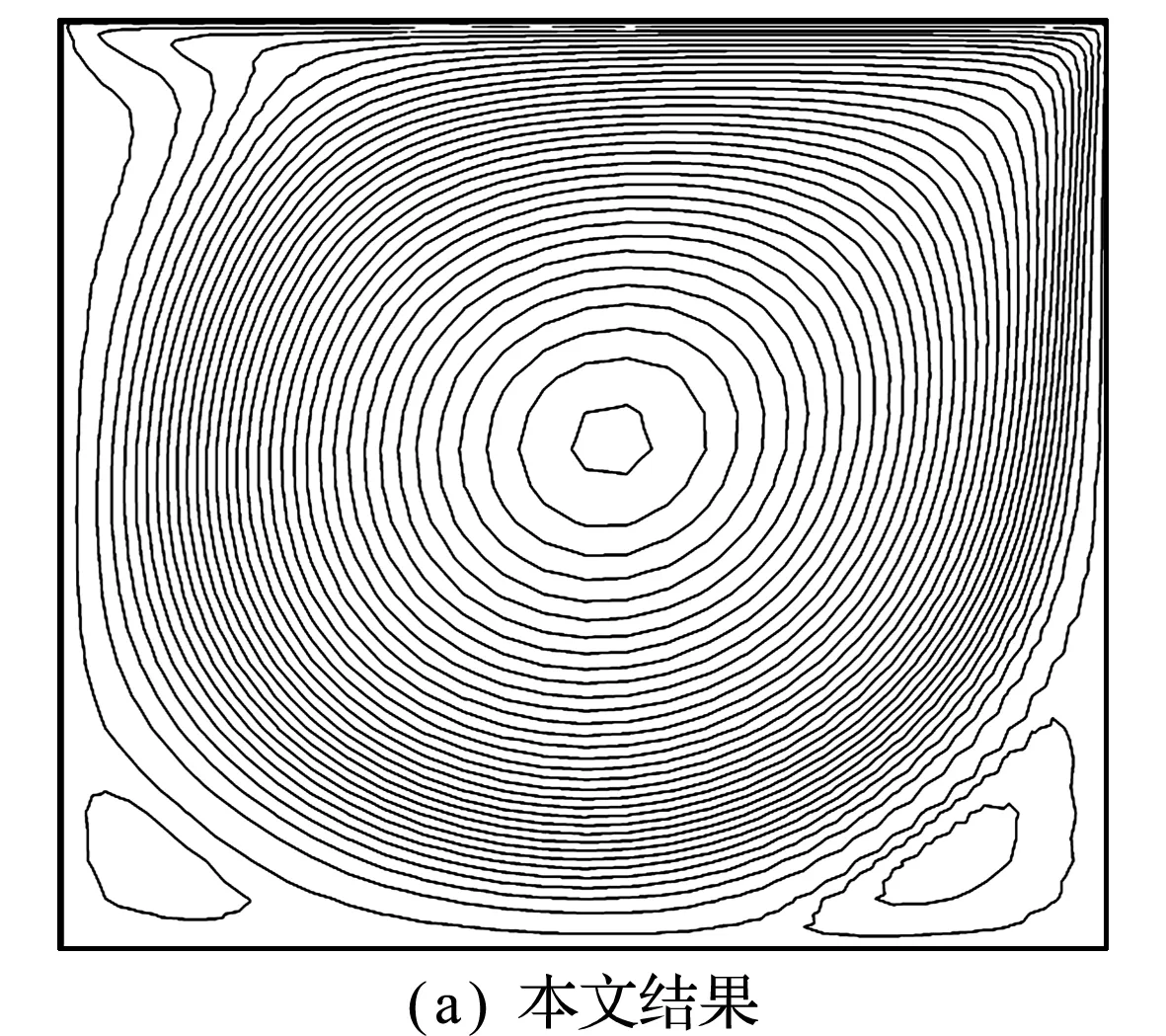
图4 Re=1000时方腔内流场分布

Fig.4 Flow field distribution in a square cavity with Re=1000

图6给出了Re=100和1000时，速度分量U，V和压力P的收敛误差随迭代次数的变化，其中纵坐标为对数坐标。可以看出，速度和压力的误差随迭代次数的增加呈指数下降(迭代初期除外)，这种收敛特性继承自谱方法。在迭代初期误差的快速变化是由U，V和P给定的初值所引起的。

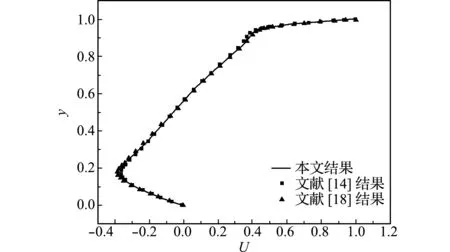
图5 Re=1000时速度U在x=0.5中心线处的分布

Fig.5 Distribution ofUatx=0.5 with Re=1000

图6 速度分量U，V和压力P的误差随迭代次数的变化

Fig.6 Errors of the velocity componentU，Vand pressurePagainst calculation steps with Re=100 and Re=1000

5 结 论

基于SCM和ACM各自的优点，本文开发了SCM-ACM数值方法，并选用经典的顶盖驱动流为测试对象，检验了SCM-ACM求解不可压缩流动问题的网格独立性和代码有效性，分析了SCM-ACM的收敛特点。研究结果显示，本文开发的SCM-ACM能够有效地用于求解不可压缩流动问题，并具有指数收敛的特点，为不可压缩粘性流动问题的求解提供了一种新的选择。

:

[1] Benwen L I，Zhang W.Direct solvers for discrete ordinates equations based on Chebyshev collocation spectral method[J].JournaloftheChemicalIndustry&EngineeringSocietyofChina，2010，61(2):296-301.

[2] Shen J，Yang X F.An efficient moving mesh spectral method for the phase -field model of two -phase flows[J].JournalofComputationalPhyscis，2009，228(8):2978-2992.

[3] Chen Y Y，Li B W，Zhang J K.Spectral collocation method for natural convection in a square porous cavity with local thermal equilibrium and non-equilibrium models[J].InternationalJournalofHeatandMassTransfer，2016，96:84-96.

[4] Sun Y S，Ma J，Li B W.Spectral collocation method for convective-radiative transfer of a moving rod with variable thermal conductivity[J].InternationalJournalofThermalSciences，2015，90:187-196.

[5] Zhang C M,Song X T,Treeviriyanupab P，et al.Delayed error verification in quantum key distribution[J].ChineseScienceBulletin，2014，59(23):2825-2828.

[6] 李明昌，梁书秀，孙昭晨.异常天气条件下潮位过程神经网络补遗预测方法的研究[J].计算力学学报，2008，25(3):368-372.(LI Ming-chang，LIANG Shu-xiu，SUN Zhao-chen.Research on tide supplemental prediction using ANN methods under unusual weather[J].ChineseJournalofComputationalMechanics，2008，25(3):368-372.(in Chinese))

[7] 张廼龙，郭小明.多尺度模拟与计算研究进展[J].计算力学学报，2010，28(s1):1-5.(ZHANG Nai-long，GUO Xiao -ming.Review on multiscale modeling and computation[J].ChineseJournalofComputationalMechanics，2010，28(s1):1-5.(in Chinese))

[8] Tanno I，Morinishi K，Satofuka N,et al.Calculation by artificial compressibility method and virtual flux method on GPU[J].Computers&Fluids，2011，45(1):162-167.

[9] Asinari P，Ohwada T，Chiavazzo E，et al.Link-wise artificial compressibility method[J].JournalofComputationalPhyscis，2012，231(15):5109-5143.

[10] Silva G，Semiao V.First- and second-order forcing expansions in a lattice Boltzmann method reproducing isothermal hydrodynamics in artificial compressibility form[J].JournalofFluidMechanics，2012，698:282-303.

[11] Clausen J R.Entropically damped form of artificial compressibility for explicit simulation of incompressible flow[J].PhysicalReviewE，2013，87(1):013309.

[12] 章争荣，张湘伟.二维定常不可压缩粘性流动N-S方程的数值流形方法[J].计算力学学报，2010，27(3):415-421.(ZHANG Zheng-rong，ZHANG Xiang-wei.Numerical manifold method for steady incompressible viscous 2D flow Navier-Stokes equations[J].ChineseJournalofComputationalMechanics，2010，27(3):415-421.(in Chinese))

[13] 陈德祥，刘 帅，徐自力,等.非稳态流动的隐式最小二乘等几何方法[J].计算力学学报，2015，32(5):639-643.(CHEN De -xiang，LIU Shuai，XU Zi-li,et al.Implicit least squares isogeometric method for unsteady flow[J].ChineseJournalofComputationalMechanics，2015，32(5):639-643.(in Chinese))

[14] Li Z Q，Wood R.Accuracy analysis of an adaptive mesh refinement method using benchmarks of 2D steady incompressible lid-driven cavity flows and coarser meshes[J].JournalofComputationalandAppliedMathematics，2015，275:262-271.

[15] Rahman M M，Alim M A，Sarker M M A.Numerical study on the conjugate effect of joule heating and magnato -hydrodynamics mixed convection in an obstructed lid-driven square cavity[J].InternationalCommunicationsinHeatandMassTransfer，2010，37(5):524-534.

[16] 梅 欢.谱元方法求解不可压缩流体流动及流动线性稳定性分析[D].重庆大学，2012.(MEI Huan.Spectral Element Methods for Incompressible Fluid Flow and Linear Stability Analysis of Flow[D].Chongqing University，2012.(in Chinese))

[17] Ghia U，Ghia K N，Shin C T.High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J].JournalofComputationalPhyscis，1982，48(3):387-411.

[18] Erturk E，Corke T C，Gökçöl G.Numerical solutions of 2D steady incompressible driven cavity flow at high Reynolds numbers[J].InternationalJournalforNumericalMethodsinFluids，2005，48(7):747-774.