迭代最小二乘卫星定位算法
2018-07-05王奉帅刘聪锋
王奉帅,刘聪锋
(1.中国电子科技集团公司第五十四研究所,河北 石家庄050081;2.西安电子科技大学,陕西 西安710071)
0 引言
全球定位系统具有全天候、全球性、实时连续性和高精度等特点,因此受到了广泛的应用,例如飞机导航、导弹制导、地球变形监测、汽车防盗跟踪和手机定位等等。
传统的卫星导航定位解算采用的是最小二乘算法,对观测矩阵进行求逆来获取未知向量,其中求逆过程包含了大量复杂的乘除运算,增加了系统功耗。坐标旋转数字计算方法 (Coordinate Rotation Digital Computer,CORDIC)的应用越来越广泛,该算法能够减少硬件对时间和空间资源的需求。MR Mosavi等人结合伪距和载波相位,利用传统最小二乘确定接收机坐标,定位精度有所提升[1]。Yuheng He等人处理定位解算时,每次旋转选择合适的CORDIC角度,可以简化最小二乘运算[2]。N.Rahemi等人根据伪距方差对观测矩阵加权,再用最小二乘求解,可以提高定位精度[3]。李春华等人提出了一种基于互差中值理论的加权最小二乘算法,该算法的定位精度较最小二乘算法和直接解算方法的定位精度有较大提高,并能有效地减少问题卫星的影响[4]。徐飞采用了CORDIC算法对旋转矩阵中的三角函数计算,实现了硬件加速[5]。
本文给出了基于CORDIC算法实现近似正交三角(Orthogonal-Triangular,QR)分解[6-9]的迭代最小二乘算法(以下简称迭代最小二乘算法),利用该算法进行定位解算,没有损失定位精度,而且运行稳定可靠。
1 GPS定位原理
最小二乘算法是导航设备最常用到的定位解算算法,该算法根据4颗或更多卫星的伪距解算出接收机位置[10]。卫星观测伪距及星地几何距离如图1所示。

图1 卫星观测伪距及星地几何距离
接收机接收到卫星k的伪距ρ(k),具有下述表达式:
ρ(k)=r(k)+c(dt-dt(k))+T(k)+I(k)+ε(k),
k=1,2,...,n。
(1)
r(k)表示卫星k到接收机的几何距离:

(2)
式(1)中包含了4个未知数x,y,z和dt,其他参数均能通过先验信息获得。显然该方程是非线性的,对r(k)在(x0,y0,z0)处展开泰勒级数,舍弃二阶及更高阶项可以得到:
(3)
将式(1)在(x0,y0,z0,dt0)处展开泰勒级数,并舍弃二阶及更高阶项可以得到
Ax=b,
(4)
其中,
其中,
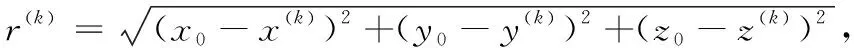
未知向量x是Ax=b的最小二乘解
minx‖Ax-b‖2。
(5)
可以得出x=(ATA)-1b,为了求出未知向量,需要对矩阵ATA求逆,这其中包含了复杂的运算,QR分解将矩阵ATA分解为Q和R矩阵,其中Q为正交矩阵,R为上三角矩阵。
2 基于CORDIC的近似QR分解算法
如果将式(4)左乘矩阵AT,可以得到
ΑTΑx=ΑTb;
(6)
若矩阵ATA能够进行QR分解,即
ΑTΑ=QR;
(7)
将式(7)两端左乘矩阵QT可得
QTΑTΑ=R;
(8)
因此式(6)两端左乘矩阵QT可以表示为
Rx=QTΑTb。
(9)
利用Givens变换可以实现矩阵A的QR分解,而Givens变换又可以利用CORDIC近似旋转算法实现。Volder 提出的CORDIC方法以其运算及硬件结构简单和多能性而倍受关注,并已广泛应用于信号处理领域[11-15]。典型的Givens变换矩阵为:

G为n×n的矩阵,令x=[x1…xi…xj…xn]T,向量x左乘矩阵G,表示将x的xi,xj旋转角度φ,转换完的向量为y=[y1…yi…yj…yn]T,可以得到
(10)
其他元素保持不变,选择合适的角度φ可以使yj=0。同样选择合适的G,可以将矩阵A转换成上三角矩阵。为了方便计算机计算,可以令 tanφ=2-k,k为整数。利用CORDIC算法近似实现矩阵的QR分解就是通过迭代不同的旋转角度,每次迭代旋转的角度为2的整数幂,最终可将yj转换为0。CORDIC 算法的收敛性满足收敛定理,其中第k次迭代为[16]:
(11)

(12)
变换过程如图2所示。

图2 基于CORDIC近似旋转算法的Givens变换示意
通过一系列变换,式(6)最终可以变成:
(13)
最终可以求解出未知向量
(14)
3 实验结果与分析
将接收机天线放置在基准点上收取GPS信号,接收到的可见卫星为7颗,分别将接收到的卫星伪距和电文存储下来,利用Matlab软件处理存储的数据。
对存储数据分别用求逆最小二乘算法和基于CORDIC近似QR分解的迭代最小二乘算法进行定位解算。在利用CORDIC近似QR分解的最小二乘算法时,迭代次数大于7得到的定位精度与求逆最小二乘算法基本一致。图3和图4给出了CORDIC近似旋转最小二乘算法在迭代次数为6和7时的定位精度与求逆最小二乘算法的定位精度对比,其中迭代初始点都为坐标原点。可以看出在迭代次数为7时,基于CORDIC近似旋转最小二乘算法定位精度很接近。迭代次数为6时,基于CORDIC近似旋转最小二乘算法定位精度虽然也很高,但没有特别稳定。

图3 垂直定位误差绝对值

图4 水平定位误差绝对值
在单次定位解算中,最小二乘求逆算法和迭代最小二乘算法的运算量是不一样的,如果矩阵求逆采用常用的初等变换方法实现,迭代最小二乘算法采用本文给出的方法,可以得到每种算法的运算量,具体如表1所示。根据计算机原理可知,计算机操作的运算复杂度排序为:移位运算<加法运算<乘法运算<除法运算。
表1 不同算法运算量对比

运算初等变换求逆迭代QR分解(itg=6)迭代QR分解(itg=7)移位运算(次数)加运算(次数)乘运算(次数)除运算(次数)0969616727864849064
4 结束语
利用迭代最小二乘算法进行定位解算时,迭代次数越多,达到的精度越高,同时运算量也会相应增加。但在不影响定位精度的前提下,迭代最小二乘算法的运算量不管是在数量还是复杂度上都要优于传统最小二乘算法,从而有效地提高了数据处理器的运算效率。另外,利用CORDIC算法对观测矩阵进行QR分解代替求逆运算,能够减少大量运算,这对载波相位差分以及定向解算也具有很大的参考意义。
[1] Mosavi M R,Azarshahi S,Emamgholipour I,et al.Least Squares Techniques for GPS Receivers Positioning Filter using Pseudo-Range and Carrier Phase Measurements[J].Iranian Journal of Electrical & Electronic Engineering,2014,10(1):18-26.
[2] He Yuheng,Martin R,Bilgic A M.Approximate Iterative Least Squares Algorithms for GPS Positioning[C]∥ IEEE International Symposium on Signal Processing and Information Technology,2011:231-236.
[3] Rahemi N,Mosavi M R,Abedi A A,et al.Accurate Solution of Navigation Equations in GPS Receivers for Very High Velocities Using Pseudorange Measurements[J].Advances in Aerospace Engineering,2014(2):1-8.
[4] 李春华,蔡成林,梁愈高,等.一种高精度的北斗伪距单点定位加权算法[J].测绘科学,2015,40(9):33-38.
[5] 徐飞,肖铁军,华纯,等.基于FPGA的视频图像旋转硬件加速器的设计与实现[J].传感器与微系统,2010,29(10):100-102.
[6] Meher P K,Sang Y P.CORDIC Designs for Fixed Angle of Rotation[J].IEEE Transactions on Very Large Scale Integration Systems,2013,21(2):217-228.
[8] 张朝柱,韩吉南,燕慧智.高速高精度固定角度旋转CORDIC算法的设计与实现[J].电子学报,2016,44(2):485-490.
[9] Ramadoss R,Kermani M M,Azarderakhsh R.Reliable Hardware Architectures of the CORDIC Algorithm With a Fixed Angle of Rotations[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2017,64(8):972-976.
[10] He Y,Bilgic A.Iterative Least Squares Method for Global Positioning System[J].Advances in Radio Science,2011,9(1):203-208.
[11] Biswas D,Maharatna K.A CORDIC-Based Low-Power Statistical Feature Computation Engine for WSN Applications[J].Circuits Systems & Signal Processing,2015,34(12):4011-4028.
[12] Torres V,Valls J,Canet M J.Optimised CORDIC-based Atan2 Computation for FPGA Implementations[J].Electronics Letters,2017,53(19):1296-1298.
[13] Aggarwal S,Meher P K,Khare K.Concept,Design,and Implementation of Reconfigurable CORDIC[J].IEEE Transactions on Very Large Scale Integration Systems,2016,24(4):1588-1592.
[14] Chen Jiyang,Lei Yuanwu,Peng Yuanxi,et al.Configurable Floating-Point FFT Accelerator on FPGA Based Multiple-Rotation CORDIC[J].Chinese Journal of Electronics,2016,25(6):1063-1070.
[15] Heidarpour M,Ahmadi A,Rashidzadeh R.A CORDIC Based Digital Hardware For Adaptive Exponential Integrate and Fire Neuron[J].IEEE Transactions on Circuits & Systems.Part I:Regular Papers,2016,63(11):1986-1996.
[16] Nawandar N K,Garg B,Sharma G K.RICO:A Low Power Repetitive Iteration CORDIC for DSP Applications in Portable Devices[J].Journal of Systems Architecture,2016,70:82-92.
[17] 史方显,曾立,陈昱,等.改进型高速高精度CORDIC算法及其在DDFS中的应用[J].电子学报,2017,45(2):446-451.
