Hilbert空间中一类广义的Ishikawa迭代及其在变分不等式中的应用

王 涛，郭 科，赵世莲

(西华师范大学 数学与信息学院，四川 南充 637009)

0 引 言

H指的是一个具有内积〈.,.〉和范数‖·‖的实Hilbert空间，T：H→H，T的不动点集为

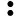
我们称T是一个压缩映射，若存在0<α<1有

‖Tx-Ty‖≤α‖x-y‖， ∀x，y∈H，

称T：H→H是非扩张映射，若

‖Tx-Ty‖≤‖x-y‖， ∀x，y∈H。

在这篇文章中，我们的目的是找到定义在H上的映射T的不动点。该问题的相关研究结果有很多，特别地，由压缩映像原理[1]可知，当T为压缩映射时，给定某个x1∈H，考虑迭代

xn+1=Txn∀n=1,2,…，

此时，{xn}n∈N弱收敛于T的不动点。

由于T是压缩映射这一条件较难满足，因此，对于T为非扩张映射的情形，文献[2-3]提出了Krasnoselskii-Mann迭代。任意给定x1∈H，存在某个适当的λ∈[0,1]，递推关系为

xn+1=(1-λ)xn+λTxn， ∀n=1,2,…，

之后，Reich[4]在此基础上将λ变成λn∈[0,1]，提出了更为一般的迭代

xn+1=(1-λn)xn+λnTxn， ∀n=1,2,…，

并且，在下述两个条件成立的情况下，{xn}n∈N弱收敛到T的一个不动点，

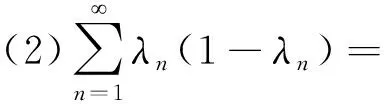
最近，Christian Kanzow和他的合作者共同提出了一种广义的Krasnoselskii-Mann迭代[5]，其迭代格式如下：

xn+1=αnxn+βnTxn， ∀n=1,2,…，

其中{αn},{βn}是[0,1]上的实序列且满足αn+βn≤1，∀n=1,2,…。如果以下两个条件成立，则通过该迭代产生的序列{xn}弱收敛到T的不动点：

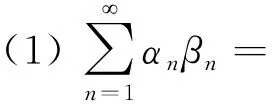
而Shiro-Ishikawa[6]在Krasnoselskii-Mann之后获得了一种形式上更具一般性，应用上具有更强的适应性[7]的迭代，该迭代过程为

xn+1=(1-αn)xn+αnT[(1-βn)xn+βnTxn]， ∀n=1,2,…，

其中{αn}和{βn}均属于[0,1]。显然 ，当βn≡0时，Ishikawa迭代就为Krasnoselskii-Mann迭代。所以，我们借助文献[5]的思想，提出如下广义的Ishikawa迭代，该迭代过程为

xn+1=αnxn+βnT(snxn+tnTxn)， ∀n=1,2,…，

其中{αn},{βn},{sn},{tn}是[0,1]上的实序列，并且αn+βn1，sn+tn1。在适当的条件下，我们证明了该算法弱收敛到T的一个不动点。

本文的第二部分给出相关的定义和定理。而第三部分给出了本文的主要结果，并对算法收敛性进行了证明。在第四部分，将本文提出的广义Ishikawa迭代算法应用到了求解变分不等式问题。

1 预备知识

在本部分，我们首先给出一些收敛性证明需要用到的基本知识。下面这个引理在弱收敛的证明中扮演着重要作用。

引理2[5]H是实Hilbert空间，则：

(a)‖x+y‖2≤‖x‖2+2〈y,x+y〉,∀x,y∈H，

(b)‖tx+sy‖2=t(t+s)‖x‖2+s(t+s)‖y‖2-st‖x-y‖2,∀x,y∈H,∀s,t∈。

引理3[9]有界点列必存在弱收敛的子列。

引理4[9]在Hilbert空间H中，若H中的点列{xn}弱收敛到x，则∀y≠x，

引理5[10]若T为非扩张映射，{xn}弱收敛到x，{(I-T)xn}强收敛到y，则(I-T)x=y。

为了给出下一个引理，在此，我们介绍两个概念，分别叫做投影和变分不等式。

K是H的一个非空闭凸子集，对于任意u∈H，存在唯一的一点PKu∈K使得

‖u-PKu‖≤‖u-y‖，∀y∈K，

PKu就叫做从H到K的投影。很明显，PK是一个非扩张映射。

K是H中的非空闭凸子集，F：H→H，变分不等式VI(K,F)是指，寻找x*∈K使得

〈F(x*)，y-x*〉≥0 ∀y∈K。

引理6 若K⊂H是一个闭凸集，F:K→H是一个映射，则

x∈SOL(K,F)⟺‖rt(x)‖=0，∀t>0，

其中SOL(K,F)表示变分不等式VI(K,F)的解集，rt(x)=x-PK(x-tF(x))称为自然残差函数。

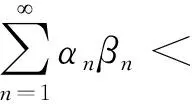
定义1设F：H→H，称F在H上是α余强制的，若存在常数α>0使得

〈F(x)-F(y)，x-y〉≥α‖F(x)-F(y)‖2， ∀x,y∈H。

定义2称数列{βn}一致大于0指的是该数列存在严格大于0的下界，即存在正数β，使得

βn>β>0,∀n=1,2,…。

2 主要结果

定理1T:H→H是一个非扩张映射使得其不动点集F(T)非空，x1∈H，序列{xn}由如下迭代产生

xn+1=αnxn+βnT(snxn+tnTxn),∀n=1,2,…，

若{αn},{βn},{sn},{tn}是[0,1]上的实序列，其中{βn}一致大于0，对所有n≥1均有αn+βn1,sn+tn≤1，并且以下条件成立：；；；，

则序列{xn}弱收敛到T的不动点。

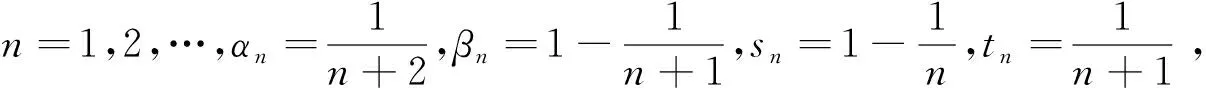
证明

‖xn+1-x*‖

=‖αnxn+βnT(snxn+tnTxn)-x*‖

=‖αn(xn-x*)+βn(T(snxn+tnTxn)-x*)+(αn+βn-1)x*‖

≤αn‖xn-x*‖+βn‖T(snxn+tnTxn)-x*‖+(1-αn-βn)‖x*‖

≤αn‖xn-x*‖+βn‖snxn+tnTxn-x*‖+(1-αn-βn)‖x*‖

=αn‖xn-x*‖+βn‖sn(xn-x*)+tn(Txn-x*)+(sn+tn-1)x*‖+(1-αn-βn)‖x*‖

≤αn‖xn-x*‖+βn[sn‖xn-x*‖+tn‖Txn-x*‖+(1-sn-tn)‖x*‖]+(1-αn-βn)‖x*‖

=αn‖xn-x*‖+βn[sn‖xn-x*‖+tn‖Txn-Tx*‖+(1-sn-tn)‖x*‖]+(1-αn-βn)‖x*‖

≤αn‖xn-x*‖+βn[sn‖xn-x*‖+tn‖xn-x*‖+(1-sn-tn)‖x*‖]+(1-αn-βn)‖x*‖

=αn‖xn-x*‖+βn[(sn+tn)‖xn-x*‖+(1-sn-tn)‖x*‖]+(1-αn-βn)‖x*‖

≤αn‖xn-x*‖+βn[‖xn-x*‖+(1-sn-tn)‖x*‖]+(1-αn-βn)‖x*‖

=(αn+βn)‖xn-x*‖+βn(1-sn-tn)‖x*‖+(1-αn-βn)‖x*‖

≤‖xn-x*‖+[βn(1-sn-tn)+(1-αn-βn)]‖x*‖

(1)

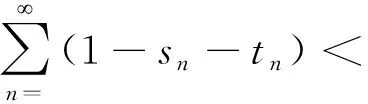
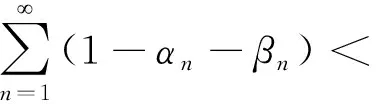
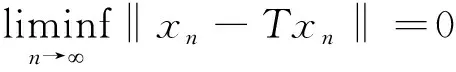
‖xn+1-x*‖2

=‖αnxn+βnT(snxn+tnTxn)-x*‖2

=‖αn(xn-x*)+βn(T(snxn+tnTxn)-x*)+(αn+βn-1)x*‖2

≤‖αn(xn-x*)+βn(T(snxn+tnTxn)-x*)‖2+2〈(αn+βn-1)x*，xn+1-x*〉

≤αn(αn+βn)‖xn-x*‖2+βn(αn+βn)‖T(snxn+tnTxn)-x*‖2-

αnβn‖xn-T(snxn+tnTxn)‖2+2〈(αn+βn-1)x*，xn+1-x*〉

≤αn‖xn-x*‖2+βn‖T(snxn+tnTxn)-x*‖2+2〈(αn+βn-1)x*，xn+1-x*〉

≤αn‖xn-x*‖2+βn‖T(snxn+tnTxn)-x*‖2+2(1-αn-βn)‖x*‖‖xn+1-x*‖

(2)

由第一步知{xn}有界，所以存在M1≥2‖x*‖‖xn+1-x*‖，又T是非扩张映射，x*∈F(T)，由(2)式得

‖xn+1-x*‖2

≤αn‖xn-x*‖2+βn‖T(snxn+tnTxn)-Tx*‖2+(1-αn-βn)M1

≤αn‖xn-x*‖2+βn‖snxn+tnTxn-x*‖2+(1-αn-βn)M1

=αn‖xn-x*‖2+βn‖sn(xn-x*)+tn(Txn-x*)+(sn+tn-1)x*‖2+(1-αn-βn)M1

≤αn‖xn-x*‖2+βn[‖sn(xn-x*)+tn(Txn-x*)‖2+2〈(sn+tn-1)x*，snxn+tnTxn-x*〉]+

(1-αn-βn)M1

≤αn‖xn-x*‖2+βn[‖sn(xn-x*)+tn(Txn-x*)‖2+2(1-sn-tn)‖x*‖‖snxn+tnTxn-x*‖]+

(1-αn-βn)M1

≤αn‖xn-x*‖2+βn[sn(sn+tn)‖xn-x*‖2+tn(sn+tn)‖Txn-x*‖2-sntn‖xn-Txn‖2+

2(1-sn-tn)‖x*‖‖snxn+tnTxn-x*‖]+(1-αn-βn)M1

=αn‖xn-x*‖2+βn[sn(sn+tn)‖xn-x*‖2+tn(sn+tn)‖Txn-Tx*‖2-sntn‖xn-Txn‖2+

2(1-sn-tn)‖x*‖‖snxn+tnTxn-x*‖]+(1-αn-βn)M1

≤αn‖xn-x*‖2+βn[sn(sn+tn)‖xn-x*‖2+tn(sn+tn)‖xn-x*‖2-sntn‖xn-Txn‖2+

2(1-sn-tn)‖x*‖‖snxn+tnTxn-x*‖]+(1-αn-βn)M1

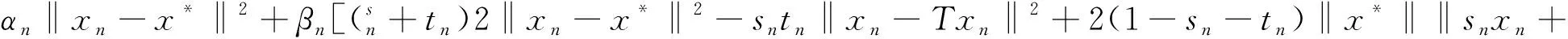
tnTxn-x*‖]+(1-αn-βn)M1

≤αn‖xn-x*‖2+βn[‖xn-x*‖2-sntn‖xn-Txn‖2+2(1-sn-tn)‖x*‖‖snxn+tnTxn-x*‖]+

(1-αn-βn)M1

=(αn+βn)‖xn-x*‖2-βnsntn‖xn-Txn‖2+2βn(1-sn-tn)‖x*‖‖snxn+tnTxn-x*‖+

(1-αn-βn)M1

≤‖xn-x*‖2-βnsntn‖xn-Txn‖2+2βn(1-sn-tn)‖x*‖ ‖snxn+tnTxn-x*‖+(1-αn-βn)M1

(3)

因为

‖snxn+tnTxn-x*‖

=‖sn(xn-x*)+tn(Txn-x*)+(sn+tn-1)x*‖

≤sn‖xn-x*‖+tn‖Txn-x*‖+(1-sn-tn)‖x*‖

=sn‖xn-x*‖+tn‖Txn-Tx*‖+(1-sn-tn)‖x*‖

≤sn‖xn-x*‖+tn‖xn-x*‖+(1-sn-tn)‖x*‖

=(sn+tn)‖xn-x*‖+(1-sn-tn)‖x*‖

≤‖xn-x*‖+(1-sn-tn)‖x*‖

≤‖xn-x*‖+‖x*‖

所以由{xn}的有界性知，存在M2≥2‖x*‖‖snxn+tnTxn-x*‖，进一步由(3)得，

‖xn+1-x*‖2≤‖xn-x*‖2-βnsntn‖xn-Txn‖2+βn(1-sn-tn)M2+(1-αn-βn)M1，

βnsntn‖xn-Txn‖2≤‖xn-x*‖2-‖xn+1-x*‖2+βn(1-sn-tn)M2+(1-αn-βn)M1，

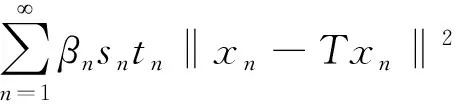
(4)

因为

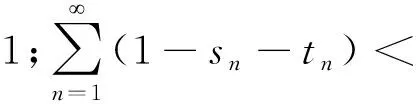
所以 (4)式右端

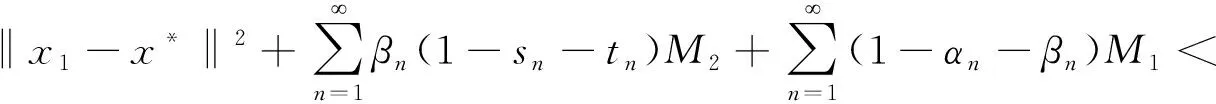
又因为{βn}一致大于零，即存在β使得βn>β>0，∀n=1，2,…，所以，βnsntn>βsntn，∀n=1,2,…，进一步可得

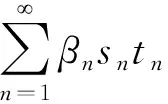
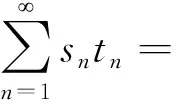
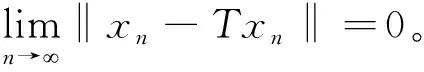
‖Txn+1-xn+1‖

=‖Txn+1-αnxn-βnTyn‖

=‖βn(Txn+1-Tyn)+αn(Txn+1-xn)+(1-αn-βn)Txn+1‖

≤βn‖Txn+1-Tyn‖+αn‖Txn+1-xn‖+(1-αn-βn)‖Txn+1‖

≤βn‖xn+1-yn‖+αn‖Txn+1-xn‖+(1-αn-βn)‖Txn+1‖

=βn‖αnxn+βnTyn-yn‖+αn‖Txn+1-xn‖+(1-αn-βn)‖Txn+1‖

=βn‖βn(Tyn-yn)+αn(xn-yn)-(1-αn-βn)yn‖+αn(‖Txn+1-xn+1+xn+1-xn‖)+

(1-αn-βn)‖Txn+1‖

≤βn(βn‖Tyn-yn‖+αn‖xn-yn‖+(1-αn-βn)‖yn‖)+αn(‖Txn+1-xn+1‖+‖xn+1-xn‖)+

(1-αn-βn)‖Txn+1‖

=βn(βn‖Tyn-yn‖+αn‖xn-yn‖+(1-αn-βn)‖yn‖)+αn(‖Txn+1-xn+1‖+

‖αnxn+βnTyn-xn‖)+(1-αn-βn)‖Txn+1‖

=βn(βn‖Tyn-yn‖+αn‖xn-yn‖+(1-αn-βn)‖yn‖)+αn(‖Txn+1-xn+1‖+

‖βn(Tyn-xn)+(αn+βn-1)xn‖)+(1-αn-βn)‖Txn+1‖

≤βn(βn‖Tyn-yn‖+αn‖xn-yn‖+(1-αn-βn)‖yn‖)+αn(‖Txn+1-xn+1‖+

βn‖Tyn-xn‖+(1-αn-βn)‖xn‖)+(1-αn-βn)‖Txn+1‖

=βn(βn‖Tyn-yn‖+αn‖xn-yn‖)+αn(‖Txn+1-xn+1‖+βn‖Tyn-xn‖)+

(1-αn-βn)(βn‖yn‖+αn‖xn‖+‖Txn+1‖)

移项得，

(1-αn)‖Txn+1-xn+1‖≤βn(βn‖Tyn-yn‖+αn‖xn-yn‖)+αnβn‖Tyn-xn‖+

(1-αn-βn)(βn‖yn‖+αn‖xn‖+‖Txn+1‖)

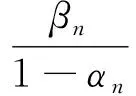
‖Txn+1-xn+1‖

=βn‖Tyn-snxn-tnTxn‖+αn(‖xn-yn‖+‖Tyn-xn‖)+

=βn‖tn(Tyn-Txn)+sn(Tyn-xn)+(1-sn-tn)Tyn‖+αn(‖xn-yn‖+‖Tyn-xn‖)+

≤βn(tn‖Tyn-Txn‖+sn‖Tyn-xn‖+(1-sn-tn)‖Tyn‖)+αn(‖xn-yn‖+‖Tyn-xn‖)+

≤βn(tn‖yn-xn‖+sn‖Tyn-xn‖+(1-sn-tn)‖Tyn‖)+αn(‖xn-yn‖+‖Tyn-xn‖)+

=(βntn+αn)‖xn-yn‖+(βnsn+αn)‖Tyn-xn‖+βn(1-sn-tn)‖Tyn‖+

=(βntn+αn)‖xn-(snxn+tnTxn)‖+(βnsn+αn)‖Tyn-xn‖+βn(1-sn-tn)‖Tyn‖+

=(βntn+αn)‖tn(xn-Txn)+(1-sn-tn)xn‖+(βnsn+αn)‖Tyn-xn‖+βn(1-sn-tn)‖Tyn‖+

≤tn(βntn+αn)‖xn-Txn‖+(βntn+αn)(1-sn-tn)‖xn‖+(βnsn+αn)(‖Tyn-Txn‖+‖Txn-xn‖)+

≤tn(βntn+αn)‖xn-Txn‖+(βntn+αn)(1-sn-tn)‖xn‖+(βnsn+αn)(‖yn-xn‖+‖Txn-xn‖)+

=tn(βntn+αn)‖xn-Txn‖+(βntn+αn)(1-sn-tn)‖xn‖+(βnsn+αn)(‖snxn+tnTxn-xn‖+

=tn(βntn+αn)‖xn-Txn‖+(βntn+αn)(1-sn-tn)‖xn‖+

(βnsn+αn)(‖tn(Txn-xn)+(tn+sn-1)xn‖+

≤tn(βntn+αn)‖xn-Txn‖+(βntn+αn)(1-sn-tn)‖xn‖+

(βnsn+αn)(tn‖Txn-xn‖+(1-tn-sn)‖xn‖+‖Txn-xn‖)+βn(1-sn-tn)‖Tyn‖+

=(tn(βntn+αn)+(βnsn+αn)(tn+1))‖Txn-xn‖+(βntn+αn)(1-sn-tn)‖xn‖+

(βnsn+αn)(1-sn-tn)‖xn‖+βn(1-sn-tn)‖Tyn‖+

=(tn2βn+tnαn+βnsntn+βnsn+αntn+αn)‖Txn-xn‖+(βntn+αn)(1-sn-tn)‖xn‖+

(βnsn+αn)(1-sn-tn)‖xn‖+βn(1-sn-tn)‖Tyn‖+

=((tn+sn)βntn+βnsn+2αntn+αn)‖Txn-xn‖+(βntn+αn)(1-sn-tn)‖xn‖+

(βnsn+αn)(1-sn-tn)‖xn‖+βn(1-sn-tn)‖Tyn‖+

≤(βntn+βnsn+2αntn+αn)‖Txn-xn‖+2(1-sn-tn)‖xn‖+(1-sn-tn)‖Tyn‖+

≤(βn+2αntn+αn)‖Txn-xn‖+2(1-sn-tn)‖xn‖+(1-sn-tn)‖Tyn‖+

≤(1+2αntn)‖Txn-xn‖+2(1-sn-tn)‖xn‖+(1-sn-tn)‖Tyn‖+

由{xn}有界知，存在M使得‖xn‖≤M。又因为T为非扩张映射且T的不动点集F(T)非空，所以{Txn}有界。因为‖Txn-xn‖≤‖Txn‖+‖xn‖，所以存在M3，使得‖Txn-xn‖≤M3，即{‖Txn-xn‖}有界。又因为yn=snxn+tnTxn，{xn}有界，{Txn}有界，0≤sn+tn≤1，所以{yn}有界。

同理得{Tyn}有界，即存在M4，使得‖Tyn‖≤M4。

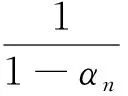
(5)

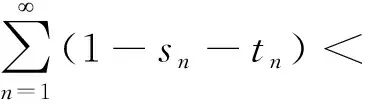
第四步：说明{xn}弱收敛到T的不动点。

由第一步知{xn}有界，则根据引理3得，{xn}存在弱收敛的子列。假设{xn}的子列{xnj}弱收敛到p1。

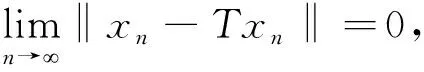
(反证法)假设还存在{xn}的子列{xmj}弱收敛到p2，且p2≠p1，且由以上分析可知p2为T的不动点。

以上关系得出矛盾，即可得{xn}的子列弱收敛到同一个弱聚点。综上可得，{xn}弱收敛到T的不动点。

3 应 用

在这部分，我们根据得到的广义Ishikawa迭代及其收敛性，可得出一种求解变分不等式VI(K,F)的方法。 由引理6可知，x*为变分不等式的解，等价于对∀t>0，‖rt(x*)‖=0，也即为x*=PK(x*-tF(x*))。此时，x*就是映射PK(x-tF(x))的不动点。所以，求解变分不等式VI(K,F)，就是寻找PK(x-tF(x))的不动点。

定理2K是H的一个非空闭凸子集，F：H→H是α余强制的并且SOL(K,F)非空，0

yn=snxn+tnPK(xn-tF(xn))，

xn+1=αnxn+βnPK(yn-tF(yn))，

若{αn},{βn},{sn},{tn}是[0,1]上的实序列，其中{βn}一致大于0，对所有n≥1均有αn+βn≤1，sn+tn≤1，并且以下条件成立

则序列{xn}弱收敛到变分不等式VI(K,F)的解。

证明

首先需说明PK(x-tF(x))是非扩张映射，即证明对t>0，x≠y

‖PK(x-tF(x))-PK(y-tF(y))‖≤‖x-y‖，

因为PK是一个非扩张的映射，即得对t>0，∀x,y∈H

‖PK(x-tF(x))-PK(y-tF(y))‖≤‖(x-y)-t(F(x)-F(y))‖，

所以要证PK(x-tF(x))是非扩张映射，只需证对t>0，∀x,y∈H

‖(x-y)-t(F(x)-F(y))‖≤‖x-y‖ 。

(6)

(6)⟺‖(x-y)-t(F(x)-F(y))‖2≤‖x-y‖2，

⟺‖x-y‖2+‖t(F(x)-F(y))‖2-2〈t(F(x)-F(y)),x-y〉≤‖x-y‖2，

⟺t‖F(x)-F(y)‖2≤2〈F(x)-F(y),x-y〉，

(7)

因为F在H上是α余强制的，即可得

〈F(x)-F(y)，x-y〉≥α‖F(x)-F(y)‖2， ∀x,y∈H，

(8)

又因为0

参考文献：

[1] 张恭庆,林源渠.泛函分析讲义.上册[M].北京：北京大学出版社,2005.

[2] KRASNOSEL M A.Two remarks on the method of successive approximations[J].Usp.Mat.Nauk10,1955,1(63):123-127.

[3] MANN W R.Mean value methods in iteration[J].Proceedings of the American Mathematical Society,1953,4(3):506-510.

[4] REICH S.Weak convergence theorems for nonexpansive mappings in Banach spaces[J].Journal of Mathematical Analysis & Applications,1979,67(2):274-276.

[5] KANZOW C,SHEHU Y.Generalized Krasnoselskii-Mann-type iterations for nonexpansive mappings in Hilbert spaces[M].Netherlands:Kluwer Academic Publishers,2017:1-26.

[6] ISHIKAWA S.Fixed points by a new iteration method[J].Proceedings of the American Mathematical Society,1974,44(1):147-150.

[7] 游兆永,徐宗本.Ishikawa迭代法的收敛性及其与Mann迭代法的比较[J].工程数学学报,1984,4(2):136-138.

[8] AUSLENDER A,TEBOULLE M,BENTIBA S.A logarithmic-quadratic proximal method for variational inequalities[M].Netherlands:Kluwer Academic Publishers,1999:31-40.

[9] BAUSCHKE H H,COMBETTES P L.Convex analysis and monotone operator theory in Hilbert space[M].New York:Springer New York,2011:287-316.

[10] BRODER F E.Convergence theorems for sequences of nonlinear operators in Banach spaces[J].Mathematische Zeitschrift,1967,100(3):201-225.