关于Sp空间上加权复合算子的有界性
2018-07-05林庆泽刘军明吴玉田
林庆泽,刘军明,吴玉田
(1.广东工业大学 应用数学学院, 广州 510520;2.广东金融学院 金融数学与统计学院,广州 510520)
0 引言
当1≤p<∞时,用Hp表示复平面单位圆盘Δ上解析函数f组成的Hardy空间,其中
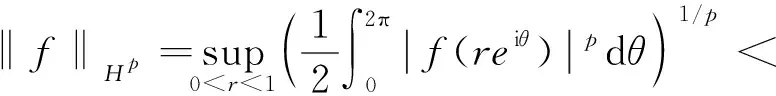
当p=∞时,H表示复平面单位圆盘Δ上有界解析函数f组成的空间,其范数定义为:
‖f‖
Sp为f ′属于Hardy空间Hp的复平面单位圆盘Δ上所有解析函数f组成的空间,其范数定义为:
‖f‖Sp=|f(0)|+‖f ′‖Hp。
容易验证Sp是一个Banach空间。 记H(Δ)表示单位圆盘Δ上所有解析函数组成的函数空间。 若φ,ø,f∈H(Δ)且φ(Δ)⊂Δ,则将算子Wφ,ø∶fa、i(f∘φ)称为加权复合算子。
加权复合算子Wφ,ø作用在各种不同的函数空间上近年来一直是一个非常热门的研究方向。 文献[1-2]研究了加权复合算子Wφ,ø作用在Hardy空间上的有界性等性质。 文献[3-4]还研究了Wφ,ø作用在不同Bergman空间之间和不同Hardy空间之间的有界性和紧性等性质。 文献[5-7]研究了加权复合算子Wφ,ø作用在Bloch型空间上的有界性、紧性和本性范数等性质。
加权复合算子的研究来源是多方面的,其中最典型的是文献[8]证明了H1空间上的线性等距变换都是加权复合算子,紧接着Forelli在文献[9]中证明了当1≤p<∞,p≠2时,在Hp空间上也有同样的结论。 文献[10]也证明了Sp空间上的类似结论。 在加权Bergman空间上,文献[11]得到了线性等距变换可以表示为加权复合算子的结论。
在加权复合算子Wφ,ø中,如果φ(z)=z,则得到乘法算子Mø∶fa、if;如果令ø≡1,则得到复合算子Cφ∶fa∘ φ。 近几十年,这两种算子在各种不同的函数空间上的有界性和紧性等性质一直是非常热门的研究方向,可参考文献[12-14]。而在Sp空间上的复合算子的研究则开始于Roan的文献[15]。 随后,MacCluer在文献[16]中用Carleson测度刻画了Sp空间上的复合算子的有界性和紧性。 一个非常有意义的创新是文献[17]将Sp空间上的加权复合算子的有界性和紧性的研究转化为Hp空间上的加权复合算子的有界性和紧性的研究。
本文受文献[18]的启发,给出了当φ是Δ上的共形满射时该加权复合算子Wφ,ø在Sp空间上的有界性的充要条件,从而推广了文献[18]的结论。
1 加权复合算子Wφ,ø在Sp空间上的有界性
由文献[19]可知,当1≤p≤∞时,Sp到圆盘代数Α上的嵌入映射是有界的且存在某个与p有关的常数kp>1,使得对于任意的f∈Sp,‖f‖≤kp‖f‖Sp。 下面的引理可参考文献[20]:
引理1 若φ是Δ上的解析函数且φ(Δ)⊂Δ,p>0,则对于∀f∈Hp,都有
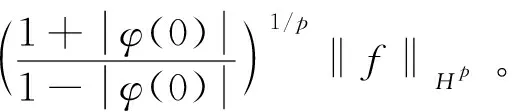
我们证明下面的命题。
命题1 若1≤p≤∞,当φ是Δ上的共形满射,f,g∈Sp时,以下结论成立:
(1)φ′∈H∞;
(2)存在某个与p有关的常数cp,φ>0,使得‖f∘ φ‖Sp≤cp,φ‖f‖Sp;
(3)‖fg‖Sp≤3(kp)2‖f‖Sp‖g‖Sp。
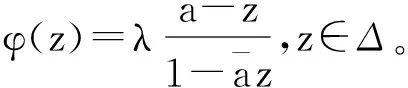
(2)当p=∞时,不等式是显然的。 现考虑1≤p<∞的情况。 由引理1,我们有
‖f∘φ‖Sp=|f∘φ(0)|+‖(f∘φ)′‖Hp
≤‖f‖+‖φ′(f′∘φ)‖Hp
≤kp‖f‖Sp+‖φ′‖‖f′∘φ‖Hp
≤kp‖f‖Sp+‖φ′‖
≤kp‖f‖Sp+‖φ′‖
≤cp,φ‖f‖Sp。
其中,cp,φ=kp+ ‖φ′‖
(3)‖fg‖Sp=|f(0)g(0)|+‖(fg)′‖Hp
≤‖f‖‖g‖+‖f′g+fg′‖Hp
≤(kp)2‖f‖Sp‖g‖Sp+‖f′g‖Hp+‖fg′‖Hp
≤(kp)2‖f‖Sp‖g‖Sp+‖f′‖Hp‖g‖+‖g′‖Hp‖f‖
≤(kp)2‖f‖Sp‖g‖Sp+kp‖f‖Sp‖g‖Sp+kp‖g‖Sp‖f‖Sp
≤ 3(kp)2‖f‖Sp‖g‖Sp。
证毕。
由命题1(3)可推出,Sp对于函数的乘法运算构成一个Banach代数。
下面给出Sp空间中元素的基于有限零点的分解。
命题2 若1≤p<,f∈Sp,而ζ∈Δ是f的n阶零点,那么存在g∈Sp,使得g(ζ)≠0且f(z)=(z-ζ)ng(z),z∈Δ。
证明由ζ∈Δ是f的n阶零点,故存在g∈H(Δ),使得g(ζ)≠0且f(z)=(z-ζ)n·g(z),z∈Δ。 下面证明g∈Sp。
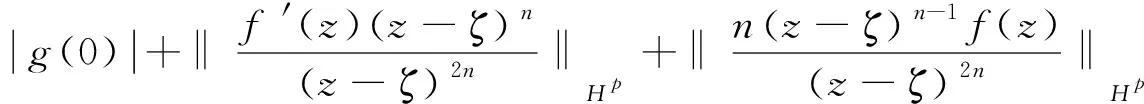
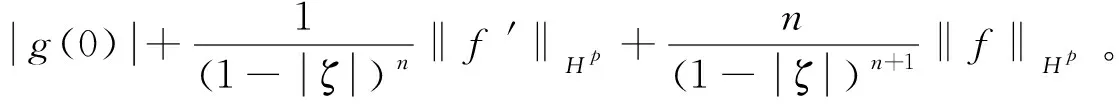
证毕。
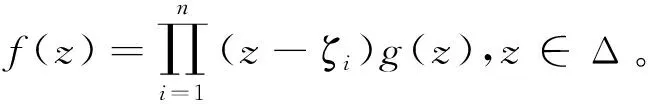
对于任意给定的z0∈Δ,由‖f‖≤kp‖f‖Sp可知,线性泛函Εz0∶fa(z0)作用在Sp(1≤p≤∞)空间上是有界的。 下面的推论给出了线性泛函Εz0与算子Mz-z0作用在Sp空间上的联系。
推论2 若1≤p<∞,当线性泛函Εz0与算子Mz-z0作用在Sp空间上时,有:
Ker(Εz0)=Ran(Mz-z0) 。
证明对于任意的f∈Ker(Εz0),由命题2,存在g∈Sp使得f(z)=(z-z0)g(z),z∈Δ,即f∈Ran(Mz-z0)。 反过来则是显然的。 证毕。
下面给出当φ是Δ上的共形满射时加权复合算子Wφ,ø在Sp空间上的有界性的充要条件。
定理1 当1≤p≤时,若φ,ø∈H(Δ),φ(Δ)⊂Δ,且φ是Δ上的共形满射,则加权复合算子Wφ,ø在Sp空间上是有界的当且仅当ø∈Sp。
证明若Wφ,ø是有界的,则取f=1,由‖φ‖Sp=‖Wφ,øf‖Sp≤‖Wφ,ø‖<∞,可知ø∈Sp。
现假设ø∈Sp,则由命题1,有
‖Wφ,øf‖Sp=‖øf∘φ‖Sp≤3(kp)2‖ø‖Sp‖f∘φ‖Sp≤3(kp)2‖ø‖Sp·cp,φ‖f‖Sp。
亦即Wφ,ø在Sp空间上是有界的。 证毕。
当取φ(z)=z,z∈Δ时,我们得到了关于乘法算子Mø在Sp空间上有界性的充分必要条件:
推论3 当1≤p≤∞时,若ø∈H(Δ),则乘法算子Mø在Sp空间上是有界的当且仅当ø∈Sp。
参考文献:
[1] ATTELE K R M.Multipliers of the range of composition operators[J].Tokyo J.Math.,1992,15(1):185-198.
[2] CONTRERAS M D,HERNANDEZ-DIAZ A G.Weighted composition operators on Hardy spaces[J].J.Math.Anal.Appl.,2001,263(1):224-233.
[3] CUCKOVIC Z,ZHAO R.Weighted composition operators on the Bergman space[J].J.London Math.Soc.,2004,70(2):499-511.
[4] CUCKOVIC Z,ZHAO R.Weighted composition operators between different weighted Bergman spaces and different Hardy spaces[J].Illinois Journal of Mathematics,2007,51(2):479-498.
[5] OHNO S,ZHAO R.Weighted composition operators on the Bloch space[J].Bull.Austral.Math.Soc.,2001,63(2):177-185.
[6] OHNO S,STROETHOFF K,ZHAO R.Weighted composition operators between Bloch-type spaces[J].Rocky Mountain J.Math.,2003,33(1):191-215.
[7] MACCLUER B D,ZHAO R.Essential norm of weighted composition operators between Bloch-type spaces[J].Rocky Mountain J.Math.,2003,33(4):1437-1458.
[8] DELEEUW K,RUDIN W,WERMER J.The isometries of some function spaces[J].Proc.Amer.Math.Soc.,1960,11(5):694-698.
[9] FORELLI F.The isometries of Hp[J].Canad.J.Math.,1964,16:721-728.
[10] NOVINGER W P,OBERLIN D M.Linear isometries of some normed spaces of analytic functions[J].Canad.J.Math.,1985,37(1):62-74.
[11] KOLASKI C J.Isometries of weighted Bergman spaces[J].Canad.J.Math.,1982,34(4):910-915.
[12] COWEN C C,MACCLUER B D.Composition operators on spaces of analytic functions[M].Boca Raton:CRC Press,1995.
[13] CLAHANE D D.Compact composition operators on weighted Bergman spaces of the unit ball[J].J.Operator Theory,2001,25(2):335-355.
[14] JARCHOW H,XIAO J.Composition operators between Nevanlinna classes and Bergman spaces with weights[J].J.Operator Theory,2001,46(3):605-618.
[15] ROAN R.Composition operators on the space of functions with Hp-derivative[J].Houston J.Math.,1978,4(3):423-428.
[16] MACCLUER B D.Composition operators on Sp[J].Houston J.Math.,1987,13(2):245-254.
[17] CONTRERAS M D,HERNANDEZ-DIAZ A G.Weighted composition operators on spaces of functions with derivative in Hardy space[J].J.Operator Theory,2004,52(1):173-184.
[18] ALLEN R F,HELLER K C,PONS M A.multiplication operator on S2(D)[J].Acta Sci.Math.(Szeged),2015,81(3/4):575-587.
[19] DUREN P L.Theory of Hp spaces[M].New York:Academic Press,1995.
[20] ZHU K H.Operator theory in function spaces[M].New York: Amer.Math.Soc.,2007.
