平均风与气弹效应一体化的桥梁非线性后颤振分析

吴长青， 张志田

(湖南大学土木工程学院风工程试验研究中心， 湖南 长沙 410082)

引 言

至今为止，大跨度桥梁的颤振稳定性仍以颤振临界风速是否大于颤振检验风速这一标准来评价，即当风速大于颤振临界值时，桥梁结构的响应将会快速发展并直至失稳破坏。受到这一标准的束缚，桥梁颤振后的运动状态与强健性问题一直未得到抗风设计者的广泛关注。1940年11月7日，原Tacoma桥在8级风的作用下，发生了剧烈的扭转振动，并在持续近70 min的大幅振动后因部分吊杆被拉断而最终导致桥面断裂坠入海湾。显然，原Tacoma桥经历了颤振失稳的过程，然而当前的评价标准与桥梁抗风理论无法对此给出合理的解释。从20世纪70年代未开始，针对飞机机翼断面的非线性气弹问题展开了大量的研究，结果表明机翼的颤振失稳特征并非发散，而是表现为明显的极限环振动(LCO)，且这种特征的振动状态强烈地依赖于结构的非线性与气弹非线性[1]。与机翼类似，桥梁的后颤振也是呈非线性特性的极限环振动问题，当风速超过颤振临界值时，结构的非线性特性与断面的非线性气弹特性共同决定了振幅的演变规律与LCO幅值。因此，要准确地评估桥梁的后颤振性能，必须建立一套非线性气弹稳定分析理论。

桥梁的后颤振问题是一类非线性气弹问题，涉及结构的几何非线性、材料非线性以及气动力非线性等，此外，颤振失稳是由非定常的气动自激力决定的，因此建立可靠的非线性非定常气动力模型是准确评估桥梁结构后颤振性能的关键所在。迄今已有的非线性气动力模型主要是针对于航空领域中的流线型断面。描述此类断面的非线性气动力特性主要有两大类方法，第一类是直接采用计算流体动力学的方法，让气流与结构的振动相耦合[2-4]。这一类方法不引入任何经验或者半经验模型，其可靠性取决于CFD 算法及湍流模型的可靠性，而且计算时间成本巨大。第二类方法是引入半经验模型来描述非线性气弹效应，比较典型的半经验模型有Tran和Petot提出的ONERA模型[5]，该模型已在直升机机翼、风力机叶片的动态失速问题中得到了广泛的应用[6-8]；Leishman和Beddoes也针对动态失速问题提出了一种半经验模型[9]；此外，丹麦Larsen等又提出了另一种专门用于描述大型风力机叶片的非线性气动力问题的半经验模型[10]。引入半经验模型是为了快速有效地描述断面的气动力性能，它们强调的是准确描述某一具体时候气动力的变化规律。流线型断面在动态失速状态下其前后缘涡的形成、发散、到分离均有良好的规律，然而桥梁断面具有明显的钝体特性，很难采用机翼理论中的半经验模型来描述其非线性气弹效应。

到目前为止，有关桥梁非线性气弹问题的研究还处于起步阶段。Diana等提出了一个非线性模型，它是以动态风攻角为变量的多项式函数，该模型可以描述频率与振幅相关的非线性效应[11]。Wu与Kareem提出了一种基于人工神经网络的非参数模型来捕捉气动系统的迟滞非线性行为[12]。后来，Wu与Kareem又提出了采用Volterra理论来描述非线性气动力效应[13]。上述提出的半经验模型均是描述给定振幅下一个运动周期内瞬时气动力的变化规律，它们不处理随运动振幅演变的气动力特性，然而在后颤振模拟中，准确地描述随振幅演变的气动力特性是至关重要的。

王骑等采用Taylor级数展开的方法提出了一种由不同谐波分量叠加的非线性气动力模型[14]，该模型描述的也是瞬时气动力随动态风攻角变化的非线性，并不能描述随振幅演变的气弹非线性。朱乐东与高广中[15]、Zhang与Xu[16]引入非线性颤振导数来描述结构后颤振幅值随时间的演变规律，该方法能描述气动自激力随振幅演变的非线性特性，但前提是要已知结构颤振后的响应时程。刘十一与葛耀君提出了采用附加的非线性微分方程组与附加的气动力自由度的方法来模拟气动力随振幅演变的非线性特性以及气动力的记忆效应[17]，这种方法不再采用动态攻角的概念，单独处理扭转运动导致的影响，但该法是对已知结果进行拟合且拟合参数数目很多。

在大跨度桥梁抗风分析中，通常将平均风效应、准定常气动效应、非定常气弹效应独立求解后再线性叠加[18-19]。然而，各类风荷载效应随着风速及结构姿态的变化均呈现出一种非线性性质[20-21]。当各种非线性效应比较显著时，叠加原理不再成立，从而需要一体化考虑平均风荷载、抖振力荷载及自激力荷载。与频域法相比，时域方法可综合考虑结构的几何、材料以及部分气动力非线性，因此时域法是模拟桥梁后颤振性能的必然选择。然而，在时域分析中将多种荷载一体化考虑后，会出现气动弹性模型与平均风荷载模型之间的不相容问题。

本文采用多阶段阶跃函数法来描述随振幅演变的非线性气动自激力。每个阶段的阶跃函数均是针对某一特定运动状态(以振幅表征)下识别的颤振导数拟合得到，它可以用来描述断面在这一特定运动状态下的气弹特性，如果一系列离散运动状态下的阶跃函数都可获取，那么随振幅演变的气动力非线性特性也可近似地确定。运动幅值的发展必然存在不同阶段阶跃函数间的切换问题，然而这种切换可能会引起结构的非物理瞬态响应，因此，笔者引入平行激励的求解策略来处理这一问题。此外，本文提出伪稳态(Pseudo-steady)效应分离法来解决气动自激力模型与平均风荷载模型之间不相容的问题。

1 线性单阶段自激力时域模型

桥梁断面的气动自激力通常采用Scanlan提出的时频混合模型来描述，正弦运动下单位长度主梁的气动自激升力与升力矩表达式如下[22]：

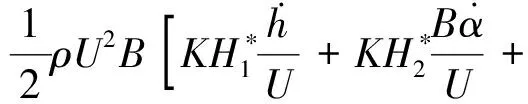
(1)

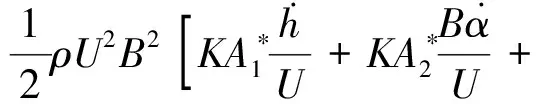
(2)

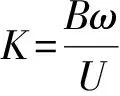
由于Scanlan自激力模型不能直接用于颤振时域分析，因此采用阶跃函数法拟合出与Scanlan模型等价的时域自激力模型。阶跃函数的概念源于经典机翼理论，用来描述风速或者风攻角突然改变时气动升力的瞬态演变过程，其表达式如下：

(3)

(4)

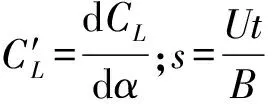
对于连续、任意的结构姿态变化过程，单位长度主梁的气动自激力可写成如下卷积形式(IF气动自激力模型)：

Lse(s)=Lsea(s)+Lseh(s)=

(5)

Mse(s)=Msea(s)+Mseh(s)=

(6)

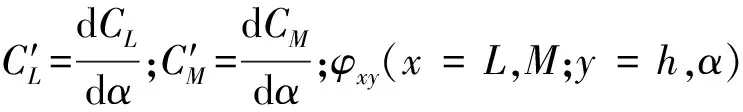
(7)

式中axyi与dxyi(x=L，M；y=h，α；i=1，2，3，…)为待识别的参数。

分别对公式(1),(2)与(5),(6)进行傅里叶变换，再根据频谱相等的原则可以得到颤振导数与阶跃函数之间的一些等式[23]，比如

(8)

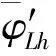
(9)

根据公式(9)建立的关系，通过求解以下函数的极小值来获取阶跃函数的参数值。

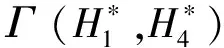
(10)

其余阶跃函数的参数值也可仿照上述的过程求得。

2 非线性多阶段自激力时域模型

公式(5)与(6)中涉及的阶跃函数(即公式(7)所示)是基于线性理论提出来的，它与结构的运动幅值无关，不能体现气动自激力随振幅演变的非线性特性。对于后颤振的非线性气弹问题，必须建立非线性的气动自激力模型。为了考虑气动力非线性，本文引入多阶段阶跃函数，它不仅是无量纲时间的函数，也是振幅的函数，表达式为

(11)

式中Ak(k=1，2，3，…)为第k阶振幅(竖向振幅hk或扭转振幅αk)；φxy(s,Ak)(x=L，M；y=h，α)为第k阶振幅对应的阶跃函数；其他符号的意义同前。如果足够多的离散振幅状态对应的阶跃函数均获得了，那么断面的非线性气弹特性也可确定。

在时域分析中，主梁不同部位的振幅不同，因而其运动状态对应的阶跃函数也不同。在桥梁某个断面达到LCO状态之前，其振幅是不断演变的，任意时刻t的振幅可用一组中间振幅状态来表示，如扭转振幅h*或扭转振幅α*

αk≤α*≤αk+1；hm≤h*≤hm+1

(12)

其中：k和k+1分别表示扭转振幅的第k和k+1阶，m和m+1表示扭转振幅的第m和m+1阶，对于这样的中间状态，其阶跃函数可通过线性插值得到:

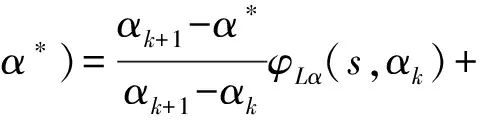
ηα,kφLα(s,αk)+ηα,k+1φLα(s,αk+1)

(13)

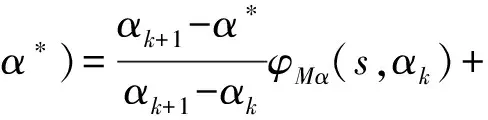
ηα,kφMα(s,αk)+ηα,k+1φMα(s,αk+1)

(14)

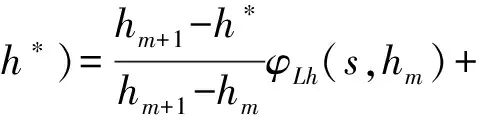
ηh,mφLh(s,hm)+ηh,m+1φLh(s,hm+1)

(15)

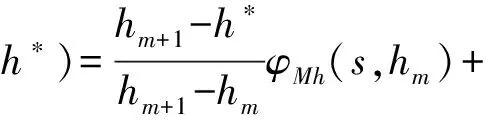
ηh,mφMh(s,hm)+ηh,m+1φMh(s,hm+1)

(16)

中间状态对应的气动自激力表达式如下：

Lse(s,α*,h*)=ηα,kLseα(s,αk)+

ηα,k+1Lseα(s,αk+1)+ηh,mLseh(s,hm)+

ηh,m+1Lseh(s,hm+1)

(17)

Mse(s,α*,h*)=ηα,kMseα(s,αk)+

ηα,k+1Mseα(s,αk+1)+ηh,mMseh(s,hm)+ηh,m+1Mseh(s,hm+1)

(18)

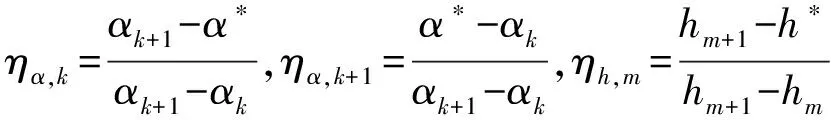
在时域分析中，突然切换一组新的阶跃函数参与计算时可能会引起非物理的瞬态响应，如图1所示。这种瞬态现象取决于识别的阶跃函数，如采用阶跃函数描述正弦运动引起的自激力时程时，在达到稳态的正弦形式的自激力之前，往往需要经过一个瞬态演变的过程，如图2所示。然而这一瞬态过程只是阶跃函数的拟合过程所引起的附带现象，并没有明显的物理意义[24]。

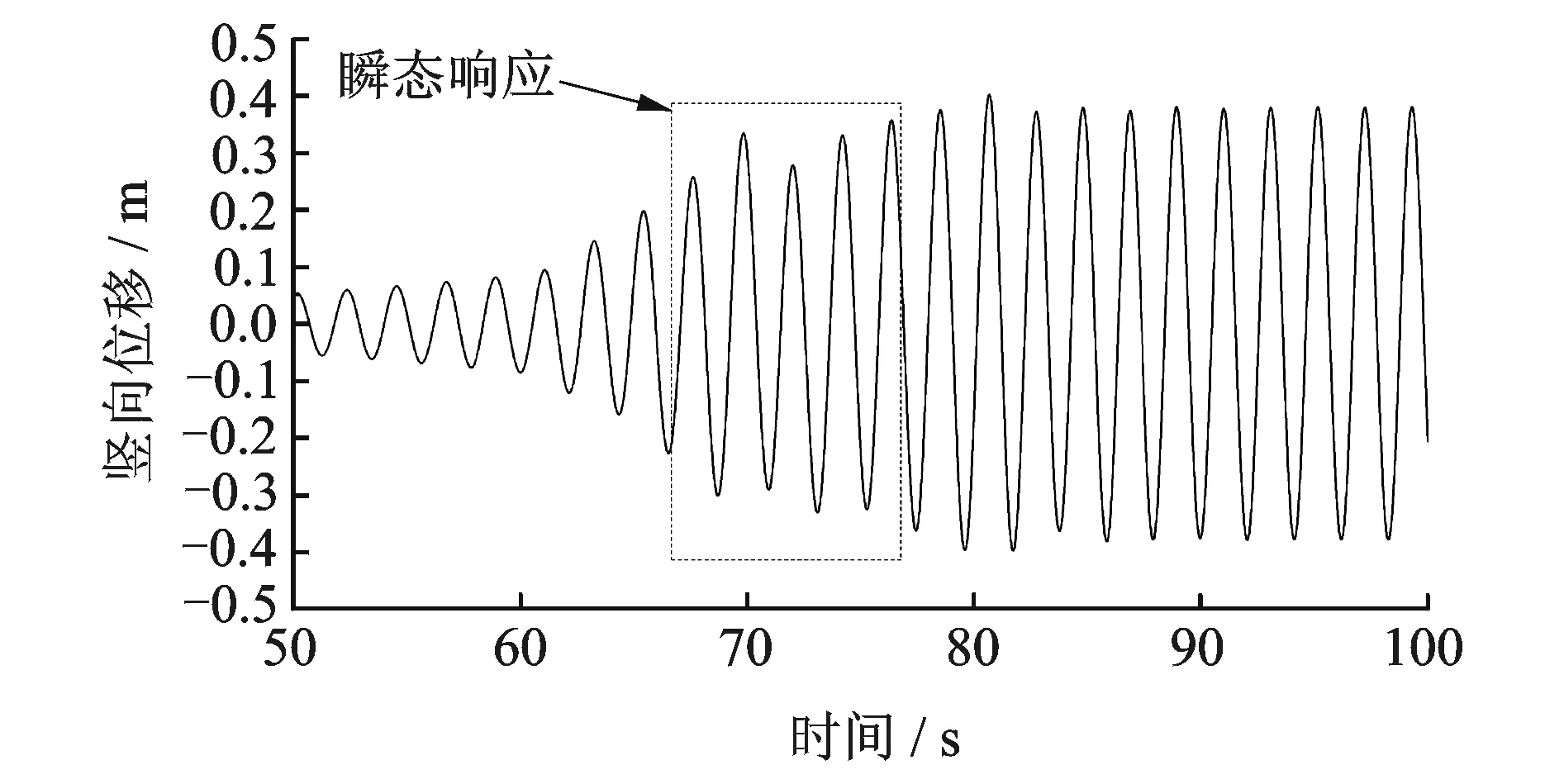
图1 不同阶段阶跃函数之间突然切换时引起的非物理的瞬态响应Fig.1 Non-physical transient responses induced by sudden switching to a new group of indicial functions

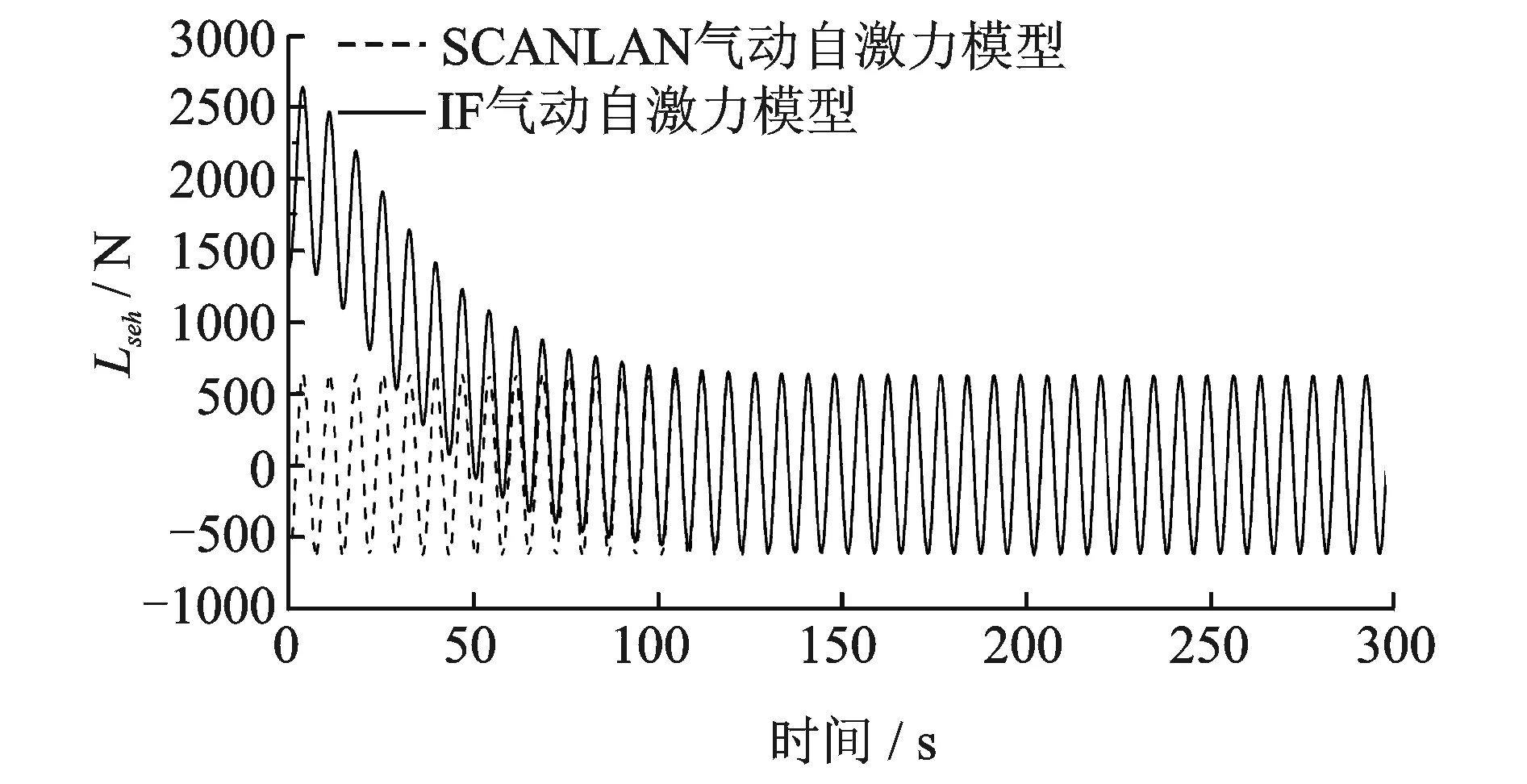
图2 单位正弦竖向运动引起的自激升力LsehFig.2 An example of lift Lseh due to unit sinusoidal vertical motion

为了避免上述可能出现的非物理瞬态响应，本文引入平行激励的求解策略，具体思路如下：对于时域分析的任意时刻，同时采用所有阶段的阶跃函数分别独立地计算它们对应的每个断面的自激力作为备用；然后根据公式(12)确定每个断面所处的中间振幅状态；最后，每个断面的自激力可通过对某相邻的两组自激力进行线性插值确定，如公式(17)与(18)所示。这种平滑处理的方法成功地消除了非物理的瞬态响应现象。图3直观地展示了此求解思路的具体过程。

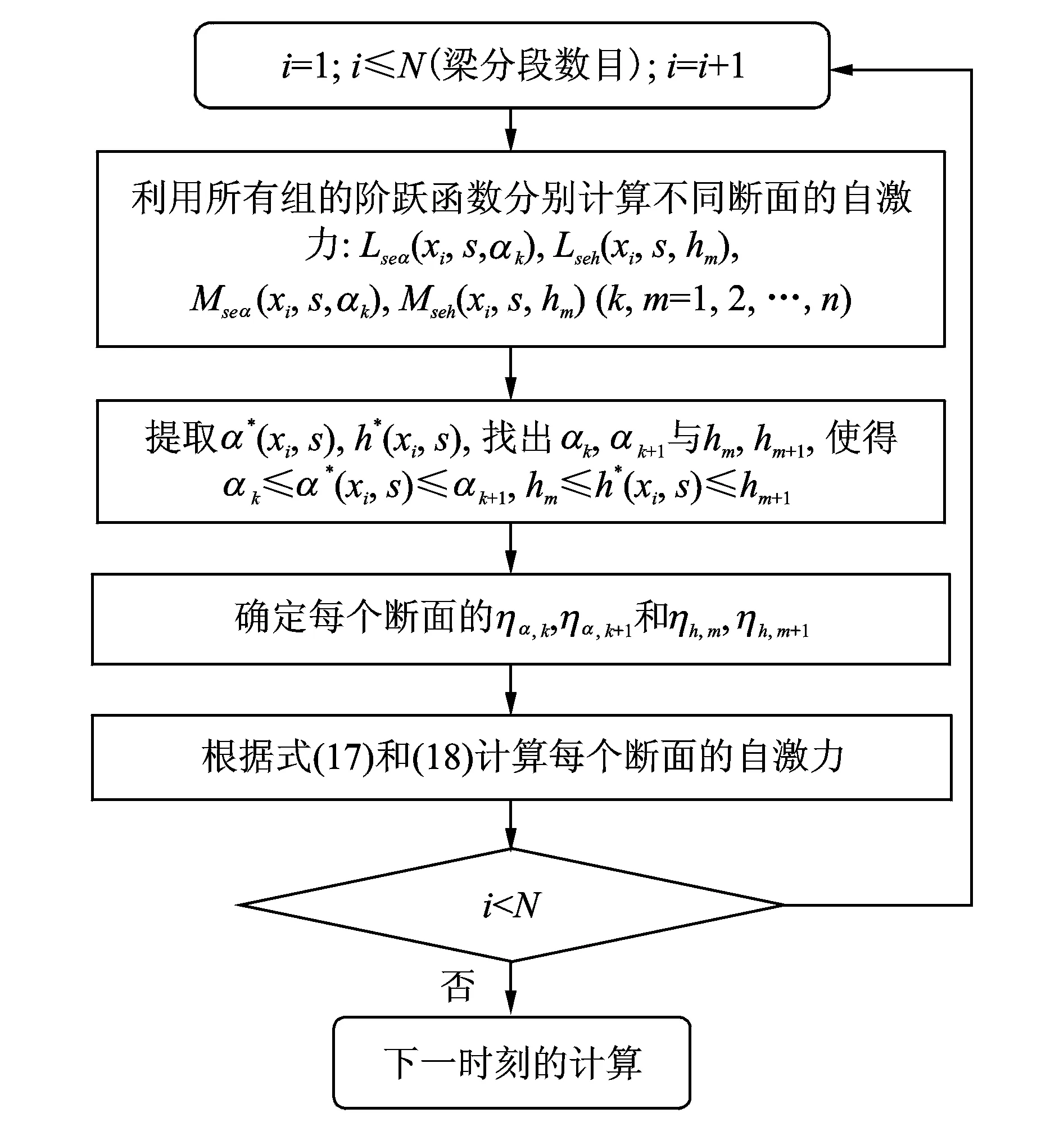
图3 采用多阶段阶跃函数确定各断面的非线性气动自激力的流程图Fig.3 Flow chart for determination of nonlinear aerodynamic self-excited loads by multi-stage indicial functions

3 气动力的一体化与兼容性

3.1 平均风荷载

一般地，单位长度主梁的平均阻力、升力与升力矩采用静力三分力系数来表达：

(19)

(20)

(21)

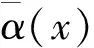
(22)

平均风荷载是风攻角的非线性函数。借助泰勒展开式将三分力在初始风攻角位置展开成如下表达式：

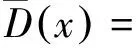
(23)

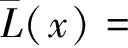
(24)

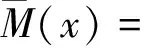
(25)

3.2 时域气动自激力的平均特性

若结构处于一个稳态的随机振动过程，它的总响应可以写成平均响应与脉动响应两部分之和：

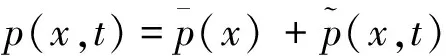
(26)

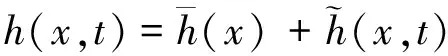
(27)

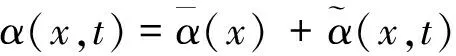
(28)

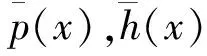
IF气动自激力模型的平均值可通过对公式(5)和(6)所示的自激力时域表达式求数学期望获得，过程如下：

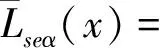
(29)

(30)

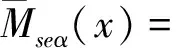
(31)

(32)

式中 E表示求数学期望。上述的4个数学期望具有明显的物理意义，它们分别代表平均扭转响应与平均竖向响应引起的气动自激力部分。由公式(29)至(32)发现，IF自激力模型平均值正好与公式(24)与(25)等号右边的第二项即断面扭转引起的平均风荷载的一阶项完全相等。因此，在时域分析中，当平均风荷载与气动自激力同时考虑时，就会出现部分风荷载的重复计算。下节将引入伪稳态自激力分离法解决这一问题。

3.3 伪稳态自激力分离法

由于IF自激力模型不能反映平均风荷载的非线性特性，因此可从IF自激力模型中扣除其平均值来解决了部分气动力被重复考虑的问题，再单独处理平均风荷载的非线性，即利用公式(19)～(21)逐步计算平均风荷载，且在每一时间步，根据断面扭转角来修正其值[25]。

然而从IF自激力模型中扣除其平均值面临两大困难：一方面，结构的平均响应事先未知；另一方面，即便结构的平均响应已知，但从自激力模型中突然扣除结构平均响应引起的气动力将会导致强烈的瞬态响应。鉴此，本文引入伪稳态响应的概念，定义如下：

(33)

(34)

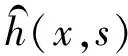
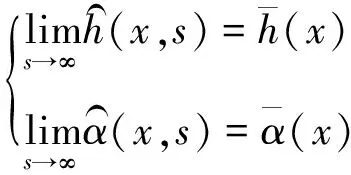
(35)

由此可见，伪稳态响应随着时间的推移最终收敛于结构的平均稳态响应。

根据其极限特性，可以得到如下等式：

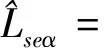
(36)

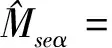
(37)

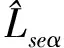
(38)

(39)

式中

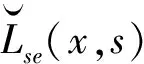
(40)

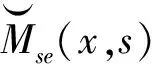
(41)

其中

(42)

式中Lb(x,s)与Mb(x,s)分别为随时间变化的抖振升力与升力矩，其表达式如下：

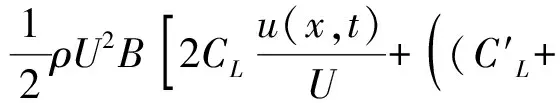
(43)

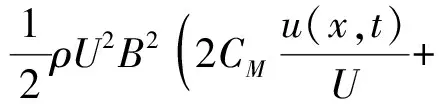
(44)

式中u(x,t)与w(x,t)分别为顺风向与竖风向脉动风速。公式(40)与(41)右边的第三项即为扣除的伪稳态气动自激力。需要说明的是，本文暂不考虑抖振力的作用。

为了验证伪稳态自激力分离法的可行性与正确性，以某大跨悬索桥为例，采用三种荷载模式来考察主梁中点的阶跃响应。三种荷载工况具体描述如表1所示，其中模式M2与模式M3的唯一差异在于后者从IF自激力模型中扣除了伪稳态自激力而前者未扣除。

表1 荷载模式描述

需要强调的是，无论气弹效应考虑与否，结构的阶跃响应都应该逐渐收敛于一个相同的稳态值。换言之，气弹效应不会对结构最终的静力平衡位置或者平均结构响应产生任何影响。图4给出了三种荷载模式下主梁中点的响应时程。由图可知，荷载模式M1与和荷载模式M3所对应的响应逐渐收敛于真实的静平衡位置，而荷载模式M2最终收敛于一个错误的平衡位置，由此证明了伪稳态自激力分离法可以有效的解决部分气动荷载被重复考虑的问题。

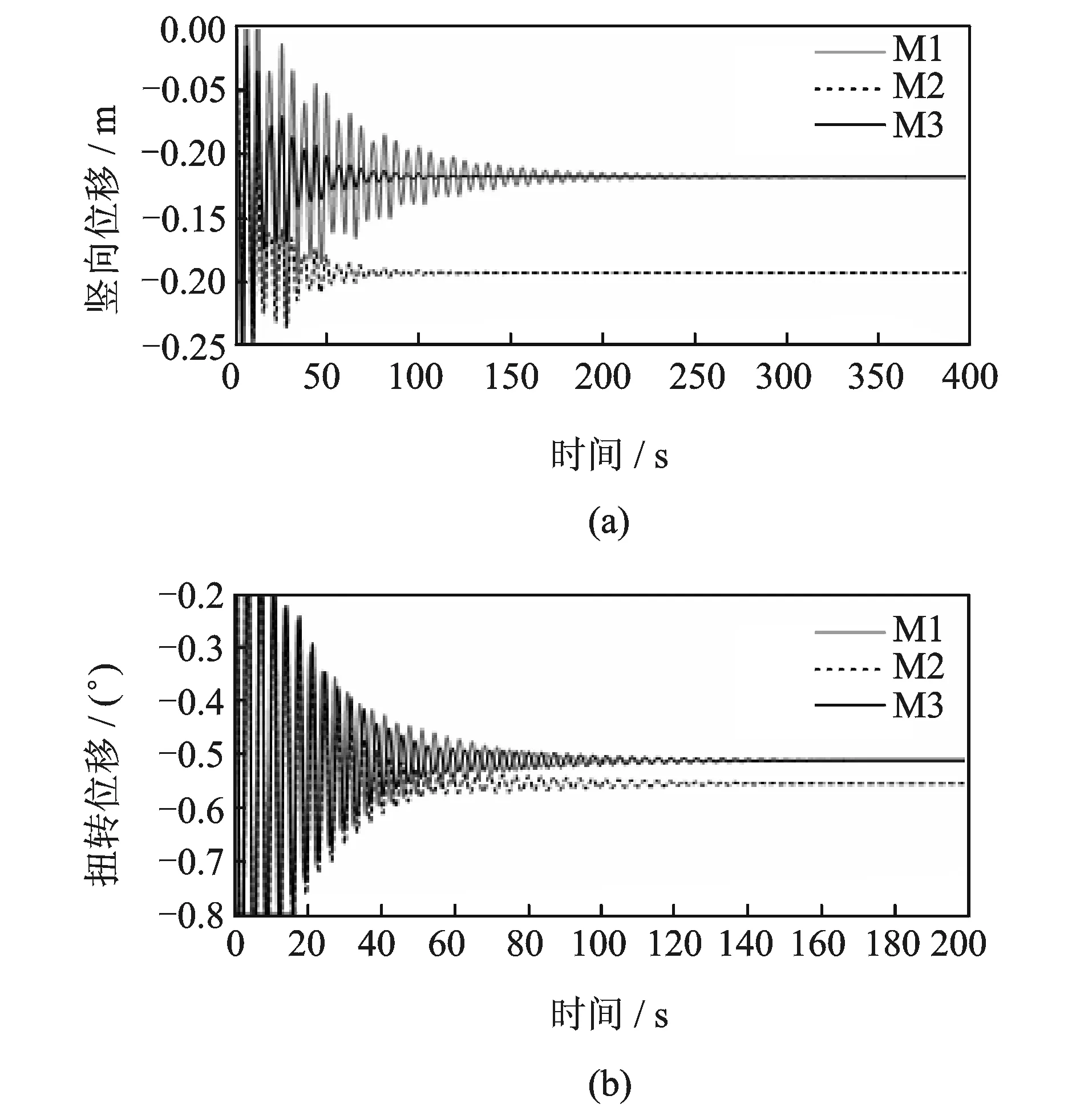
图4 平均风荷载的阶跃响应Fig.4 Step response to mean wind loads

4 数值算例

4.1 有限元模型与气动参数

为了验证本文提出的后颤振时域分析方法与求解策略的可行性，以一薄平板结构为数值算例。模型的参数如下：平板长度为4 m，宽度为0.30 m，每延米的质量和质量惯性矩分别为11.25 kg/m和0.2828 kg·m2/m，模型具有竖向与扭转双自由度。采用ANSYS有限元软件建模，其中平板与横梁采用beam4单元模拟，弹簧支架采用link8单元模拟，质量惯性矩采用mass21单元模拟，有限元模型如图5所示。

颤振导数采用Noda等学者所做的宽厚比B/D等于150的矩形断面的风洞试验成果[26]。基于颤振导数，按照第1节的方法分别识别得到不同阶段振幅状态对应的阶跃函数，拟合参数di(i=1～3)的取值范围设定为区间(0,2.1]。表2给出了不同振幅对应的阶跃函数参数值，图6则为根据阶跃函数反算的颤振导数值。

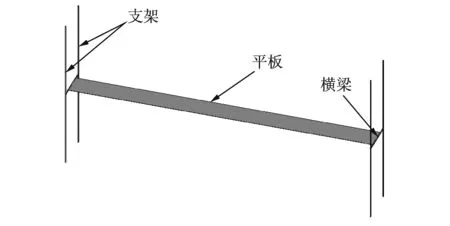
图5 薄平板有限元模型Fig.5 FE model of a thin plate

在颤振时域分析中，结构的阻尼效应采用瑞利阻尼模型模拟，即将结构的阻尼矩阵表达成质量矩阵与刚度矩阵的线性组合，其表达式为

C=aM+bK

(45)

式中C，M与K分别为结构的阻尼矩阵、质量矩阵与刚度矩阵；a与b分别为瑞利阻尼系数。

因结构变形引起结构刚度改变的一类问题都属于几何非线性问题。已有研究表明风洞试验中的弹性悬挂节段模型体系具有明显的非线性刚度特性[27]。

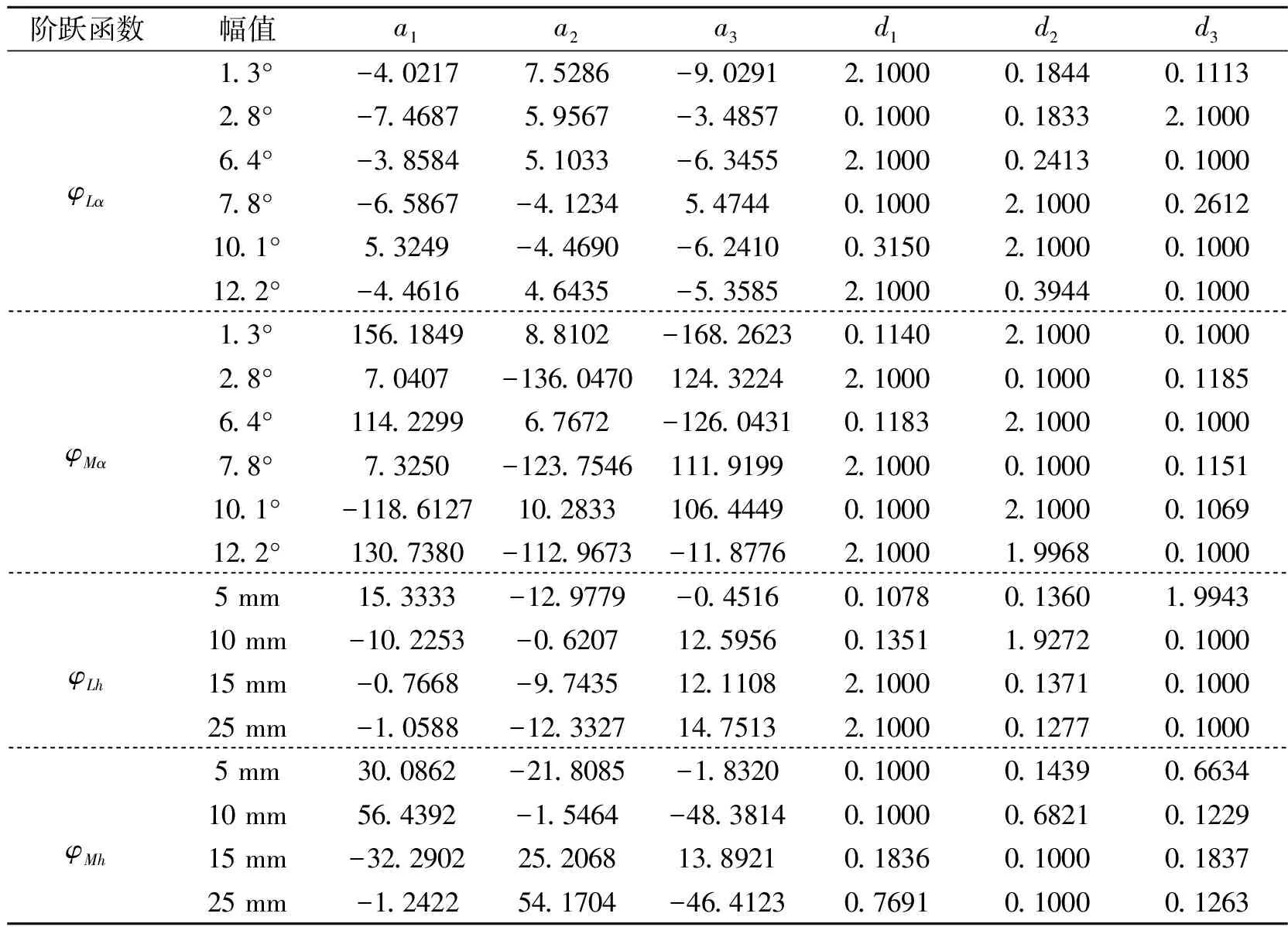
表2 不同振幅对应的阶跃函数参数值

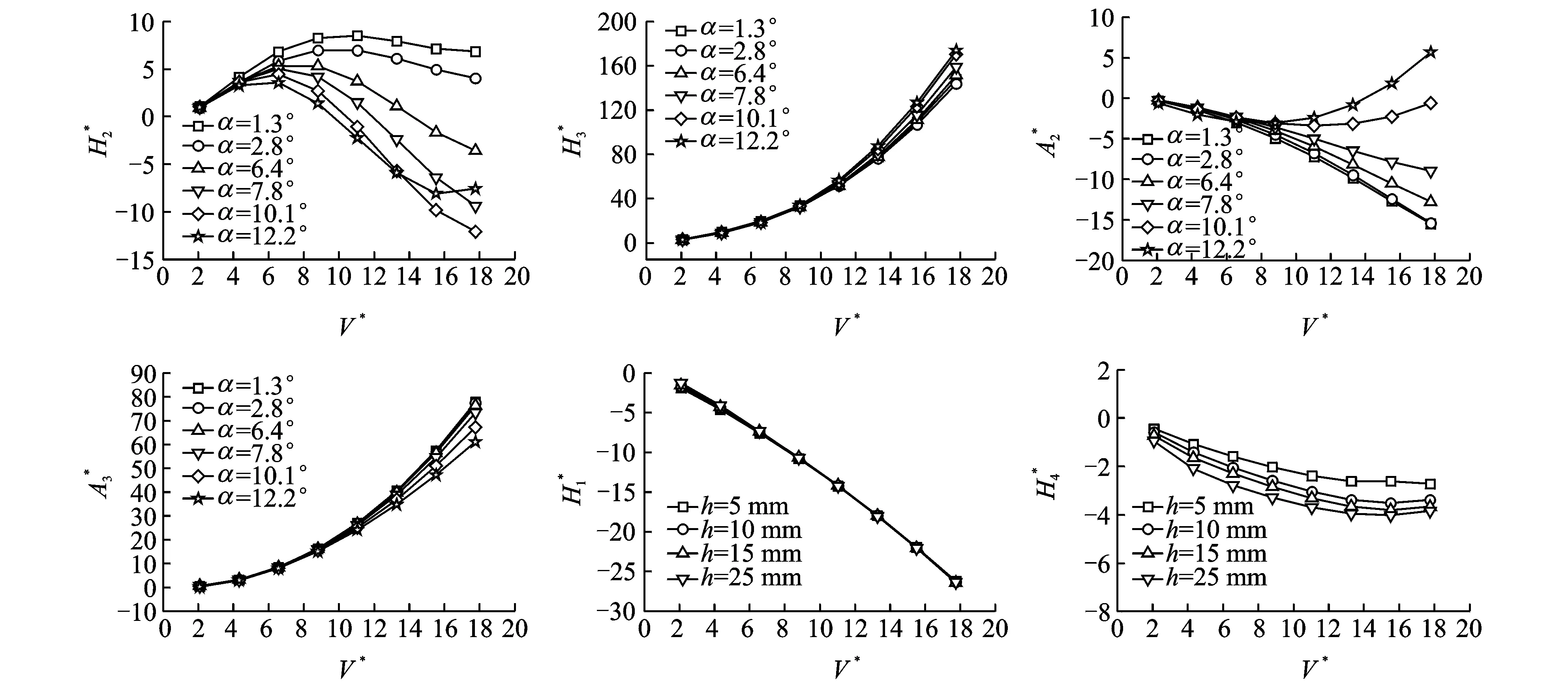
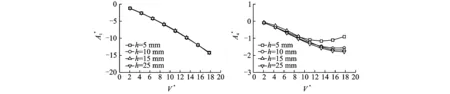
图6 根据识别的阶跃函数反算的颤振导数Fig.6 Flutter derivatives re-obtained from the identified indicial functions

在ANSYS瞬态分析中，可通过打开大变形开关(即设置NLGEOM,ON)来考虑结构的几何非线性效应。表3与4分别列出了颤振时域分析的主要计算参数与工况描述。

表3 颤振时域分析的计算参数

Tab.3 Calculation parameters of flutter time-domain analysis

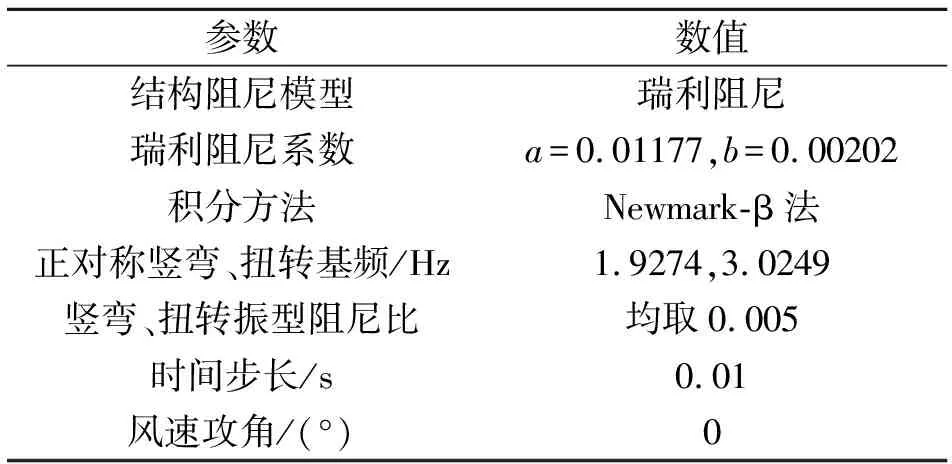
参数数值结构阻尼模型瑞利阻尼瑞利阻尼系数a=0.01177,b=0.00202积分方法Newmark-β法正对称竖弯、扭转基频/Hz1.9274,3.0249 竖弯、扭转振型阻尼比均取0.005时间步长/s0.01 风速攻角/(°)0

表4 时域分析的工况描述

Tab.4 Descriptions of calculation cases of time-domain analysis

工况几何非线性气弹非线性平均风效应L-L-EX不包含不包含不包含N-L-EX包含不包含不包含N-N-EX包含包含不包含N-L-IN包含不包括包含N-N-IN包含包含包含

4.2 颤振时域分析与结果讨论

4.2.1 颤振临界风速

采用ANSYS软件分别求解了表4所列的5种工况对应的平板颤振临界风速值，如图7所示。由此得出两点结论：(1)对比L-L-EX，N-L-EX与N-N-EX三种工况可知，结构的几何非线性几乎不影响线性模型对应的颤振临界风速，然而气弹非线性效应在一定程度上降低了颤振临界风速，这表明在颤振临界状态下，虽然平板振动体系的几何非线性微乎其微，但已呈现出了一定的气弹非线性效应。(2)对比N-L-EX工况与N-L-IN工况可知，在气弹模型中计入平均风效应后，颤振临界风速从7.392 m/s降至6.75 m/s，由此可见，在颤振分析中不考虑平均风荷载将会明显高估结构的颤振稳定性能。因此，一体化考虑平均风效应与气弹效应是颤振及后颤振时域分析的必然趋势。

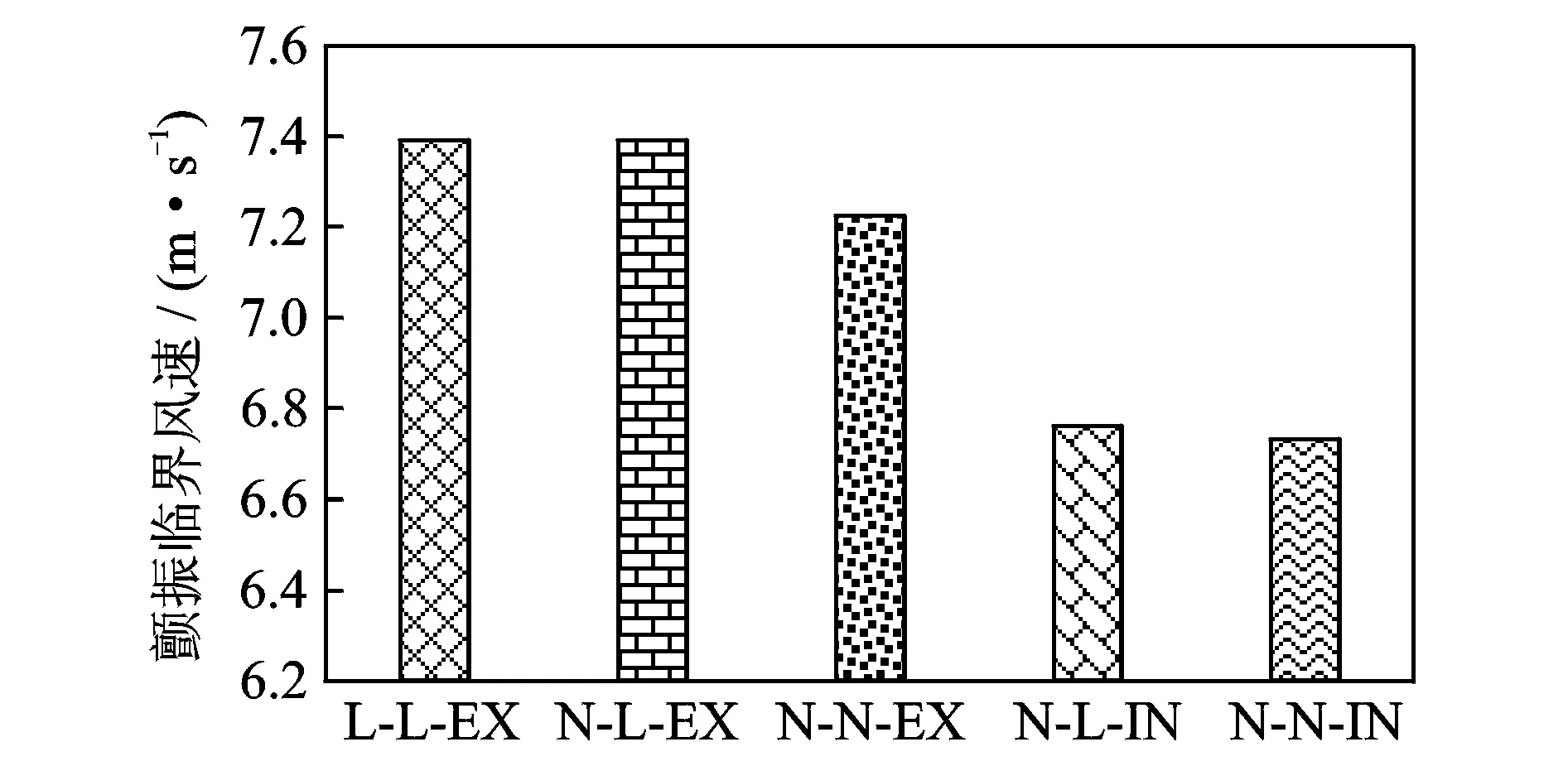
图7 颤振临界风速Fig.7 Critical wind speeds of flutter

4.2.2 后颤振LCO特性

图8给出了5种工况对应的颤振扭转响应时程曲线。由图可得到如下结论：对于线性模型(工况L-L-EX)，当风速超过临界值时，扭转响应呈指数式增长，即线性理论揭示的典型颤振发散现象，如图8(a)所示，这种现象显然是不符合工程实际的；当仅考虑几何非线性时(工况N-L-EX)，后颤振响应最终演变成具有稳定幅值的LCO状态，如图8(b)所示，这与航空领域揭示的平板几何非线性可导致LCO的结论是一致的[6]。当同时考虑几何与气弹非线性时(工况N-N-EX)，后颤振LCO的幅值相比同风速下工况N-L-EX对应的幅值大得多，而且达到LCO状态所需的时间大大缩短，如图8(c)所示，即表明气弹非线性效应可显著地影响后颤振极限环特性(如LCO幅值、演变过程等)。当一体化考虑平均与气弹风效应时(工况N-L-IN与N-N-IN)，平板在较低风速时就呈现了稳定幅值的LCO现象，且LCO的发展速度很快，如图8(d)及(e)所示。图9表明了平板达到LCO状态所需的时间随着风速的增加而减少；此外，在同一风速下，工况N-N-IN所需的时间比工况N-L-IN的有所缩短。

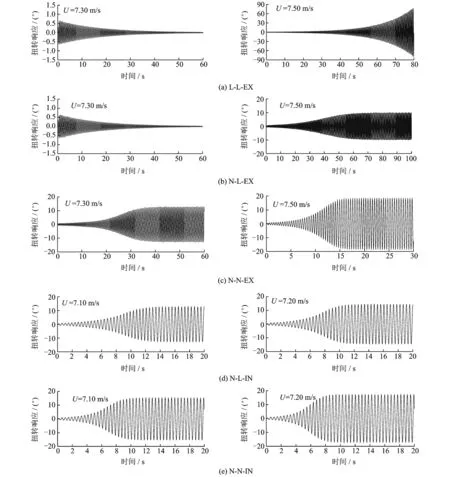
图8 平板的扭转响应时程曲线Fig.8 Time histories of rotation of the plate

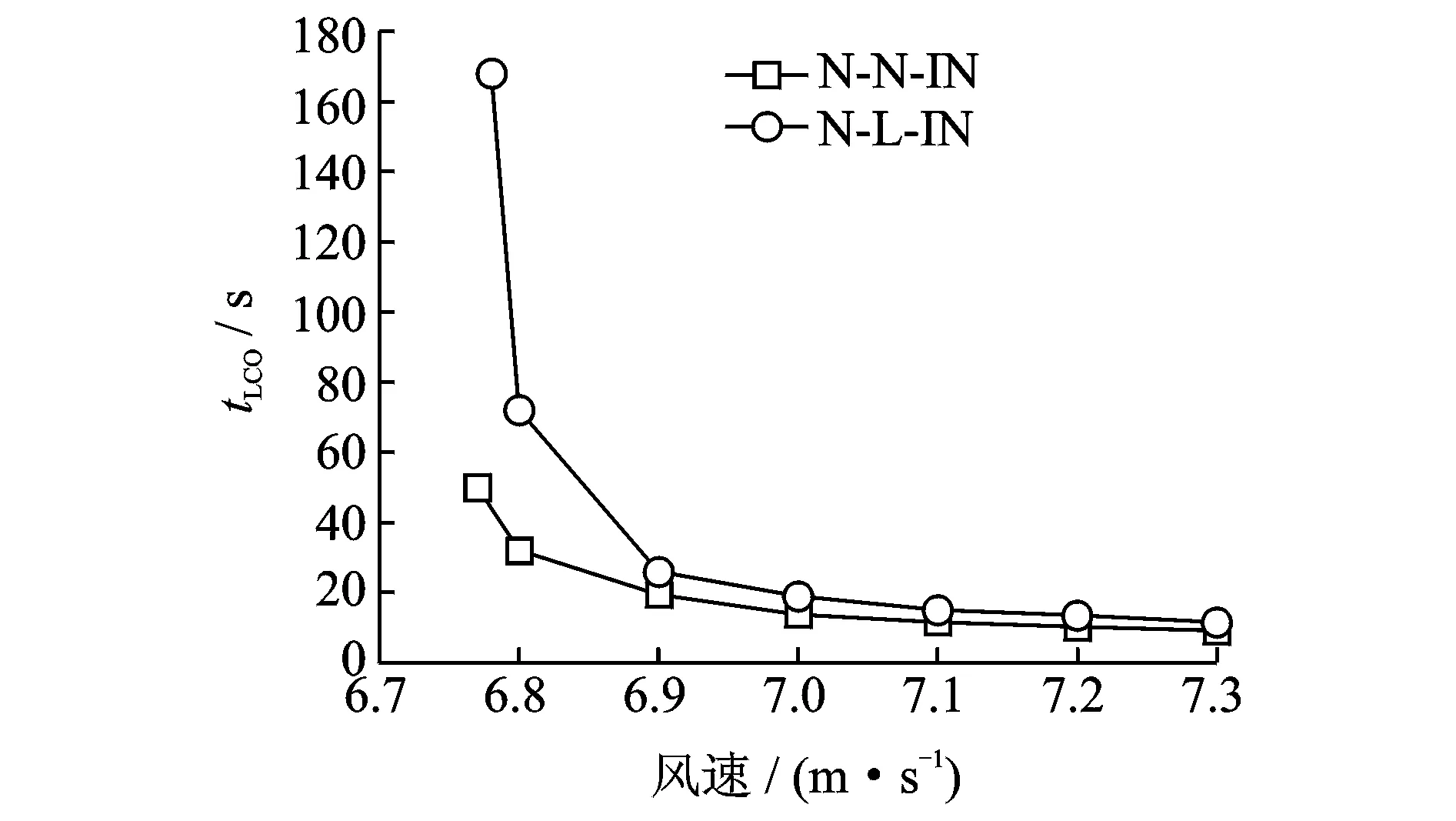
图9 结构达到LCO状态所需的时间Fig.9 The time required for the plate reaching LCO

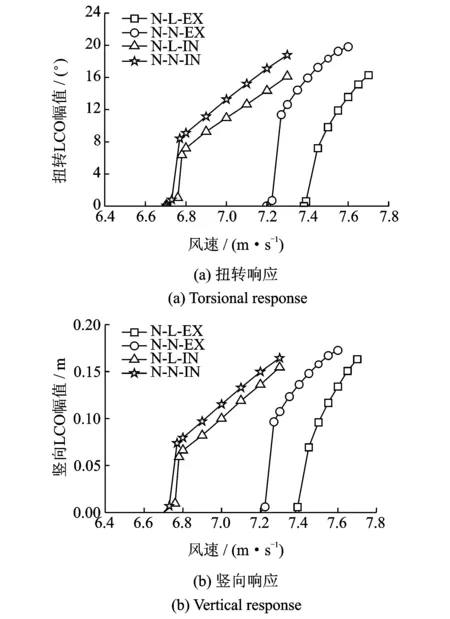
图10 LCO幅值随风速的变化曲线Fig.10 LCO amplitudes versus wind speeds

综上可知，当考虑非线性效应后，结构的后颤振响应表现为稳态的LCO状态，且LCO的幅值与演变规律与振动体系的非线性强弱紧密相关，此外平均风效应可显著地降低结构的颤振临界风速，使结构提前且更为快速地进入后颤振LCO状态。

图10给出了平板的后颤振LCO幅值随风速的变化曲线。由图可知，竖向与扭转LCO的幅值均随着风速的增加而增加,但幅值递增的规律与振动体系的非线性特性及是否考虑平均风效应紧密相关。由图10得出了如下两点结论：(1)在同一风速下，对于同时考虑几何及气弹非线性的情形(如工况N-N-EX或N-N-IN)，其对应的LCO幅值比只考虑几何非线性的情形(如工况N-L-EX或N-L-IN)要大；(2)对于考虑平均风效应的情形(工况N-L-IN与N-N-IN)，虽然颤振临界风速有所降低，然而后颤振LCO幅值随风速的增长速率相比未考虑平均风效应的情形(工况N-L-EX与N-N-EX)要缓一些，且呈现近似线性增长的趋势。

断面的非线性气弹效应与结构的非线性特性决定了后颤振振幅的演变过程与LCO的幅值，因此不同的气动外形与结构体系，其表现的后颤振性能也不同。结构的后颤振LCO幅值确定后，可以得到各构件的内力与应力幅值，再结合材料非线性及疲劳特性，可判断各构件是否出现强度破坏或者达到疲劳破坏的振动持续时间，从而找到结构在后颤振过程中的薄弱环节，为从设计角度上提高结构的抗风强健性提供依据。

5 结 论

本文实现了一体化考虑平均风与气弹效应的非线性后颤振时域算法，通过理论分析与数值计算，得出以下结论：

(1)多阶段阶跃函数(Multi-stage IFs)可以描述结构断面的气弹非线性特性。通过对离散的多阶段阶跃函数进行线性插值可以模拟连续的幅值相关的非线性气弹特性。

(2)采用伪稳态自激力分离法从IF气动自激力模型中扣除了平均扭转响应引起的自激力部分，解决了一体化考虑平均风荷载与气动自激力所引起的部分气动力被重复计入的问题，同时也保留了平均风荷载的非线性特性。

(3)数值计算表明，后颤振LCO特性与振动体系的非线性特性密切相关。与只考虑几何非线性的情形相比，气弹非线性显著地改变了后颤振幅值演变过程与LCO的幅值；此外，在颤振分析中，平均风荷载的计入明显地降低了结构的颤振临界风速值，也显著地改变了结构的后颤振LCO特性。

(4)与线性理论揭示的颤振发散相比，非线性分析揭示的后颤振LCO幅值受限，可以通过选取良好的气动外形来降低结构的LCO的幅值以及提高结构的抗疲劳性能，从而增强结构的强健性，以此来保证结构在有限的振动时间内不发生致命的破坏。

本文为大跨度桥梁结构的非线性后颤振分析提供了理论基础与求解思路。如果桥梁断面在一系列由小到大的离散振幅下的颤振导数均得到了，那么可采取本文方法进行后颤振分析，确定其后颤振极限环特性，并可进一步考虑结构的材料非线性、疲劳特性以及构件的薄弱环节等强健性因素来评估LCO状态下桥梁结构的稳定性和安全性。

[1] Dowell E H. A Modern Course in Aero-elasticity[M]. Fifth Revised and Enlarged Edition: Dordrecht: Springer International Publishers, 2015.

[2] Feistauer M, Horacek J, Ruzicka M, et al. Numerical analysis of flow-induced nonlinear vibrations of an airfoil with three degrees of freedom[J]. Computers & Fluids, 2011,49(1):110—127.

[3] Wang S, Ingham D B, Ma L, et al. Turbulence modeling of deep dynamic stall at relatively low Reynolds number[J]. Journal of Fluids and Structures, 2012,33:191—209.

[4] Gharali K, Johnson D A. Dynamic stall simulation of a pitching airfoil under unsteady freestream velocity[J]. Journal of Fluids and Structures, 2013,42:228—244.

[5] Tran C T, Petot D. Semi-empirical model for the dynamic stall of airfoils in view of the application to the calculation of responses of a helicopter blade in forward flight[J]. Journal of Vertica, 1981,5(1):35—53.

[6] Tang D M, Dowell E H. Nonlinear aeroelasticity in rotorcraft[J]. Mathematical and Computer Modelling, 1993,18(3-4):157—184.

[7] Sarkar S, Bijl H. Nonlinear aeroelastic behavior of an oscillating airfoil during stall-induced vibration[J]. Journal of Fluids and Structures, 2008,24(6):757—777.

[8] Stanford B, Beran P. Direct flutter and limit cycle computations of highly flexible wings for efficient analysis and optimization[J]. Journal of Fluids and Structures, 2013,36:111—123.

[9] Leishman J G, Beddoes T S. A semi-empirical model for dynamic stall [J]. Journal of the American Helicopter Society, 1986,34(3):3—17.

[10] Larssen J W, Nielsen S R K, Krenk S. Dynamic stall model for wind turbine airfoils[J]. Journal of Fluids and Structures, 2007,23(7):959—982.

[11] Diana G, Rocchi D, Argentini T, et al. Aerodynamic instability of a bridge deck section model: Linear and nonlinear approach to force modeling[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010,98(6-7):363—374.

[12] Wu T, Kareem A. Modeling hysteretic nonlinear behavior of bridge aerodynamics via cellular automata nested neural network [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011,99(4):378—388.

[13] Wu T, Kareem A. A nonlinear analysis framework for bluff-body aerodynamics: a volterra representation of the solution of Navier-Stokes equations[J]. Journal of Fluids and Structures, 2015,54:479—502.

[14] 王 骑, 廖海黎, 李明水, 等. 桥梁断面非线性自激气动力经验模型[J]. 西南交通大学学报，2013,48(2):271—277.

Wang Qi, Liao Haibing, Li Mingshui. Empirical mathematical model for nonlinear motion-induced aerodynamic force of bridge girder[J]. Journal of Southwest Jiaotong University, 48(2):271—277.

[15] 朱乐东，高广中．双边肋桥梁断面软颤振非线性自激力模型[J]．振动与冲击，2016,35(21):29—35.

Zhu Ledong, Gao Guangzhong. A nonlinear self-excited force model for soft flutter phenomenon of a twin-side-girder bridge section[J]. Journal of Vibration and Shock,2016,35(21):29—35.

[16] Zhang M J, Xu F Y, Ying X Y. Experimental investigation on soft flutter of a bridge deck[C]. Proceeding of ACEM 16, Jeju, Korea, 2016:1—22.

[17] 刘十一，葛耀君. 非线性子系统的大振幅时域自激力模型[J].哈尔滨工业大学学报，2015,47(9):73—79.

Liu Shiyi,Ge Yaojun. Nonlinear dynamic subsystem model for large-amplitude motion-induced aerodynamic forces of bridge decks[J]. Journal of Harbin Institute of Technology, 2015,47(9):73—79.

[18] Arena A, Lacarbonara W, Valentine D T, et al. Aeroelastic behavior of long-span suspension bridges under arbitrary wind profiles[J]. Journal of Fluids and Structures, 2014,50:105—119.

[19] Zasso A, Stoyanoff S, Diana G, et al. Validation analyses of integrated procedures for evaluation of stability, buffeting response and wind loads on the Messina Bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013,122:50—59.

[20] Chen X, Kareem A. Nonlinear response analysis of long-span bridges under turbulent winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001,89(14-15):1335—1350.

[21] Chen X, Kareem A. Aeroelastic analysis of bridges: effects of turbulence and aerodynamic nonlinearities[J]. Journal of Engineering Mechanics, 2003,129(8):885—895.

[22] Scanlan R H. Problematics in formulation of wind-force models for bridge decks [J]. Journal of Engineering Mechanics, 1993,119(7):1353—1375.

[23] Scanlan R H. Motion-related body force functions in two-dimensional low-speed flow [J]. Journal of Fluids and Structures, 2000,14(1):49—63.

[24] Zhang Z T, Chen Z Q, Cai Y Y, et al. Indicial functions for bridge aero-elastic forces and time-domain flutter analysis[J]. ASCE Journal of Bridge Engineering, 2011,16(4):546—557.

[25] 吴长青，张志田.悬索桥的静风扭转发散有限元精细化分析[J]. 湖南大学学报(自然科学版)，2016，43(9):88—97.

Wu Changqing，Zhang Zhitian. Refined analysis of finite element for torsional divergence of suspension bridges[J]. Journal of Hunan University (Natural sciences)，2016，43(9):79—88.

[26] Noda M, Utsunomiya H, Nagao F, et al. Effects of oscillation amplitude on aerodynamic derivatives [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003,91(1-2):101—111.

[27] Gao G Z, Zhu L D. Nonlinearity of mechanical damping and stiffness of a spring-suspended sectional model system for wind tunnel tests[J]. Journal of Sound and Vibration, 2015,355:369—391.