基于压重块型TMD的大跨度斜拉桥减震控制
2018-07-05邹仲钦茅建校陶天友
王 浩, 邹仲钦, 茅建校, 陶天友
(东南大学混凝土及预应力混凝土结构教育部重点实验室, 江苏 南京 210096)
引 言
随着中国经济水平的提高,交通事业也蓬勃发展,近年来兴建了一系列跨江、跨海的大跨度桥梁,如润扬大桥、苏通大桥、杭州湾大桥等[1]。目前,世界上已有不少大跨度桥梁遭受地震破坏的实例[2],如1995年日本神户大桥在神户地震中遭受破坏、1989年旧金山奥克兰湾大桥东跨的悬臂桁架在洛马·普雷塔大地震中倒塌;1999年集集大桥主梁和主塔在集集大地震中破坏等。大跨度桥梁作为重要的生命线工程,如何保证其抗震安全性显然十分重要,而如何对其地震响应进行有效控制也一直是桥梁工程界研究的热点问题之一[2]。
在桥梁结构减震控制方法及控制装置方面,近年来已取得了一系列富有成效的研究成果。而在众多可供选择的控制装置中,质量阻尼器(例如TMD和ATMD)是最常用的装置[3]。TMD是由一个质量块、弹簧和阻尼器组成的系统,可以持续提供一种与主结构运动方向相反的惯性力,以减小结构的动力响应。国内外有许多高耸结构安装了TMD来控制结构的振动,例如,中国台北的101大楼在87~92层间设置了球形质量块并辅以8对油压阻尼器,使减震效果达到了40%[4];美国芝加哥的凯越酒店,采用了质量块为300 t的TMD系统来减少结构的振动响应[5]。在桥梁工程中,中国九江长江大桥使用了TMD系统来抑制吊杆的涡振[6];徐刚等[7]研究了TMD系统对施工中大桥桥塔的减振性能影响;樊健生等[8]研究了人行桥的TMD减振优化设计。但由于TMD的设置将显著增大桥梁结构的恒载,使其在实际工程中的应用受到限制[9]。
对于边主跨比相对较小的斜拉桥,常常通过在边跨设置压重块来平衡主跨重力,若将此类斜拉桥的压重块与钢箱梁间采用弹簧和阻尼装置连接,改装成为压重块型TMD,则可在保持压重块功能的同时,既不增大结构的恒载,又发挥TMD的结构减振功能[10]。为此,本文参照苏通大桥结构,分别建立了有/无辅助墩的两种大跨度斜拉桥的有限元模型,对比分析了大跨桥梁在地震动作用下的结构响应,再将边跨的压重块等效为TMD中的质量块,设计改装成压重块型TMD,并将采用压重块型TMD前后大跨度斜拉桥的地震响应进行了对比分析,为今后大跨度斜拉桥的减震控制研究提供了新思路,同时为未来大跨度斜拉桥压重块型TMD的设计与改装提供了参考。
1 大跨度斜拉桥压重块型TMD设计
苏通大桥为双索面钢箱梁斜拉桥,采用扁平流线型闭口钢箱梁,中心处梁高4 m,含风嘴在内宽41 m,索塔总高为300.4 m,最长斜拉索长度为577 m,全桥共272根斜拉索,塔柱为单箱单室倒Y形截面,为了平衡主跨的自重以减小主塔的纵向弯曲和主跨下挠,在两个边跨分别安装有铁块作为压重块[11]。本节通过对压重块进行全新改装,据此设计出一种新型的压重块型TMD,以在确保压重功能的同时,起到减小结构的地震响应的作用。
1.1 结构有限元模型的建立
本文以苏通大桥为结构原型,设计了两座跨径分别为(100+100+300+1088+300+100+100) m和(500+1088+500) m的大跨度斜拉桥(如表1所示),两桥的主要区别在于边跨是否设有辅助墩。基于ANSYS建立了两种桥型的有限元模型,如图1所示。在该空间模型中,将横梁、加劲梁、索塔和桥墩简化为梁单元,用Beam4单元模拟,其中按斜拉索的吊点进行加劲梁的离散;将斜拉索简化成索单元,用Link10单元模拟,拉索的自重垂度效应采用Ernst方法修正弹性模量来考虑[12],同时斜拉索轴力对刚度的影响采用应力刚化方法添加几何刚度矩阵来考虑[13]。耦合主梁与主塔在横桥向及绕顺桥向的转动自由度,以及主梁与桥墩在竖向和横向自由度,并将桥墩和主塔底部完全固结,不考虑土-桩-结构相互作用。

表1 两种桥型的结构形式对比
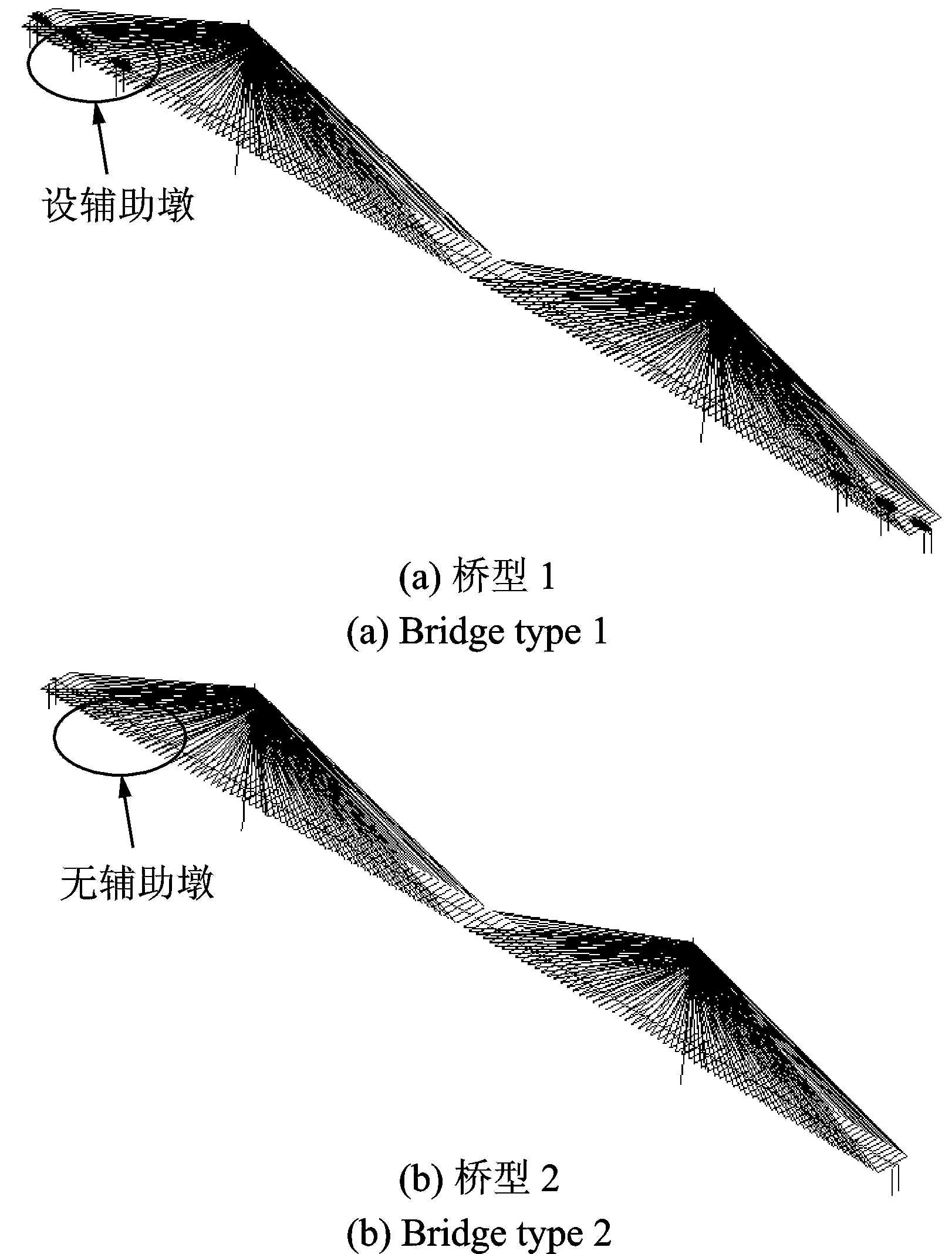
图1 大跨度斜拉桥空间有限元计算模型
Fig.1 Finite element model of the long-span cable-stayed bridges
1.2 压重块型TMD的改装设计
TMD是由一个质量块、弹簧和阻尼器组成的系统。将它与主结构相连并进行适当的调整,由于通过弹簧的连接,可以持续提供一种和主结构的运动方向相反的惯性力,以减小结构的动力响应。本课题组在前期工作中已对压重块型TMD用于钢箱梁风振控制的效果进行了分析[10],并已获得了相应的国家发明专利授权(专利号:ZL 201110197020.9),研究结果表明,压重块型TMD可明显改善大跨度斜拉桥的抖振响应。
大跨度斜拉桥带有压重块的钢箱梁典型截面如图2(a)所示,压重块直接安装在大跨度斜拉桥的钢箱梁底板上。显然可以将压重块等效为质量块,用弹簧和阻尼器和上下连接板相连、用横向限位装置与隔板相连,并采用高强螺栓与桥面连接,形成一个等效的TMD系统,其质量块可以在平面内与钢箱梁产生竖向相对位移,而不产生横向相对位移,如图2(b)所示。其中等效质量块应对称分布在钢箱梁中心线两侧,远离对称轴放置,以增强对大桥侧弯和扭转振动的控制效果。

图2 大跨度斜拉桥的横截面形式
Fig.2 The cross-sections of steel box girder of the long-span cable-stayed bridges
通过ANSYS中的Mass21单元将质量块简化为独立的质量,沿纵轴线对称布置。弹簧和阻尼器均采用ANSYS的Combin14单元来模拟。
2 大跨度斜拉桥地震响应分析
2.1 动力特性分析
采用子空间迭代法分别计算了两种桥型的前300阶模态频率和振型。其中两种桥型的前10阶模态频率和振型对比如表2所示,图3为桥型1的一些典型的振型。
表2 大跨度斜拉桥前10阶模态
Tab.2 The first ten modes and frequencies of the long-span cable-stayed bridges

阶次桥型1桥型2频率/Hz振型描述频率/Hz振型描述10.06384纵飘0.05755纵飘20.10671一阶对称侧弯0.09962一阶对称侧弯30.19100一阶对称竖弯0.11086一阶对称竖弯40.23406一阶反对称竖弯0.14764一阶反对称竖弯50.30463一阶反对称侧弯0.26797一阶反对称侧弯60.33713二阶对称竖弯0.29199二阶对称竖弯70.39297二阶反对称竖弯0.33154二阶对称侧弯80.40232主塔对称侧弯0.33278二阶反对称竖弯90.40807主塔反对称侧弯0.37224三阶对称竖弯100.44504三阶对称竖弯0.37304主塔反对称侧弯
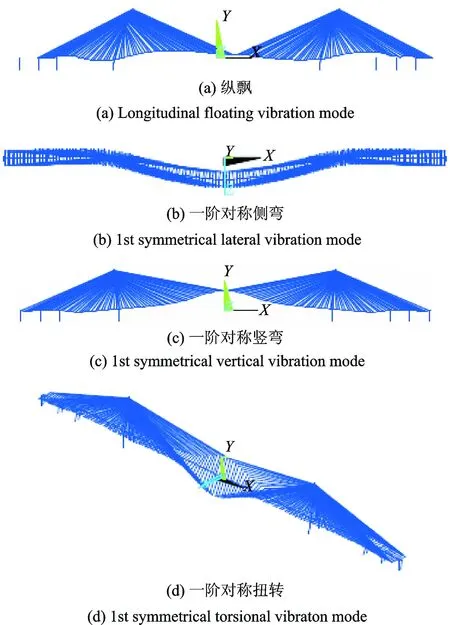
图3 大跨度斜拉桥的一些典型振动模态
Fig.3 Some typical vibration modes of the long-span cable-stayed bridge
表1和图3表明,两种桥型的振型接近,但桥型1的模态频率较桥型2更大,说明辅助墩的存在可以有效提高结构的整体刚度。与桥型2类似,桥型1的第1阶模态的基本周期较长,为15.773 s,对应振型为主梁纵飘,与该桥为漂浮体系相符;第2阶模态频率为0.10671 Hz,对应振型为主梁一阶对称侧弯,第3阶模态频率为0.19100 Hz,对应振型为主梁一阶对称竖弯,该桥的竖弯模态晚于侧弯模态出现,是因为与一般的斜拉桥而相比该桥的宽跨比更小;主塔对称侧弯振型出现在第8阶,其对应的振动频率为0.40232 Hz,主塔反对称侧弯振型出现在第9阶,其对应的振动频率0.40807 Hz,与大跨度斜拉桥自振特性的一般规律相符合[14]。
2.2 地震响应分析
选择常用的Tianjin波、El Centro波和Taft波作为输入的地震动波,并根据《公路桥梁抗震设计细则》[15],将三条波的加速度峰值调整为0.15g,竖向地震波取为相应的水平地震波的1/2。
采用子空间迭代法分别计算两种桥型在三种地震波、分别采用横向、纵向、竖向、横向+竖向和纵向+竖向输入下的地震响应,计算结果表明,两种桥型的响应规律近似,在纵向+竖向地震输入下桥梁结构的响应均最大,该工况下桥型1的关键位置响应结果如表3所示。且由表3可知,结构在Tianjin波下的响应最大,因此本文只选取了Tianjin波进行分析,地震波采取纵向+竖向输入方式。
在Tianjin波纵向+竖向输入下,该桥主要是竖向和纵向模态被激发,故本文主要选取结构的竖向时程响应进行分析。其中设辅助墩桥在主跨跨中、主跨L/4处以及边跨跨中的竖向位移和加速度时程分别如图4(a)~(f)所示。
由图4可知,地震作用下结构整体竖向位移响应并不大,最大振幅也在0.5 m以内,对于主跨为1088 m的斜拉桥而言是可以接受的;但结构竖向加速度响应较大,在主跨L/4处的竖向加速度峰值甚至达到了7.45 m/s2,与桥型1类似,桥型2同样在主跨L/4处的竖向加速度响应也较大,其峰值达到了6.21 m/s2。由于过大的结构振动加速度会严重影响到大桥的行车舒适度和运营安全性, 故本文TMD系统主要以控制主跨L/4处的加速度响应为目标来进行设计。
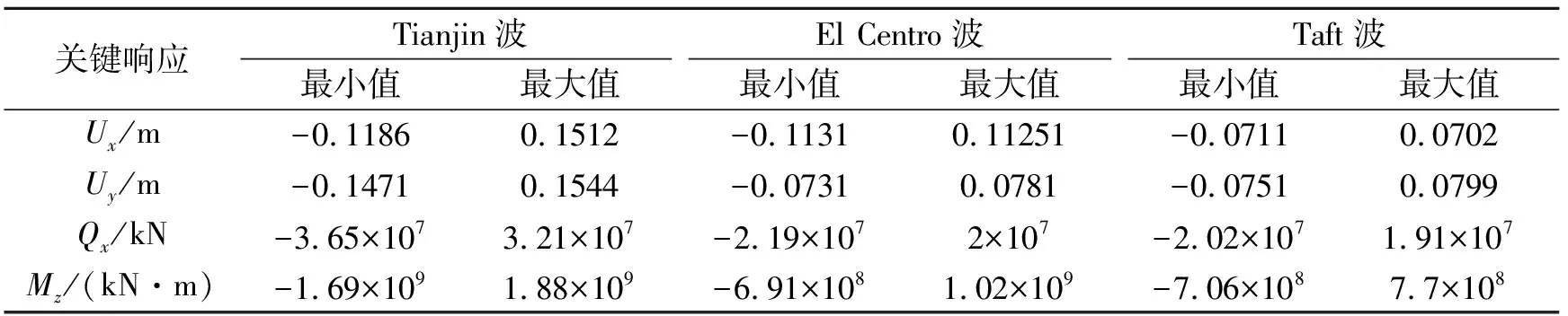
表3 纵向+竖向地震作用下结构关键截面的响应
注:Ux:塔顶纵向位移;Uy:跨中竖向位移;Qx:塔底纵向剪力;Mz:塔底纵向弯矩
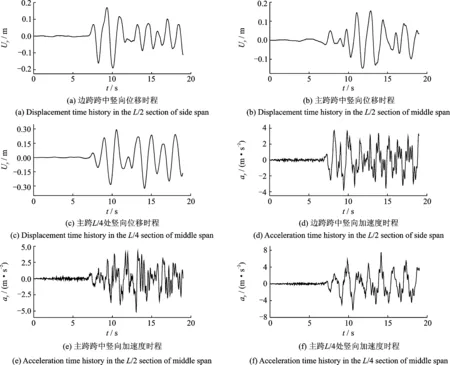
图4 结构关键截面位移及加速度时程Fig.4 Displacement and acceleration time histories of some key sections
3 压重块型TMD减震效果分析
3.1 压重块型TMD参数设计
为了能够实现对主跨L/4处加速度响应的TMD有效控制,首先进行了两种桥型在主跨L/4处的竖向加速度响应的功率谱密度分析,分别如图5(a)和(b)所示。
由图5可知,桥型1的功率谱密度峰值出现在0.659 Hz处,因此根据大桥的动力特性分析结果,考虑控制大桥的第19阶振型,其对应的模态频率为0.654 Hz,与峰值处频率接近;同理,桥型2的功率谱峰值在出现在0.708 Hz处,考虑控制结构的26阶振型。
各桥墩附近所安装的TMD参数如表4所示。表中TMD质量均由相应的压重块质量计算获得,弹簧刚度和阻尼系数通过TMD的参数优化得到。其中桥型1在控制模态下的质量比为0.3088,桥型2对应的质量比为0.122。

表4 TMD的参数
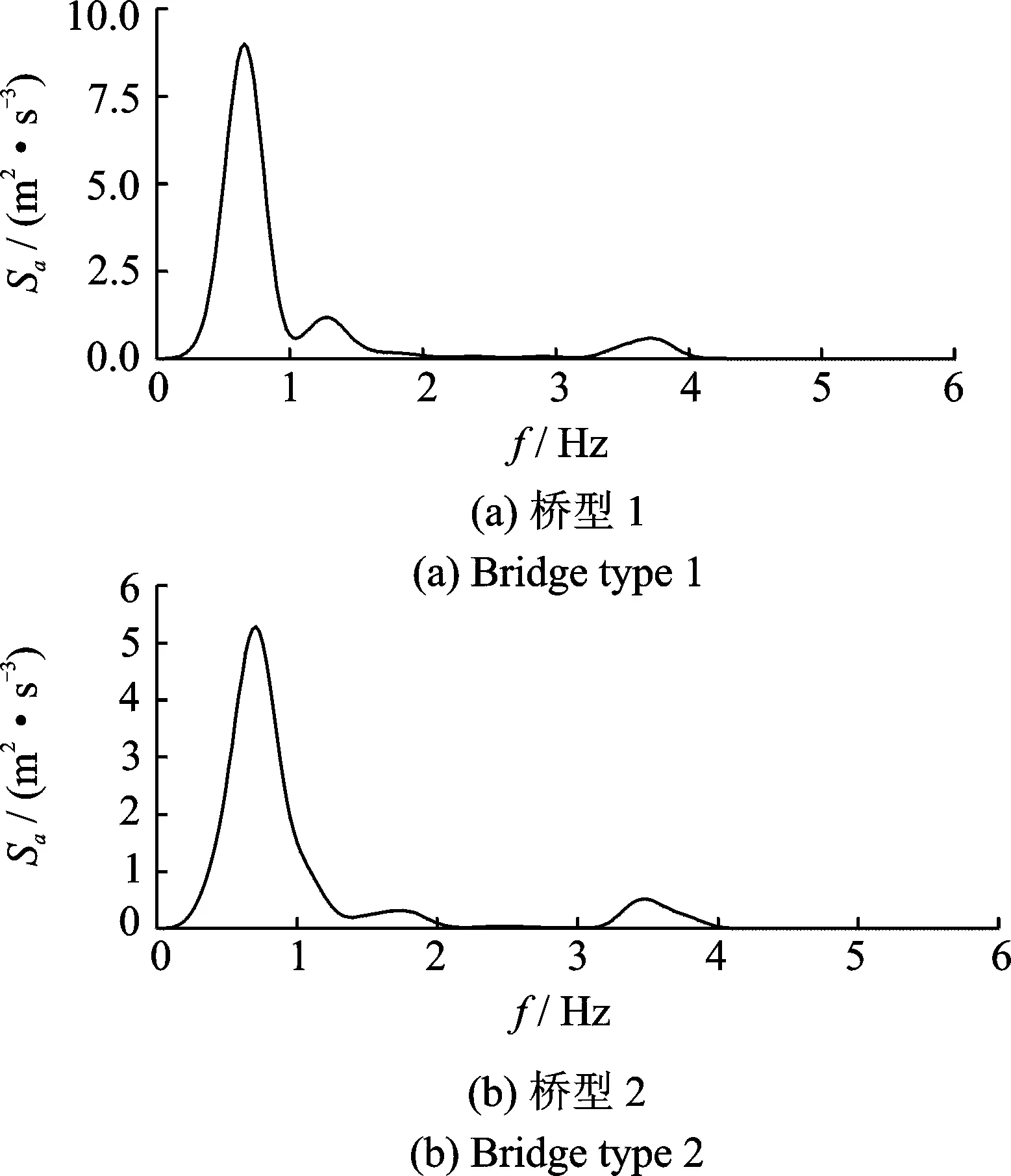
图5 主跨L/4处竖向加速度功率谱密度
Fig.5 Power spectral density of vertical acceleration in the L/4 section of middle span
3.2 TMD减震效果对比分析
采用压重块型TMD前后,桥型1主跨L/4处的竖向加速度时程及其功率谱密度对比分别如图6(a)和(b)所示;采用压重块型TMD前后主跨L/4处的竖向加速度时程及其功率谱密度对比分别如图6(c)和(d)所示。
从图中可知,桥型1采用压重块型TMD后竖向加速度时程峰值为6.06 m/s2,仍然较大。TMD虽然对某些时刻的竖向加速度存在一定的减震效果,但总体而言并没有明显的改善,对功率谱峰值也有一定程度的降低,但并没有达到理想的减震效果;而桥型2采用压重块型TMD后竖向加速度时程峰值为5.30 m/s2,减震率达到21%,由功率谱密度也可知,TMD系统有效降低了功率谱峰值,减震效果明显。原因是当TMD安装在辅助墩附近时,质量块的自由振动会受到限制,因此影响了TMD的减震效果。

图6 采用压重块型TMD前后加速度性能对比
Fig.6 Comparison of acceleration performance of the bridge types with and without TMDs
对于桥型2,即在无辅助墩情况下,压重块型TMD对主梁其他位置依然有很好的控制效果。采用压重块型TMD前后桥型2各位置地震响应峰值对比如表5以及图7~9所示。
表5 采用压重块型TMD前后桥型2各关键截面地震响应峰值对比
Tab.5 Comparison of the peak seismic responses in some key sections of bridge type 2 with and without TMDs
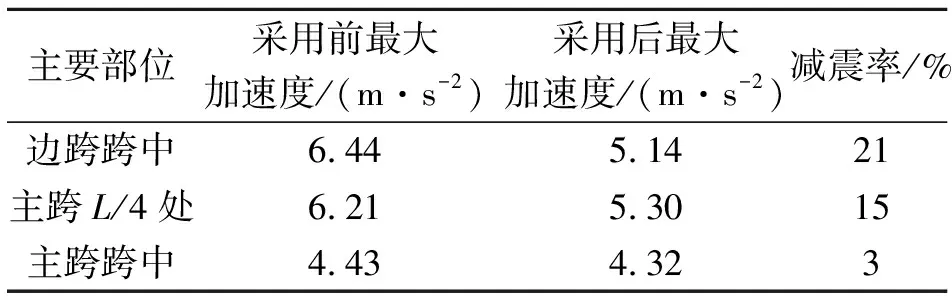
主要部位采用前最大加速度/(m·s-2)采用后最大加速度/(m·s-2)减震率/%边跨跨中6.445.1421主跨L/4处6.215.3015主跨跨中4.434.323
注:减震率定义为采用前后最大加速度差值与采用前最大加速度的比值
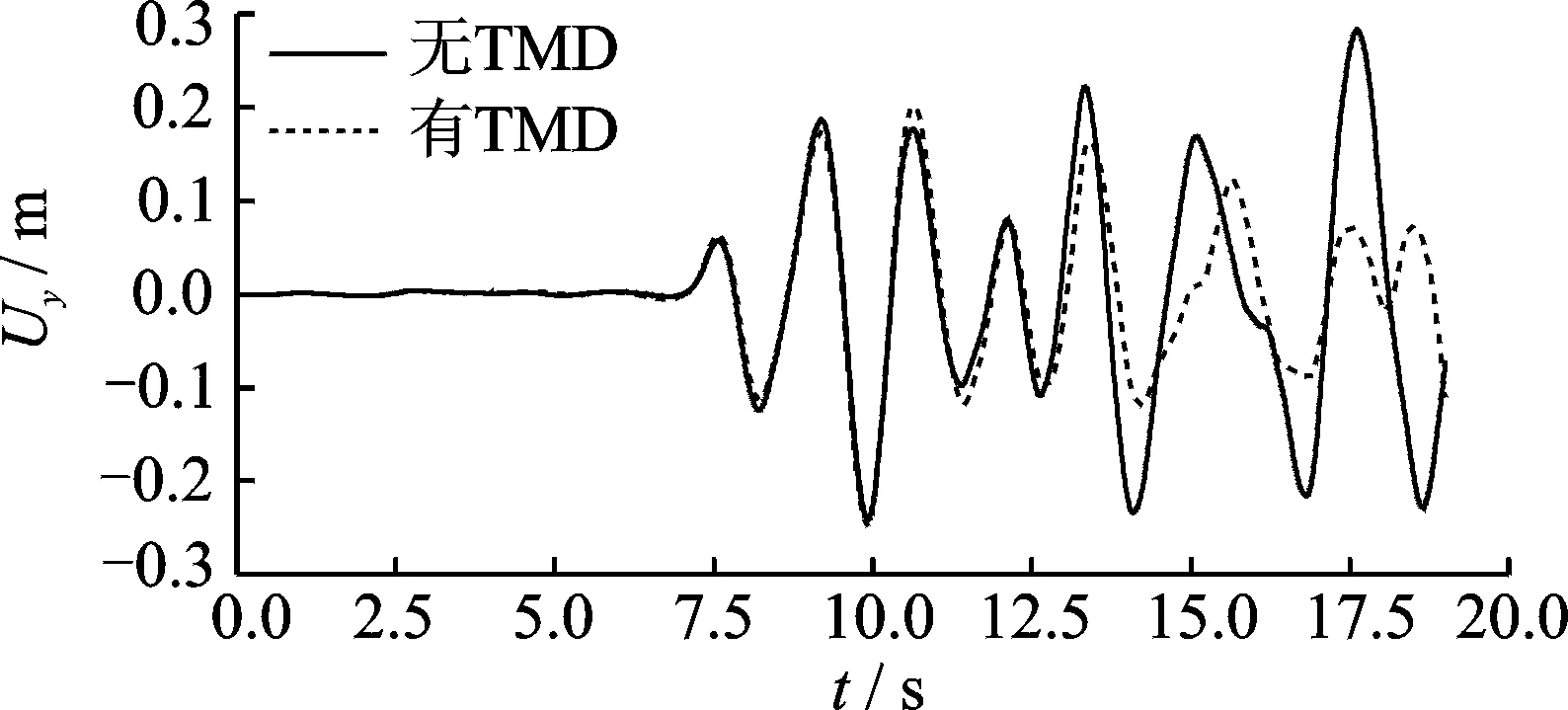
图7 采用压重块型TMD前后主跨L/4处竖向位移时程对比
Fig.7 Comparison of displacement time histories in the L/4 section of the bridge with and without TMDs

图8 采用压重块型TMD前后边跨地震响应对比
Fig.8 Comparison of seismic responses of the side span with and without TMDs
图7为采用压重块型TMD前后主跨L/4处的竖向位移时程对比,可见所设计的压重块型TMD不仅能有效控制主跨L/4处的加速度响应,对该点的位移响应的控制效果同样显著。
图8为采用压重块型TMD前后,该桥边跨跨中竖向加速度时程及其功率谱密度、竖向位移时程对比图。由图8可见,所设计的压重块型TMD对边跨跨中处加速度响应同样有着良好的控制效果。
采用压重块型TMD前后,主跨跨中的竖向加速度时程及其功率谱密度、竖向位移时程对比如图9所示。从图中可知,压重块型TMD对跨中的减震效果不明显,原因是TMD的控制频率对应的结构振型是振型位移为0的反对称竖弯,抑制该阶振型对结构跨中的位移及加速度基本无影响。
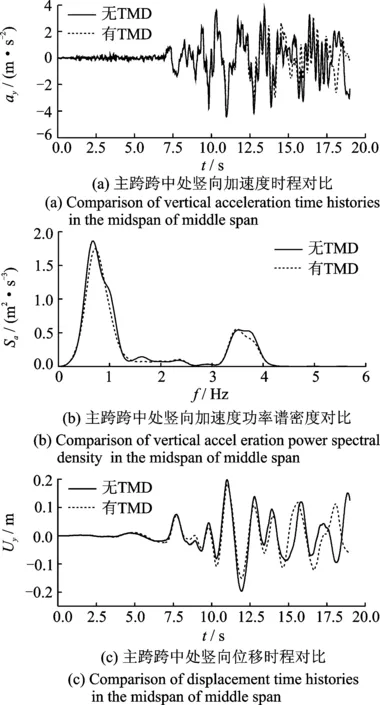
图9 采用压重块型TMD前后主跨地震响应对比
Fig.9 Comparison of seismic responses of the main span with and without TMDs
4 结 论
本文提出了一种基于压重块型TMD的大跨度斜拉桥减震控制方法,所得结论如下:
1) 设计的压重块型TMD能有效控制大跨度斜拉桥的地震响应,在显著减小结构的加速度及位移时程响应的同时,又能保持压重块的功能,减小边主跨比较小产生的主塔弯曲和主跨主梁下挠;
2) 辅助墩的存在一定程度上限制了压重块的运动,影响了TMD的减震效果,因此在辅助墩存在时,压重块型TMD对地震动响应的减震控制效果并不明显;
3) 在无辅助墩时,压重块型TMD对边跨跨中和主跨L/4都有很显著的控制效果,其减震率分别达到了21%和15%,因此在无辅助墩的斜拉桥上采用TMD时能够取得更好的控制效果。
[1] 张喜刚, 刘 高, 马军海. 中国桥梁技术的现状与展望[J]. 科学通报, 2016,(Z1):415—425.
Zhang Xigang, Liu Gao, Ma Junhai. Status and prospect of technical development for bridges in China[J]. Chinese Science Bulletin, 2016,(Z1):415—425.
[2] Siringoringo D M, Fujino Y, Namikawa K. Seismic response analyses of the Yokohama Bay cable-stayed bridge in the 2011 great East Japan earthquake[J]. Journal of Bridge Engineering, 2013, 19(8): A4014006.
[3] 李春祥, 刘艳霞, 王肇民. 质量阻尼器的发展[J]. 力学进展, 2003, 33(2):194—206.
Li Chunxiang, Liu Yanxia, Wang Zhaomin. A review on mass dampers[J]. Advances in Mechanics, 2003, 33(2):194—206.
[4] 谢绍松, 张敬昌, 钟俊宏. 台北101大楼的耐震及抗风设计[J]. 建筑施工, 2005, 27(10):7—9.
Xie Shaosong, Zhang Jingchang, Zhong Junhong. Aseismatic and wind-resisting design for Taipei 101[J]. Building Construction, 2005, 27(10):7—9.
[5] Chen Y, Cao T, Ma L, et al. Structural vibration passive control and economic analysis of a high-rise building in Beijing[J]. Earthquake Engineering & Engineering Vibration, 2009, 8(4):561—568.
[6] 顾金钧, 赵煌澄, 邵克华. 九江长江大桥应用新型TMD抑制吊杆涡激[J]. 土木工程学报, 1994, 27(3):3—13.
Gu Jinjun, Zhao Huangcheng, Shao Kehua. Application of new TMD to suppressing vortex-shedding vibration of hangers of Jiujiang bridge over Yangtze River[J]. China Civil Engineering Journal, 1994, 27(3):3—13.
[7] 徐 刚, 王靖夫, 任文敏,等. 施工中大桥桥塔的TMD减振研究[J]. 工程力学, 2003, 20(6):106—110.
Xu Gang, Wang Jingfu, Ren Wenmin, et al. Reduction of vibration during construction of bridge towers by TMD[J]. Engineering Mechanics, 2003, 20(6):106—110.
[8] 樊健生, 陈 宇, 聂建国. 人行桥的TMD减振优化设计研究[J]. 工程力学, 2012, 29(9):133—140.
Fan Jiansheng, Chen Yu, Nie Jianguo. Optimum design of tuned mass damper for footbridge[J]. Engineering Mechanics, 2012, 29(9):133—140.
[9] 张 晶, 王志强, 范 进, 等. 调谐质量阻尼器(TMD)在大跨斜拉桥减震控制中的应用[J]. 工业建筑, 2007, 37(Z1):292—294.
Zhang Jing, Wang Zhiqiang, Fan Jin. Application of tuned mass damper for controlling vibration of a stayed-cable bridge under earthquake excitation[J]. Industrial Construction, 2007, 37(Z1):292—294.
[10] Xing Chenxi, Wang Hao, Li Aiqun, et al. Study on wind-induced vibration control of a long-span cable-stayed bridge using TMD-type counterweight[J]. Journal of Bridge Engineering, 2014, 19(1):141—148.
[11] Wang Hao, Hu Ruomei, Xie Jing, et al. Comparative study on buffeting performance of Sutong Bridge based on design and measured spectrum[J]. Journal of Bridge Engineering, 2013, 18(7):587—600.
[12] Ernst H J. Der e-modul von seilen unter berücksichtigung des durchhanges[J]. Der Bauingenieur, 1965, 40(2):52—55.
[13] American ANSYS Corporation. ANSYS Advanced Analysis Techniques Guide, Release 9.0[M]. Canonsburg: ANSYS Inc., 2005.
[14] 范立础, 胡世德, 叶爱君. 大跨度桥梁抗震设计[M]. 北京:人民交通出版社, 2001.
[15] 公路桥梁抗震设计细则(JTG/T B02-01—2008)[S]. 北京:人民交通出版社, 2008.
Guidelines for seismic design of highway bridges (JTG/T B02-01—2008)[S]. Beijing:China Communications Press, 2008.
