一种医学生理微小流量电磁信号放大滤波电路与实现

郑乐一 赵永根 浙江大学医学院附属儿童医院 信息科 （浙江 杭州 310006）

在设计生产过程中，射流流量仪表在流量测量领域中，以其稳定可靠、响应速度快显示出了它的特点。该流量仪表输出的微小电磁信号是一个重要参数，但对其检测和控制又因其微小而显得比较困难。然而在仪表或控制系统中这些参数精度又都很重要，所以在实际测试中设计了此电路。

1.研究内容和方法

本文是针对一种电磁信号的检测需求，即在管道中的一个流量仪表具有一个稳定的磁场，介质流过磁场时形成电动势，若介质流速周期变化，其电动势会周期变化，但其强度非常微弱，为了检测该信号，设计了该放大电路，希望把这种微弱的、周期变化的电信号检测出来，通过测量电动势的周期频率来计算介质流速。

要获取不同流速下流量仪表较准确的输出信号，得通过放大滤波电路，然后采用傅立叶变换方法对输出信号进行处理，建立介质流量和输出频率的关系，求出基本误差，然后，对放大滤波电路进行性能评价。

2.信号采集原理

如图1所示，流体在振荡腔内产生稳定振荡，获得与体积流量成正比的流体振动频率。在侧壁两边有小磁块，流量计的腔体内就会产生一个磁场，期间介质不断地通过磁场，产生连续的感应电动势，电极两端将会产生以相同频率变化的电压，通过测量电极两端的电压频率，可以得到腔体内流体的振荡频率。

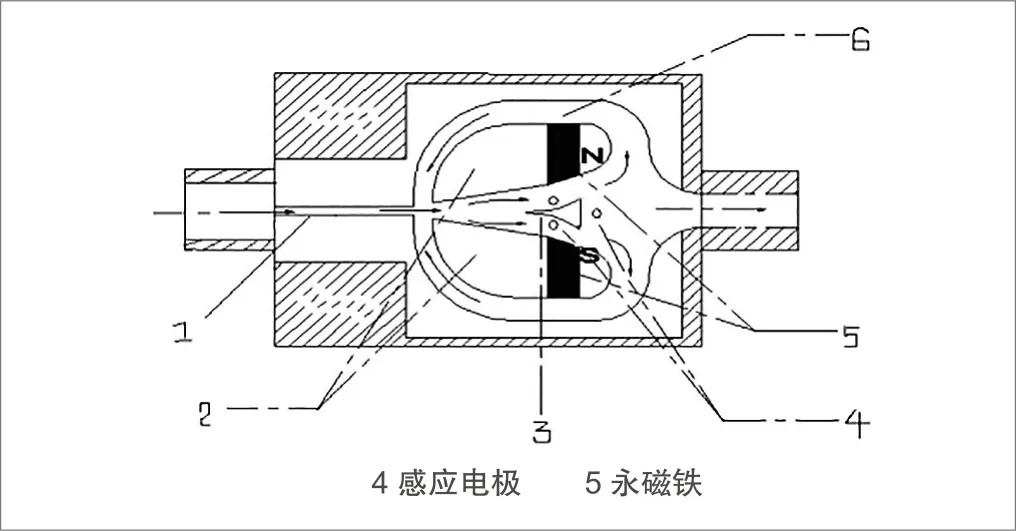
图1. 仪表原理图

3.快速傅立叶变换

快速傅立叶变换（FFT）计算速度较为高效，被广泛运用于数字信号的实时处理中。

设一种模拟信号x(t)，其连续的时间傅里叶变换（频谱）为：

设x(t)抽样后为x(nT)，T为采样周期，x(nT)的DTF可以表示为：

其中W=e-j2π/N，设{x(n)}为输入信号序列，采样点数总满足N=2m，用二进制表示（2）式中n和k，n=(nm-1,nm-2,…n0)，k=(km-1,km-2,…k0)；其中ni，ki为0或1，i=0,1,…nm-1。代入（2）式得：

通过该方法，总的运算次数为N/2Log2N，表明了FFT算法DFT更高效，更快速。

4.采样定理

采样定理即香农采样定理，基本的表述方式是时域采样定理和频域采样定理，它给出了从离散信号还原到连续信号所必须的最低采样频率，因此采样定理在离散系统设计中具有较重要的作用。

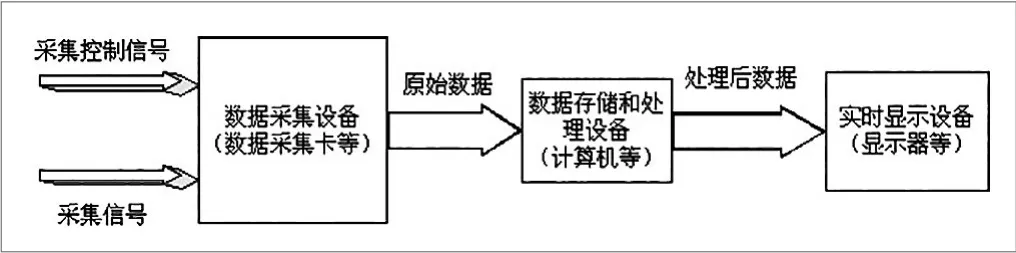
图2. 数据采集系统整体框图

如果采样频率ωs=2π/T0大于或等于2ωmax，则采样离散信号ε*(t)能无失真地恢复到原来的连续信号ε(t)。实际中，一般取2.56～4倍的信号最大频率。

5.数据采集

以嵌入式计算机和数据采集卡为基础，操作系统采用32位动态连接库驱动程序，采用VC6.0实现对数据采集卡控制，包括数据采集系统对话，系统运行方式、采集周期等参数的设置。

数据采集系统，通过基于PCI总线技术的数据采集卡采集传感器输出的模拟信号，并将模拟信号转换成数字信号。然后送入计算机进行处理，得出所需的数据。见图2。

通过MATLAB实现信号采样与计算，其中检测频率点（5、10、15、20、25、30、35、40、45、50、60、70）Hz。

6.放大滤波电路设计

从流量计电极两端引出的信号是微小流量信号，显示仪器较难观测到信号频率，须对该微量信号进行放大处理，为此，设计了该放大滤波电路，其各部分的功能：

首先，信号先经过一个放大电路，如图3所示。

正极信号和负极信号分别从J3、J4接入，J5接共地端，该放大电路中，采用了INA122仪表放大器。

其中INA122主要用于要求高精度、低噪声的差分信号放大。其中两个运放电路使其能够在保持性能良好的前提下，具有非常低的静态电流。

据图4，由于测试设计的电路为单电源，电路中不允许有负电压出现，所以在Ref引脚上接了的电压，这时

电路中，前置放大器的倍数一般不能超过25倍，所以RG的选择一般在15～50kΩ，使放大倍数控制在20倍以内。

信号经过一个放大电路后接入了两个串联巴氏滤波电路，形成四级低通滤波，具有更好的滤波效果。

其中巴氏滤波电路如图5所示，其极限频率为ω0 = 1/

图3. 放大电路图

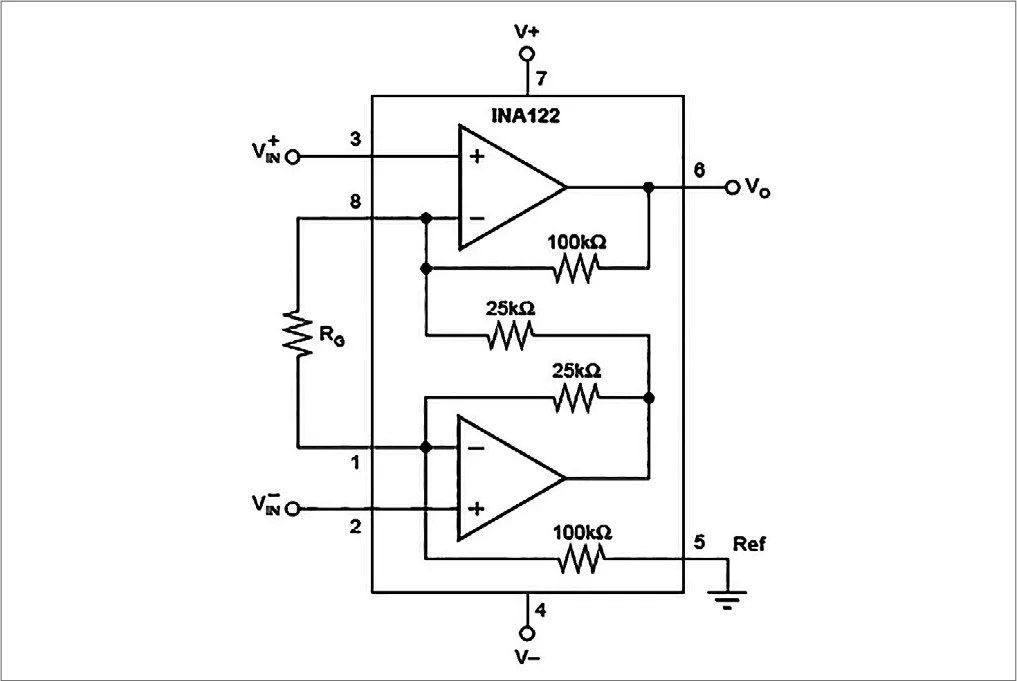
图4. INA122内部结构图

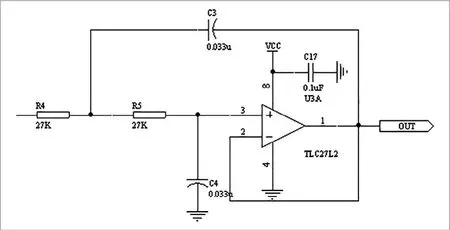
图5. 巴氏滤波电路

图6. 高通滤波放大电路

图7. 高速采集系统参数设置

接着再将信号接入一高通滤波及二级放大电路输出，如图6所示。其允许下限频率约为5Hz，二级放大倍数一般控制在30倍以内。

7.电路性能测试

用信号发生器对电路板提供信号源，由于检测信号为微小介质信号，故信号源提供的电压峰峰值不能很大，应为mV级。同时线路板还会存在着较大的干扰，所以在电源电压输入时选择了峰峰值为100mV的正弦信号源。

在信号源峰峰值不变的情况下，调节信号频率，其频率在1～100Hz范围内变化。

信号发生器的信号接入采集卡，由软件对采集起始通道和通道数进行选择，且设置输入电源电压范围，采样频率及采样点数，如图7所示。

运行程序采集信号，数据自动保存，再载入到MATLAB，通过FFT变换计算出信号的频率值。进行频谱显示，测得的（5、10、15、20、25、30、35、40、45、50、60、70）Hz信号频谱图，如图8～19。

表1列出了经过FFT变换后的信号频率值及误差分析。

图8. 5Hz频谱图（5.015Hz）

图9. 10Hz频谱图（10.01Hz）

图10. 15Hz频谱图（15.015Hz）

图11. 20Hz频谱图（20.02Hz）

图12. 25Hz频谱图（25.024Hz）

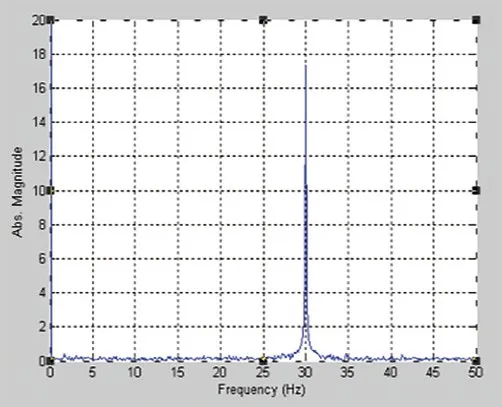
图13. 30Hz频谱图（30.029Hz）

图14. 35Hz频谱图（35.034Hz）

图15. 40Hz频谱图（40.039Hz）

图16. 45Hz频谱图（45.044Hz）

图17. 50Hz频谱图（50.049Hz）

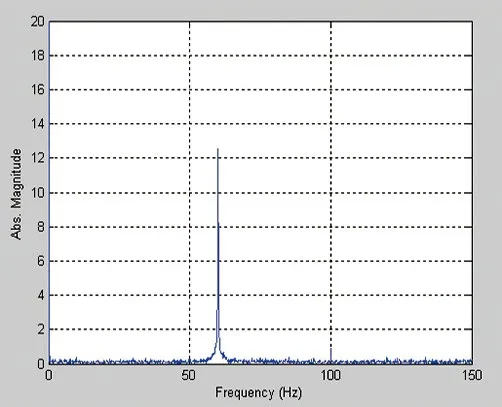
图18. 60Hz频谱图（60.059Hz）

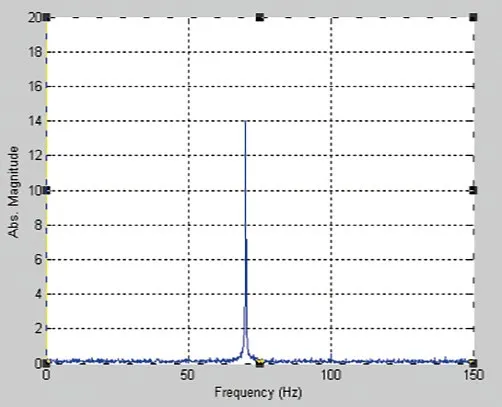
图19. 70Hz频谱图（69.946Hz）

8.结论

从信号频谱图和表1可以看出，微弱电磁信号经放大滤波电路处理后和FFT计算后的最大相对误差最大在0.3%以内，说明设计的放大滤波电路可以对100mV左右内的电磁信号进行放大滤波处理，且效果良好，达到了初始设计该电路的目的。

在医学领域，对生理量的检测有时需要用到对微小流量或者其流速的检测，该微小量流量仪表及其微小信号放大滤波电路会有着一定的应用前景。

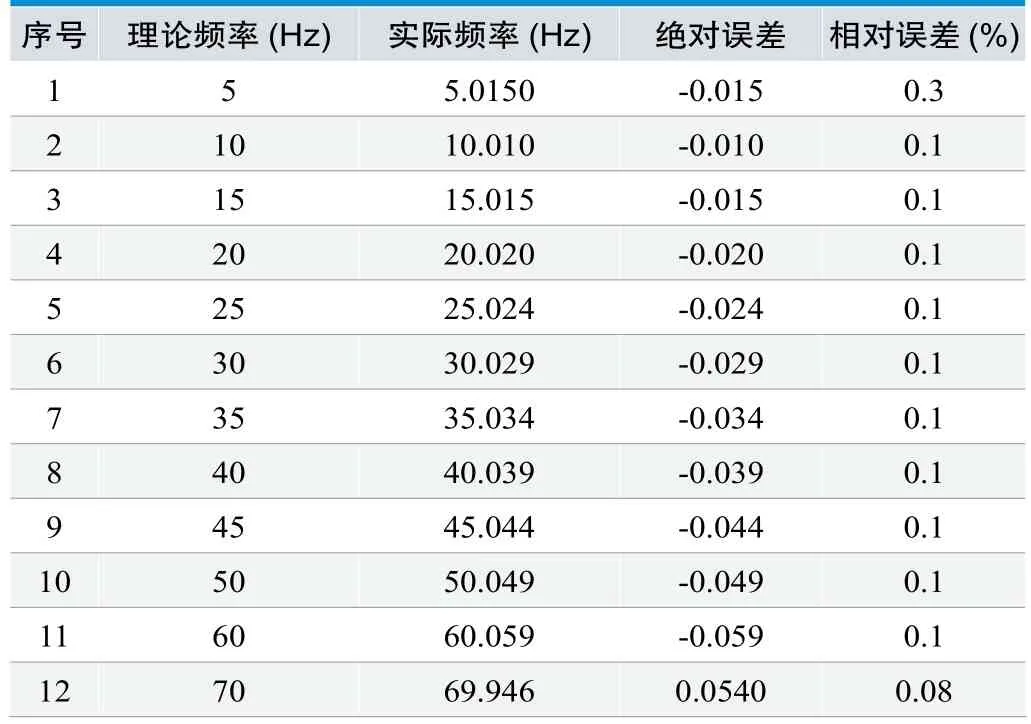
表1. FFT变换后的信号频率值及误差

[1] 周云波,林加端.射流流量计的原理及发展[J].中国仪器仪表,1997,18(11):3-5.

[2] 祁惠峰,赵静野.新型结构的射流流量计的实验研究[J].计量技术,2004,1(8):3-4.

[3] 石焕,戴华平,李志明,等.电磁式射流流量计[P].中国专利:101067564A,2007-11-07.

[4] 梁国伟,蔡武昌.流量测量技术及仪表[M].北京:机械工业出版社,2002:62-270.

[5] 甘秋歌.快速傅立叶变换(FFT)的另一种推导方法及实现[J].西南民族大学学报,2007,32(2):275.

[6] 刘文生,李锦林.取样技术原理与应用[M].北京:科学出版社,1981:15-17.

[7] 费业泰.误差理论与数据处理[M].北京:机械工业出版社,2004:123.

[8] Park.GJ,许庆.射流流量传感器在工业上的应用[J].国外计量,1991,19(5):33-35.

[9] 傅新,王驰宇,谢海波,等.射流流量计的仿真与试验研究[J].机械工程学报,2006,42(7):24-29.