基于数值模拟的隧道施工方案比选

2018-07-05刘希亮孙飞跃

土木工程与管理学报 2018年3期

刘希亮，孙飞跃

(河南理工大学土木工程学院，河南焦作 454003)

随着城市人口数量的快速增长，城市交通拥堵现象严重，地铁交通成为改善地面交通拥堵现象的必然选择。地铁隧道一般埋深较浅，不能有效形成压力拱，如果未采取合理的施工方案就会造成较大的地表沉降，导致地表建筑物倾斜或者地面道路下陷。因此，选择最佳的施工方案对保证隧道施工的顺利进行具有重要意义。

近年来，学者们不断地对隧道施工方案的合理性进行探索，并取得了长足的进步。李振东等[1]选取了CRD工法和短台阶工法两种施工方案对地铁隧道进行了施工模拟，发现采取合理的支护形式可以有效地控制隧道拱顶的竖向位移。石熊等[2]在CRD工法的前提下，通过比较不同施工顺序所得到的围岩水平位移和拱底竖向位移及其应力的变化得到了适合该隧道的施工方案。任建喜等[3]采用FLAC3D数值模拟和现场检测相结合对CRD法开挖所产生的地表位移变化进行探究，得到了较为合理的位移控制措施。

本文采用FLAC3D有限差分软件建立隧道计算模型，同时采用三种不同的施工方案进行模拟施工。通过对比分析，优选出合适的施工方案。

1 工程概况

某城市地铁隧道下穿城市主干道，隧道断面的宽度12.6 m，高度10.3 m，隧道最大埋深24 m。为了降低施工过程中对隧道围岩的扰动和减小对地面造成沉降。同时，为了保证施工的顺利进行，在开挖前采用大管棚与小导管注浆相结合的超前支护形式。施工过程中采用分步开挖，逐步支护的方法。当最后一部开挖完成后拆除临时隔壁，衬砌封闭成环。施工过程中严格遵循“管超前、严注浆、短开挖、强支护、快封闭、勤量测”的基本原则[4]。具体隧道围岩和支护结构物理力学参数根据有关文献[5～8]取值，见表1所示。

表1 隧道围岩和支护结构物理力学参数

2 数值模拟

2.1 FLAC程序简介

FLAC3D是采取输入命令的方式驱动程序运算，命令字控制着程序的运行。有别于一些软件采用输入数据的方式控制程序运行。运用FLAC3D建立计算模型时，需要进行：生成有限差分网格、选择本构特性和设置材料参数、给定模型的边界条件和初始条件这三方面的任务。完成以上任务后，能够获得模拟工程开挖前的初始应力状态。而后进行的工程反映分析需要工程开挖或改变模拟边界条件来完成。最后，对计算结果进行分析与总结[9,10]。

FLAC3D是以显式拉格朗日连续介质法和混合-离散分区技术为基本理论，因此能够很精确地模拟材料的塑性破坏和流动。因为FLAC3D在计算过程中不需要形成刚度矩阵，所以解决大范围的三维问题只需较小的计算空间。该软件可用于求解大变形的非线性岩土力学问题，能够解决一般有限元分析程序难以解决的岩土材料大变形和破坏的问题。但是，在求解线性问题时，比有限元法运行所需要的时间长。本文正是运用FLAC3D有限差分软件对该隧道工程变形的非线性岩土问题进行模拟。最后，通过对比分析不同的施工方案得出适合该工程的开挖方案。

2.2 建立模型

由于隧道是纵向尺寸较长，横向断面尺寸较短的地下结构物，故而在研究过程中不考虑开挖进尺对施工的影响。因此，在计算分析中，沿隧道纵深方向选取10 m长的隧道作为研究对象。

根据圣维南原理，建立的计算模型横向长100 m，竖向高60 m，纵向长10 m，即左右边界为4倍左右隧道总跨度，下部边界为3倍左右隧道总高度，隧道上边界为地面[9]。整个模型共17034个六面体单元，18126个网格节点。在数值计算中，采用Mohr-Coulomb材料模型，初期支护采用cable单元和shell单元共同模拟，开挖模拟采用空模型。该计算模型的上边界为自由边界，其余边界均为位移约束边界条件。隧道模型及边界条件如图1所示。

2.3 开挖方案模拟

本文为了研究不同开挖方案对隧道周围岩体的影响，分别采用三种不同的施工方案进行数值模拟。最后，通过分析计算结果，得出了较为合理的施工方案。

采用CRD法、CD法、台阶法三种施工工法。开挖过程中采用分步开挖，逐步支护的方法，具体开挖方案如图2所示。

3 计算结果分析

3.1 围岩位移分析

隧道围岩位移变形是隧道开挖过程中的重点控制对象。如果位移变形较大会影响隧道的正常使用，从而增加了对人力、财力和物力的浪费。

图1 计算模型/mm

图2 三种施工方案开挖顺序

在三种不同施工方案下，隧道的竖向位移和水平位移云图如图3，4所示。通过分析图3可知，三种不同的施工方案在拱顶和拱底处发生的竖向变形最大，所以在开挖中应该特别注意此处的围岩变形。还可以看出，采取台阶法开挖时拱顶最大竖向位移变化量最大，CRD法次之，CD法最小。而在拱底中心处CRD法施工和台阶法施工所引起的底鼓现象最为严重，CD法施工比CRD法和CD法施工所引起的底鼓现象较轻。主要原因是台阶法施工时把隧道上半部分土体开挖掉没有保留预留核心土，从而核心土对拱顶位置没有约束导致了拱顶变形变大。而CRD法施工时，开挖的各个分部封闭成环的时间较短，中间隔壁墙能有效抑制围岩的变形，在拱顶、拱底处的变形起到了关键作用[11]。但是由于CRD法施工的多次开挖增加了对土体的扰动次数，因而拱顶的竖向位移变化量比CD法施工大。通过分析图4可知，隧道两侧横向变形主要是向隧道外侧发生位移，这与文献[12～14]计算得到的结果是一致的。而且，隧道左右两侧横向变形大致呈对称分布。隧道拱顶位置受力类似于压力拱，将其受到的压力转化为水平推力，导致围岩向外侧移动。最终造成隧道拱顶承受主动土压力，而侧墙向外移动挤压使岩体承受被动土压力。

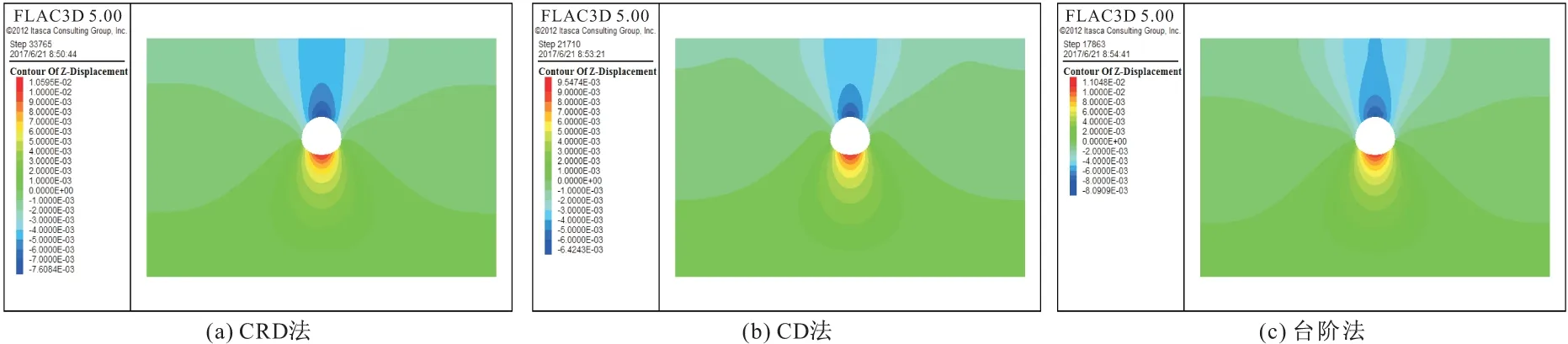
图3 三种施工方案下隧道竖向位移云图

图4 三种施工方案下隧道水平位移云图

将三种施工方案所引起的隧道拱底、拱顶和左右两侧变形进行监测(监测点为1，2，3，4，如图5所示)，分别列于表2，3中。从表2可以看出：在支护形式相同的条件下，CD法施工比台阶法和CRD法施工引起的拱顶和拱底沉降变形略小。也可以看出，CD法施工引起的拱顶沉降比CRD法施工小1.19 mm，比台阶法施工小1.67 mm。CD法施工引起的拱底沉降比CRD法施工小1.05 mm，比台阶法施工小1.45 mm。从表3可知，三种施工方案下台阶法施工对隧道两侧横向变形影响较小，相比其他两种方案略有优势。虽然CD法在两帮处产生的变形相比其他方案最大，但位移量数值还是比较小的。在开挖过程中，一定要加强对拱顶的支护，做到边开挖边支护以减小拱顶的沉降量。总体来说，CD法施工与其他两种方案相比更具有控制围岩变形的优势。

表2 三种工法下拱顶、拱底沉降变形 mm

表3 三种工法下隧道两侧横向变形 mm

在数值模拟计算中对隧道拱肩水平和竖向位移进行及时监测(监测点为5，6，7，8，9，10，如图5所示)。绘制出拱肩水平和竖向位移曲线，如图6，7所示。通过分析图6可知，CRD法施工时在隧道拱肩位置所产生的水平位移量最大，最大处为3.09 mm；CD法施工时所产生的位移量最小，最大水平位移量为2.47 mm。通过分析图7可知，台阶法施工时在隧道拱肩位置所产生的竖向位移量最大，最大处为6.51 mm；CD法施工时所产生的位移量最小，最大竖向位移量为4.68 mm。因此，从水平和竖向位移量来看，CD法施工优于其余两种方案。

图5 位移监测点

图7 拱肩竖向位移曲线

为了优选出一个更加适合于该隧道的施工方案，控制地表沉降，不影响地面建筑物和道路的正常使用。因此，隧道施工过程中必须严格控制地表沉降。在数值计算过程中，在距隧道中心轴线左右各50 m的地表每隔5 m设置监测点，绘出地表不同位置沉降曲线(图8)。由图8可以看出，三种施工方案在隧道中线左右两侧40 m范围内造成的地表沉降量比较大，在隧道中心轴线位置处地表沉降量最大。隧道中心轴线左右两侧40 m之外的地表沉降量随距离中心轴线越远变化越不明显，可以看出隧道开挖对地表沉降影响的区域大致为隧道跨度的3倍左右。

比较三种方案在地表不同位置引起的沉降，CD法施工在地表不同位置产生的沉降量最小的，台阶法施工在地表不同位置产生的沉降量是最大，在中线位置处最为明显，CD法施工比在台阶法施工下产生的沉降量降低12.7%。这也说明，该隧道采用CD法施工时不仅可以控制围岩的位移变形还可以简化开挖步骤从而提高工作效率。

图8 地表不同位置沉降曲线

3.2 围岩应力分析

洞室开挖后，围岩产生应力重分布，破坏原有的平衡状态，使围岩局部应力增加[15]。因此，隧道围岩应力状态也是隧道施工中要考虑的重要内容。三种施工方案的竖向和水平应力云图如图9，10所示。根据应力云图可知，最大压应力发生在隧道的最底部，隧道的顶部出现了拉应力。在隧道两帮与地面的交接处发生了应力集中现象，此时应特别注意应力集中部位岩体的加固，防止应力集中而产生局部破坏[16]。从中也可以看出隧道拱顶处的受力状态明显好于隧道拱底处的受力状态。由图9可知，CD法施工造成的应力集中现象较轻，台阶法施工造成的应力集中现象较重。CD法在隧道开挖完成后造成的围岩最大压应力为1.22 MPa，CRD法在隧道开挖完成后造成的围岩最大压应力为1.46 MPa，台阶法在隧道开挖完成后造成的围岩最大压应力为1.83 MPa。相比之下，CD法施工比台阶法施工产生的最大压应力降低了33.3%。由图10可知，在隧道的拱顶、拱底和两帮处都有应力集中现象。相比之下，CD法开挖的应力集中现象较轻，而台阶法开挖的应力集中现象较为严重。

图9 三种施工方案下隧道竖向应力云图

图10 三种施工方案下隧道水平应力云图

为了确保施工的顺利进行，也应对开挖后隧道的主应力进行分析，主应力云图如图11，12所示。由主应力云图可知，最大主应力主要分布在隧道顶部、底部和地面与侧墙交接处，最小主应力主要分布在隧道底部和两帮处。因此，在施工过程中应该特别注意这些部位的围岩加固，防止围岩发生破坏造成不必要的损失。

图11 三种施工方案下最大主应力云图

图12 三种施工方案下最小主应力云图

3.3 围岩应变分析

由于岩体中有结构面的存在，从而对岩体的剪切强度特性有所影响。因此，应对围岩的剪切应变和主应变增量进行分析，应变云图如图13，14所示。由应变云图可以看出，CRD法开挖时，在隧道拱顶和拱底处主应变增量较大，在隧道两帮和隧道底部处剪切应变增量较大；CD法施工时，在隧道拱顶、拱底和侧墙处主应变增量较大，在隧道地表和隧道两帮与拱底交接处剪切应变增量较大；台阶法施工时，在隧道拱底、拱顶和两隧道帮处的主应变增量较大，在隧道拱顶和隧道两帮与拱底交接处剪切应变增量较大。相比之下，CD法施工主应变和剪切应变增量相对较小，更适合于该隧道的施工。在隧道拱底位置和两帮处的剪切应变形成了曲线形状的剪切带，此位置附近容易发生剪切破坏。隧道拱顶处的剪切变形明显比隧道拱底处的剪切变形有利，随着整个隧道开挖完成剪切带逐渐趋于稳定[17]。

图13 三种施工方案下主应变云图

图14 三种施工方案下剪切应变云图

4 结论

采用FLAC3D有限差分软件对三种施工方案进行了数值模拟，并根据隧道开挖过程中围岩位移变化、围岩应力变化、围岩应变变化、拱顶位移和地表沉降变化等五个方面综合考虑，得到了如下主要结论：

(1)通过围岩位移变化可得，CD法施工时竖向和水平位移变化量比其他两种施工方案较小，从拱肩位移监测来看，CRD法施工时产生的位移变化量最大而CD法最小。从拱底沉降分析来看，CD法施工具有沉降量小的优势。地表最大沉降量为9.55 mm，台阶法产生的最大沉降量为11.0 mm，CRD法下的最大沉降量为10.46 mm。相比之下，CD法比台阶法沉降量降低13.2%，比CRD法沉降量降低10.0%。因此，从围岩位移变化来看，CD法施工方案优于其余两种施工方案。

(2)通过围岩应力变化可得，在隧道两帮与隧道地面的交接处和开挖拱顶、拱底部位易产生应力集中现象，这与大量工程实际相吻合。根据模拟结果，应对应力集中部位进行重点支护，以免造成围岩和支护结构的局部破坏。而CD法施工时所产生的应力集中现象较轻。CD法在隧道开挖完成后造成的围岩最大压应力为1.22 MPa，CRD法在隧道开挖完成后造成的围岩最大压应力为1.46 MPa，台阶法在隧道开挖完成后造成的围岩最大压应力为1.83 MPa。相比之下，CD法比台阶法的最大压应力降低了33.3%。因此，从围岩应力变化来看，CD法施工方案优于其余两种施工方案。采用CD法施工时，不仅可以加快施工进度，还可以避免各分部施工对隧道的干扰。

(3)通过围岩应变分析可得，在隧道开挖时边墙处会形成一个双曲线形状的剪切带。这是由于岩体中节理的存在，使岩体沿节理面产生破坏。但是，随着整个隧道开挖完成剪切带逐渐趋于稳定。

(4)从地表不同位置沉降曲线图来看，CD法施工方案在地表的每一个位置产生的沉降量都较其余两种施工方案产生的沉降量小。在距离隧道中线40 m范围内地表产生的沉降量较大，可以看出隧道开挖对地表沉降影响的区域大致为隧道中线两侧3倍跨度左右。

[1] 李振东, 李辉, 王健. 地铁隧道支护系统的数值模拟研究[J]. 地下空间, 2004, 24(1): 19-22.

[2] 石熊, 张家生, 刘宝琛. 大断面浅埋偏压隧道CRD法施工工序研究[J]. 现代隧道技术, 2015, 52(3): 193-199.

[3] 任建喜, 万永涛, 张扬洋, 等. 大断面黄土地铁隧道CRD法施工诱发的地表沉降规律[J]. 城市轨道交通研究, 2015, 18(10): 21-26.

[4] 任建喜. 地下工程施工技术[M]. 西安: 西北工业大学出版社, 2012.

[5] 丁锐, 范鹏, 焦苍, 等. 不同开挖步骤引起浅埋隧道地表沉降的数值分析[J]. 铁道工程学报, 2005, (5): 62-65.

[6] 张莉. 隧道施工由CRD改为CD工法衬砌结构内力及变位分析[J]. 地质与勘探, 2007, (2): 93-98.

[7] 周隽. 矩形隧道施工引起的地表变形分析[J]. 地下工程与隧道, 2006, (2): 20-22.

[8] 张国亮, 韩雪峰, 陈登伟, 等. 暗挖地铁车站大断面隧道施工过程的数值模拟研究[J]. 四川建筑科学研究, 2015, 41(3): 54-57.

[9] 李围. 隧道及地下工程FLAC解析方法[M]. 北京: 中国水利水电出版社, 2009.

[10] 陈育民, 徐鼎平. FLAC/FLAC3D基础与工程实例[M]. 北京: 中国水利水电出版社, 2013.