基于多目标混沌云布谷鸟算法的HAPF优化研究
2018-07-05马艺元宋卫平宁爱平邓华龙
马艺元,宋卫平,宁爱平,邓华龙
(太原科技大学 电子信息工程学院,太原 030024)
众多电力电子设备的使用以及电力系统中存在的非线性负载给电网带来造成严重的谐波危害。因此,研究谐波的治理问题对供电设备和用户设备的正常使用来讲意义重大,有很好的应用前景。谐波的治理大体分为两类:主动抑制和被动治理。主动抑制以造成谐波的各种设备为出发点,优化电力电子设备,尽量达到产生较少或不产生谐波的目标;被动滤除则要在电力系统中安装一些滤波装置[1]来滤除谐波。但是前者难以实现,成本高,操作难度大,所以现有方法中仍以引入电力滤波器为主。混合有源滤波器(Hybrid Active Power Filter,HAPF)[2]结合了无源支路能滤除系统主要的低次谐波和有源滤波器能滤除系统中剩余的少部分高次谐波的特点,最终可达到较好的谐波治理的效果,是目前主要使用的滤波设备。
混合有源电力滤波器的综合设计既需要考虑其经济指标,又要看最后补偿效果,是典型的多目标、非线性优化问题。因其具有广泛的应用前景,对它的优化是非常有必要的。2010年,文献[3]将粒子群算法应用到HAPF的无源滤波器中,滤波效果得到明显提高,但未充分考虑有源滤波器部分;2010年,文献[4]和[5]分别基于量子粒子群算法及遗传算法-粒子群算法对并联混合有源滤波器进行了优化,但没有优化混合有源滤波器的结构;2011年,文献[6]等用菌群-粒子群算法来优化HAPF中的无源滤波器部分,达到了一定的理想效果,但算法易陷入局部最优。鉴于多目标布谷鸟搜索算法能够避免上述常规算法的缺点,再结合混沌云模型的全局优化功能,采用改进的混沌云模型多目标布谷鸟算法对谐振注入式并联混合有源滤波器进行了优化,将HAPF的经济成本及维护费用、无功功率补偿容量及滤波效果看作多目标满意度函数,通过Matlab/Simulink仿真软件和其他算法做了比较,综合验证设计的实用性和可行性。
1 混合有源滤波器多目标优化模型
1.1 谐振注入式并联混合有源滤波器
根据电网谐波情况,主要存在低次谐波及少量高次谐波,综合设计了由五次、七次单调谐无源滤波器与二阶减幅高通滤波器组成无源部分,然后注入支路与APF经过耦合变压器串联后挂在10 kV母线上的谐振注入式并联混合有源滤波器,如图1所示。
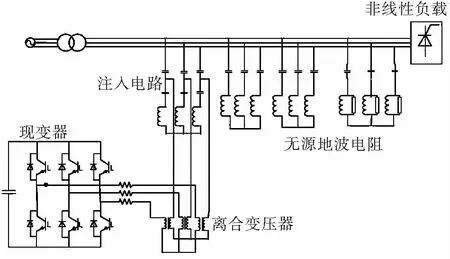
图1 谐振注入式并联混合有源滤波器
Fig.1 Injected type hybrid active power filter
1.2 HAPF多目标优化模型
1)经济性函数:将滤波每部分的造价及维护费用综合考虑,作为经济型的指标。HAPF造价大部分是电感和电抗的费用,一是初期的装设费用,二是后期的维护费用。目标函数为下式:
minF
F=KC(QC1+QCC+QCL+QCN)+KL(QL1+QLL)+KQWQC+KLWQL
(1)
式中,QLL、KL分别为电容和电感的单位造价,C1、CC、CL、CN各自对应注入部分、谐振支路、无源滤波部分以及逆变器直流侧的电容,KQWKLW是电容电感的维护费用,QL1、QLL分别为注入支路和无源支路的电感参数。
2)满意度函数:满意程度主要由性能来决定的,引入HAPF后,目标是达到电网谐波含量低于国家标准,使统电压和电流总谐波畸变率符合国标(GB/T14549-1993),且越低越好。
(2)
式中,THDU、THDi分别对应电压电流的谐波畸变量,THDu,max、THDi,max是国标电压电流总畸变的最大值。
3)无功补偿容量:用过无源滤波器和注入支路对系统进行补偿,要考虑补偿效果,补偿量要适度的同时要尽量使系统的功率因数Q接近1,即:
(3)
式中,∑Q包括PF和注入电容提供的无功。
1.3 约束条件
滤波器的优化应在一定的约束条件下进行,才能使得设计出来的HAPF满足要求,考虑HAPF的结构,具体的约束条件如下:
1)逆变器直流侧的电容

(4)
式中,Up为逆变器期望输出电压峰值。
2)逆变器 IGBT 开关频率
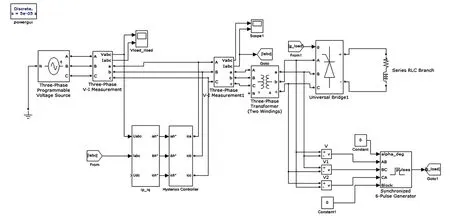
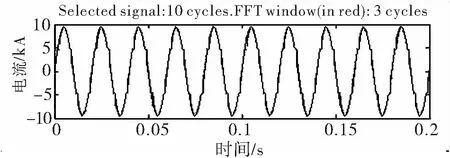
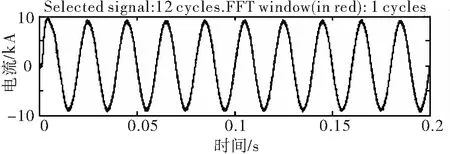
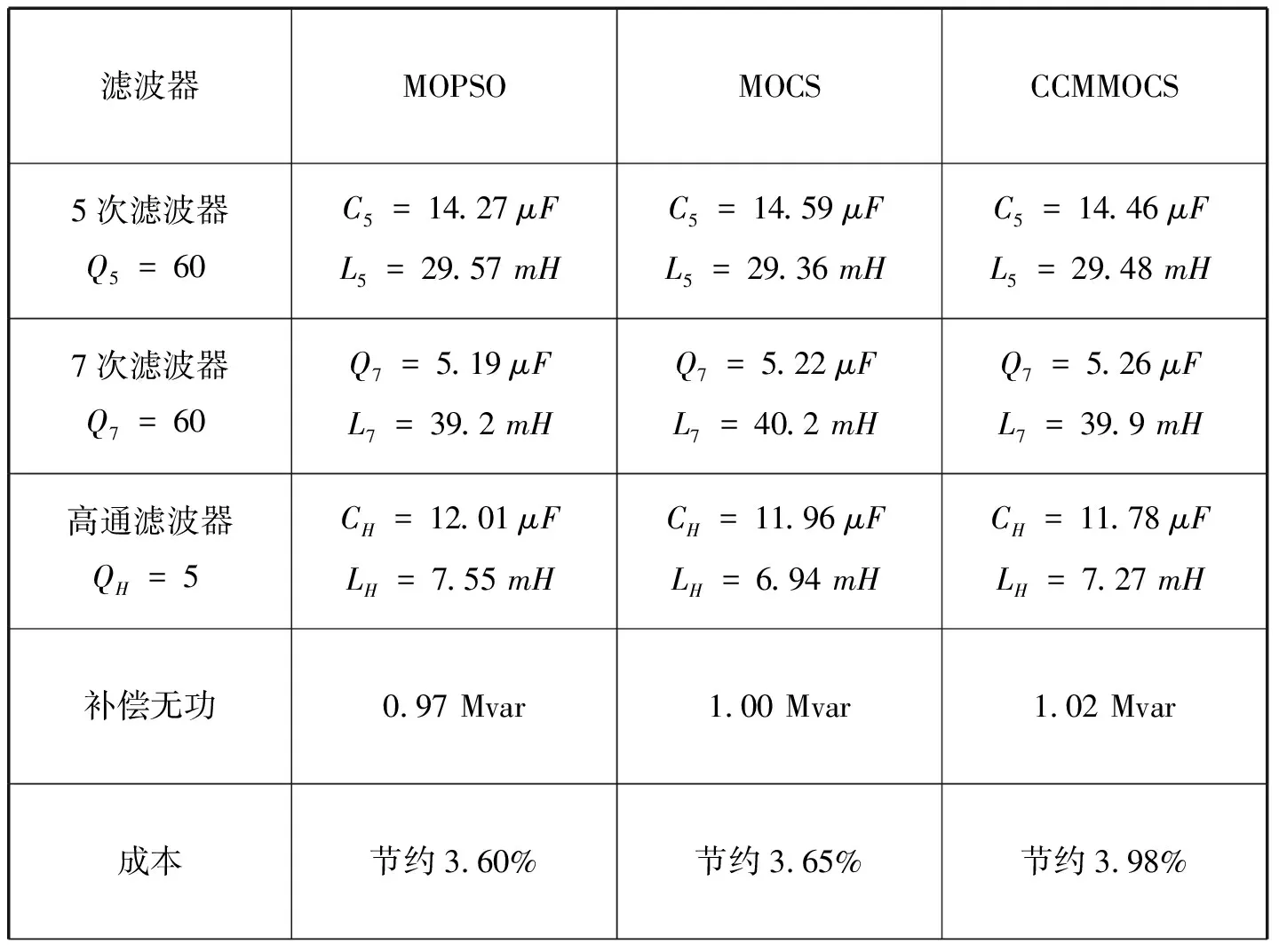
IGBT的开关频率与补偿电流的输出性能直接相关。过高会产生高频谐波,过低又无法满足输出要求。因而有Kmin (5) 式中,Kmin、Kmax是开关频率最小值、最大值。 2009年,由杨新社教授和Suach Deb教授提出了一种新的元启发式算法,名为布谷鸟搜索算法(Cuckoo Search, CS)[7].CS算法参数少、便于实现,现已经成功应用于工程设计、背包问题等领域并得到广泛关注。鉴于它的简单实用,2011年杨新社教授等人在CS算法基础上提出了多目标布谷鸟搜索算法(Cuckoo Search algorithm for Multi-objective optimization, MOCS)[8],思想主要表现在两点:对布谷鸟寄生育雏行为和鸟类或果蝇飞行模式的模拟。 在MOCS中,采用随机初始化产生初始鸟巢位置,具有较大的盲目性,解的质量不高,而仅采用莱维飞行[9]搜索机制更新鸟巢位置,在迭代后期收敛速度及精度无法满足优化需求。为解决上述问题,结合混沌云模型[10]来改进MOCS,提出混沌云模型多目标布谷鸟搜索算法(cuckoo search algorithm for multi-objective optimization based on chaos cloud model,CCMMOCS).首先在进化过程中通过混沌理论对一般的布谷鸟巢位置在全局中优化,以防落入局部最优;然后利用云模型[11-12]对较好的布谷鸟巢位置优化来提高精度;最后将两种方法对比得到相对更好的解作为最优值以完成优化。位置的好坏是利用布谷鸟现有位置和平均位置的目标函数值favg比较来得出的,如果现有布谷鸟巢适应度值小于平均目标函数值,即为位置较好;反之,如果现有布谷鸟巢适应度值大于平均目标函数值,则位置较差。综合考虑正态云发生器的随机性与倾向性平稳的优点,在优化时满足传统的优势同时加快寻优速度,并保持了前沿的均匀性和多样性。其中,期望Ex为位置较好的布谷鸟巢个体xi,为缩小搜索范围并提高算法稳定性,选取熵En=2xi,超熵He=En/5. 采用加权求和的形式将HAPF三个目标转化为单目标问题,进行归一化处理。其中,将单目标函数值作为要改进的鸟巢位置。为保证权重的取值合理性,权重由遍历而来。得到最优鸟巢位置后,再进行解归一,得出每个目标的最优值。 具体算法的步骤为: Step 1.(初始化)初始化维数m,鸟窝数量n,被其他鸟类发现并抛弃的概率Pa,迭代次数N_iter等; Step 2. (布谷鸟巢位置初始化) 随机初始化布谷鸟巢位置; Step 3.(运行MOCS算法) 种群中每个布谷鸟巢位置执行MOCS算法,如果满足结束条件,跳出循环; Step 4.(布谷鸟位置优劣比较) 不满足结束条件,启动混沌云模型,比较当前个体布谷鸟巢适应度和平均适应度值favg,分出位置较差布谷鸟巢和位置较好的布谷鸟巢; Step 5. (混沌理论优化) 位置较差的布谷鸟巢利用混沌理论优化。式(2)对位置较差的布谷鸟巢进行Logistic 映射产生新个体,产生更优解取代原位置; Step 6. (云模型优化) 位置较好的布谷鸟巢使用云模型来优化。把位置较好的布谷鸟巢个体作为n维正态云云发生器的输入,产生新的布谷鸟个体位置。如果为更优位置,更新最优值; Step 7.(替换最优值) 比较云模型和混沌理论分别寻优的值,选出最优值; Step 8. (终止条件) 如果满足结束条件,转向Step 9; 若不满足,N_iter=N_iter+1,返回Step 4; Step 9. (结束算法) 输出最优结果。 为了观察混沌云模型多目标布谷鸟搜索算法在HAPF多目标参数设计优化问题上的性能,选择测试环境为: Windows7,MATLAB2012a/SimulinK.表1为某变电站10 kV侧的A相谐波电流含量,从中看出5次、7次谐波含量较高,因此采用5次、7次的单调谐无源滤波器及二阶减幅高通滤波器作为无源滤波器部分。图2为整体仿真图。 表1 10 kV母线A相谐波电流检测值 Tab.1 Harmonic current of phase A in 10 kV bus 谐波次数实测值/A国家标准值/A562.1626.41728.0819.81915.5512.28118.1110.43136.037.92154.657.13178.25.94198.035.41 为验证算法的有效性,仿真时与多目标粒子群算法(Particle swarm optimal algorithm based on multi-objective optimization,MOPSO)[13]进行了对比。图1为未装设滤波器的电流图,图2、3分别为装设HAPF并用MOPSO算法改进参数后的混合有源滤波器电流图。由三幅幅图对比看出,谐波改善效果良好。图4、5和6分别为未装设HAPF,MOPSO算法和CCMMOCS算法优化参数后装设滤波器的频谱分析图。由几幅图对比得知,未装设HAPF的谐波畸变率为24.72%,远远高于国标要求,MOPSO算法及CCMMOCS算法改进参数后的谐波畸变率分别为2.42%和1.94%,CCMMOCS算法比MOPSO算法优化后还下降了0.48个百分点,谐波得到很好地抑制。表2中列出了MOPSO算法和CCMMOCS算法优化后的数据,可以看出经济成本得到很好控制,滤波效果及补偿效果也得到了提升,证明算法的改进有明显的效果及实用性。在算法复杂度分析方面,固定迭代为1000次后,CCMMOCS算法收敛速度要明显优于MOPSO算法及基本MOCS算法,说明CCMMOCS算法在HAPF的多目标优化中具有明显优势并且具有实用价值。 图2 系统仿真图 Fig.2 System simulation 图3 未装设HAPF前的电流图 Fig.3 Current without HAPF 图4 MOPSO算法优化后的电流图 Fig.4 Current after optimization based on MOPSO 图5 CCMMOCS算法优化后HAPF的电流图 Fig.5 Current after optimization based on CCMMOCS 图6 未装设HAPF的频谱分析图 Fig.6 Frequency spectrum analyses without HAPF 图7 MOPSO算法优化后的频谱分析图 Fig.7 Frequency spectrum analyses based on optimized MOPSO 图8 CCMMOCS算法优化后的频谱分析图 Fig.8 Frequency spectrum analyses based on optimized CCMMOCS 图9 不同算法下的收敛曲线 Fig.9 Convergence curve based on different algorithms 表2 混合滤波器设计参数 Tab.2 Design parameters of HAPF 滤波器MOPSOMOCSCCMMOCS5次滤波器Q5=60C5=14.27 μFL5=29.57 mHC5=14.59 μFL5=29.36 mHC5=14.46 μFL5=29.48 mH7次滤波器Q7=60Q7=5.19 μFL7=39.2 mHQ7=5.22 μFL7=40.2 mHQ7=5.26 μFL7=39.9 mH高通滤波器QH=5CH=12.01 μFLH=7.55 mHCH=11.96 μFLH=6.94 mHCH=11.78 μFLH=7.27 mH补偿无功0.97 Mvar1.00 Mvar1.02 Mvar成本节约3.60%节约3.65%节约3.98% 通过上述仿真结果对比得出,利用混沌云模型多目标布谷鸟搜索算法在注入式谐振混合有源滤波器的参数优化方面,比粒子群算法有明显优势,滤波效果得到明显提升,同时达到良好的无功补偿效果及好的经济效益,具有一定的实用价值和应用前景。 参考文献: [1] 徐亚朝,何秋生,王少江,等.一种改进的自适应卡尔曼滤波算法[J].太原科技大学学报,2016,37(3):163-167. [2] 黎燕,罗安.双谐振混合型有源电力滤波器特性研究[J].电工技术学报,2012,36(9):258-260. [3] 何娜,胡安,高强,等.大容量混合有源滤波器多目标优化设计 [J].电机与控制学报,2010,14(11):49-58. [4] 张国荣,李丹.基于量子粒子群优化算法HAPF参数的多目标优化[J].合肥工业大学学报,2010,33(8):1152-1157. [5] 江友华,廖代发,唐忠.混合有源滤波器多目标优化设计 [J]. 控制理论与应用,2010,27(7):916-923. [6] 李圣清,李永安,罗晓东,等.基于菌群-粒子群算法的混合有源滤波器中无源滤波器多目标优化设计[J].大功率变流技术,2011,4(1):13-18. [7] YANG X S, DEB S. Cuckoo search via Levy flights [C]//Proceeding of World Congress on Nature & Biologically Inspired Computing. India:Nabic, 2009:210-214. [8] YANG X-S, DEB S.Multi-objective cuckoo search for design optimization[J]. Computers & Operations Research,2011, 40(6):1616-1624. [9] 牛海帆,宋卫平,宁爱平. 莱维飞行与粒子群算法的结合[J].太原科技大学学报,2016,37(1):6-11. [10] DONG S F, DONG Z C, MA J-J. Improved PSO algorithm based chaos theory and its application to design flood hydrograph [J]. Water Science and Engineering. 2010, 3(2):156-165. [11] 李德毅,刘常昱. 论正态云模型的普适性[J]. 中国工程科学,2004,6(8):28-33. [12] 李志平,王勇,张呈志,等.云模型的布谷鸟搜索算法[J].计算机应用研究,2016,33(1):92-98. [13] 王强,赵志诚,桑博.基于改进粒子群算法的分数阶系统辨识方法[J].2014,35(3):198-201.2 基于混沌云模型多目标布谷鸟搜索算法的混合有源滤波器设计
2.1 多目标布谷鸟搜索算法
2.2 混沌云模型多目标布谷鸟搜索算法
2.3 优化变量选择
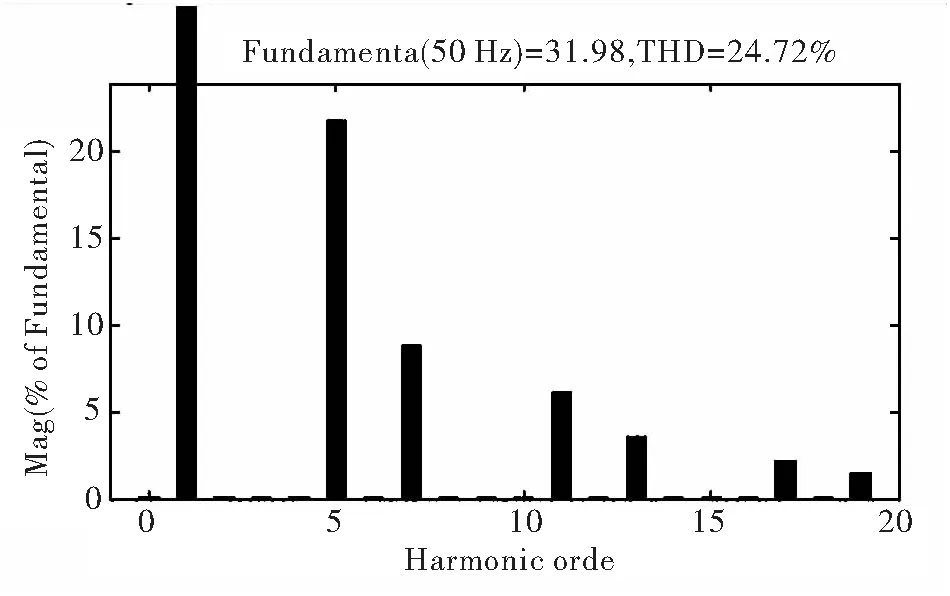
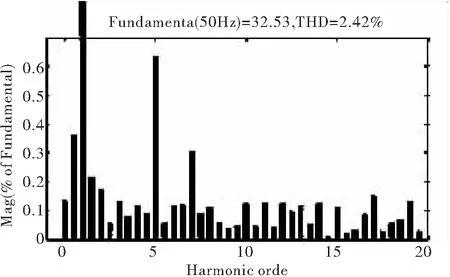
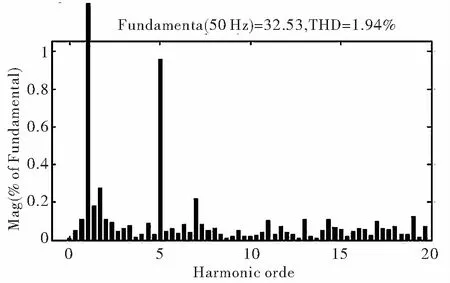
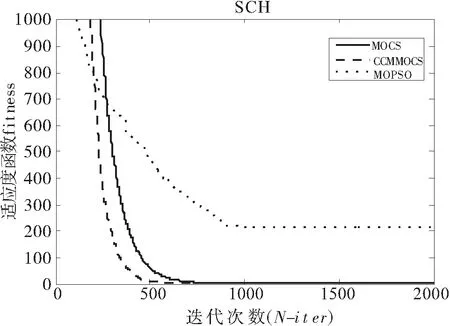
3 仿真结果及分析


4 结 论
