基于地理加权回归模型的亚热带地区乔木林生物量估算

王海宾 侯瑞萍 郑冬梅 高秀会 夏朝宗 彭道黎

(1.北京林业大学林学院， 北京 100083； 2.国家林业局调查规划设计院， 北京 100714； 3.中国空间科学技术研究院通信卫星事业部， 北京 100094)

0 引言

乔木林生物量作为森林生物量的主要组成部分，是森林可持续经营和生态环境监测的重要内容，在全球碳储量估测、碳储量循环以及碳收支平衡方面具有重要的地位和作用[1-3]。因此，准确地估测乔木林生物量对森林经营管理、生态环境保护建设以及全球碳储量循环具有重要意义[4-5]。

乔木林生物量的估测方法多以参数和非参数估测方法为主，其中参数方法以传统的回归分析为主[6]，主成分估计、岭估计、稳健估计、(偏)最小二乘估计等方法应用也较为广泛[7]，非参数方法包括k最近邻(k-nearest neighbor，k-NN)、人工神经网络(Artificial neural network，ANN)、支持向量机等方法的研究及应用也较为深入[8-10]。在现实的空间内，森林参数是存在空间依赖关系的，因此k-NN方法以及传统回归方法都被认为是非空间方法。然而，大多数地理现象是以空间依赖性为特征的，位于彼此相邻的地理空间中的点可能会显示出比彼此远离的点更加相似的特征[4]。此外，相关研究表明，空间分布的环境变量之间的关系可以在地理空间上有所不同[11]。

近年来在地统计学和空间建模领域，已发展了许多统计技术来模拟空间变量之间关系的空间变化。地理加权回归(Geographically weighted regression，GWR)作为探索空间异质性关系的强大工具之一，在地理学、生态学、气象学等学科得到了较为广泛的应用[11-15]。GWR方法是传统回归分析方法的扩展，进行局部而非全局的参数估计，它将数据的空间结构考虑到模型当中，使回归系数变成观测点地理位置的函数，以此来解决这种空间非平稳性问题[16]。笔者在之前的研究中[6]，采用了协同克里格(Co-kriging，COK)法对密云县森林蓄积量进行了估算并取得了较好的估测效果，这种方法在其他有关森林参数的研究中也显示了较好的预测精度[5,17]。相关的研究表明，在土壤属性空间预测领域[14-15]，GWR方法的预测精度优于COK方法，此外应用GWR方法进行大尺度范围的乔木林生物量(含地上和地下)的研究还不多，因此本文基于碳汇调查样地数据，采用协同克里格插值和地理加权回归方法对亚热带地区的乔木林生物量(含地上和地下部分)进行估测，并比较两者的估测精度，以期提高森林生物量的估测精度，为森林生物量模拟提供更好的数学模型算法。

1 研究材料

1.1 研究区概况

浙江省位于中国东南沿海，地理位置界于118°01′～123°10′E，27°06′～31°11′N之间，属于典型的亚热带季风气候区，季风显著、四季分明、雨热同期[18]。全省陆地面积1.02×105km2，地形较为复杂，西南部分以山地为主，平均海拔在100 m以上，中部多为500 m以下的丘陵，大小盆地相间分布；东北部为海拔10 m以下的冲积平原，河网密布；全省地势从西南向东北呈阶梯下降趋势。浙江省森林资源丰富，森林面积达到6.04×106hm2，林木蓄积量2.82×108m3，森林覆盖率59.34%，其中乔木林、经济林和竹林分别占森林总面积的68.90%、16.80%和14.30%。

1.2 数据准备

数据由国家林业局调查规划设计院碳汇计量监测中心提供，共计有247个，数据采集时间为2012年，样地调查数据分布见图1。样地形状为正方形，面积为0.067 hm2，样地主要包括针叶林、阔叶林、混交林等不同森林类型，属性因子包括树种、胸径(起测胸径为5 cm)、平均高、郁闭度、坡向、坡度、海拔、株数、年龄、乔木林地上生物量和乔木林地下生物量等因子。本研究用的因子有乔木林生物量(含地上和地下生物量)、郁闭度、平均高度、每公顷株数和海拔因子。

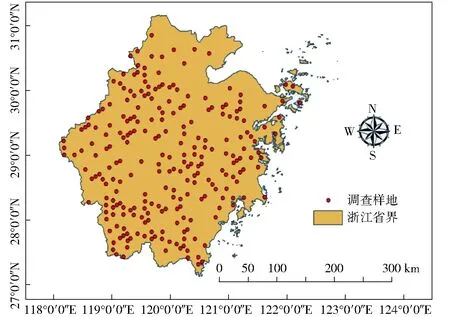
图1 研究区样地分布图Fig.1 Distribution of samples in study area

乔木林地上生物量采用样地蓄积量乘以生物量换算因子(Biomass expansion factor，BEF)计算获取，蓄积量直接采用已计算的样地蓄积量数据，生物量换算因子采用文献[18]提供的浙江省四大树种(组)的BEF，分别为杉木林0.745 3 t/m3、马尾松林0.883 9 t/m3、软阔类1.657 2 t/m3、硬阔类1.070 5 t/m3。将其他树种分别归并到软阔类和硬阔类树种(组)并采用相应的BEF进行生物量计算。乔木林地下生物量采用地上生物量乘以根茎比(立木地下生物量与地上生物量的比值)得到。根茎比数据同样由碳汇计量监测中心提供。将地上乔木林生物量和地下生物量相加即可得到样地内的乔木林总生物量(下文统称为乔木林生物量)，为便于计算，将乔木林生物量转换为每公顷生物量(t/hm2)。

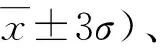
2 研究方法

2.1 空间自相关分析

对乔木林生物量进行空间自相关分析，检验研究数据是否随机分布，采用莫兰指数(Moran’sI)进行计算[2]

(1)

式中n——索引为i和j的样本总数

xi、xj——空间位置i和j的取值

wij——空间位置i和j的相邻关系

Moran’sI的取值范围在[-1,1]之间，小于0表示负相关，等于0表示不相关，大于0则表示正相关。本研究应用ArcGIS 10.1中的空间统计(Spatial statistics tools)中的空间自相关分析工具(Spatial autocorrelation)实现。

2.2 协同克里格插值

以往的研究表明[5-6,17]，协同克里格法较普通克里格法在变量的估测上具有较好的预测精度。它是利用2个或2个以上的变量，将其中一个作为主变量，剩余变量作为辅助变量，将主变量的自相关性和主辅变量的交互相关性结合起来进行无偏最优估计[6]，其公式为

(2)

其中

式中Z*(x0)——待估点处的变量估测值

λ1i、λ2i——主变量Z1和辅助变量Z2实测值的权重

m——辅助变量Z2的实测值数目

在应用协同克里格进行插值分析时，变异函数的选择至关重要。ArcGIS 10.1软件地统计分析模块提供了11种变异函数模型，包括指数模型(exponential)、高斯模型(Gaussian)、圆形模型(circular)、球状模型(spherical)、四球模型(tetraspherical)、五球模型(pentaspherical)、有理二次方程式(rational quadratic)、孔穴效应(Hole effect)、K-贝塞耳模型(K-Bessel)、J-贝塞耳模型(J-Bessel)和稳定模型(Stable)。本研究依据采用的碳汇调查数据，应用11种变异函数对乔木林生物量拟合，优选出最佳变异函数。变异函数的拟合效果采用交叉检验(Cross-Validation)来验证，通过交叉检验中的预测值和实测值进行分析，主要考虑决定系数(R2)和残差，R2越大，残差越小；其次是考虑变程和块金值，变程越大，块金值越小[6]。变异函数的拟合及验证过程可参照文献[6]。

2.3 地理加权回归

传统的回归(普通最小二乘)模型为

=0+1X1+2X2+…+qXq+ε

(3)

Xq——第q个变量的值

ε——模型残差，且服从N(0，σ2)分布

地理加权回归模型是基于普通全局回归模型的扩展，将空间影响考虑到模型构建中，以距离权重的形式加入到模型之中，故地理加权回归模型的基本形式可表现

=0(x,y)+1(x,y)X1+2(x,y)X2+…+
q(x,y)Xq+ε

(4)

式中x、y——空间样本的坐标

地理加权回归模型通过将回归置于一个移动的窗口(内核)中来解释关系的空间漂移。在此模型中，空间中每个点的回归参数都是不同的，可以通过使用空间距离权重函数的方法解决，其基本形式为

=(XTWiX)-1XTWiY

(5)

其中

Wi=diag(Wi0,Wi1,…,Win)

式中Wi——点i处空间权重对角线矩阵

由式(3)～(5)可知，解决地理加权回归模型的参数估计问题，关键在于空间权重矩阵，即如何选择空间权重函数，一般选择应用较为广泛的高斯函数法，其表达式为

Wij=exp(-(dij/b)2)

(6)

式中Wij——分配给位置i的观测值权重

dij——回归点i与数据点j之间的距离

b——带宽，为非负参数，表示权重与距离之间函数关系

在构建地理加权回归模型时，带宽的选择至关重要，带宽过小或过大，都会对模型的拟合精度产生影响，因此在模型拟合过程中需要对带宽进行优选。常用的带宽确定方法包括：交叉验证法(Cross-Validation，CV)、AIC准则(Akaike information criterion,AIC) 和贝叶斯信息准则(Bayesian information criterion，BIC)，本研究采用AIC方法来确定最佳带宽：当AIC值取得最小值时，即可获得最佳带宽及地理加权回归模型。AIC可以表示为

AIC=-2lnL+2k

(7)

式中k——未知参数的数量

L——似然函数

在AIC值最小时获得最优模型带宽。

ArcGIS 10.1软件中的地理加权回归工具提供了高斯核函数，常采用固定距离法和自适应法对权重函数进行校准，如研究数据分布是随机的，选择固定距离法较为适合，若数据分布不是随机的，则选择自适应法会得到更优的估算精度[4]。本研究同时采用2种方法对权重函数进行校准，用于优选带宽及构建GWR模型。

2.4 模型评价

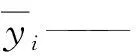
(8)

(9)

(10)

式中yi——蓄积量实测值

p——自变量个数

3 研究结果

3.1 描述性统计及相关性分析

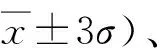
表1 变量描述性统计结果Tab.1 Statistical feature values of variables

借助ArcGIS 10.1计算了乔木林生物量的空间自相关性，采用莫兰指数进行评价，结果显示浙江省乔木林生物量的指数为0.071 6，呈空间正相关，并且在5%的显著性水平(p=0.016)下Z值为2.415(大于1.96)，高度显著，说明研究区内的乔木林生物量数据分布是非随机的。

应用SPSS 20.0软件对提取的变量进行Pearson相关性分析(表2)。由表2可知，乔木林生物量与郁闭度、平均高、每公顷株数和海拔之间存在极显著的相关关系，相关系数分别为0.609、0.576、0.592和0.372。受限于协同克里格插值辅助变量的个数，本研究选择相关性较高的郁闭度、平均高和每公顷株数3个因子参与协同克里格插值和GWR模型的构建。

表2 研究区变量间Pearson相关系数Tab.2 Pearson correlation matrix for variables of study area

注：** 在0.01 水平(双侧)上显著相关；*在0.05水平(双侧)上显著相关。

3.2 模型拟合

3.2.1协同克里格插值

以乔木林生物量为因变量，郁闭度、平均高和每公顷株数3个辅助因子参与协同克里格插值，对11种备选的变异函数进行拟合，筛选并确定最优变异函数(表3)。变异函数的评价标准为主要考虑R2和残差，再考虑块金值(C0)和变程，依据评价标准，综合考虑R2、残差、块金和变程，拟合效果最优的函数为有理二次方程式模型，因此本研究选择有理二次方程式作为协同克里格插值的最优变异函数。

表3 协同克里格法拟合的最优方差函数模型及参数Tab.3 Optimal variance function model and parameters fitted by COK

3.2.2地理加权回归模型

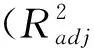
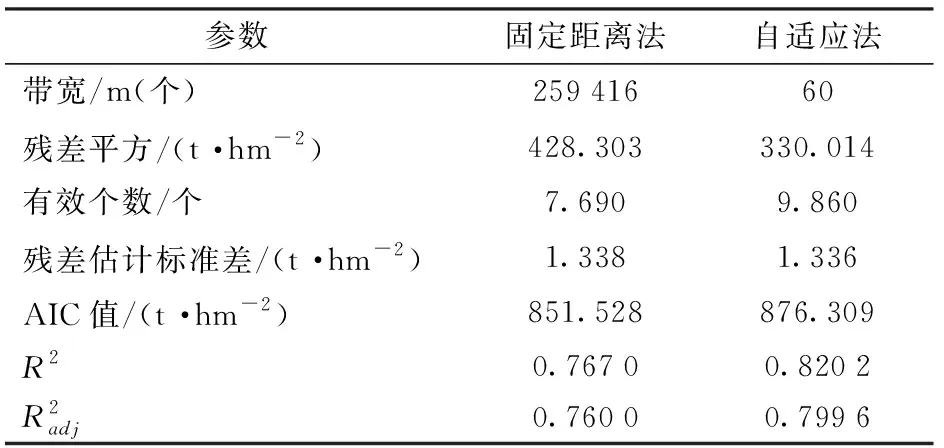
表4 GWR模型参数计算结果对比Tab.4 Parameter estimation results of GWR model

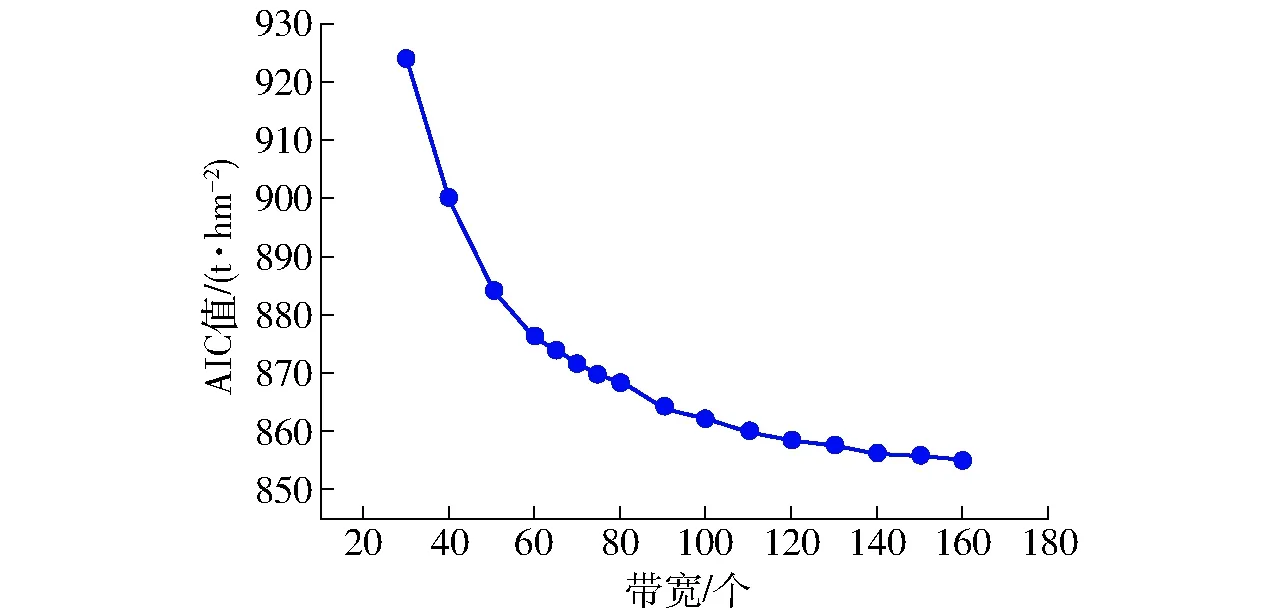
图2 GWR模型最佳带宽Fig.2 Selection of optimal bandwidth for GWR model

3.3 模型对比

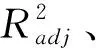
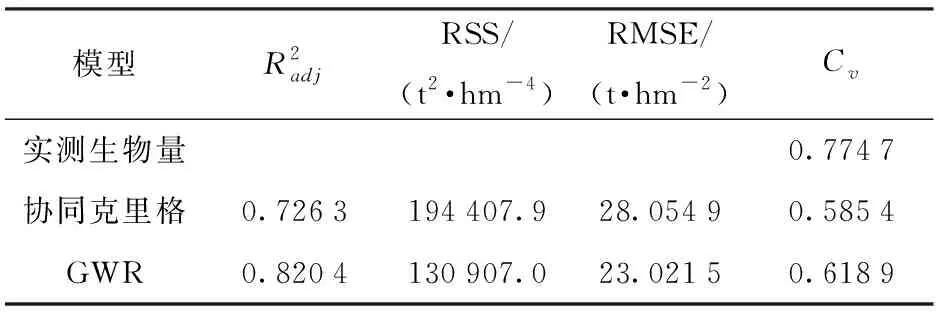
表5 乔木林生物量的协同克里格插值和GWR模型比较Tab.5 Comparison of COK interpolation and GWR model for biomass of arbor forest

绘制了GWR模型和协同克里格法的乔木林生物量预测偏差分布图(图3)，其中协同克里格法的预测偏差波段范围较大，为-69.99～66.74 t/hm2，GWR模型预测偏差范围为-53.58～46.87 t/hm2，可知GWR模型的残差分布区间小于协同克里格法，说明GWR模型比协同克里格法具有更好的拟合效果。

图3 两种模型的残差分布Fig.3 Distribution of residuals for two models

4 讨论

在前人的研究中，协同克里格法在森林生物量的估测上取得了较好的预测精度[5]，笔者先前使用了普通克里格和协同克里格法对密云区森林蓄积量进行估测，也取得了较好的预测精度[6]，说明协同克里格方法具有一定的应用优势。地理加权回归方法因其考虑了变量的空间异质性，可以进行局部回归估计，在一些研究中也取得了较好的预测效果[4,12-13]，因此本文选择协同克里格和地理加权回归方法对亚热带地区的乔木林生物量进行估算，并进行对比分析。

计算了乔木林生物量的空间自相关性，结果显示研究区内的乔木林生物量数据分布是非随机的，在GWR模型带宽的选择上，采用固定距离法和自适应法两种方法对权重函数进行校准，结果显示自适应法方法具有较好的预测精度，说明当乔木林生物量数据分布为非随机时，自适应法可以取得较好

的预测精度，这与前人研究结论相一致[4]。因此在应用地理加权回归方法估算变量时，可以先对变量数据进行空间自相关分析，检验数据是否随机分布，如果是随机分布的，可选用固定距离法对权重函数进行校准，若数据分布是非随机的，可采用自适应法对权重函数进行校准，可以有效地提高GWR模型的预测精度。

建模解释变量只选择了郁闭度、平均高和每公顷株数3个因子，而海拔因子也显示了极显著的相关关系，但受限于ArcGIS 10.1中协同克里格插值辅助变量个数的限制，未将海拔作为解释变量参与建模。在数据的测试分析过程中发现，将海拔因子作为GWR模型的解释变量参与建模，进一步提高了GWR模型的拟合精度，并对4个解释变量进行共线性诊断，结果显示4个解释变量不存在严重的共线性问题(方差膨胀因子均小于3)，因此在加入海拔因子后获得了更高的预测精度。在应用遥感影像估测森林生物量的研究中，影像波段衍生的植被指数及纹理特征因子间往往存在共线性问题，可能会影响甚至降低所构建模型的稳定性，而海拔因子属于第三维度的因子，往往与影像特征因子间的共线性较小，因此在以后的研究中，可考虑加入遥感影像和海拔因子，结合地理加权回归模型来进行乔木林生物量估测，检验其是否适用，提高GWR模型的预测精度。

5 结论

(1)基于碳汇专项调查样地数据提取的乔木林生物量、郁闭度、平均高、每公顷株数及海拔因子，进行皮尔森相关性分析和K-S检验，结果显示乔木林生物量与其余4个因子间均存在极显著关系，在经过数据转换处理后，各因子均呈现正态分布。

(2)选取固定距离法和自适应法两种方法对权重函数校准，结果显示自适应法要优于固定距离法，可以获得较好的预测精度。

1 刘晓梅，布仁仓，邓华卫，等.基于地统计学丰林自然保护区森林生物量估测及空间格局分析[J]. 生态学报,2011,31(16): 4783-4790.

LIU Xiaomei, BU Rencang, DENG Huawei, et al. Estimation and spatial pattern analysis of forest biomass in Fenglin Nature Reserve based on geostatistics[J]. Acta Ecologica Sinica, 2011, 31(16):4783-4790.(in Chinese)

2 毛学刚，王静文, 范文义. 基于遥感与地统计的森林生物量时空变异分析[J]. 北京林业大学学报,2016, 38(2): 10-19.

MAO Xuegang, WANG Jingwen, FAN Wenyi. Spatial and temporal variation of forest biomass based on remote sensing and geostatistics [J]. Journal of Beijing Forestry University, 2016, 38(2): 10-19. (in Chinese)

3 杨传强, 李士美. 2012年山东省乔木林碳储量研究[J]. 资源科学，2015, 37(8): 1661-1667.

YANG Chuanqiang, LI Shimei. Carbon storage of arboreal forests in 2012 in Shandong Province, China[J]. Resources Science, 2015, 37(8): 1661-1667. (in Chinese)

4 PROPASTIN P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data[J]. International Journal of Applied Earth Observation and Geoinformation, 2012, 18: 82-90.

5 贺鹏，张会儒，雷相东，等. 基于地统计学的森林地上生物量估计[J]. 林业科学，2013, 49(5)：101-109.

HE Peng, ZHANG Huiru, LEI Xiangdong, et al. Estimation of forest aboved-ground biomass based on geotatistics[J]. Scientia Silvae Sinicae, 2013, 49(5):101-109. (in Chinese)

6 王海宾, 彭道黎, 范应龙,等. 基于辅助信息的森林蓄积量空间模拟[J/OL]. 农业机械学报, 2016, 47(6): 283-289.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160637&flag=1&journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2016.06.037.

WANG Haibin, PENG Daoli, FAN Yinglong,et al. Spatial modeling of forest stock volume based on auxiliary information[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 283-289. (in Chinese)

7 涂云燕. 森林蓄积量遥感估测研究[D]. 北京：北京林业大学，2013.

TU Yunyan. The research of estimating forest volume based on remote sensing[D]. Beijing: Beijing Forestry University, 2013. (in Chinese)

8 范文义，张海玉，于颖，等. 三种森林生物量估测模型的比较分析[J]. 植物生态学报, 2011, 35(4): 402-410.

FAN Wenyi, ZHANG Haiyu, YU Ying, et al. Comparison of three models of forest biomass estimation[J].Chinese Journal of Plant Ecology, 2011,35(4):402-410. (in Chinese)

9 戚玉娇, 李凤日. 基于KNN方法的大兴安岭地区森林地上碳储量遥感估算[J]. 林业科学, 2015, 51(5): 46-55.

QI Yujiao, LI Fengri. Remote sensing estimation of aboveground forest carbon storage in Daxing’ an mountains based on KNN method[J]. Scientia Silvae Sinicae, 2015, 51(5): 46-55. (in Chinese)

10 郑刚, 彭世揆, 戎慧,等. 基于KNN方法的森林蓄积量遥感估计和反演概述[J]. 遥感技术与应用, 2010,25(3):430-437.

ZHENG Gang, PENG Shikui, RONG Hui, et al. A general introduction to estimation and retrieval of forest volume with remote sensing based on KNN[J]. Remote Sensing Technology & Application, 2010, 25(3):430-437. (in Chinese)

11 FOTHERINGHAM A S, BRUNSDON C, CHARLTON M. Geographically weighted regression: the analysis of spatially varying relationships[M]. Chester UK: International Union of Crystallography, 2002.

12 WANG Quan, NI Jian, TENHUNEN John. Application of a geographically-weighted regression analysis to estimate net primary production of Chinese forest ecosystems[J]. Global Ecology and Biogeography,2005, 14: 379-393.

13 郭含茹. 基于地理加权回归的区域森林碳储量估计[D]. 杭州：浙江农林大学，2015.

GUO Hanru. Geographically weighted regression based estimation of regional forest carbon storage[D]. Hangzhou: Zhejiang A&F University, 2015. (in Chinese)

14 郭龙, 张海涛, 陈家赢,等. 基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较[J].土壤学报, 2012, 49(5): 1037-1042.

GUO Long, ZHANG Haitao, CHEN Jiaying, et al. Comparison between co-Kriging model and geographically weighted regression model in spatial prediction of soil attributes[J]. Acta Pedologica Sinia, 2012, 49(5): 1037-1042. (in Chinese)

15 袁玉芸, 瓦哈甫·哈力克, 关靖云, 等. 基于GWR模型的于田绿洲土壤表层盐分空间分异及其影响因子[J]. 应用生态学报, 2016,27(10): 3273-3282.

YUAN Yuyun, HALIKE Waha, GUAN Jingyun, et al. Spatial differentiation and impact factors of Yutian Oasis’s soil surface salt based on GWR model[J]. Chinese Journal of Applied Ecology, 2016, 27(10): 3273-3282. (in Chinese)

16 戚玉娇. 大兴安岭森林地上碳储量遥感估算与分析[D]. 哈尔滨：东北林业大学, 2014.

QI Yujiao. Estimation of forest above ground carbon storage using remote sensing in Daxing’ anmountains[D]. Harbin: Northeast Forestry University, 2014. (in Chinese)

17 MENG Q, CIESZEWSKI C, MADDEN M. Large area forest inventory using Landsat ETM+: a geostatistical approach[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2009, 64(1):27-36.

18 沈楚楚. 浙江省主要树种(组)生物量转换因子研究[D]. 杭州：浙江农林大学, 2013.

SHEN Chuchu. The research on biomass expansion factors of the dominant tree species in Zhejiang Province[D]. Hangzhou: Zhejiang A&F University, 2013. (in Chinese)

19 DU H, ZHOU G, FAN W, et al. Spatial heterogeneity and carbon contribution of aboveground biomass of moso bamboo by using geostatistical theory[J]. Plant Ecology, 2010, 207(1):131-139.

20 KUMAR S, LAL R, LIU D. A geographically weighted regression Kriging approach for mapping soil organic carbon stock[J]. Geoderma, 2012, 189-190(6):627-634.