二次型在代数学中的应用

张立新

(鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

二次型是高等代数中一个比较独立而重要内容，它的理论知识不仅在中学数学，而且在大学数学中都有着广泛的应用.通过二次型应用的研究,可以有效地提高学生的数学应用意识.

1 二次型的相关理论

数域P上n元二次齐次多项式

其中，aij=aji,AT=A)

称为数域P上二次型.

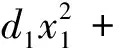
化简二次型为标准形的基本方法有3种：配方法、合同变换法、正交变换法.

二次型的标准形不唯一，规范形唯一.

设

是n元实二次型(A为实对称矩阵)，如果对任意不全为零的实数c1,c2,…,cn都有f(c1,c2,…,cn)>0则称为f为正定二次型.如果对任意不全为零的实数c1,c2,…,cn都有f(c1,c2,…,cn)≥0则称为f为半正定二次型.如果对任意不全为零的实数c1,c2,…,cn都有f(c1,c2,…,cn)<0则称为f为负定二次型.如果对任意不全为零的实数c1,c2,…,cn都有f(c1,c2,…,cn)0则称为f为半负定二次型.

(1)在实二次型f(x1,x2,…,xn)的规范形中，正平方项的个数p称为f(x1,x2,…,xn)的正惯性指数；负平方项的个数r-p称为f(x1,x2,…,xn)的负惯性指数；它们的差称为f(x1,x2,…,xn)的符号差.其中，r为f(x1,x2,…,xn)的秩[2].

(2)一个实二次型可以分解成两个实系数的一次齐次多项式的乘积的充要条件是它的秩等于2和符号差等于0，或者它的秩等于1[3].

(3)一个n元实二次型

(A是实对称矩阵),

(4)正定二次型与正定矩阵的判定：

①n元实二次型

(A是实对称矩阵)

正定的充分必要条件是它的正惯性指数为n.

②n级实对称矩阵A是正定的充分必要条件是A与单位矩阵E合同.

③n级实对称矩阵A是正定的充分必要条件是存在n级实可逆矩阵C，使A=C′C.

④n级实对称矩阵A是正定的充分必要条件是A的顺序主子式都大于零.

⑤n级实对称矩阵A是正定的充分必要条件是A的特征值都大于零.

(5)半正定二次型与半正定矩阵的判定：

①n元实二次型

(A是实对称矩阵)

半正定的充分必要条件是它的正惯性指数与秩相等.

③n级实对称矩阵A是半正定的充分必要条件是存在n级实矩阵C，使A=C′C.

④n级实对称矩阵A是半正定的充分必要条件是A的主子式都大于零.

⑤n级实对称矩阵A是半正定的充分必要条件是A的特征值都非负.

2 二次型的应用

2.1 二次型在初等数学中的应用

例1对任意不全为0的实数x,y,z，证明：

证明上述问题等价于求

f(x,y,z)=x2+y2+2z2-3axy-ayz-azx≥0

恒成立的a的取值范围.

得A的各阶主子式分别为

则

解得

在

x2+y2+2z2-3axy-ayz-azx≥0

中，分别取

得

从而有

例2已知实数x,y满足x2+y2=1，求

f(x,y)=x2-2xy+2y2

的最小值及最大值.

解令

f(x,y)=x2-2xy+2y2=X′AX，

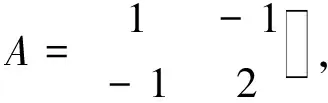
由

因此，特征值：

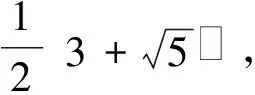
例3判断下列多项式在R上能否分解？若能，分解之.

解令

则

f(x1,x2)=g(x1,x2,1).

利用配方法，经

将

也能分解，

2.2 二次型在高等数学中的应用

例4方程

表示何曲面？

解

则方程改写为：

X′AX+B′X+3=0.

A的特征多项式为

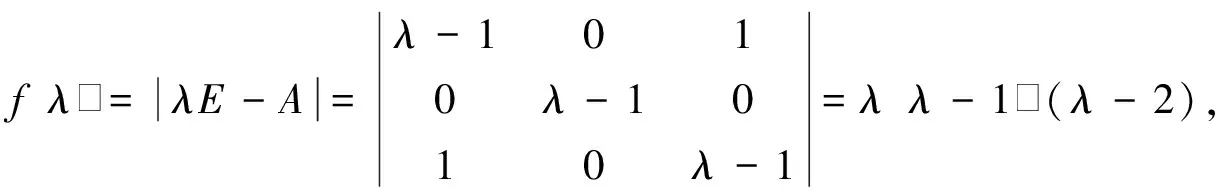
A的特征值1,2,0所对应的特征向量分别为(0,1,0)′,(1,0,-1)′,(1,0,1)′.

取正交矩阵

及正交变换X=TY代入方程得：

Y′T′ATY+B′TY+3=0，

整理得

配方得到

(y1-1,)2+2(y2-1)2=6y3.

令

由此可知，方程表示的曲面为椭圆抛物面.

例5已知A是n级正定矩阵，Y,X∈Rn,b∈R，求f(x)=X′AX+2Y′X+b的极值.

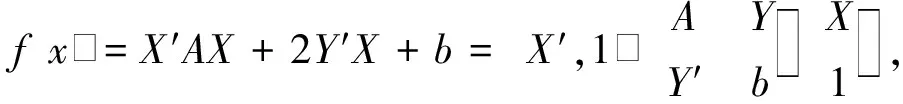
所以

(X′+Y′A-1)A(X+A-1Y)+b-Y′A-1Y=

(X+A-1Y)′A(X+A-1Y)+b-Y′A-1Y.

因为A是正定矩阵，所以

(X+A-1Y)′A(X+A-1Y)≥0，

故当X=-A-1Y时，f(x)的极小值为b-Y′A-1Y.

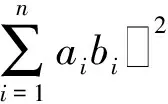
证明令

则B′B正定矩阵，从而|B′B|≥0

≥0，

即柯西不等式成立.

2.3 研究生考试中的二次型问题

例7若A是n级实对称阵，证明A半正定的充要条件是对任何μ>0,B=μE+A正定.(1993年考研试题)

证明A是n级实对称阵,从而存在正交阵T，使

其中，λ1,…,λn为A的全部实特征值.

先证必要性，若A半正定，则

λi≥0(i=1,2,…,n)，

则B的全部实特征值

μ+λi>0(i=1,2,…,n)，B′=B∈Rn×n，

所以B为正定.

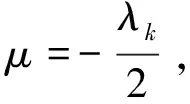
则μ>0，但

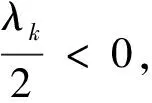
例8设n元实二次型

f(x1,x2,…,xn)=(x1+a1x2)2+(x2+a2x3)2+…+(xn-1+an-1xn)2+(xn+anx1)2,

其中,ai(i=1,2,…,n)为实数，试问：当a1,a2,…,an满足何种条件时，二次型f(x1,x2,…,xn)为正定二次型.(2000年考研试题)

解由题设条件知，对于任意的x1,x2,…,xn,有f(x1,x2,…,xn)≥0,

其中,等号成立当且仅当

此方程组仅有零解的充要条件是其系数行列式不为零，即

所以，当1+(-1)n+1a1a2…an≠0时，对于任意的不全为零的x1,x2,…,xn,有f(x1,x2,…,xn)≥0，即当a1a2…an≠(-1)n时，二次型f(x1,x2,…,xn)为正定二次型.

3 一点思考

本文从3个方面(即初等数学、高等数学、考研)研究了二次型的应用.其实二次型不仅在数学的各个方面有着应用，而且在物理、力学、工程技术中也有着广泛的应用.虽然在高等代数教材中没有介绍它的应用，但在高等教育改革的今天，为了更好地培养学生的数学应用意识，教师在授课之余应有意识地渗透二次型的应用.也就是说：教师在授课时应重视学生数学应用意识的培养[4].

要培养学生的数学应用意识，教师要有较强的数学应用意识与应用能力[5].为此，教师应刻苦钻研，在数学教学过程中，少一些纯粹的数学问题，多一些实际的数学应用，潜移默化地感染学生，使学生逐渐形成数学应用意识.

要培养学生的数学应用意识，教师要善于创设情境，改革评价形式，引导学生学以致用.学生在应用数学知识的同时，也巩固了数学知识.长此以往，学生的数学兴趣得到激发，数学素养得到锤炼，数学思想得到升华[6]，从而有效地培养了学生的数学应用意识与应用能力.

[1] 王萼芳，石生明.高等代数[M].北京：高等教育出版社，2003.

[2] 姚慕生.高等代数学[M].上海：复旦大学出版社，2003.

[3] 张禾瑞，郝鈵新.高等代数[M].北京：高等教育出版社，2001.

[4] 刘维.浅谈数学应用意识的培养[J].学术论坛,2011(11):49-50.

[5] 张文海.浅议高中生数学应用意识的培养[J].数学教学研究，2017(6)：17-19.

[6] 田卫东.加强教材习题的研究，让学生的思维展翅飞翔——对一道课本习题的探究与思考[J].数学教学研究，2017(12)：38-42.