基于人工势场和量子遗传算法的移动机器人路径规划方法

侯 翔(四川文理学院智能制造学院 四川 达州 635000)

0 引 言

移动机器人是一种在特定空间内自行组织、运行与路径规划的智能机器人，其中路径规划是机器人学和智能技术中重要的部分[1]。目前，移动机器人路径规划的主要方法包括：滚动路径规划法[2]、人工势场法[3-4]、遗传算法[5]等。Khatib最先提出人工势场(Artificial Potential Field)理论，通过把机器人所处的环境看作是理想化的人造力场，来解决机器人在环境中的路径规划问题。另外，有学者提出通过栅格方法[6]来代表地图中的不同地形，从而实现了在对全局区域上的机器人路径规划，并取得较好的效果。随着遗传算法理论的提出，这种通过模拟自然界中物种进化的方式来搜索最优解的方法被引入到机器人路径规划的问题上，但是该理论存在收敛效率低下的弊端。随着量子力学理论[7]的不断发展，利用量子的重叠与牵连原理使得量子计算具有很强的功能，但它具有容易陷入局部最优的缺点。目前的研究无法解决移动机器人在前往障碍物附近的目标时的路径规划的问题。

本文在现有人工势场的基础上进行改进，提出一种用于解决机器人在前往障碍物附近的目标时的路径不可达的问题。本文方法包括两个方面：首先，在设定的环境内通过引入指数因子的形式来优化势场函数表达式，从而平衡障碍物的斥力、消除了奇异值点，使机器人可以正确地到达目标点。针对得到的路径轨迹，利用量子遗传算法对最优或次优的路径规划进行选择。通过仿真实验表明，该方法解决了障碍物附近目标不可达问题，有效地提高了路径规划的性能。

1 基于人工势场的路径规划

1.1 传统的人工势场介绍

人工势场将机器人视为质点，存在于该势场的机器人同时受到斥力和引力的作用[8]。当机器人距离障碍物越近时，受到的斥力就越大；反之，如果机器人距离障碍物较远时，机器人与目标之间的引力起主导作用，并且该引力大小与距离呈正相关。参考文献[9]，将人工势场表示为如下的形式：

Utotal=Urep+Uatt

(1)

式中:Utotal、Urep和Uatt分别为总势场、引力场和斥力场。转化为力的形式如下：

Ftotal=Frep+Fatt

(2)

式中：Ftotal是合力；Frep是斥力；Fatt是引力，式(2)中：

(3)

(4)

根据人工势场的理论，障碍物和目标点对机器人分别表现出斥力与引力的作用。如果障碍物与机器人之间的距离大于ρ0，引力场的作用表现为零；如果障碍物与目标点距离很小时，在机器人逐渐靠近目标的过程中，表现出来的引力则会逐渐变小，斥力则会逐渐变大。这个时候，如果机器人可能出现在障碍物附近徘徊的情况，而无法到达目标。根据势场理论可知，随着障碍物数目的增大，存在这种不可达的概率也越大。

1.2 改进的人工势场

经过以上分析可知，传统的势场法具有对于处于障碍物附近的目标，存在不可达的情况[10-11]，这是因为该障碍物附件的目标点不能满足式(1)的最小值。为了解决该问题，本文定义了如下函数表达式：

(5)

式中：ρ(Xr,Xgoal)表示目标点和机器人两者间的距离大小，ρ(Xr,Xobs)表示ρ(Xr,Xgoal)的最小值。如果出现机器人无法到达目标时，通过式(5)可获得改进后斥力的表示形式，如公式所示：

(6)

式中：

(7)

(8)

单位向量a的方向为由障碍物指向机器人，单位向量b的方向与向量a相反。当n=0时，由式(5)变化为如下函数：

(9)

改进的人工势场通过引入目标点和机器人两者间距离上的指数形式，对传统的势场函数表达式进行改进，从而对机器人无法达到目标情况下的障碍物的斥力进行描述，消除机器人在路径规划上的奇异点。改进的人工势场解决了机器人在路径规划上不可达的问题，但是通过该方法找到的路径规划有时候不只一条，那么应该选择哪条路径进行移动，这时候需要对多条可达路径进行寻优。

2 基于量子遗传算法的路径寻优

针对改进的人工势场得到多条路径规划后，下面通过量子遗传算法对多条可达的路径进行寻优。这一节在传统的量子遗传算法的基础上进行了扩展，建立了适合于本文场景下的寻优方法。首先对量子遗传算法中的量子比特编码进行介绍，然后提出了通过对量子门中的旋转操作进行调整来缩短算法收敛时间的方法，最后通过路径代价和安全性作为评价标准，建立路径规划上的适应度函数，从而进行路径的寻优。

2.1 量子比特编码介绍

根据量子遗传算法理论，基本的信息元素以量子位的形式表示，量子位是进行量子化处理的基本单元。该单位的所处形态用0或1来代表，形式如公式所示：

|φ〉=α|0〉+β|1〉

(10)

式中：α、β代表相应状态出现概率的两个复数，且：

(11)

2.2 对量子遗传算法的改进

根据量子计算可知，已知的量子态是由量子门进行矩阵转换的形式来完成转换[12]。量子门的对应旋转角表示了染色体的变异处理，从而有效地缩短了运算的收敛时间。下面对量子门中的旋转操作进行调整：

(12)

则

(13)

θi=s(αi,βi)Δθi

(14)

θi=s(αi,βi)与Δθi对应表示旋转操作的指向与角度数值，后者的值域为[0.1π,0.005π]。

本文通过调整旋转角度，从自适应的角度对传统的量子遗传算法进行了改进，见表1。此策略方法依据个体此时对应的测量值和目标值的适应度，查看满足的条件来确定下一步的操作，测量值和目标值分别用f(xi)与f(bi)来表示。若满足关系式(f(xi)-f(bi))/f(bi)小于给定的阈值时，采取降低δ值的方法来提高收敛速度，缩短运算时间；否则，就应采用增大δ值的方法，避免局部寻优现象的出现。

表1 旋转角调整策略

2.3 构建适应度函数

对于改进的人工势场得到的多条路径规划来说，路径代价与安全性是评价路径优劣的两个重要标准。在路径寻优时，本文根据下述函数作为适应度函数：

(15)

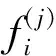
(16)

式中：i与j分别为染色体与路径点的次序数，β、γ表示调整系数值大小，其中β+γ=1，两者之间数值的选取表示了路径正确性与安全性之间的权衡，一般情况下将β的值设置为大于γ，并根据系统对安全性的需求来提高对γ的赋值。

(17)

式中：L表示路径点与目标点之间的线段距离数值。由u值大小来确定对应路径选择的合理与否。

(18)

式中：q表示路径中存在的障碍物总数目。式(18)的数值表示了对应路径点上的安全性。

(19)

式(19)的数值表示障碍影响参数，数值越大说明障碍对机器人的路径的阻碍越大。

2.4 路径规划寻优过程

根据以上提出的改进的量子遗传算法和适应度函数，这一节介绍基于量子遗传算法对改进的人工势场中得到的多个路径规划进行寻优的具体过程。具体步骤为：

步骤1利用改进的人工势场进行初始化种群：

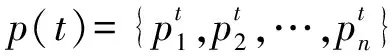
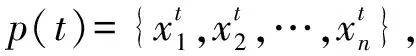
步骤3用上述的评价函数，准确评价种群内的全部个体。在获取最优解之后，取此时的目标值与之对比。若出现目标值小于最优解的情况，取此时的最优解当做下次迭代操作时的目标值大小，重复进行上述操作；若出现目标值大于最优解的情况，进行下次迭代时，目标值依然恒定。

步骤4依据自适应原则，使用旋转门调整方法，对P(t)进行下一轮的操作。

步骤5进行停止条件判断，如果条件实现，停止运算，输出结果，如果条件未满足，继续计算。

步骤6取t=t+1，继续转入步骤2，继续计算。

3 仿真实验

针对本文提出的基于改进的人工势场进行移动机器人的路径规划方法，本节从两个方面进行实验验证分析：1) 对解决机器人在前往障碍物附近的目标时的路径不可达问题上的有效性；2) 通过与量子遗传算法、遗传算法进行对比，验证本文改进的算法在机器人路径规划寻优上的优势。

实验一：当目标机器人在存在障碍物的区域内行进时，将会出现在附件徘徊的情况，无法达到目标。这种状况下，是由于传统的人工势场本身的局限性，致使机器人出现不能到达障碍物附件的目标的问题，如图1所示。

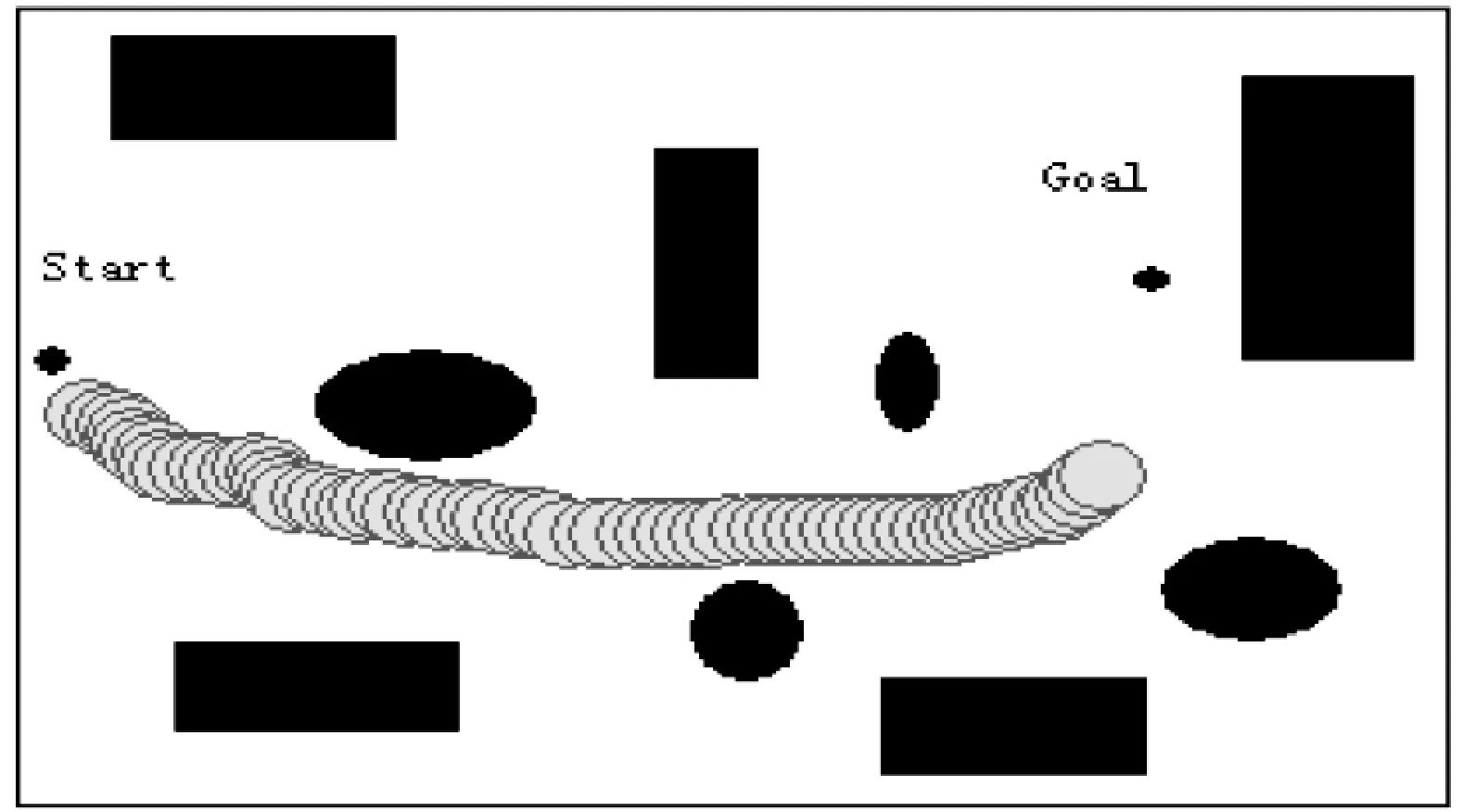
图1 传统人工势场的不可达情况

当人工势场经过改进之后，区域计算时引入了ρ(Xr,Xgoal)因子参数，并且设定n=2。图2表示通过改进后人工势场进行路径规划的效果图。从图中可以看出，移动机器人能够顺利到达目标区域，从而说明改进的人工势场可以有效解决移动机器人对于障碍物附件目标的不可达的问题。

图2 势场改进后的效果图

实验二：对于基于改进的人工势场得到的路径规划，将本文改进的量子遗传算法分别与量子遗传算法、遗传算法进行对比。分别从算法性能和优化能力两个方面进行实验。

其中，三种算法在解决移动机器人的路径规划方案上的优化问题上，具体表现出来的性能详见表2。

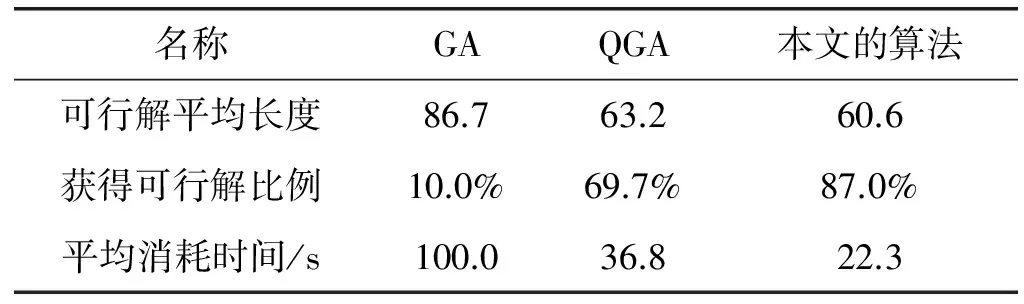
表2 计算性能比较

另外，对于给定的规划路径，三种不同算法对于路径的优化能力见图3，其中，虚线代表GA的适应度，实线代表QGA的适应度，点虚线代表本文算法的适应度。可以看出，本文提出的改进的算法具有较高的寻优速度和能力，一般在20代左右收敛到最优解附近。

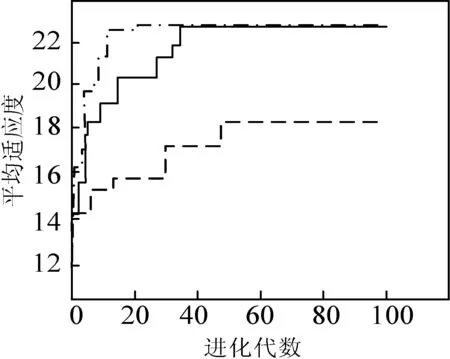
图3 三种算法的优化能力比较

综上所述，本文提出的改进的量子遗传算法一般的量子遗传算法和遗传算法比较可知，本文方法在寻找改进人工势场上的机器人路径规划时，具有较好的运算性能和优化能力。

4 结 语

对于移动机器人的路径规划问题，本文在全面分析传统的人工势场法具备的缺点和劣势的基础上，提出了改进的人工势场来平衡障碍物的斥力、消除了奇异值点，使机器人可以到达障碍物附近的目标点。然后针对改进的人工势场得到的多个路径规划，通过改进的量子遗传算法从路径代价与安全性两方面对路径进行寻优。经过实验可知，该方法具备有效性和可行性。

[1] 张浩杰, 龚建伟, 姜岩, 等. 基于变维度状态空间的增量启发式路径规划方法研究[J]. 自动化学报, 2013,39(10):1602- 1610.

[2] 陆萍, 董虎胜, 钟宝江. 协同进化粒子群滚动优化的机器人路径规划[J]. 计算机测量与控制, 2013, 21(11): 3128- 3130.

[3] 张殿富, 刘福. 基于人工势场法的路径规划方法研究及展望[J]. 机器人, 2013, 35(6): 88- 95.

[4] Han D, Nie H, Chen J, et al. Dynamic obstacle avoidance for manipulators using distance calculation and discrete detection[J]. Robotics and Computer-Integrated Manufacturing, 2018, 49: 98- 104.

[5] Roberge V, Tarbouchi M, Labonté G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning[J]. Industrial Informatics, IEEE Transactions on, 2013, 9(1): 132- 141.

[6] 欧阳鑫玉, 杨曙光. 基于势场栅格法的移动机器人避障路径规划[J]. 控制工程, 2014, 21(1): 134- 137.

[7] He B, Liu G, Yan J, et al. A UAV Route Planning Method Based on Voronoi Diagram and Quantum Genetic Algorithm[J]. Electronics Optics & Control, 2013, 11(2): 194- 203.

[8] 高强, 宋雨, 吕东澔, 等. 多移动机器人路径规划仿真研究[J]. 计算机仿真, 2014, 31(7): 325- 329.

[9] Li G, Tamura Y, Yamashita A, et al. Effective improved artificial potential field-based regression search method for autonomous mobile robot path planning[J]. International Journal of Mechatronics and Automation, 2013, 3(3): 141- 170.

[10] 吴慧超, 罗元, 周前能, 等. 时效优先的轮式机器人编队避障策略[J]. 信息与控制, 2017, 46(2): 211- 217.

[11] 潘桂彬, 潘丰, 刘国栋. 基于改进混合蛙跳算法的移动机器人路径规划[J]. 计算机应用, 2014, 34(10): 2850- 2853.

[12] Du K L, Swamy M N S. Bacterial Foraging Algorithm[M]//Search and Optimization by Metaheuristics. Springer International Publishing, 2016: 217- 225.