非NHPP类SRGM加权组合预测精度的实验分析

崔 霞 高建华(华东师范大学计算机科学与软件工程系 上海 0006)(上海师范大学计算机科学与技术系 上海 0034)

0 引 言

软件可靠性增长模型SRGM[1]的主要目的在于描述软件在开发设计阶段，软件中的错误不断被发现和纠正，可靠性不断增长的过程，并用于估计软件的可靠性和残余错误数等。非齐次泊松过程NHPP模型是SRGM中应用最广泛的一类。

文献[2-3]并未指出没有统计框架的非NHPP类SRGM基于三种加权平均，能否达到提升模型预测精度的目的、提升的幅度如何等。本文基于一种实数编码GA算法[4]，针对不同的时间间隔故障数据集，求取最优的非NHPP模型及其组合加权系数。运用均方误差函数，比较组合前后预测精度的差异。实验结果表明，虽然在非NHPP类SRGM中尚未建立某种统一框架，但基于实数编码GA算法的加权平均方法依然可以在某种程度上提高SRGM的预测能力。模型预测精度的提高幅度也较为明显。

1 非NHPP类SRGM的加权组合

NHPP类SRGM的统一框架性质是加权组合后可靠性预测精度提高的理论基础[2-3,5-10]。本节将对没有相似统一框架特性的其他非NHPP类SRGM考察加权组合的效果和特性。

1.1 候选非NHPP类SRGM

除了NHPP类SRGM 以外，在软件可靠性工程中应用较多的还有Markov过程模型(例如，Jelinski-Moranda模型，简称J-M模型；Musa执行时间模型，简称Musa模型)、贝叶斯模型(例如，Littlewood-Verrall模型，简称L-V模型；Littlewood’s Bayesian Debugging Model模型，简称LDM模型)等[1]。本文选择J-M模型、Musa模型、L-V模型和LDM模型作为候选模型。其主要原因：一方面是上述4种模型具有一定的代表性；另一方面该4种模型都使用失效时间间隔TBF(Time between Failure)数据作为模型实施的要求数据。关于该4种SRGM的具体描述如表1所示。

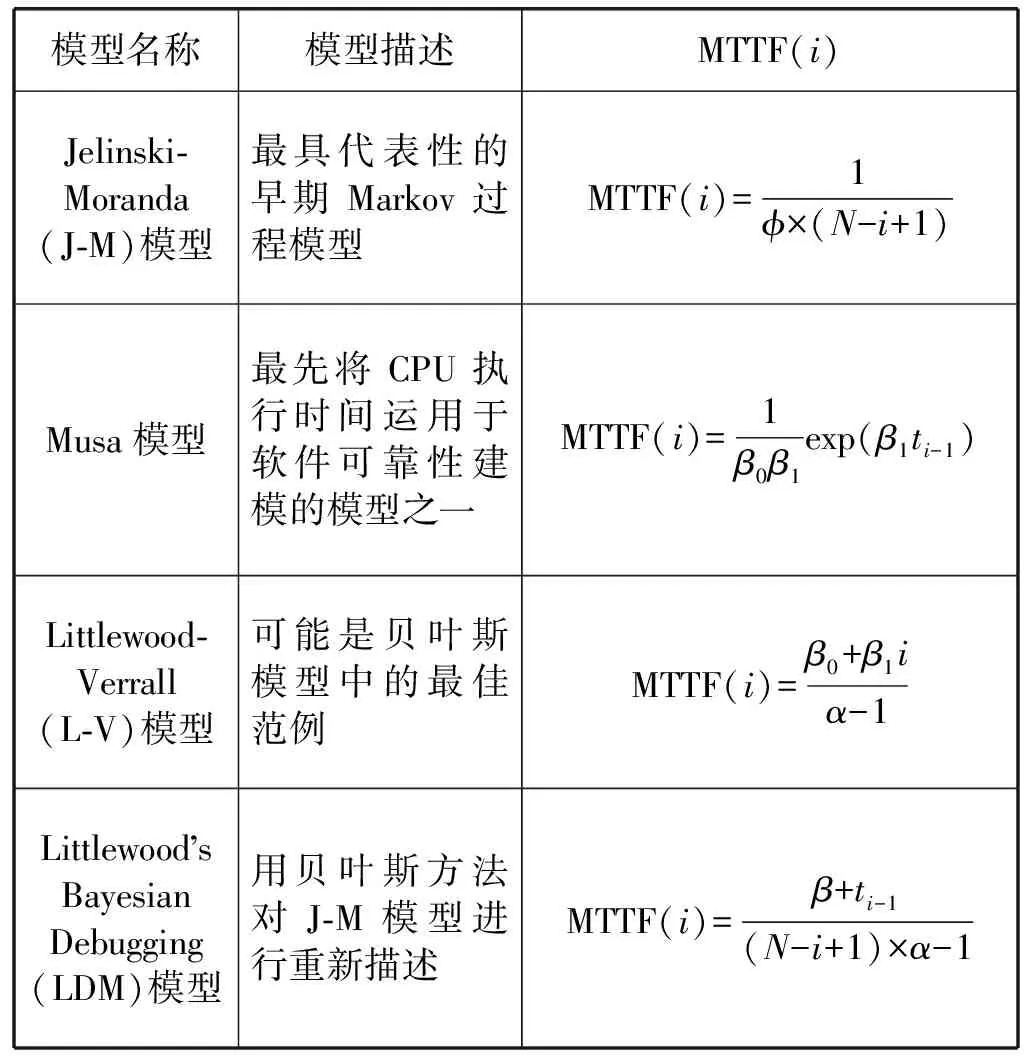
表1 候选SRGM的具体描述

1.2 故障数据集来源

本文引用文献[1]中的失效时间间隔数据集进行实验研究，如表2所示。其中值得关注的是，表2中的数据集S2与文献[1]中的数据集DS9是同一测试和调试过程中所产生的失效计数数据和失效时间间隔数据。它们所反映的软件可靠性增长的过程是相同的。

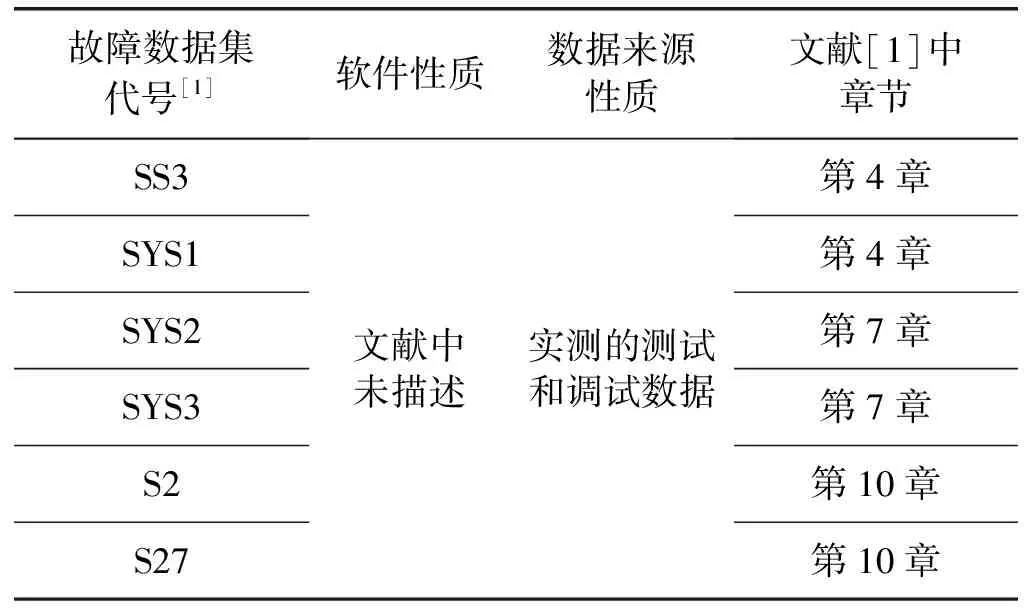
表2 故障数据集的特征

2 模型参数寻优

基于实数编码GA算法，针对表2中的6个故障数据集求解4种候选模型的最优参数。表3、表4是以式(1)为适应度函数求解的结果。

(1)

式中：mc()对应失效计数数据；m()对应待寻优的SRGM的均值函数MVF(Mean value function)。

从表3、表4可见，上述6个数据集下4个候选模型的MSE值都较大，除了模型的预测能力差异之外，还是因为实测的失效时间间隔数据都是以秒或者毫秒为单位的缘故。LDM模型是用贝叶斯方法对J-M模型重新描述，从最优化的结果可以看到，最优参数下的J-M模型和LDM模型都全局收敛到了相近的MSE值。

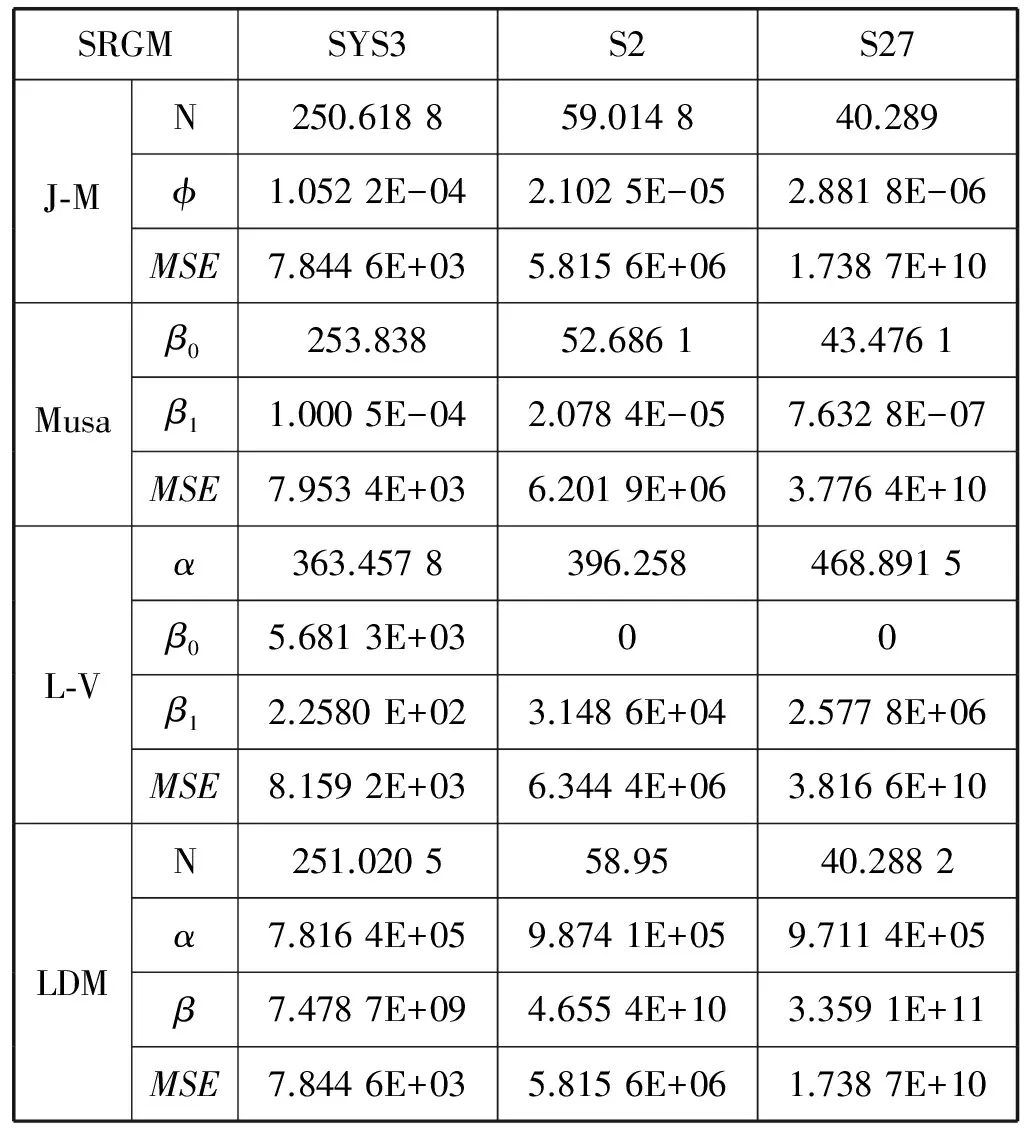
表4 基于MSE适应度函数的模型最优参数(下)

3 加权组合

基于实数GA算法，运算得到4种候选非NHPP类SRGM的算术加权平均组合、几何加权平均组合和调和加权平均组合的结果分别如表5、表6和表7所示。

表5 非NHPP类SRGM的算术加权平均组合

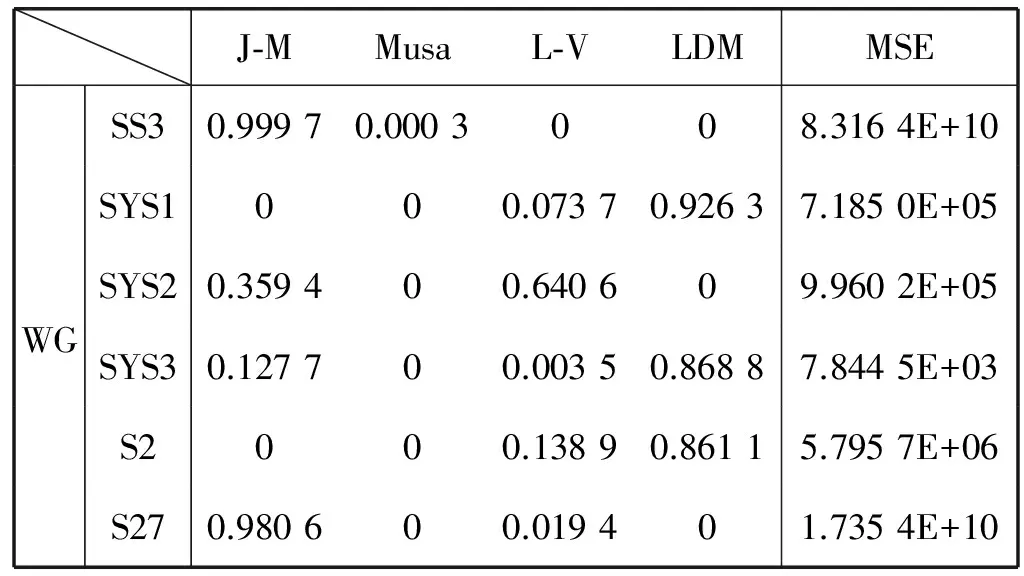
表6 非NHPP类SRGM的几何加权平均组合

表7 非NHPP类SRGM的调和加权平均组合

由表5-表7的组合系数求解结果中可以看出三种加权平均组合的加权系数之间具有明显的一致性。6个故障数据集中仅S27出现了组合模型的不同和加权系数的较大差异以外，其余5个数据集的组合模型完全一致，加权系数大小相近。

4 预测精度比较

已知故障数据集[1]S2与DS9是同一测试和调试过程中所产生的失效计数数据和失效时间间隔数据。本文以故障数据集S2和DS9为对象，比较NHPP类候选SRGM和非NHPP类候选SRGM的可靠性预测能力的差异，本文建立以下函数：

(2)

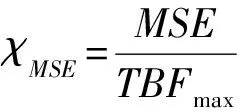
(3)

式中：参数FCmax表示同一故障集中最大失效计数；参数TBFmax表示同一故障数据集中最大的失效时间间隔。

χMSE函数值越小，说明模型的可靠性预测能力越强，预测精度越高。从表8的比较结果中可见，NHPP类SRGM的预测能力较强，这也从实验的角度说明了NHPP类SRGM在软件可靠性工程中得到广泛运用的原因。

表8 可靠性预测能力比较结果

5 结 语

本文随机引用了6个失效时间间隔数据集，分别用实验的方法验证了4个典型的非NHPP类(2个Markov类和2个贝叶斯)SRGM的可靠性预测能力和加权组合后的预测精度的变化。实验结果表明，虽然非NHPP类SRGM没有类似的统一框架，而且加权组合后的可靠性预测精度提高幅度也较为明显。由此可见，算术加权、几何加权和调和加权平均的方法对提高SRGM的预测精度具有一定的作用。从表7的比较结果中可见，NHPP类SRGM的预测能力较强，这也从实验的角度说明了NHPP类SRGM在软件可靠性工程中得到广泛运用的原因。

[1] Lyu M R.Handbook of Software Reliability Engineering[M].New York,NY,USA:McGraw-Hill,1996.

[2] Huang C Y,Lyu M R,Kuo S Y.A Unified scheme of some nonhomogenous poisson process models for software reliability estimation[J].IEEE Transactions on Software Engineering,2003,29(3):261- 269.

[3] Hsu C J,Huang C Y.Optimal Weighted Combinational Models for Software Reliability Estimation and Analysis[J].IEEE Transactions on Reliability,2014,63(3):731- 749.

[4] 崔霞,高建华.实物编码GA算法NHPP类SRGM预测能力的实验研究[J].小型微型计算机系统,2017,38(10):2336- 2340.

[5] Liu Y,Li D,Wang L,et al.A general modeling and analysis framework for software fault detection and correction process[J].Software Testing Verification & Reliability,2016,26(5):351- 365.

[6] Ullah N,Morisio M,Vetro A.Selecting the best reliability model to predict residual defects in open source software[J].IEEE Computer,2015,48(6):50- 58.

[7] Zeephongsekul P,Fiondella J L,Nagaraju V.Maximum-likelihood estimation of parameters of NHPP software reliability models using expectation conditional maximization algorithm[J].IEEE Transactions on Reliability,2016,65(3):1571- 1583.

[8] Das S,Dewanji A,Chakraborty A.Software reliability modeling with periodic debugging schedule[J].IEEE Transactions on Reliability,2016,65(3):1449- 1456.

[9] Chatzis P S,Andreou S A.Maximum Entropy discrimination poisson regression for software reliability modeling[J].IEEE Transactions on Neural Networks and Learning Systems,2015,26(11):2689- 2701.

[10] Lakshmanan I,Ramasamy S.An artificial neural-network approach to software reliability growth modeling[J].Procedia Computer Science,2015,57:695- 702.