改进RSA算法的安全性分析
2018-07-05李云飞刘菊琨云南财经大学研究生部云南昆明650云南中医学院国际交流中心云南昆明650500云南大学软件学院云南昆明65009
李云飞 刘菊琨 柳 青(云南财经大学研究生部 云南 昆明 650)(云南中医学院国际交流中心 云南 昆明 650500)(云南大学软件学院 云南 昆明 65009)
0 引 言
由于RSA密码算法[1]解密过程的大数模幂操作计算会使用大量计算资源,RSA密码算法的性能受到了一定程度的影响。所以多种加快RSA算法解密速度的算法被提出。其中有通过减小模数及模幂指数位数提升运算性能的多素数RSA[2]算法。也有通过在加密过程中完成解密运算转移的负载来加快RSA算法解密速度的算法:RSA-S1系统[3]和RSA-S2[3]等。文献[4-5]中的EAMRSA算法通过结合Multi-Prime和RSA-S2技术加快了算法的解密速度,但文章仅从密钥搜索域对算法进行安全性分析,并未使用连分数和格规约分析方法。
但以上改进算法均通过减小指数d和大数模的位数来提升算法解密操作的速度。1999 年, Boneh 和Durfee[6]在Coppersmith[7]的基础上把位数较少的密钥d的边界值提高到d 本文使用Multi-Prime和RSA-S1负载转移技术使得RSA密码算法解密过程的速度得到了较快提高。为了确保算法的安全性,本文使用May等求取小根的办法,对算法进行格规约分析。经分析当私钥指数个数为2,大数模N素数个数为3时,该改进算法能抵挡格攻击。通过分析及实验测试,得到改进算法在输入高安全参数值时,RSA算法解密性能提升较大。实验测试数据显示与标准RSA算法(解密过程使用中国剩余定理)对比,该算法解密时平均加速比是5.68。 1) 密钥产生算法:算法输入参数为n、b、k、c,公钥和私钥将在该算法中求出,计算步骤如下: (2) 求出和φ(N)彼此互素的公钥指数e,并运算得到d=e-1modφ(N)。 (3) 求出d=d1·e1+…+di·ei+…+dk·ekmodφ(N),1≤i≤k。变量di和ei(1≤i≤k)都是二进制向量,其中每一个di和ei分别是c位随机生成数和|pi-1|位随机生成数。得到公钥和私钥分别是: 公钥: 2) 加密算法: (1) 明文数据M(M∈ZN)和加密指数e作为输入,通过计算C=MemodN得到密文数据C。 (2) 密文数据C作为输入,求出密文向量Z=(z1,…,zk),zi值(1≤i≤k)通过计算zi=CeimodN得到,将向量发送到解密端。 3) 解密算法:解密端输入向量数据Z。解密求解出明文m,具体过程如下: (1) 通过Cj=zimodpj,求出Cj,1≤j≤b,1≤i≤k,zi包含在密文向量Z中。 (4) 获取明文m通过以下计算:m=m1×…×mk=Ce1·d1+…+ek·dkmodN,1≤i≤k,mi=(zi)di=Cei·dimodN。 根据文献[4],RSA算法的1 024位和1 536位的模长安全强度分别对应于对称密码系统中密钥强度为72位和80位[3-4]。所以,在本文以下的数据实验中,从1 024位到3 072位的安全强度范围内,参数k和c分别取值为2和128,参数b取值上限值为3。以上参数值的选取,确保了k×c数值的穷举空较大,确保了EAMS1RSA算法的小位数私钥的安全性。 连分数是初等数论中的基本内容。α的连分数是形式如下的表达式[13],为方便起见,记作α=[a0,a1,a2,…,aN],其中a0是非负整数,a1,a2,…,aN是正整数: 对任意有理数α=b/a,求α的有限连分数展开的计算复杂度实际上与求a和b的最大公因数的欧几里德算法一致,可以在多项式时间内求解。求α的N阶渐近分数的计算复杂度实际上与广义欧几里德算法一致,因而也是一个多项式时间算法[12]。事实上,求α的渐近分数的过程实质上就是求解分母逐渐增大的能够很好地逼近α的一组分数的过程。 定理1[13]令p、q是整数,α是一个实数。如果|p/q-α|<1/(2q2),那么p/q是α的渐近连分数。 EAMS1RSA算法中公钥e和私钥d满足关系:e·d=1 modφ(N),则必存在某个整数k使得ed-k·φ(N)=1。EAMS1RSA算法的大数模N和素数pi,1≤i≤b,需要满足以下两个假设[14]: (1) 设大数模N的b个素数因子满足关系:pi (2)b个素数因子还需要满足以下关系: 4 以上两个假设确保算法得到的素数因子是平衡素数因子,从而来抵御椭圆曲线方法[2]的快速因式分解方法的攻击。 针对拥有b个素数因子的大数模N,可以推出欧拉函数φ(N)的值为[14]: N-φ(N)<(2b-1)N1-1/b 并且可进一步得到定理2。 证明:大数模N的b个素数因子满足关系pi N-φ(N)<(2b-1)N1-1/b 设ed=1+kφ(N)对某个整数k≥1,可推出kN-ed=k(N-φ(N))-1。 在RSA算法中存在某个未知整数k使得公钥和私钥满足等式ed-1=k(N-(p+q-1))。可以使用Coppersmith技术来求解多项式f(x,y,z)=ex-yN+yz-1的整数根(d,k,p+q-1),从而得到大数模N的因子。与此同时,也可以通过求解多项式fe(y,z)=y(N-z)+1mode的模数根(k,p+q-1)来得到N的因子。所以有许多工具被用来解决寻找多项式模数根和整数小根的问题。 引理1[8,11]LLL算法将格L作为输入,其中令格L通过(u1,u2,…,uw)得到,LLL算法产归约向量集合(b1,b2,…,bw)满足。 引理2[11]设L是向量集(u1,u2,…,uw)所生成的格,(b1,b2,…,bw)是格L的LLL归约基,那么‖b1‖≤‖b2‖≤…≤‖bi≤2w(w-1)/4(w+1-i)det(L)1/w+1-i。 本部分将对EAMS1RSA(k=2和b=3,2个小私钥)进行安全性分析,此时EAMS1RSA算法的私钥d可表示为:d=d1e1+d2e2modφ(N)。攻击的成功是假设1成立的前提下: 假设1假设一个包含n个变元的多项式集合{f1,f2,…,fi}的在整数域上的根为(x1,0,x2,0,…,xn,0),其中i≥n。则以结式方式对以上多项式进行求解,能计算得到相应的整数根。 定理3EAMS1RSA的d1和d2私钥指数,对应公钥指数e、e1、e2,大数模N=pqr。令d1,d2 证明:根据EAMS1RSA密码算法存在关系式: d=d1e1+d2e2modφ(N)和ed=1modφ(N) 由以上两式可以推出: e×e1×d1+e×e2×d2=1modφ(N) (1) 由式(1)可进一步推出: ee1d1+ee2d2=1+k(N+r) (2) 式中:r=φ(N)-N。由式(2)可得: ee1d1+ee2d2-1-k(N+r)=0 (3) 安全分析的目的是得到解为k、r、d1、d2的多项式(已知d1 f(x1,x2,x3,x4)=-x1N-x1x2+ee1x3+ee2x4-1 通过S、M以及m值,通过忽略较小的项,求出: 代入X1、X2、X3、X4的值,可得到以下不等式: EAMS1RSA算法相对于标准RSA的理论解密过程的加速比约为:(b·n)/(4·k·c)。 改进算法和相应测试算法是基于OpenSSL实现。平台为:Windows XP操作系统,Intel Pentium双核1.73 GHz处理器,内存1 GB。为了便于描述EAMRSA算法,本文将参数取值b等于3、k等于2和c等于128位的EAMS1RSA改进算法称为EA1M3SRSA算法。 表1显示了RSA改进算法不同位数范围内相对于标准RSA算法的解密加速比情况。从表1中可以看出EA1M3SRSA算法解密时获得的加速比最高。 表1 改进RSA解密加速比 本文运用多素数以及解密转移负载至加密端的方法提出了解密性能提升且可并行的改进RSA算法。同时本文使用连分数和格归约对改进算法进行分析,得到该算法相对于标准RSA算法,也具有较好的安全性。接下来研究的内容是将该算法应用到云安全中。 [1] Rivest R, Shamir A, Adleman L M. A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the Acm, 1978, 26(2):96- 99. [2] Dan B, Shacham H. Fast variants of RSA[J]. Cryptobytes, 2002, 5:1- 9. [3] Castelluccia C,Mykletun E,Tsudik G.Improving secure server performance by re-balancing SSL/TLS handshakes[C]// ACM Symposium on Information, Computer and Communications Security. ACM, 2006:26- 34. [4] 李云飞,柳青,郝林,等.一种有效的RSA 算法改进方案的研究[J]. 计算机应用,2010,30(9): 2393- 2397. [5] 李云飞.RSA密码算法的研究与实现[D].云南:云南大学信息学院,2011. [6] Boneh D, Durfee G. Cryptanalysis of RSA with private key d less than N 0.292[J]. Information Theory IEEE Transactions on, 1999, 46(4):1339- 1349. [7] Coppersmith D. Small solutions to polynomial equations and low exponent RSA vulnerabilities [J].Journal of Cryptology, 1997, 10(4):233- 260. [8] Zheng M, Honggang H U, Wang Z. Generalized cryptanalysis of RSA with small public exponent[J]. Science China(Information Sciences), 2016, 59(3): 97- 106. [9] Sarkar S, Maitra S. Cryptanalysis of RSA with two decryption exponents[J]. Information Processing Letters, 2010, 110(5):178- 181. [10] 李云飞,柳青,李彤,等.对一种改进RSA算法的密码分析[J]. 应用科学学报,2013,31(6): 655- 660. [11] Howgrave-Graham N. Finding Small Roots of Univariate Modular Equations Revisited[C]// IMA International Conference on Cryptography and Coding. Springer, Berlin, Heidelberg, 1997:131- 142. [12] Wiener M J.Cryptanalysis of short RSA secret exponents[J].Information Theory IEEE Transactions on,1990,36(3):553- 558. [13] 韩立东, 王小云, 许光午, 等. RSA密码系统小CRT解密指数的攻击分析[J].中国科学:信息科学,2011,41(2):173- 180. [14] Hinek M J. Cryptanalysis of RSA and Its Variants[M]. Chapman & Hall, 2009.1 EAMS1RSA算法
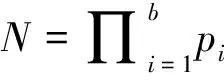

2 EAMS1RSA算法格安全性分析
2.1 EAMS1RSA算法连分数攻击分析
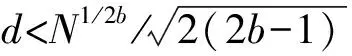

2.2 EAMS1RSA算法格攻击分析





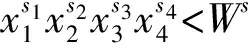

3 理论及验测试结果

4 结 语
