基于模拟退火和历史存档融合的风驱动优化算法

唐 煜 曹小鹏 张 莹(西安邮电大学计算机学院 陕西 西安 710121)

0 引 言

2010年，美国宾夕法尼亚州立大学电气工程系的 Bayraktar Z和Werner D H 博士以及气象学系的Komurcu M博士[1]根据对大气运动的简单模拟提出了风驱动优化算法(WDO)[2-3]。该算法是将空气微团的物理运动模型抽象成简化的空气质点受力运动模型，主要分析空气质点在大气中的受力运动情况，主要考虑四个力：重力、摩擦力、科氏力和大气压力。通过运用牛顿第二定律及理想气体状态方程，推导出空气质点速度方程及位置方程。

相比于其他全局优化算法(如粒子群算法)，风驱动优化算法具有全局搜索能力强、收敛速度较快、精度高、寻优效率高、鲁棒性强，且可以通过微调系数优化算法效果，并且可用于解决多维和多模态问题，可以处理连续和离散优化问题，具有广泛的应用前景。已经被应用于锅炉NO_x排放模型优化[4]、PID参数优化[5]、电磁综合问题[6]、雷达波束图[7]、桥梁有限元模型[8]、非等间距直线阵方向图实例[9]、霍夫变换[10]等场景中。

为了解决风驱动优化算法陷入局部最优时而导致的精度低以及收敛速度慢等问题，本文提出了基于模拟退火和历史存档两者融合的风驱动优化算法，简称WDO-HSSA。实验表明，改进后的算法具有稳定性好、收敛速度快、寻优精度高的特点。

1 风驱动优化算法

1.1 WDO算法的基本原理

风驱动优化算法通过各地气压不同而导致大气运动这一自然现象，建立物理模型，从而得到一种新的全局优化算法。在WDO算法中，研究对象是空气质点，对简化的空气质点运用牛顿第二定律、理想气体状态方程可得空气质点的位置和速度公式[11]。

速度更新公式为：

unext=(1-a)ucur-gxcur+

(1)

位置更新公式为：

xnext=xcur+unext

(2)

式中：ucur为空气质点的当前速度，unext为空气质点下一次迭代的速度，xcur为当前空气质点位置，xbest为最优位置，xnext为空气质点下一次迭代位置，i表示所有空气质点依据适应度值的一个升序排列，uc表示第i个空气质点除k维以外的其他维度的速度，g表示重力相关因数，a表示摩擦因数，R为理想气体常数,T为温度。

风驱动算法步骤如下：

Step1初始化种群规模、维度、最大迭代次数、搜索边界、公式参数、压力函数(即目标函数)。

Step2初始化空气质点，分配初始速度和位置。

Step3计算空气质点压力值并按照压力值大小进行排序。

Step4根据式(1)、式(2)分别更新空气质点的速度和位置。

Step5若未达到终止条件，则转至Step3，若终止，输出最优解。

通常终止条件为足设定一个理想的压力值或初始化的最大迭代次数。

1.2 模拟退火算法

模拟退火算法[12]最早由N.Metropolis等提出，模拟退火思想模拟了热力学中的高温金属冷却的过程，是一种随机组合优化方法。模拟退火算法作为一种通用的优化算法，广泛应用于金融、管理、工程的领域。模拟退火算法模拟热力学中粒子系统降温过程，用于求解最优化问题。当孤立粒子系统温度逐步下降时，以一定概率接受或拒绝新的状态，使粒子系统逐步趋于有序，使系统近似于热力平衡状态，最终系统将达到基态，等同于全局极小点[13]。通过以概率作为接受新状态的方法，可以有效避免搜索陷入局部最优的问题，提高寻优能力。

1.3 历史存档思想

本文提出了一种历史存档的优化思想，它是指通过记录历史数据，完善“自我认知”的过程，它是对历史经验的累积。在处理当代数据时，结合历史经验，能更好地对未来进行决策。

为了减少历史数据的存储，提高算法执行效率，本文提出的历史存档思想采用设置两个历史暂存点，存储与当代最近的间隔相邻周期的全局最优值。利用两个暂存点的大小比较来判断收敛状态以及确定是否需要对种群进行调整。

基于历史存档思想的实施步骤如下：

Step1初始化记录间隔周期T，设置第一次记录时的当前周期为begin，设置记录间隔周期的全局最优解的变量Gbegin、Gbegin+T。

Step2计算该点适应度函数E=f(x)。

Step3是否触发记录条件，如果当前周期为begin+nT(n为1,2,…)，则触发记录条件，继续执行历史存档的判断准则，反之则转至Step5。

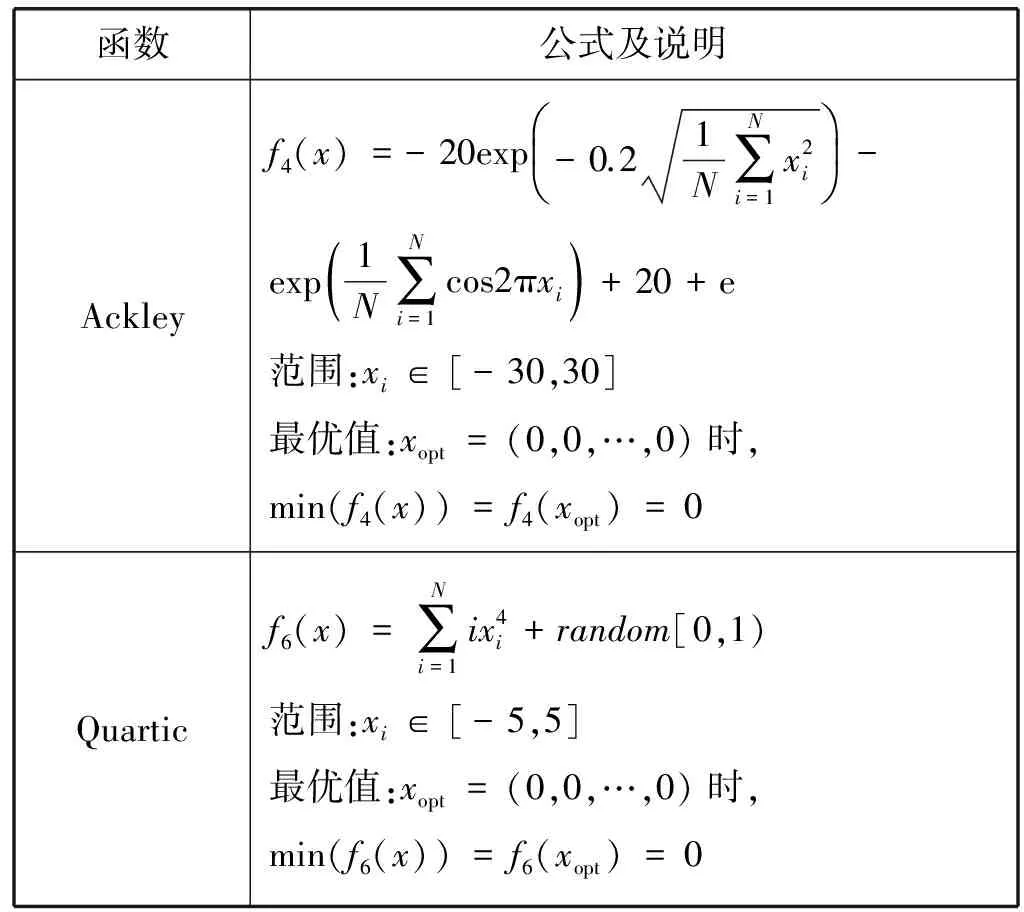
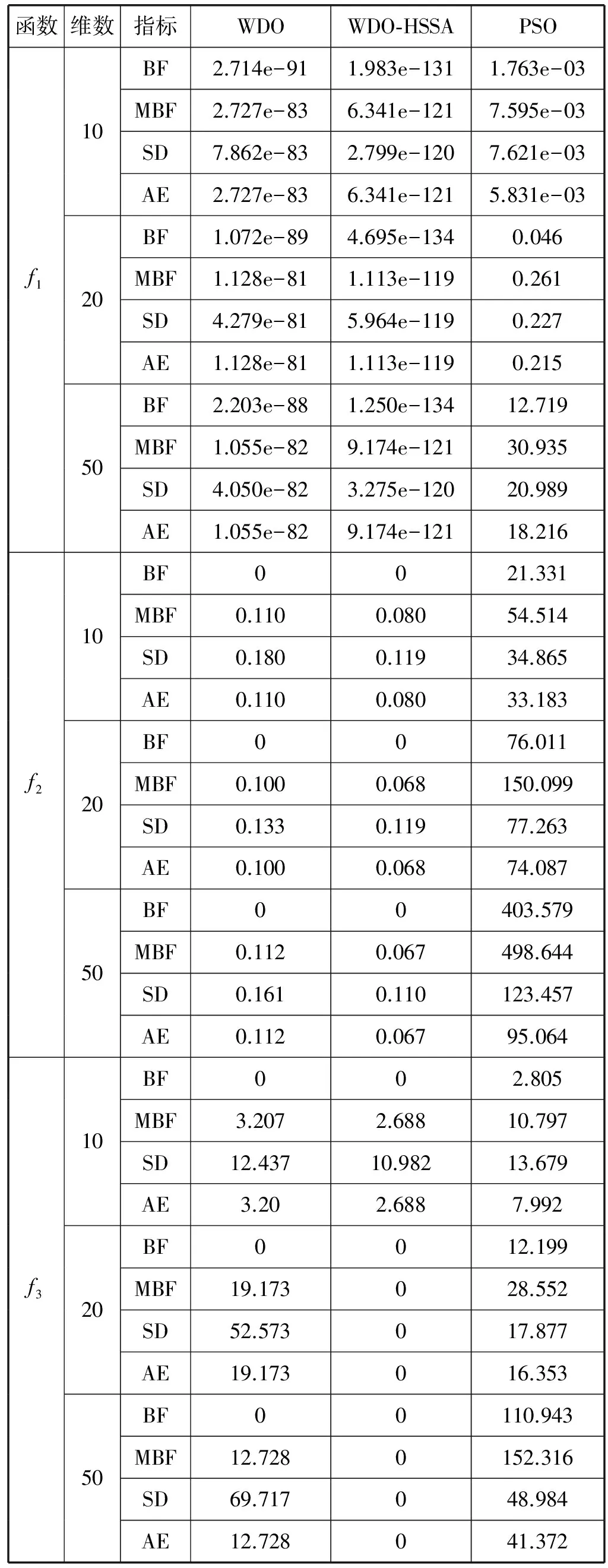
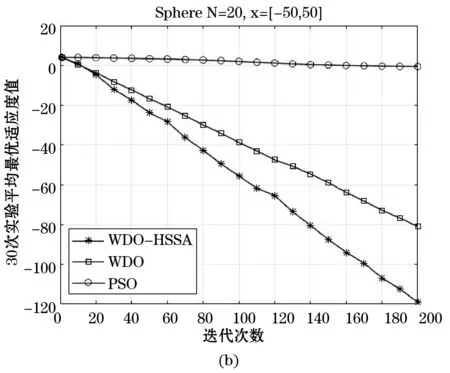
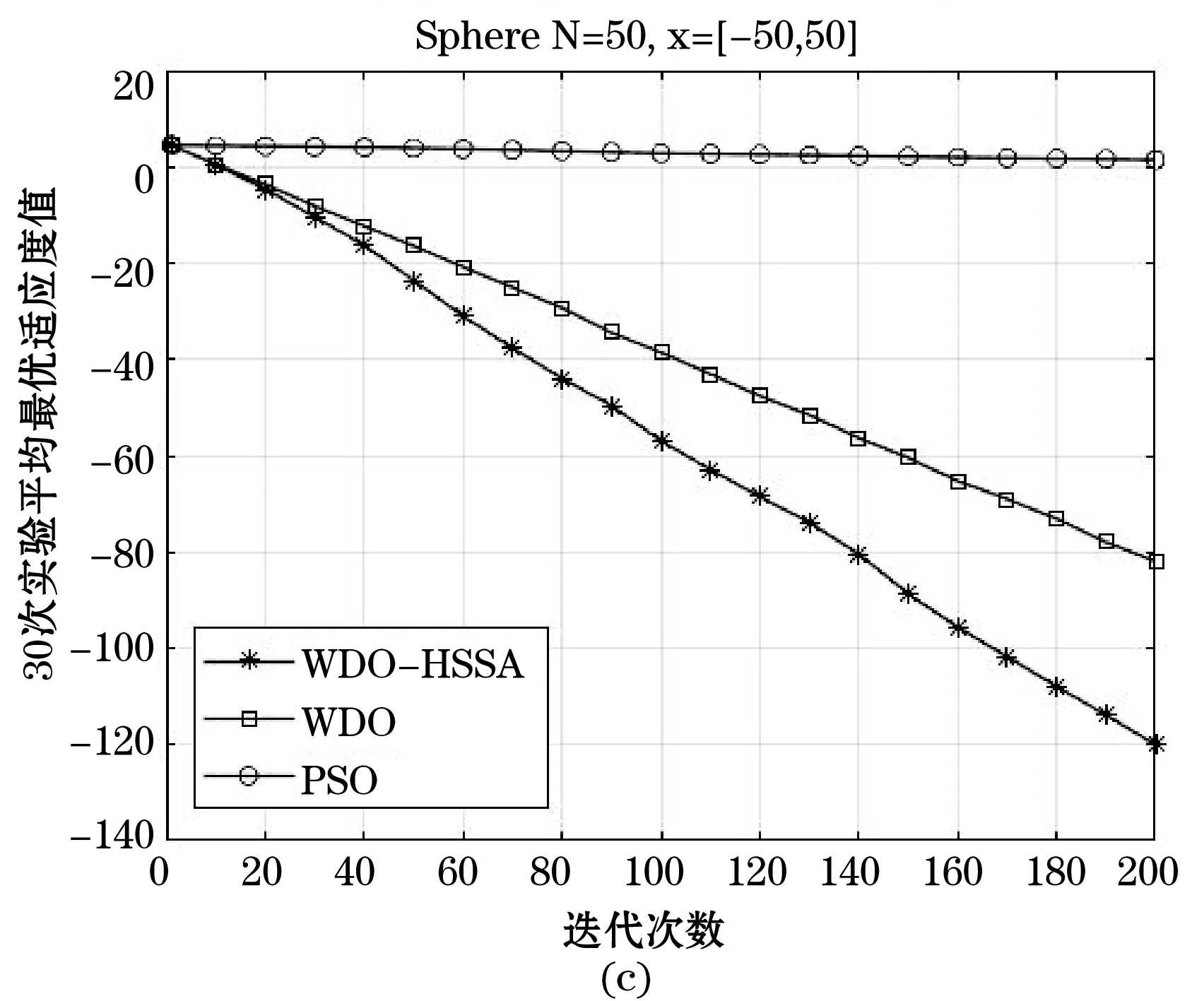
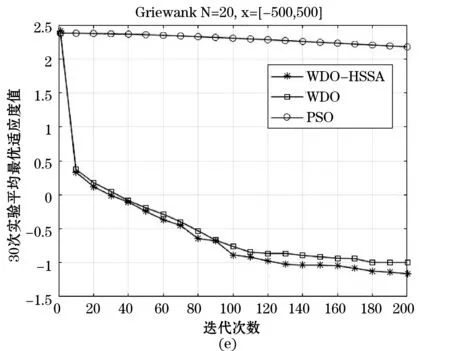
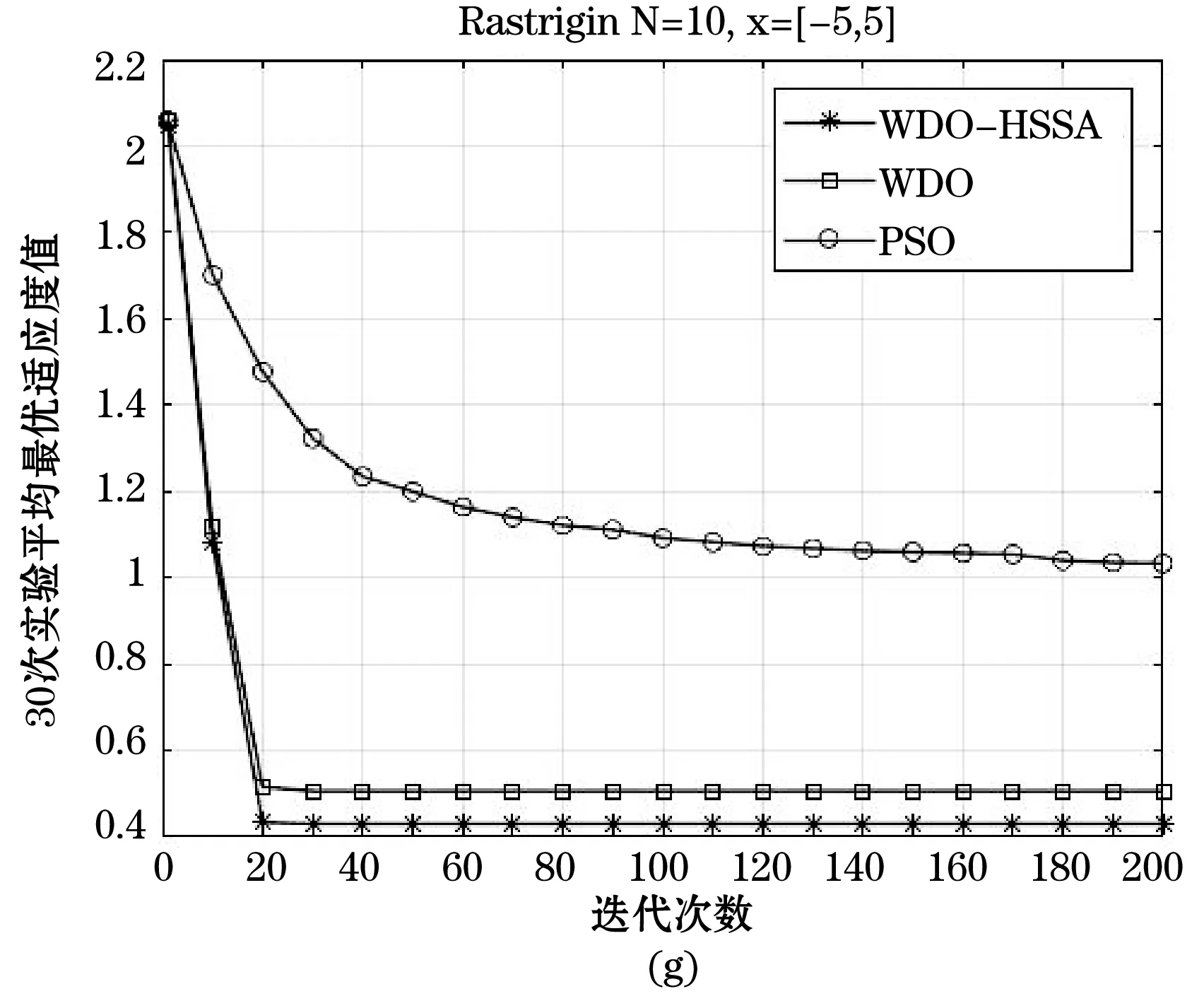
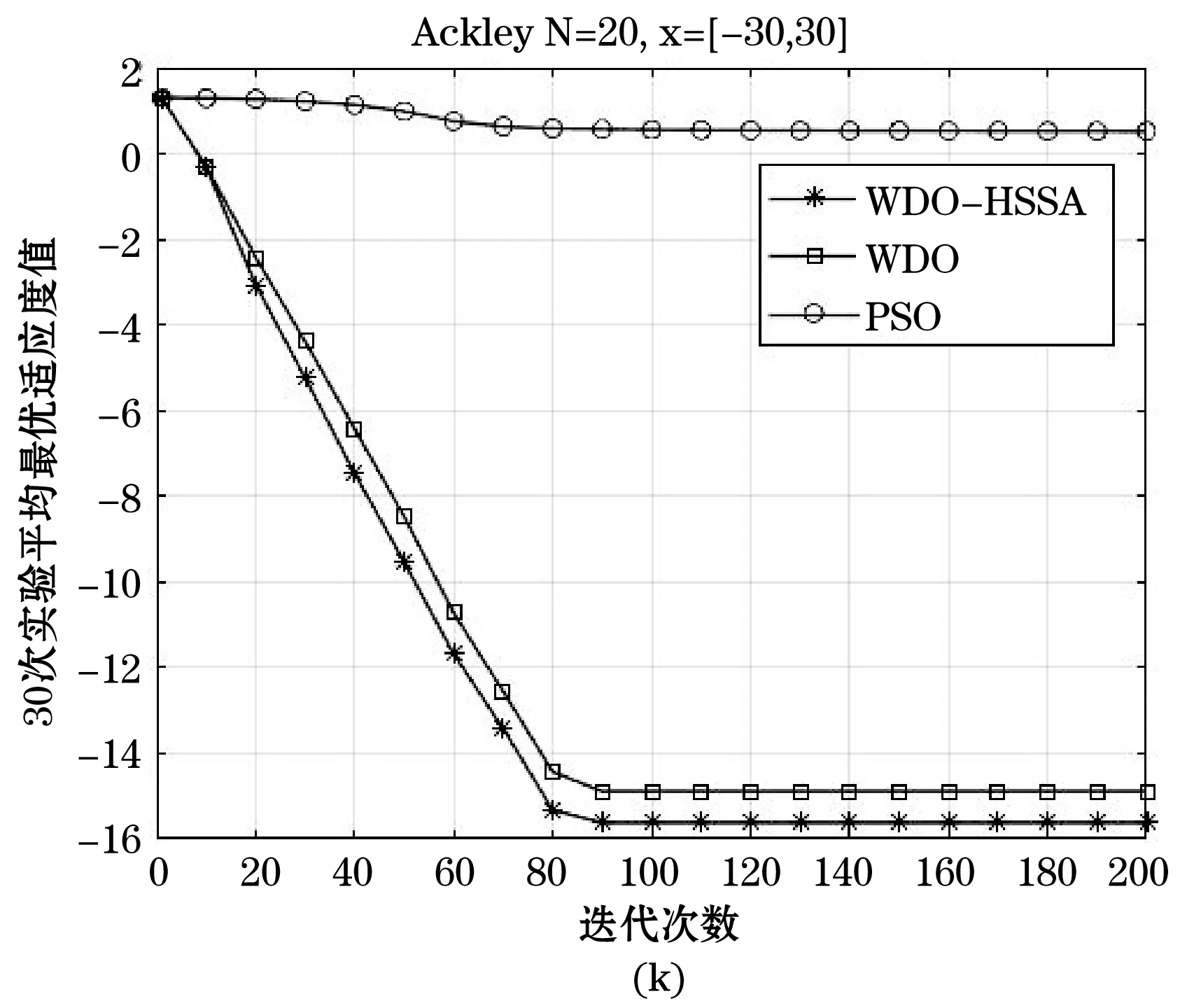
Step4更新Gbegin、Gbegin+T。如若Gbegin

Step5增加迭代次数，当K达到最大迭代次数时停止迭代，否则返回Step2。

以上过程称之为基于暂存点的历史存档准则。

1.4 基于模拟退火和历史存档融合的风驱动优化算法改进

通常WDO算法经过若干次迭代以后，会陷入局部最优解，种群失去了多样性，致使收敛速度变慢，造成早熟。为了解决该问题，本文将模拟退火和历史存档思想融入到风驱动优化算法之中，由此提出了基于模拟退火和历史存档两者融合的风驱动优化算法，简称WDO-HSSA。其中，引入模拟退火思想能使WDO算法避免陷入局部最优的陷阱，同时提高全局搜索能力，引入历史存档思想使算法有效增强陷入局部最优解时的脱困能力。

改进后的WDO算法具体步骤如下：

Step1初始化种群规模、维度、最大迭代次数、搜索边界、公式参数、压力函数(即目标函数)。

Step2初始化空气质点，分配初始速度和位置。

Step3计算空气质点压力值并按照压力值大小进行排序。

Step4更新空气质点的速度和位置。

Step5计算当前解与新解的适应度值，利用Metropolis准则更新全局最优值。

Step6判断适应度值否达到要求，若满足则执行降温操作，反之，则转至Step8。

Step7降温退火操作。

Step8每隔预先设置的代数则对相应周期的历史全局最优解记录存档。

Step9根据历史存档的准则决定是否变异部分空气质点速度和位置。

Step10若未达到终止条件，则转至Step3，若终止，输出最优解。

通常终止条件为一个理想的压力值或初始化的最大迭代次数。

2 实验设计及仿真分析

2.1 测试函数设计

为了评价优化算法性能，本文采用了表1所示的五种标准测试函数对风驱动优化算法(WDO)、基于模拟退火和历史存档融合的风驱动优化算法(WDO-HSSA)、粒子群算法(PSO)[14-16]进行测试。分别是Sphere函数、Griewank函数、Rastrigrin函数、Ackley函数、Quartic函数。表1所示为五种测试函数的公式定义以及实验用到的搜索范围和函数的最优值。

表1 测试函数基本信息

续表1

2.2 实验条件设计

每个算法实验按照维度的不同划分为三组，分别是维度N=10、N=20、N=50三组，随着维度的增加，测试难度不断增大，更加能反映算法在不同维度下的搜索能力，体现出算法综合性能。每组实验在每个测试函数下都独立执行30次，记录下30次执行后的最优适应度值BP(Best Fitness)、平均最优适应度值MBF(Mean Best Fitness)、标准差SD(Standard Deviation)、平均适应度值误差AE(Average Error)这四组数据，其中BF反映了算法寻优的极限能力，BF越接近极值，则算法极限搜索能力越强。MBF反映了算法寻优的平均能力，MBF越小，则算法平均搜索能力越强。SD反映了算法在多次重复寻优过程中的稳定性，SD越小，则算法稳定性越强。AE反映了算法性能优越性，当AE越小，算法性能通常越优，AE的计算公式为AE=MBF-BF。

在实验设计中，三个算法的参数始终保持一致。具体设置如下：种群数为40，搜索范围见表1，最大搜索速度都为1。其中，WDO参数设置如下:a=0.7、g=0.8、RT=0.7、c=0.42。WDO-HSSA参数设置如下:a=0.7、g=0.8、RT=0.7、c=0.42、T=初始化全局最优值、r=0.9、Tmin=0。PSO参数设置如下:c1=2、c2=2、w=0。实验仿真环境为MATLAB R2017a。

2.3 结果分析

根据表2中最优适应度值(BF)可以看出，WDO-HSSA算法、WDO算法在标准测试函数f1、f2、f3、f4、f5下寻优精度对比PSO算法均有一定的提升，其中对于函数f1、f4均有10个数量级以上的提升。随着维度的增加，WDO-HSSA算法在BF这一指标上优势越来越明显。可以得出结论，在BF指标上WDO-HSSA算法最好，其次是WDO算法，PSO算法最差，这说明WDO-HSSA的极限寻优精度的能力上比起WDO算法以及PSO算法更强。

表2 多组测试函数不同维度下的仿真结果

续表2

图1所示为三种算法的平均最优适应值曲线，其中，横轴表示迭代次数，纵轴表示30次实验平均最优适应度值的对数，每幅子图顶部标明了对应的标准测试函数及其测试维度和搜索范围。根据表2中平均最优适应度值(MBF)及图1可以看出，WDO-HSSA、WDO算法在测试函数f1、f2、f3、f4、f5下MBF指标比PSO算法MBF指标更优。可以得出结论，在MBF指标上WDO-HSSA算法最好，其次是WDO算法，PSO算法最差，这说明WDO-HSSA的平均寻优精度的能力上强于WDO算法以及PSO算法。

根据表2中标准差值(SD)可以看出，WDO-HSSA算法、WDO算法在标准测试函数f1、f2、f3、f4、f5下标准差值对比PSO算法均有较为满意的解。可以得出结论，在SD指标上WDO-HSSA优于WDO算法，PSO算法最差，这说明WDO-HSSA算法在算法稳定性上最好，其次是WDO算法，最差为PSO算法。

根据表2中平均适应度值误差(AE)可以看出，WDO-HSSA算法、WDO算法在标准测试函数f1、f2、f3、f4、f5下标准差值对比PSO算法均有较为满意的解。随着维度的增加，这一指标的优势越来越明显。可以得出结论，在AE指标上WDO-HSSA算法最好，其次是WDO算法，PSO算法最差，说明WDO-HSSA算法性能优越性上好于WDO算法，最差是PSO算法。

综上所述，在BF、MBF、SD、AE四组指标下，可对三种算法的寻优性能排序如下：WDO-HSSA>WDO>PSO。随着维度的提升，WDO-HSSA算法的在四组指标下的优势也是越来越明显。所以无论从算法精度层面考虑还是从稳定性层面考虑，WDO-HSSA算法具有更强的寻优能力。

3 结 语

风驱动的优化算法是一种基于自然启发式的全局优化算法。本文在标准的风驱动优化算法下引入了模拟退火思想以及历史存档思想来完成对算法的进一步改进。通过模拟退火机制能更好地避免陷入局部最优问题，模拟退火接受变异的种群，随着迭代、温度的下降，接受概率逐渐减小，从而提高了收敛性能。通过引入历史存档机制，在发现陷入局部最有问题时，变异一定数量种群，使算法能有效提高陷入局部最优问题时的摆脱能力。所以基于模拟退火以及历史存档融合后的算法能有效提高避免陷入局部最优的能力以及陷入局部最优时的脱困能力,增强全局搜索能力以及寻优精度。通过测试仿真结果表明，HSSA-WDO算法的性能优于WDO算法以及PSO算法。

[1] Bayraktar Z, Komurcu M, Werner D H. Wind Driven Optimization (WDO): A novel nature-inspired optimization algorithm and its application to electromagnetics[C]// Antennas and Propagation Society International Symposium. IEEE, 2010:1- 4.

[2] Bayraktar Z, Komurcu M, Bossard J A, et al. The Wind Driven Optimiazation Technique and its Application in Electromagnetics[J]. IEEE Transactions on Antennas & Propagation, 2013, 61(5):2745- 2757.

[3] Bayraktar Z, Komurcu M, Jiang Z H, et al. Stub-loaded inverted-F antenna synthesis via Wind Driven Optimization[C]// IEEE International Symposium on Antennas and Propagation. IEEE, 2011:2920- 2923.

[4] 牛培峰, 赵振, 马云鹏,等. 基于风驱动算法的锅炉NOx排放模型优化[J]. 动力工程学报, 2016, 36(9):732- 738.

[5] 陈彬彬, 曹中清, 余胜威. 基于风驱动优化算法WDO的PID参数优化[J]. 计算机工程与应用, 2016, 52(14):250- 253.

[6] 任作琳. 风驱动优化算法及其在电磁综合问题中的应用研究[D]. 江苏科技大学, 2016.

[7] 毛晟,张贞凯,田雨波. 基于风驱动算法的机会阵雷达波束图综合[J]. 江苏科技大学学报(自然科学版),2017,31(4):485- 489.

[8] 周赤伟. 基于泰勒展开式和风驱动优化算法的桥梁有限元模型修正研究[D]. 北京交通大学, 2016.

[9] 任作琳,田雨波,孙菲艳. 基于改进风驱动算法的非等间距直线阵综合[J]. 计算机科学,2016,43(7):268- 274.

[10] 范旭,曹中清,陈彬彬. 基于风驱动优化的霍夫变换算法[J]. 计算机工程与设计,2017,38(6):1522- 1525.

[11] 任作琳,田雨波,孙菲艳. 具有强开发能力的风驱动优化算法[J]. 计算机科学,2016,43(1):275- 281,305.

[12] 庞峰. 模拟退火算法的原理及算法在优化问题上的应用[D].吉林大学,2006.

[13] 卢宇婷,林禹攸,彭乔姿,等. 模拟退火算法改进综述及参数探究[J]. 大学数学,2015,31(6):96- 103.

[14] 随聪慧. 粒子群算法的改进方法研究[D].西南交通大学,2010.

[15] 李志,陈年生,郭小珊,等. 粒子群算法及其改进技术研究[J]. 湖北师范学院学报(自然科学版),2011,31(2):104- 108.

[16] 白艳敏. 粒子群算法及其应用研究[D].兰州交通大学,2013.