受到恶意程序攻击的MWSNs节点状态时空动力学分析

赵金皓 曹奇英* 沈士根(东华大学计算机科学与技术学院 上海 060)(绍兴文理学院计算机科学与工程系 浙江 绍兴 3000)

0 引 言

移动传感网MWSNs(Mobile Wireless Sensor Networks)由有移动特性的传感节点组成，具有灵活度高、覆盖度广、通信能力强等特点，在工业界及学术研究领域等方面有着广泛的应用[1-3]，比如医疗检验、环境监督等。

由于MWSNs中的传感节点存有大量的有价值的数据及信息，其安全性十分重要。恶意程序通过感染健康的传感节点，能获取节点中保存的数据信息及阻断节点间的正常通信，从而对MWSNs的安全造成威胁。另外，近期的研究成果[4]表明，由于组成同一个MWSNs的传感节点的软件与硬件的结构相同，如果一个传感节点被恶意程序感染，很容易传染给在其通信范围内的其他节点，再加上MWSNs中节点的移动特性，恶意程序很容易感染到整个MWSNs中。因此，MWSNs的安全问题受到很大挑战，对恶意程序传播机制的研究十分必要。

由于恶意程序在MWSNs中对传感节点的感染与流行病的传播方式有着相同的特性[5]，因此，常常根据流行病模型的理论来模拟恶意程序的传染过程，即通过流行病模型建立恶意程序在MWSNs中的传染模型。首先，定义传感节点的几种不同状态，如易感(Susceptible)节点、感染(Infected)节点、免疫(Recovered)节点等。再根据不同的传感节点状态，得到恶意程序的传染模型，如SI(Susceptible-Infected)模型、SIS(Susceptible-Infected-Susceptible)模型、SIR[6](Susceptible-Infected-Recovered)模型及SIRD[7](Susceptible-Infected- Recovered-Dead)模型。文献[8]描述了社交网络中的信息扩散行为。除了传染病模型，马尔科夫链[9]及元胞自动机[10-11]等方法也用于模拟WSNs中恶意程序的传播过程。文献[12]基于元胞自动机，分析了恶意程序在广播协议中的传播行为。文献[13]建立了基于有向天线WSN中的病毒传播模型。文献[14]将博弈论与传感网相结合，建立了WSN的节点信任模型，描述了节点信任演化动力学规律。文献[15]使用最优反应均衡预测传感网恶意程序的行为以解决重复博弈纳什均衡解求解困难的问题，给出抑制传感网恶意程序传播的算法。文献[16]基于博弈论分析恶意软件的支付，以预测其在WSN中的传染行为。

本文将MWSNs抽象为一个二维空间，基于流行病理论建立恶意程序的节点状态转换模型；根据一定区域内节点数量随着时间不断变化的情况，建立传感节点状态变化的时空动力学微分方程组，即节点时空动力学模型，计算分析得到模型的平衡点，并通过Matlab仿真影响模型收敛的因素，对比不同的扩散速度、传播半径及发包率对系统收敛的影响。

1 网络模型

由于MWSNs中的节点是持续不断移动的，因此，随着节点的移动，MWSNs的拓扑结构不断变化，数据的通信链路也随之变化。为了研究传感节点的状态与运动情况，假定MWSNs部署在一个方形的二维空间中，该空间由n×n个方形网格组成，每个小方格用二维坐标表示其空间位置，如图1所示。

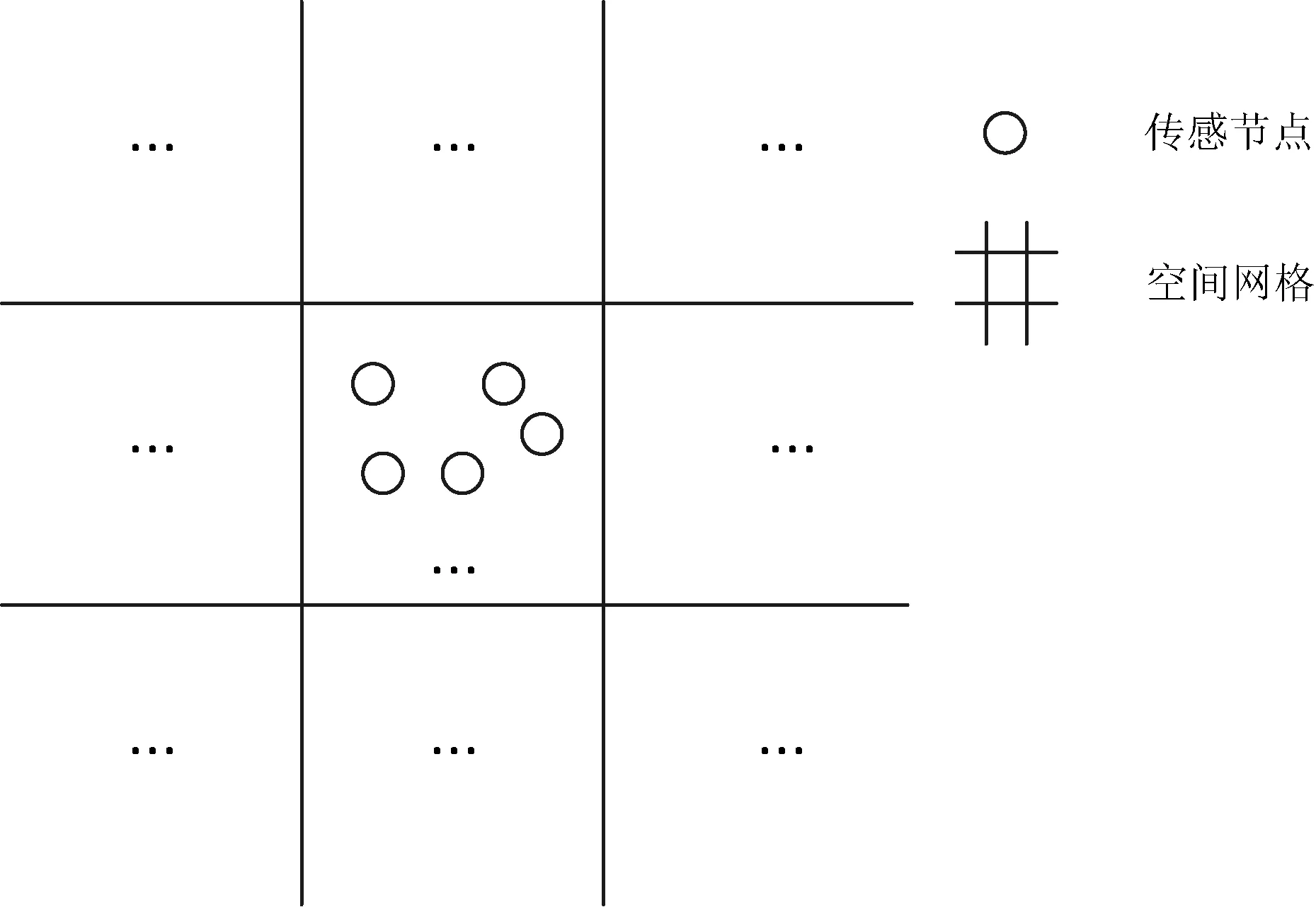
图1 MWSNs的网络模型

空间网格中存在着大量具有移动特性的传感节点，为了分析恶意程序在MWSNs中的传播情况，就要对节点在网络中的时间及空间的分布情形、节点所处的状态进行描述。设节点所在的网格用空间坐标(x,y)来表示，其中，0≤x≤n，0≤y≤n。设在任意时刻t，整个MWSNs中的传感节点以相同的速度t沿着任意方向进行随机的移动，在节点移动过程中，其所在的网格不断变化，那么表示节点空间位置的二维坐标也在不断变化。因此，一个空间网格(x,y)内的节点数量及密度都将随着节点的移动不断地变化，也即随着时间的推移增加或减少。设σ表示整个方形二维空间的面积，又因为整个空间有n×n个方形网格，那么，每个网格的面积σ1为：

σ1=σ/(n×n)

(1)

设m表示整个网络空间内节点的数量，那么，单位面积内的节点数量m1为：

m1=m/σ

(2)

设θ(x,y)表示空间网格(x,y)的面积，根据上述的网格面积及单位面积内节点数量的描述可得，在任意时刻t，空间网格(x,y)内活动节点的数量m(x,y,t)为：

m(x,y,t)=m1θ(x,y)=mθ(x,y)/σ

(3)

又因为假定网络空间内的每个方格的面积相等，那么空间网格(x,y)内的活动节点数可以表示为：

m(x,y,t)=m1σ1=m/(n×n)

(4)

除了节点的移动速度及方向、网格的面积、网格内活动节点数量等参数，还需几个重要参数来描述MWSNs的模型，有通信半径、发包率、发包成功率等。

在MWSNs内，如果两个节点能够直接相互交换数据及信息、直接进行通信，那么称这两个节点为邻居节点；节点与其邻居节点之间的距离为通信半径，不同网络中的节点通信半径也不同。用r表示MWSNs中移动节点的通信半径，可以得到传感网中每个节点的邻居节点的数量为：

ml=πr2m1=πr2m/σ

(5)

假设每个传感节点的发包率、发包成功率都相同，用p表示节点的发包率，ρ表示节点的发包成功率。其中，0≤p≤1,0≤ρ≤1。

2 MWSNs恶意程序的传播机制

在MWSNs中，恶意程序通过攻击健康的传感节点进行传播，并获取节点中存储的数据。接下来根据经典的流行病理论描述恶意程序的传播过程，从而建立传播模型。

随着时间的推移，MWSNs中节点的状态不断地变化。本文将传感节点划分为以下五种状态，分别是易感(Susceptible)节点、感染(Infected)节点、免疫(Recovered)节点、潜伏(Exposed)节点、死亡(Dead)节点，为了方便表述，分别用S,I,R,E,D表示。其中，易感节点是指尚未被恶意程序传染，但在将来可能被感染的节点；感染节点是指已经被恶意程序传染并具有传染能力的节点；免疫节点是指曾被恶意程序感染，但是恶意程序已经被清除，且不会再被恶意程序感染的节点；潜伏节点是指已经被恶意程序感染，暂时不具备感染其他节点的能力，但在将来可能具备传染能力的节点；死亡节点是指由于受到了攻击或者能量不足等原因而不具备存储和发送数据能力的节点，且其不具备移动能力。其中，潜伏节点会在潜伏时间结束后转换为感染节点，具备传染能力，设在任意时刻t，潜伏节点以平均概率k1转换为感染节点。被恶意程序攻击成功的易感节点，有概率j1转换为感染节点，概率j2转换为潜伏节点。

在MWSNs中，随着节点的移动与时间的推移，传感节点的状态不断改变，构成状态空间，节点状态变化的情况可用状态转换模型来表示，如图2所示。

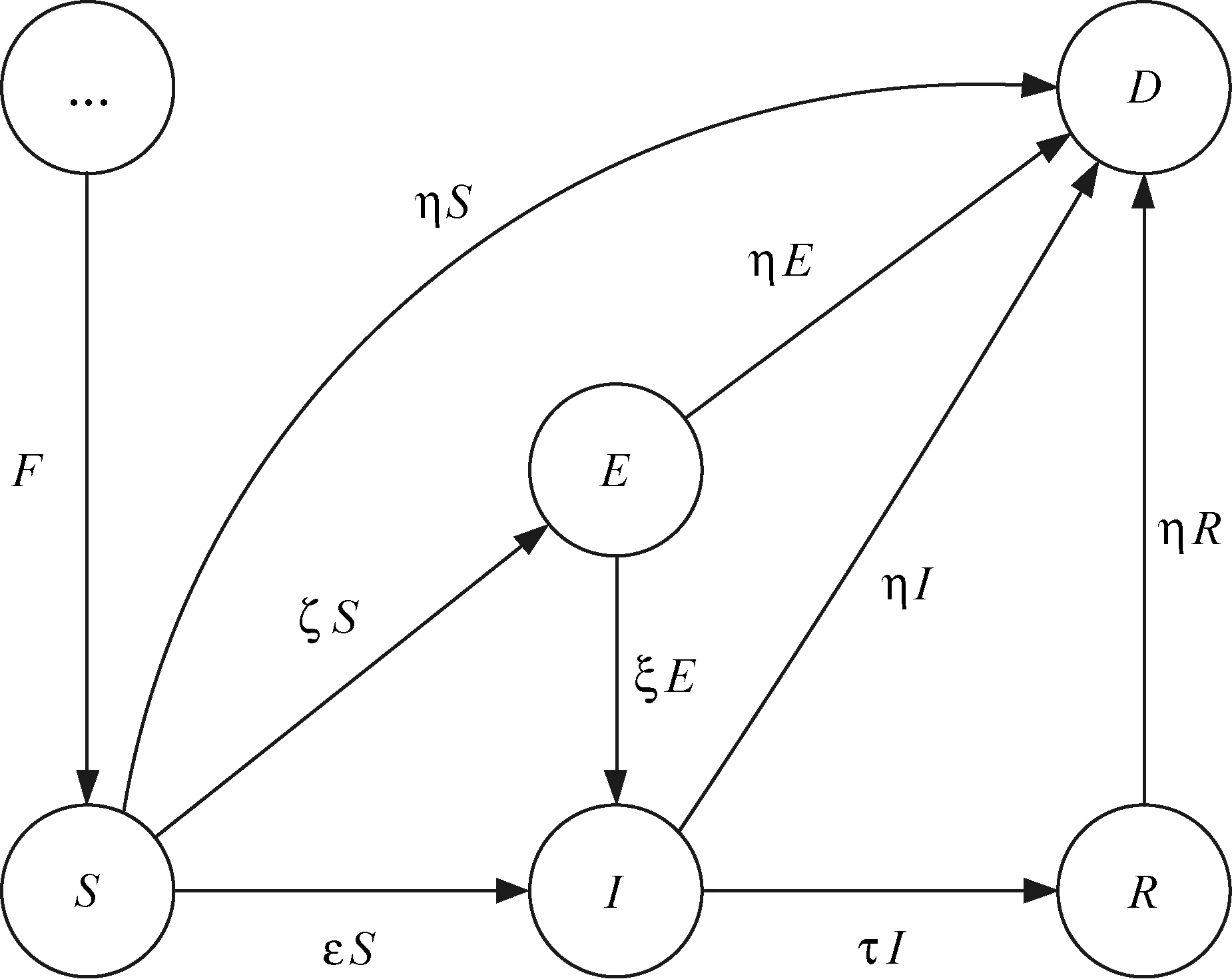
图2 传感节点的状态转换关系图

图2中，F表示单位时间内向网络中加入新健康节点的概率，从而维持MWSNs中节点的总体数量，η(0≤η≤1)表示节点的死亡概率；ε(0≤ε≤1)表示易感节点转换为感染节点的概率；ζ(0≤ζ≤1)表示易感节点转换为潜伏节点的概率；ξ(0≤ξ≤1)表示潜伏节点转换为感染节点的概率；τ(0≤τ≤1)表示感染节点转换为免疫节点的概率。

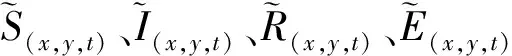
(6)

(7)

简化可得：

(8)

那么，由一个节点的邻居节点数量及易感节点在区域(x,y)内的数量占比，得到在MWSNs中的空间网格(x,y)内，一个感染节点的邻居节点中易感节点的数量为：

(9)

简化可得：

(10)

再根据移动节点的发包率p、发包成功率ρ，以及能够和一个感染节点直接通信的易感节点的数量，那么，可以得到一个感染节点能够成功传染的易感节点的数量为：

(11)

另外，随着恶意程序的扩散，网络系统中易感节点的数量不断下降，恶意程序对易感节点的传染会出现饱和现象，本文引入参数α表示饱和度，β表示传感网的调节指标。当β越小时，α增长速度越快，也就越容易达到峰值；当β越大时，α增长速度越慢，达到峰值也越迟。在时刻t，空间网格中(x,y)中易感节点传染饱和度数学表示如下：

(12)

3 MWSNs节点状态时空动力学系统

3.1 MWSNs恶意程序的扩散方程

MWSNs所在的二维空间内，大量的活动节点以相同的概率选择其移动的方向并以速度v沿着已选择的方向移动。随着时间的推移，这种移动导致空间网格(x,y)中的S、I、R、E四类节点的分布比例发生着变化。为了表达简洁，用参数μ来代替式(11)的一部分。

μ=πr2(1-(1-ρ)P)/σ(x,y)

(13)

随着二维空间中节点的移动，一个传感节点的邻居节点数量及不同状态节点的占比也在不断地变化。因此，当易感节点进入到感染节点的传播范围内，感染节点有一定概率成功攻击易感节点。四类节点S，I，R，E的反应扩散情况可以用下面的方程组来表示，即节点的扩散方程。方程组如下：

(14)

▽2=∂2/∂x2+∂2/∂y2

(15)

3.2 基于恶意程序传播行为的MWSNs节点状态时空动力学系统

根据图2的节点状态转换关系图，代入具体参数，可得恶意程序扩散方程如下：

(16)

因此，根据恶意程序在MWSNs的传播行为及节点状态转换关系可得到相应的时空动力学系统如下：

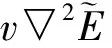
式(21)对S、I、E、R四种节点在MWSNs的初始状态作了描述，表示在初始状态下四种节点共存。其中，S0、I0、E0、R0分别表示易感节点、感染节点、潜伏节点及免疫节点的初始密度。式(22)表示MWSNs系统是封闭的，是一个自治的系统，即MWSNs中的节点不受外部的影响，且没有传感节点移出MWSNs网络空间。

3.3 系统平衡点的分析

当系统随着时间的推移最终达到收敛的状态，即四种节点的数量不再随着时间变化时，说明系统达到了平衡状态。系统的平衡点分为地方病平衡点和无病平衡点，地方病平衡点是指系统收敛到四种节点共存时的解，此时，恶意程序持续传播并且保持着一定的传播水平；无病平衡点是指在系统收敛到感染节点数量为0的状态，此时，恶意程序在MWSNs中已经消亡。

由非线性系统的理论，系统的扩散行为并不影响其平衡点的存在性，即扩散系统与其相对应的非扩散系统具有一致的平衡点。因此，可以抽取系统的非扩散部分来解决问题，并且，免疫节点的密度变化可以根据其他三种节点进行求解。其中，非扩散系统如下：

至此，求解MWSNs节点状态时空动力学的问题就转化成了求解式(23)-式(25)常微分方程组的问题。根据常微分方程组的求解方法，当满足如下条件时，能够求解其平衡点：

(26)

根据式(19)条件求解式(18)，并将描述饱和度的参数代入，可得下列等式：

(27)

(28)

(29)

由式(29)得到：

(30)

再将式(30)代入式(28)，可得：

(31)

求解得：

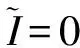
(32)

(33)

将式(32)代入式(33)，得到：

(34)

(35)

式中：A=(η+τ)(η+k1)(j1μ-j2μ-ηβ)；B=-Aμ(j1η+j1k1+j2k1)；C=-η(η+τ)(η+k1)。

对式(35)进行求解，分为三种情况。

情况一：若B2-4AC<0,即B2<4AC，这时式(35)没有解。由此表明式(23)-式(25)的系统不存在正平衡解，即该系统恒有一个无病平衡解。因此，系统式(17)-式(22)也恒有一个无病平衡解E0。

情况二：若B2-4AC=0，即B2=4AC，此时式(35)有唯一的根，也即式(23)-式(25)的系统有一个正平衡解，将A,B,C值代入，解得：

(36)

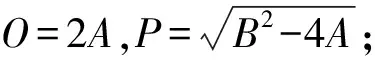
(37)

4 数值仿真及分析

为了直观地展现受恶意程序攻击的MWSNs节点状态的时空特征，使用实验工具Matlab R2014a对时空动力模型进行数值仿真。通过模拟易感节点、感染节点、潜伏节点及免疫节点等不同状态的节点在网络空间内的数量及位移的变化情况，定量地分析恶意程序的传染对MWSNs收敛状态的影响，为防御恶意程序的攻击提供支持。

对以偏微分方程组为形式的系统进行求解时，将时间连续的恶意程序扩散方程在二维空间进行离散化，其中，二维空间即为n×n个方形网格。每个网格的边长是相等的，记为Δh。通过差分方法离散表示节点移动过程的Laplace算子，记离散化的时间为Δt。

根据经验设置数值仿真参数如下：M=100，Δh=2，Δt=0.01，添加新节点率F=0.2，节点死亡率η=0.053，发包成功率ρ=0.6，潜伏节点到感染节点的转换率ξ=0.3，感染节点到免疫节点的转换率τ=0.329 8，易感节点到潜伏节点的转换率ζ=0.064 3，易感节点到感染节点的转换率ε=0.257 2，饱和系数β=2。另外，设感染节点在网络中的初始密度为0.2。值得说明的是，上述参数值会影响系统收敛的时间，但整个数据曲线变化趋势不变。

4.1 扩散速度对恶意程序传播的影响

对于情形一，当系统恒有唯一的无病平衡点时，为了研究不同的节点移动速度对感染节点数量变化的影响，以及分析对系统达到收敛状态速度的影响，设节点移动的速度分别为v=0,20,40，另外，设通信半径r=8，发包率p=0.6。仿真结果如图3所示。

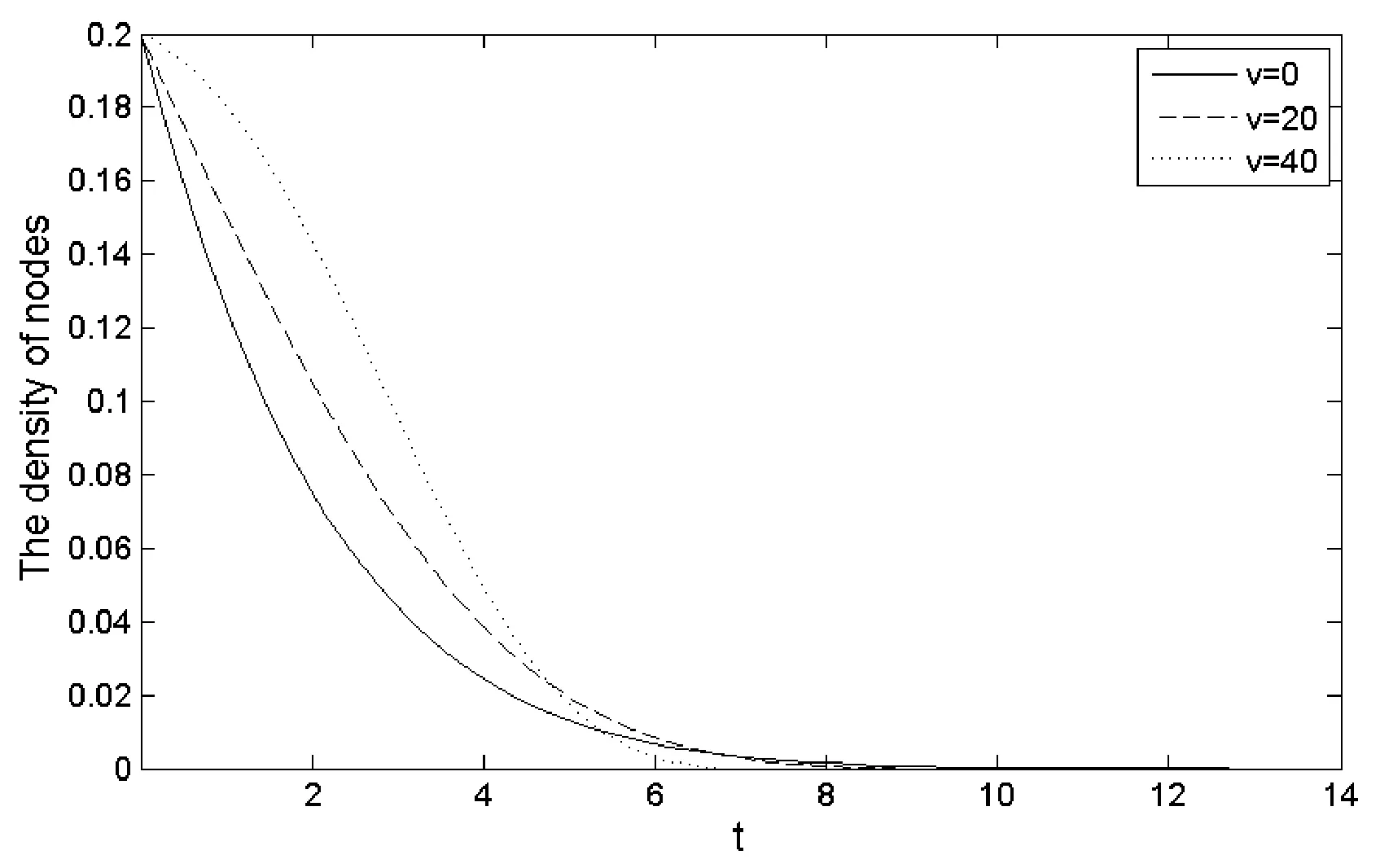
图3 不同扩散速度的感染节点密度变化图

通过图3可以看出，对三种不同的节点扩散速度进行仿真，随着扩散速度v的增长，系统越快达到收敛的状态，即感染节点越快在空间中消亡，系统收敛于无病平衡点E0。其中，当扩散速度v=0时，即节点不移动的情况，此时网络系统相当于传统的静态传感网，是本次研究的特殊情况。通过仿真可以得出，当扩散速度越快，易感节点更容易移动到感染节点的通信范围内，因此促进系统收敛达到平衡状态。

4.2 通信半径对恶意程序传播的影响

对于情形一，当系统恒有唯一的无病平衡点时，为了研究不同大小的节点间不同通信范围对感染节点数量变化的影响，以及分析对系统达到收敛状态快慢程度的影响，设节点的移动半径分别为r=4,8,12，另外，设节点的移动速度v=20，发包率p=0.6。仿真结果如图4所示。

图4 不同传播半径的感染节点密度变化图

通过图4可以看出，对三种不同的节点间的通信范围进行仿真，随着通信半径r的增加，系统越快达到收敛的状态，即感染节点越快在空间中消亡，系统收敛于无病平衡点E0。通过仿真可以得出，当节点的通信半径越大，易感节点更容易与感染节点取得通信，完成信息交换，更易传染恶意程序，因此促进系统收敛达到平衡状态。

4.3 发包率对恶意程序传播的影响

对于情形一，当系统恒有唯一的无病平衡点时，为了研究不同的节点发包率对感染节点数量变化的影响，以及分析其对系统达到收敛状态快慢程度的影响，设节点的发包率所取的数值分别为p=0.4,0.6,0.8，另外，设节点的扩散速度v=20，节点间的通信半径r=8。仿真结果如图5所示。

图5 不同发包率的感染节点密度变化图

通过图5可以看出，对三种不同的节点间的发包率进行数值仿真，随着传感节点发包率p值的增加，系统越快达到收敛的状态，即感染节点越快在网格空间中消亡，系统收敛越快于无病平衡点E0。通过仿真可以得出，当节点的发包率越大，感染节点与易感节点发生信息交换的频率越快，使得恶意程序更容易对易感节点进行攻击，加速了恶意程序的传播，因此促进系统收敛更快达到平衡状态。

5 结 语

本文为了分析恶意程序的传染行为对MWSNs的影响，建立了节点状态的时空动力学系统。通过流行病理论，描述了MWSNs中各类节点的转换制约关系，分析了恶意程序的传播行为。通过扩散方程，建立了节点状态的时空动力学系统，并求解出系统的无病平衡点。实验仿真了不同因素下的的系统收敛时间，分析了不同的节点移动速度、传播半径及发包率对系统收敛到无病平衡状态的影响。

但是，本文对系统的求解没有考虑到正平衡点，在正平衡状态下，恶意程序在MWSNs中持续传染，并维持在一定的传染水平，该状态对MWSNs中节点时空动力系统的分析有重要意义。因此，下一步工作将在考虑正平衡状态下系统的收敛。

[1] Granjal J, Monteiro E, Silva J S. Security in the integration of low-power Wireless Sensor Networks with the Internet: A survey[J]. Ad Hoc Networks. 2015, 24(PA): 264- 287.

[2] 张惠根, 周治平. 一种强安全的WSN用户认证及密钥协商方案[J]. 传感技术学报, 2015, 28(8): 1207- 1214.

[3] Winkler T, Rinner B. Security and Privacy Protection in Visual Sensor Networks: A Survey[J]. ACM Computing Surveys, 2014, 47(1): 1- 42.

[4] Wang Y, Wen S, Xiang Y, et al. Modeling the Propagation of Worms in Networks: A Survey[J]. IEEE Communications Surveys & Tutorials, 2014, 16(2): 942- 960.

[5] 沈士根, 黄龙军, 范恩,等. 受恶意程序传染的WSNs可生存性评估[J]. 传感技术学报, 2016, 29(7): 1083- 1089.

[6] Wang X, He Z, Zhang L. A pulse immunization model for inhibiting malware propagation in mobile wireless sensor networks[J]. Chinese Journal of Electronics, 2014, 23(4): 810- 815.

[7] 曹玉林, 王小明, 何早波. 移动无线传感网中恶意软件传播的最优安全策略[J]. 电子学报, 2016, 44(8): 1851- 1857.

[8] 孙凌. 社交网络中的信息与影响力传播模式研究[D]. 北京交通大学, 2017.

[9] Chen X, Kim K T, Youn H Y. Integration of Markov Random Field with Markov Chain for Efficient Event Detection using Wireless Sensor Network[J]. Computer Networks, 2016, 108:108- 119.

[10] Yu Q, Jiang W, Leng S, et al. Modeling wireless sensor network based on non-volatile cellular automata[J]. IEICE Transactions on Communications. 2015, 98(7):1294- 1301.

[11] Roy S, Karjee J, Rawat U S, et al. Symmetric Key Encryption Technique: A Cellular Automata based Approach in Wireless Sensor Networks[J]. Procedia Computer Science, 2016, 78: 408- 414.

[12] 赵焱鑫. 移动自组网病毒传播模型及稳定性研究[D]. 陕西师范大学, 2015.

[13] 胡金涛, 宋玉蓉, 苏晓萍. 有向天线的无线传感器网络病毒传播模型[J]. 计算机科学, 2016, 43(5): 127- 131.

[14] 沈士根, 刘建华, 曹奇英. 博弈论与无线传感器网络安全[M]. 清华大学出版社, 2016.

[15] 沈士根, 周海平, 黄龙军, 等. 基于最优反应均衡的传感网恶意程序传播抑制方法[J]. 传感技术学报, 2017, 30(10):1589- 1595.

[16] Shen S, Li H, Han R, et al. Differential game-based strategies for preventing malware propagation in wireless sensor networks[J]. IEEE Transactions on Information Forensics and Security, 2014,9(11):1962- 1973.