基于增量贝叶斯学习模型的在线电路故障诊断

李梦婷 赵 帅 陈绍炜 黄登山(西北工业大学电子信息学院 陕西 西安 710072)

0 引 言

人们生活的方方面面都与“电”有着密不可分的关系，电路的安全与稳定直接影响着人们的生活质量，而电子设备和系统随着使用会逐渐损坏，对于电路故障的检测就显得尤为重要。对电路故障的诊断，一般需要根据搜集到的历史数据，统计出所有可能发生的故障，及故障发生时的电路特征，建立一个故障诊断的模型。当电路再次发生故障时，提取此时的电路特征，将电路特征数据输入故障诊断模型，对此时发生的故障进行分类。

由前人已做的研究可知，比较常用的分类算法有支持向量机SVM、神经网络、KNN、贝叶斯算法等。Mandava等[1]证明了SVM算法在模拟电路故障诊断中具有良好的诊断精度，并提出应在更加复杂的模拟电路进行验证这一算法的优点。Abed 等[2]将离散小波变换特征提取方法和一系列降维处理方法与神经网络方法相结合，能有效应用于轮转电机的故障诊断当中。Appana等[3]将一种密度加权距离相似度度量和KNN算法相结合，并将所提算法应用于滚动轴承故障诊断中，实验证明KNN算法能有效识别滚动轴承的故障类型。朴素贝叶斯算法在分类领域应用十分广泛，分类精度方面也能与其他传统分类算法媲美。Pratama等[4]就利用朴素贝叶斯算法、KNN算法和支持向量机算法分别根据推特用户的发文预测用户人格，实验表明朴素贝叶斯算法在对人格预测的过程中表现略优于其他方法。

传统故障诊断方法应用于在线电路故障诊断中，往往是结合新增的故障样本对诊断模型重新学习，虽然诊断精度随新增样本的增加逐步提高，但重新学习的过程耗时很长，不能及时报出诊断结果，无法满足在线故障诊断的实时性要求[5]。将传统的故障诊断算法与增量学习相结合，能一定程度上减少学习时间，提高模型更新速度。由于朴素贝叶斯算法数学逻辑性强，与其他算法相比，用于增量学习更能有效地对模型进行更新。

基于以上分析，以及在线电路故障诊断对诊断精度和模型更新速度的要求，本文提出了基于增量式贝叶斯学习的在线电路故障诊断方法。该方法结合了贝叶斯算法和增量学习的思想，利用新增样本通过相关概率更新公式对模型进行更新，而不用保存原始数据，节省了大量的存储空间，大大提高了模型更新速度。除此之外，在处理特征属性数据时，采用了核函数主成分分析KPCA对数据进行降维，简化了运算，进一步提高了模型的运行速度。在诊断精度方面增量式贝叶斯算法能达到与传统的批量式贝叶斯算法的近似水平，且增量式贝叶斯分类器的模型更新速度快、实时性高。因此，现实在线电路故障诊断中该算法十分实用，后文将利用电路进一步说明。

1 算法分析

1.1 朴素贝叶斯分类模型

朴素贝叶斯分类模型是以贝叶斯原理为基础，各项特征属性独立为前提，结合类先验概率和各特征属性条件概率计算后验概率的模式识别方法[6]。

在电路运行过程中，各种故障出现的概率是可估计的，可以根据经验或先前所得的数据得到电路系统的故障类型，每一个故障发生时都有相应的特征信息，采集这些故障及其对应的故障特征作为数据样本。每个数据样本都可以用特征向量T和类别变量c表示，假定一个m维向量T由{t1,t2,…,tm}组成，m个特征项之间相互独立，类别变量c有n种取值，分别是(c1,c2,…,cn)，则每个数据样本可表示为〈T,c〉。根据贝叶斯定理，在已知先验概率P(ci)、条件概率P(T|ci)以及边缘概率P(T)时，可以根据贝叶斯公式：

(1)

求出各类别变量c1,c2,…,cn对应的后验概率P(c1)|T)，P(c2|T)，…，P(cn|T)，从中找出最大的后验概率，其对应的类别ci即为该数据样本的故障标签[7]。一般的，在作比较时，边缘概率P(T)是不变的，所以考虑P(ci)·P(T|ci)的大小就可以了。

采用拉普拉斯估计[8]，得到类先验概率式(2)和各特征属性条件概率式(3)：

(2)

(3)

式中：|Dci|表示训练样本中属于类别ci的样本数量；|C|表示故障标签的种数；|D|表示训练集样本数；|Dtk|ci|表示训练样本中属于ci类的含有属性值tk的样本数；|Bk|表示训练样本中第k个特征属性的取值个数。

由各特征相互独立，可得：

(4)

根据训练样本数据，由式(2)可以求出类先验概率P(ci)；由式(3)可以求出各个特征属性的条件概率P(tk|ci)，进而求出条件概率P(T|ci)。

朴素贝叶斯分类器具有数学逻辑力强，分类精度高的优点[9]。但传统的朴素贝叶斯分类器存在以下两个问题：1) 分类器的分类精度与训练集的大小和数据的完备性密切相关，但一般难以获得一个完备的训练集；2) 用于在线电路故障诊断时，样本数据逐步积累，而每增加一批样本数据，就要重新计算一次类先验概率和各特征属性条件概率，耗费大量时间，不能满足在线电路故障诊断的实时性要求。而将贝叶斯算法和增量学习相结合能在保存其固有的强逻辑性和高诊断精度的同时很好地解决以上这些问题。

1.2 增量式贝叶斯分类模型

故障再次发生，将新增样本数据输入贝叶斯分类模型，得到该样本的故障类型。若对此故障的判断是可靠的，则可将该样本用于更新模型，数据集将趋于完备，模型的诊断精度也随之提高[10]。处理新增数据样本时，传统的贝叶斯分类模型是进行批量学习，根据训练集和新增样本重新计算类先验概率和特征属性条件概率，此方法运算量大、耗时长，不能满足在线电路故障诊断的实时性要求。而本文提到的增量式贝叶斯分类模型只需通过少量运算即可更新模型。增量式贝叶斯学习的流程如图1所示。

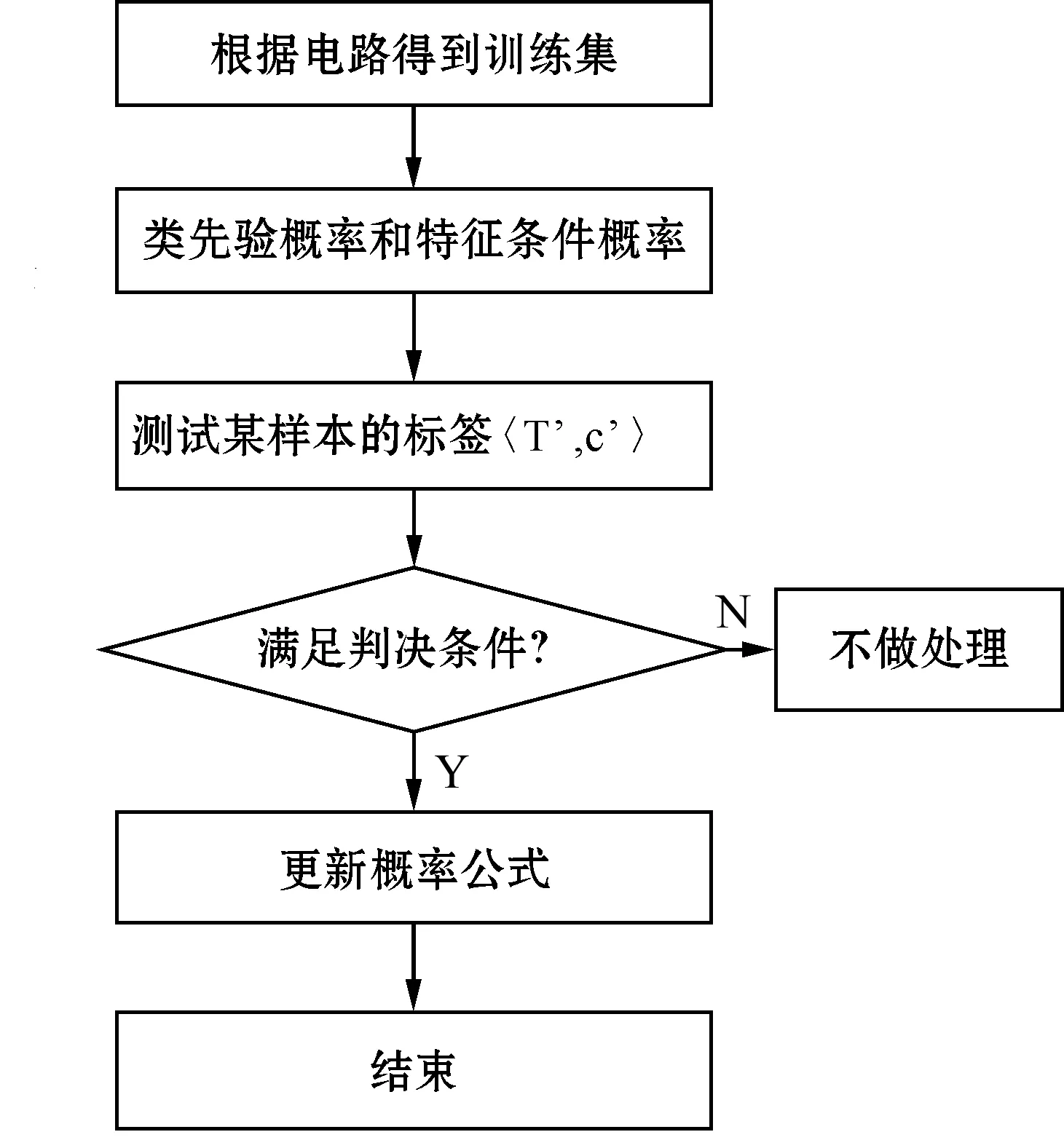
图1 增量式贝叶斯学习流程图

对于新增样本，先判断其故障类型，当满足判决条件时，该样本可用于更新模型，即更新类先验概率概率和特征属性条件概率，公式如下：

(5)

(6)

式中：P*(ci)是更新后的类先验概率，P*(tk|ci)是更新后的各特征属性的条件概率。式(5)、式(6)可简化如下：

(7)

(8)

式(7)、式(8)中，δ=|C|+|D|，ζ=|Bk|+|Dci|，式(7)为类先验概率更新公式，式(8)为特征属性条件概率更新公式。

(9)

2 增量式贝叶斯在线故障诊断中的应用

本文在Multisim仿真环境中以双二阶RC有源滤波器电路(如图2所示)作为实验对象，比较增量式贝叶斯学习和批量式贝叶斯学习在在线电路故障诊断中的诊断精度和运算量。在此电路中，信号源是幅值为1 V，频率为10 Hz的正弦信号，C1=C2=10 nF, R1=R2=R3=R4=R5=R6=10 kΩ，R1、R2、R3、R4、R5、R6的容差设置为5%，C1、C2的容差设置为10%。本实验仅考虑单一故障。

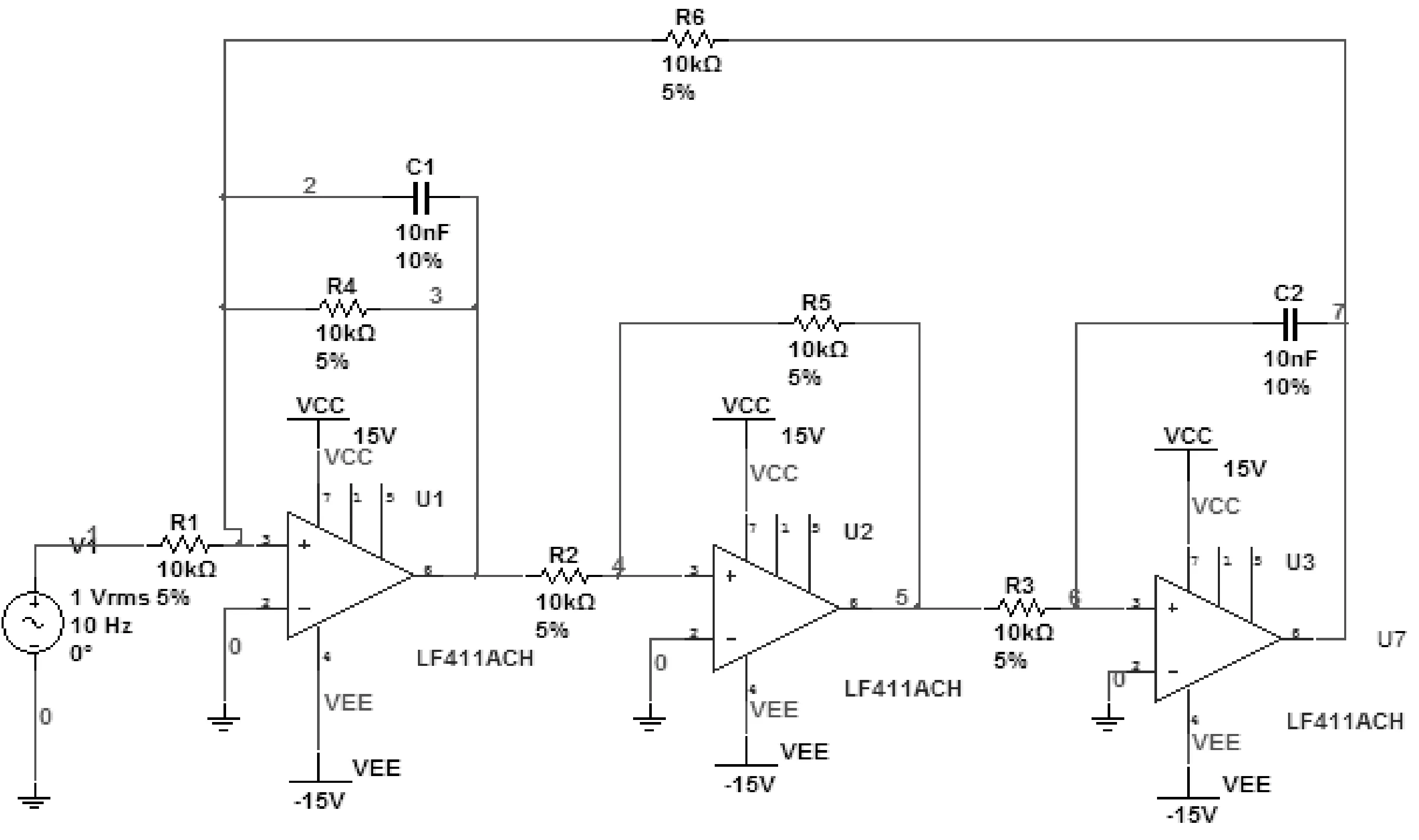
图2 双二阶RC有源滤波器

本文中增量式贝叶斯学习用于上述电路在线故障诊断的整体流程如下。

步骤1：确定此电路系统的所有可能发生的故障类型，本文通过找出此电路中对输出影响较大的敏感元器件，将这些敏感元器件作为故障点，由此确定所有的故障类型。

步骤2：提取每一故障模式下的特征属性，并对特征属性数据进行降维。

步骤3：选择合适的训练集大小，以便获得更好的实验效果。

步骤4：训练贝叶斯分类模型，计算诊断精度。

步骤5：利用满足条件的新增样本根据式(7) 、式(8)更新模型，即更新故障类型的类先验概率和各特征属性的条件概率。

步骤6：计算更新后模型的诊断精度，及步骤5更新模型耗时。

对双二阶RC有源滤波器电路进行灵敏度分析，以确定其敏感元器件，其交流灵敏度分析如表1所示。其中X1表示每个元器件参数的变化量，Y1表示输出电压U7对应的变化量。

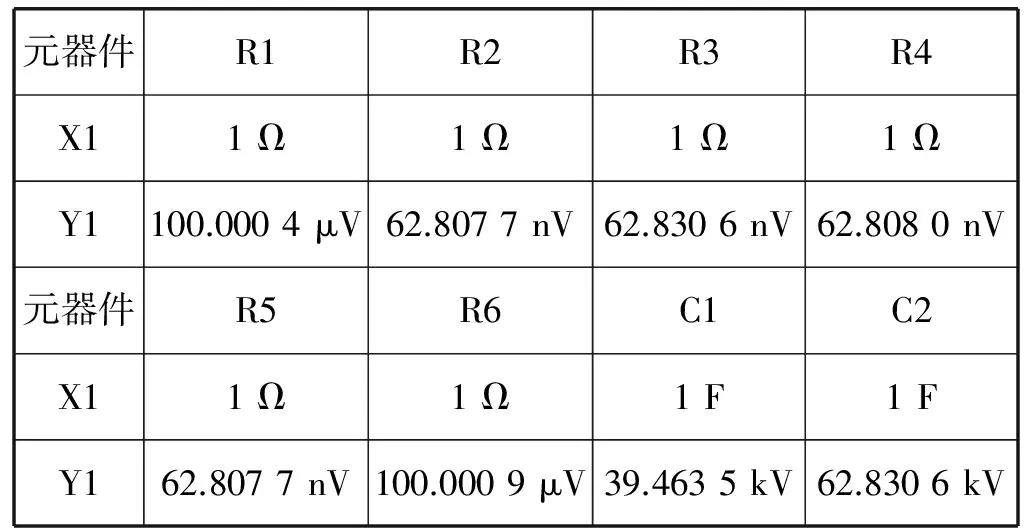
表1 交流灵敏度分析

由表1可以看出各个元器件每变化一个单位对输出电压U7的影响大小，进行对比之后确定了C1、C2、R1、R5、R6这五个对输出电压影响较大的元器件作为故障点。分别取这五个元器件标称值的 ±50%作为故障值，共有10种故障模式，分别表示为F1-F10，正常工作的模式表示为F0，故障及参数设置如表2所示。

表2 故障设置

为了提取每个工作模式下的电路特征，在11种工作模式中，以U7作为输出电压，在0.1 s内进行50次蒙特卡罗分析。图3展示的就是11种工作模式下对输出电压U7进行50次蒙特卡罗分析的结果。通过对这11种工作模式下的50次蒙特卡罗分析，可以得到550组特征属性为100维的数据样本。

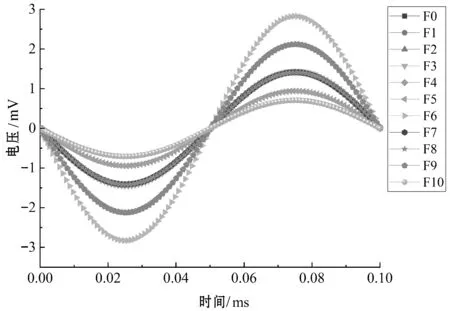
图3 11种模式下50次蒙特卡罗分析图

用550组100维的数据进行故障诊断，不仅运算量非常大，诊断精度也会受到严重影响。为了解决样本数据维数造成的问题，本文采用径向基核函数主元分析去除冗余项，降低样本数据的维度。径向基核函数主元分析是KPCA的一种。KPCA是一种非线性主元分析[13]，通过非线性映射将由50次蒙特卡罗分析得到的550组矢量样本数据映射到一个高维空间，使得这550组矢量样本数据具有很好的可分性，然后再对映射到高维空间中的数据进行线性主元分析[14]，从而将这550组样本数据降到三维。经KPCA降维后550组数据样本在三维空间分布如图4所示。

图4 数据样本三维分布图

图中用11种不同形状的点表示了11种工作模式对应的样本，从图中可以看出经过KPCA降维后的样本点在三维空间中具有很好的可分性，大大简化了运算并提高了诊断精度。

在经过KPCA降维后的550组三维样本数据中，随机取出其中的N组样本作为训练集，为了充分展现实验效果，增量集和测试集应包含较多样本，因此取其中的500组样本作为增量集以及测试集，测试集主要用于检测处于不同阶段的分类器的准确率，作为分析诊断模型性能的指标之一。

训练集的大小和完备性对分类器的准确性有很大的影响[15]。显然，训练集越完备，分类器模型的准确性也越好；反之，分类器的准确性将降低。为了均衡考虑分类器的准确性和运算量，使实验结果更加可靠，先做一组试验，确定N合适的取值。

分别在550组样本中随机取30、40、50、60、70、100、550组样本作为训练集，在550组样本中取定500组样本作为增量集和测试集，通过仿真结果分析不同训练集训练的分类器在增量的各阶段准确率的走势，可以依次判断训练集大小对分类器性能的影响。仿真结果如图5所示。

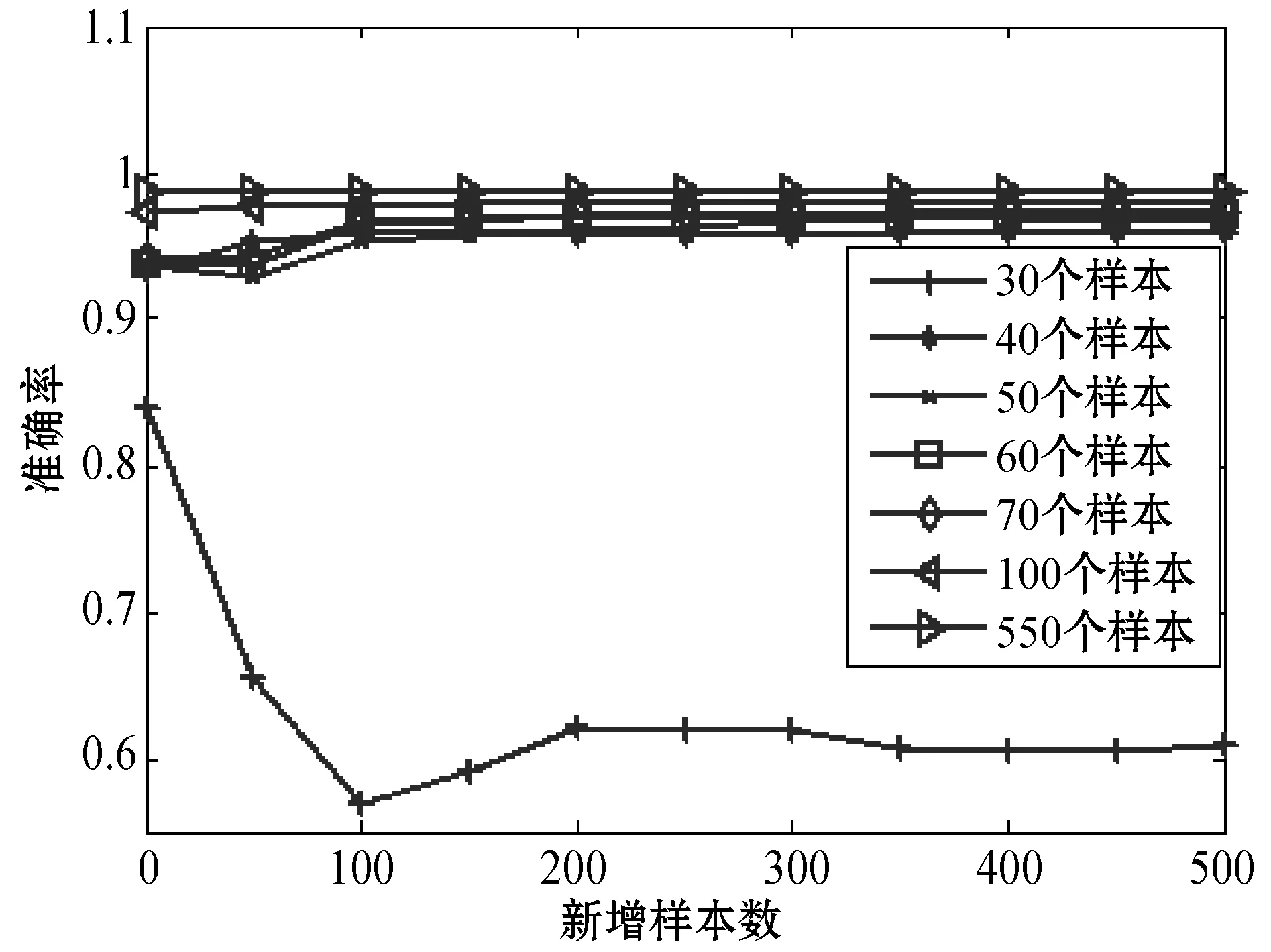
图5 不同训练集仿真结果

从图5中可以看出各训练集产生的诊断模型的准确率趋势，除了含30和550组样本的训练集，其余训练集产生的诊断模型的准确率均呈上升趋势，表3中列出了具体的实验数据。其中，Percent1表示增量前诊断模型的准确率，Percent2表示增量后诊断模型的准确率。

表3 不同大小训练集的准确率

从表3中可以看出，训练集样本数量取30时，因为训练集数据不够全面，导致分类器准确性整体呈下降趋势，不符合实验要求。当训练集样本数取得较大时，例如100和550，增量前诊断模型的准确率已达到较高水平，增量前后准确率的改变量很小甚至没有，用于增量实验不能说明问题。可以看到当训练集样本数量取在40至70之间时，故障诊断的准确率较高，且随着增量学习，准确率呈上升趋势，准确率的变化约在2.6至3.4个百分点。其中当训练集的样本数取60个，增量前后准确率对比最为明显。基于以上的实验分析，本文采用第4组的实验结果，取训练集的样本数为60个，增量集和测试集样本数为500个。

为了降低运算的复杂性，每增量50个样本检测一次诊断模型的准确率。仿真得到增量式贝叶斯学习和批量式贝叶斯学习用于图2电路在线故障诊断的准确率和运算量，并进行比较。

对于传统的批量式贝叶斯机器学习，先用含60组样本数据的训练集建立故障诊断模型，并用测试集检测模型的准确率。根据传统贝叶斯机器学习的原理，用增量集中的样本数据，每增加一组样本数据更新一次模型，诊断模型的参数全部重新计算一次， 然后每增加50组样本计算一次模型的准确率。

对于本文提出的增量式贝叶斯机器学习，用含有相同的60组样本数据的训练集建立贝叶斯模型，并用测试集检测模型的准确率。利用增量集中的样本数据，每增加一组样本数据，根据概率更新式(7)、式(8)，更新一次诊断模型概率参数，实验中发现将判决条件中的α值设置为0.6最为合适。同样每增加50组样本计算一次模型的准确率。其中两种学习方法的运算量用每增加一组样本更新模型所耗的时间表示。

本实验基于Matlab仿真平台，得到仿真结果如图6所示，其中，(a)表示增量贝叶斯学习和批量贝叶斯学习的准确率对比，(b)表示增量贝叶斯学习和批量贝叶斯学习的耗时对比。

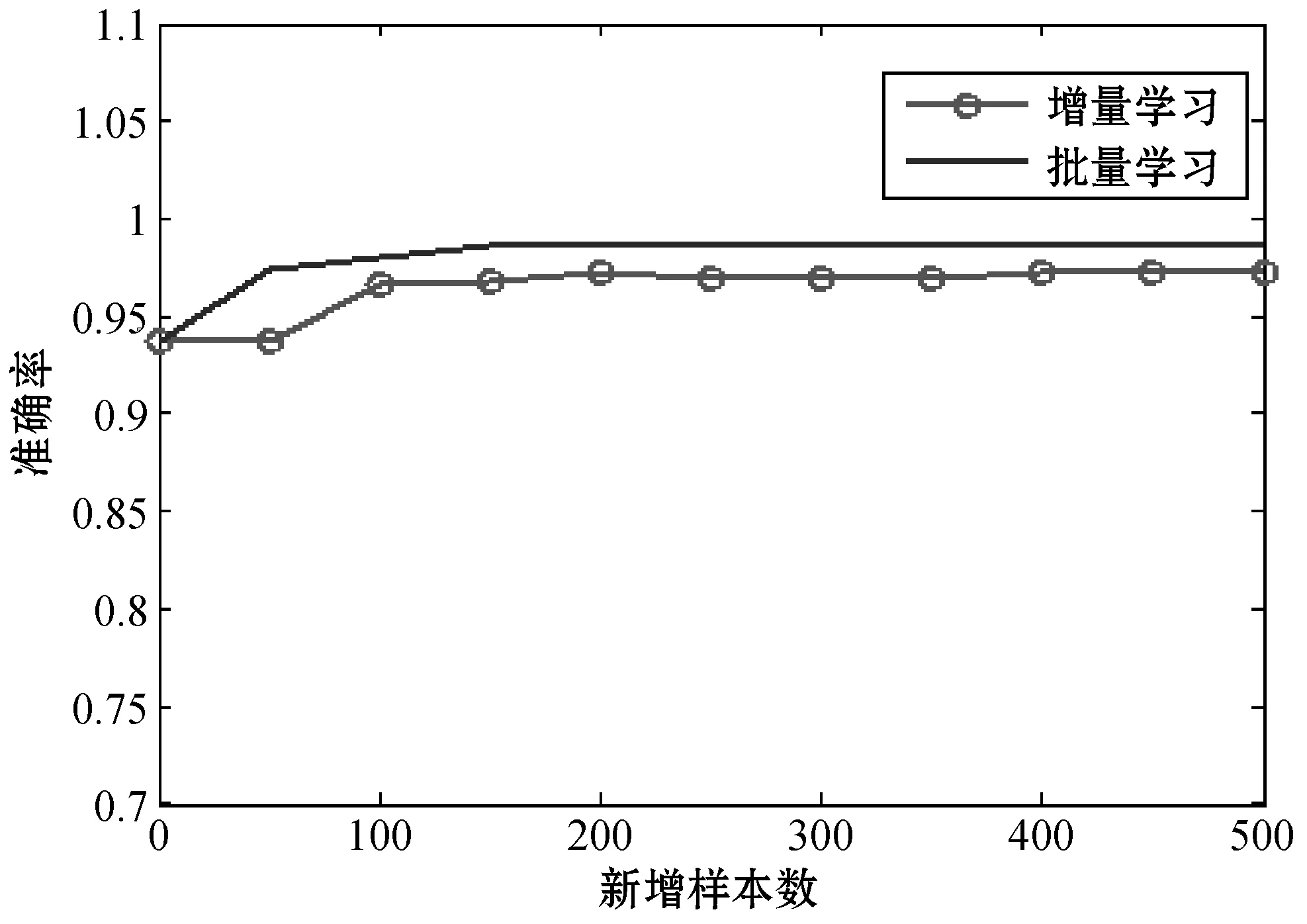
(a) 准确率对比

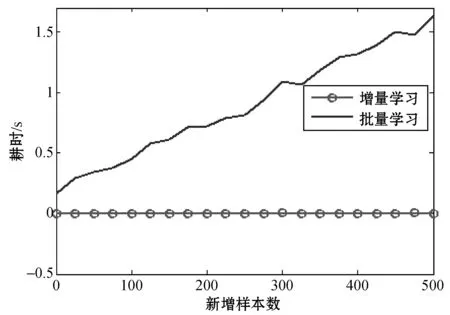
(b) 耗时对比图6 增量贝叶斯和批量贝叶斯性能对比

从图6可以看出，经过500个样本的增量，批量式贝叶斯诊断模型的准确率从93.80%上升至98.80%，上升了5.0个百分点，增量式贝叶斯诊断模型的准确率从93.80%上升至97.20%，上升了3.4个百分点。随着新增样本的加入，两种方法都能逐步提高诊断模型的诊断精度，在准确率方面两种方法与贝叶斯算法相比都表现出相对的优势，而且批量式贝叶斯诊断模型和增量式贝叶斯诊断模型的最终准确率相差1.6个百分比，两者准确率性能近似。运算量方面可以看到，增量贝叶斯诊断模型每新增一组样本更新模型所耗时间非常短，基本维持在0.01 s以内，即每更新一次模型增量式贝叶斯诊断模型的运算量非常小；而批量贝叶斯诊断模型从最初的0.170 0 s逐渐上升至1.640 0 s，并有继续上升的趋势。可见随着累积样本的增多，每增加一组样本，批量式贝叶斯诊断模型更新一次模型所耗的时间越来越长，运算量越来越大；而增量式贝叶斯诊断模型的运算量一直维持在很低的水平。

3 结 语

本文提出一种实时性高的在线电路故障诊断方法，即以增量式贝叶斯算法为基础，并结合KPCA方法对特征数据进行降维的方法。将该方法运用于双二阶RC有源滤波电路。实验证明，与传统的批量式贝叶斯算法相比，本文所提方法更新模型时仅需通过较小的运算量即可对类先验概率和各特征属性条件概率进行更新，即模型更新，使得本文所提方法能够在保证诊断精度与批量式贝叶斯算法近似的同时，大大降低了模型更新的时间，能够满足在线电路故障诊断过程的实时性和准确性要求。在实际在线电路故障诊断中，新增样本的故障可能是不同于训练模型前统计所得的所有故障的新一类故障，对于这种故障的处理将是后期继续研究的内容。

[1] Mandava M S, Jadhav D, Naik R R. Fault classification using SVM[C]// Circuits and Systems Symposium. IEEE, 2016:17- 21.

[2] Abed W. Neural network fault diagnosis of a trolling motor based on feature reduction techniques for an unmanned surface vehicle’[J]. Proceedings of the Institution of Mechanical Engineers Part I Journal of Systems & Control Engineering, 2015, 85(5):227- 251.

[3] Appana D K, Islam M R, Kim J M. Reliable Fault Diagnosis of Bearings Using Distance and Density Similarity on an Enhanced k-NN[M]// Artificial Life and Computational Intelligence. Springer International Publishing, 2017:193- 203.

[4] Pratama B Y, Sarno R. Personality classification based on Twitter text using Naive Bayes, KNN and SVM[C]// International Conference on Data and Software Engineering. IEEE, 2016:170- 174.

[5] Ade R, Deshmukh P R. Classification of students by using an incremental ensemble of classifiers[C]//International Conference on Reliability, INFOCOM Technologies and Optimization. IEEE, 2015:1- 5.

[6] 许明英,尉永清,赵静.一种结合反馈信息的贝叶斯分类增量学习方法[J].计算机应用,2011,31(9):2530- 2533.

[7] Hooten MB,Hobbs NT.A guide to Bayesian model selection for ecologists[J]. Ecological Monographs,2015, 85(1):3- 28.

[8] 王小林,镇丽华,杨思春,等.基于增量式贝叶斯模型的中文问句分类研究[J].计算机工程,2014,40(9):238- 242.

[9] 李杨.基于增量贝叶斯模型的自助挂号系统研究[D].北方工业大学,2016.

[10] 黄金龙.基于贝叶斯网络的语音情感识别[D].华南理工大学,2014.

[11] 罗福星.增量学习朴素贝叶斯中文分类系统的研究[D].中南大学,2008.

[12] Dimkovski M,An A.A Bayesian model for canonical circuits in the neocortex for parallelized and incremental learning of symbol representations[J].Neurocomputing, 2015,149(4):1270- 1279.

[13] Li Z,Kruger U,Xie L,et al.Adaptive KPCA Modeling of Nonlinear Systems[J].IEEE Transactions on Signal Processing,2015,63(9):2364- 2376.

[14] 汪司飞,黄斐.基于K-均值聚类的KPCA在故障诊断中的应用[J].计算机应用与软件,2013,30(4):120- 123.

[15] Hu Yinhui,Chen Lin.Incremental learning method for fault diagnosis in large-scale InfiniBand network[J]. Journal of Computer Applications, 2015, 35(11): 3092- 3096.