聚合物粘结剂PVP、PAM和PVA结构与性能的分子动力学研究
2018-07-04,,,,,
, , , , ,
(西北工业大学 机电学院,西安 710072)
1 引 言
随着三维打印技术的发展,基于微滴喷射原理的三维粉末粘结打印技术已在很多领域得到应用,特别是在骨支架制备方面技术已比较成熟[1,2]。该技术主要是通过打印喷头喷射胶水,使胶水铺展在粉末材料的表面,从而实现粉末材料的粘结成型。其结合了快速成型技术的特点,在计算机的辅助下可以实现任意结构复杂零部件的制造,因此该技术在人工骨支架的生物制造领域有着极其重要的作用。但是,基体材料的选择一直是阻碍该技术广泛应用的主要因素,因为骨支架植入体内不仅会与人体组织直接接触,还需要暂时起到支撑人体组织和器官的作用,所以材料必须具有一定的生物相容性及力学性能。目前,羟基磷灰石HA(Hydroxyapatite)因其具有优良的生物相容性、骨传导性以及与天然人骨相类似的化学成分,是制备人工骨最为理想的材料。因此,制备工艺中粘结剂的选择成了人工骨支架制备的关键。当前使用最多的是酸性粘结剂,因为酸性粘结剂能与HA界面发生一系列的化学反应,使制备的骨支架具有较好的力学性能[3,4]。但是酸性粘结剂会给骨支架带来污染,带酸性的骨支架植入体内后很容易引起周围组织的炎症和排异。解决这一问题最有效的方法是先采用聚合物粘结剂制备骨支架雏形,然后再使用酸性粘结剂或者其他粘结剂进行固化处理。然而,该方法还存在很多的不确定因素,特别是内部的微观结构和力学性能。在粉末粘结三维打印骨支架的制备过程中,液滴与粉末的相互作用决定了骨支架制件的微观结构和宏观机械性能[5],由于HA陶瓷材料的力学性能远高于聚合物粘结剂,所以聚合物粘结剂的力学性能对骨支架的机械强度起着决定性的作用,研究粘结剂的基本性能对骨支架的制备工艺具有十分重要的意义。而最为常用的三种聚合物粘结剂为聚乙烯毗咯烷酮PVP(polyvinylpyrrolidone)、聚丙烯酰胺PAM Polyacrylamide和聚乙烯醇PVA(polyvinyl alcohol),主要是因为这三种粘结剂具有良好的生物惰性和生物相容性,并且不会给HA带来污染。
粘结剂的微观结构及其与HA的相互作用是一种微观现象,通过传统实验方法很难实现观察和研究。而分子动力学MD(molecular dynamics)模拟方法是研究高分子与无机盐材料界面相互作用的一种最有效的方法[6]。MD是一种基于原子力场的计算方法,能够模拟不同物质之间的力学及电学等性质,计算空间距离从几个埃到几个纳米,可以准确解释物质之间的相互作用机理。目前该技术已经在很多领域得到了成熟的运用[7,8],其中围绕HA展开的研究也有很多,Zhang等[9]利用MD模拟研究了在没有耦合剂作用的条件下,人工骨组成材料羟基磷灰石与复合材料界面的相互作用,比较分析了聚合物在三个不同平面的约束能,对人工骨制造具有一定的指导作用。潘海华等[10]研究了人工骨材料羟基磷灰石HA晶面上的水分子行为,发现HA晶面附近的结构化水层可阻止溶液离子自由进入晶面,对HA颗粒在水溶液中的动力学稳定性具有重要影响。李敏等[11]利用MD技术研究了HA及复合材料的制备与性能,特别是人工骨的制备工艺及弹性模量的研究对生产制造意义重大。
本文主要借助分子动力学方法对骨支架制备工艺中常用三种聚合物粘结剂聚乙烯毗咯烷酮PVP、聚丙烯酰胺PAM和聚乙烯醇PVA的结构和性能进行研究,从分子层面对粘结剂的相关性质进行了预估,为骨支架3D打印工艺制备工艺中胶水的选择提供理论指导。
2 模型的建立与模拟方法
对于高分子聚合物体系的模拟仿真,合适聚合度的选取尤为重要,关系到模拟结果的准确性。为了确定聚合物分子链的聚合度,本文根据三种粘结剂的分子结构式构建不同聚合度的分子链模型,如图1所示。对构建的不同重复单元数的三种粘结剂分子链Smart minimizer 方法进行优化,使其能量最小化,当迭代能量达到0.001 kcal/mol时停止计算。然后对所建模型进行热处理,(1) NVT系综下分子动力学模拟,模拟温度以50 K为步长从298 K逐渐升到598 K,然后从598 K又逐渐降到298 K,每步计算50 ps;(2) NVT系综下分子动力学模拟,在298 K的温度下对步骤(1)的最后结构进行200 ps的NVT分子动力学模拟,从而得到室温下高分子链的平衡结构。最后,对平衡结构进行数值分析,得到高分子链的内聚能密度,并根据粘结剂的内聚能密度变化来确定合适的聚合度选择范围。此外,聚合度的选择还必须满足每条粘结剂高分子链的分子量接近,这样才能使其具有可比性,详细的计算过程可以参考文献[12]。
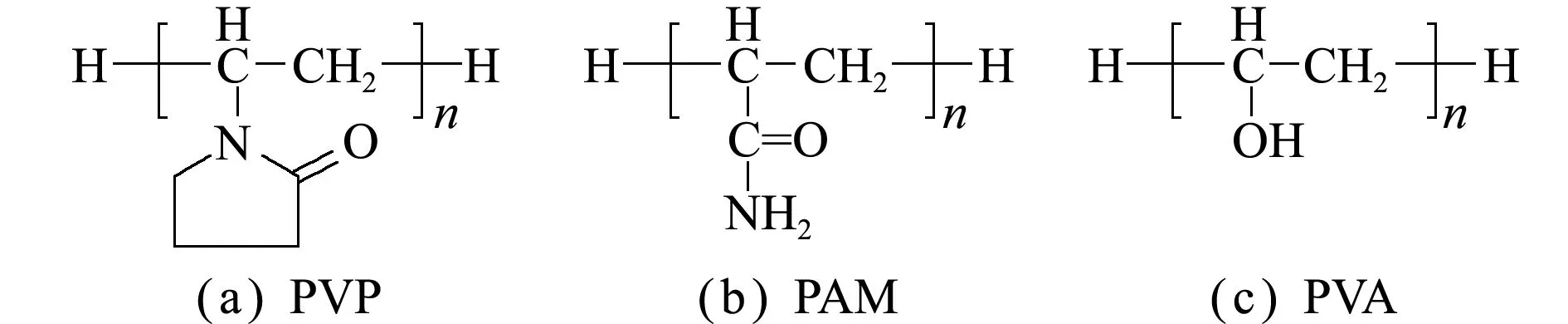
图1 PVP,PAM和PVA粘结剂的分子结构式
Fig.1 Molecular structural formula of PVP,PAM and PVA
本文PVP,PAM和PVA三种粘结剂分子链选取的聚合度分别为20,31和50,为了对三种粘结剂的基本性能进行计算,分别建立了三种粘结剂的计算模型,模型的能量最小化过程同上面分子链的优化过程一致。然后,对能量最小化的三种分子模型进行分子动力学模拟,模拟过程如下。(1) NPT系综模拟,模拟时间为200 ps,或者待密度达到平衡后停止计算。(2) NVT系综模拟,模拟时间为50 ps,并对该过程的轨迹文件进行数值分析。最终平衡后的分子模型如图2所示。
所有分子动力学过程均是在COMPASS[13]力场下进行。且在模拟中,采用Andersen恒温器[14],用Velocity Verlet积分法求解牛顿运动方程,原子初始速度按Boltzmann随机分布方法确定。计算采用的时间步长为1 fs,模拟过程中每500步记录一次体系的轨迹。模拟过程中Vander Waals和Coulomb分别按Atom based[15]和Ewald[16]方法计算,截断半径为9.5 Å,样条宽度取1 Å,缓冲宽度取0.5 Å,温度设置为298 K。
3 结果和讨论
计算模型达到平衡是研究材料性质的前提,关系到计算结果的可靠性。判断体系是否达到平衡所依据的参数一般有能量、温度、密度以及径向分布函数等[17]。本文采用最常用的密度和能量来判断体系的平衡,在体系密度和能量等围绕一恒定值发生微小波动时,认为体系达到了平衡。PAM优化后体系的密度和能量的变化曲线如图3所示。可以看出,经过NPT分子动力学优化后,模拟体系已达到了平衡。

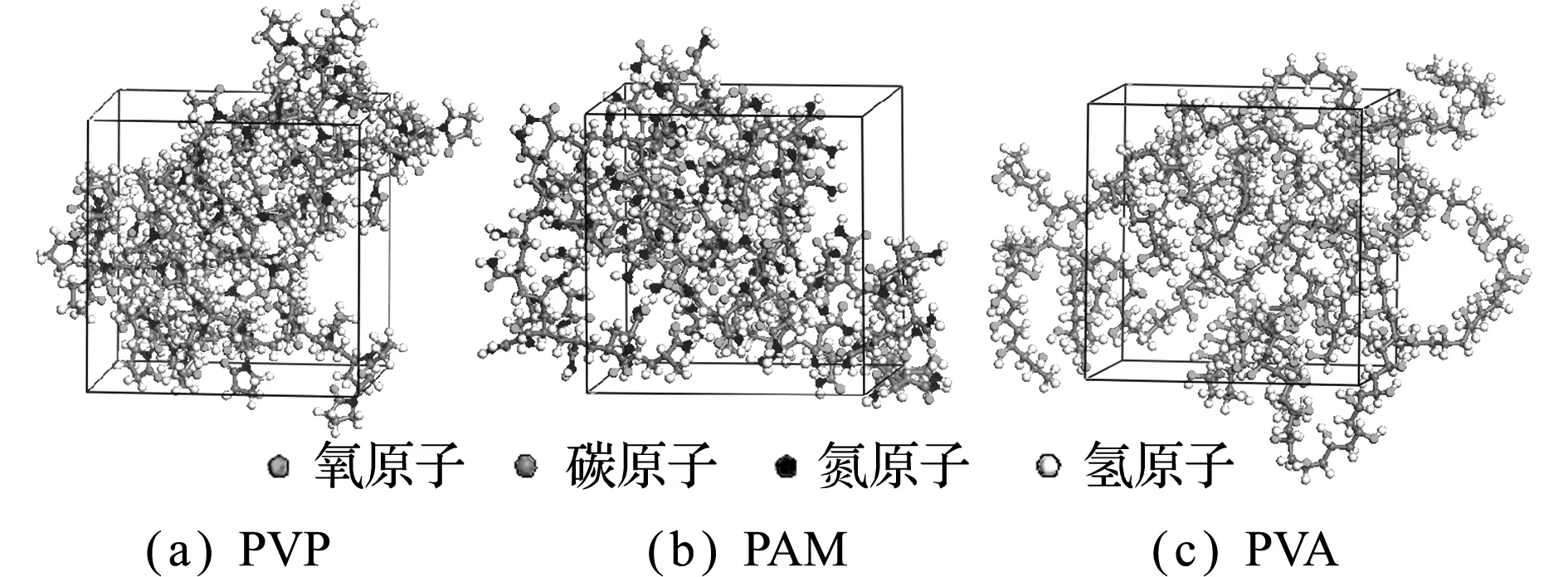
图2 三种粘结剂的平衡分子模型
Fig.2 Equilibrium models of three binders
内聚能密度CED(Cohesive Energy Density)是表征高分子材料的一个重要参数,是评价分子间作用力大小的一个物理量,主要反映分子基团间的相互作用。凡与物质间相互作用有关的性质和物性属性与内聚能密度都具有内在联系,如物质的溶解性、粘度和相容性等,其表达式为
CED=Ecoh/v
(1)
式中Ec oh指内聚能,v为物质的量混合体积。一般来说,分子中所含基团的极性越大,分子间的作用力就越大,则相应的内聚能密度就越大。
从图4三种粘结剂内聚能的计算结果可以看出,三种粘结剂内聚能的大小关系为PAM>PVA>PVP,PAM的内聚能密度最大,PVP的内聚能密度最小。而CED的大小可以反映体系内部分子间相互作用的强弱,即内聚能密度越大,体系内部分子间相互作用力越大。因此,三种高分子粘结剂
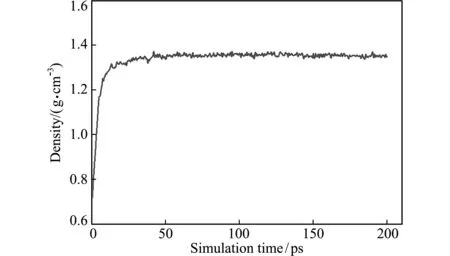
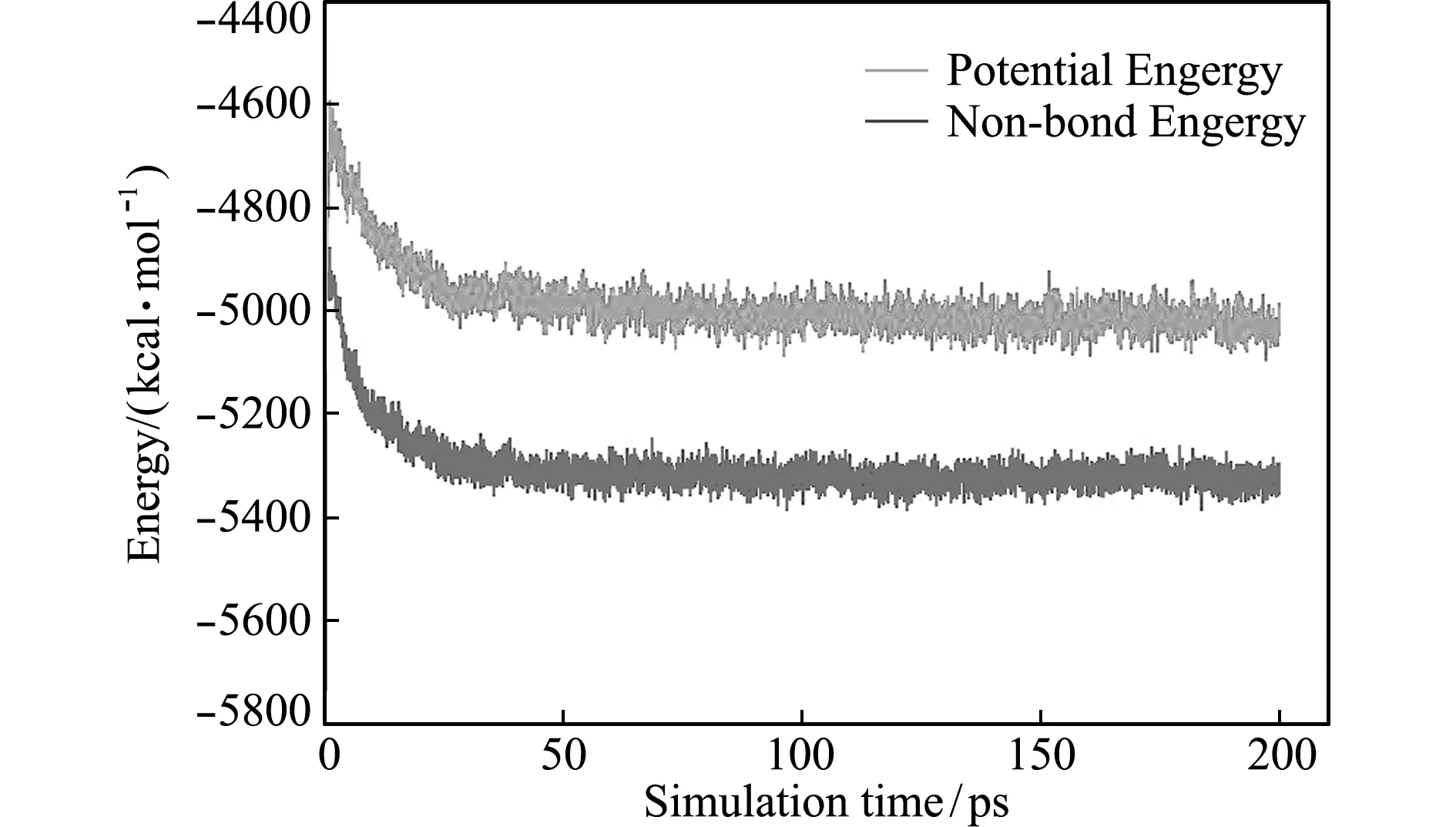
图3 PAM无定形晶胞体系密度和能量随模拟时间的变化曲线
Fig.3 Plot of the density and total potential energy,nonbond energy of PAM binder system as a function of MD simulation time
体系内部相互作用力的大小关系为PAM>PVA>PVP,这与平衡结构密度的计算结果一致。
力学性能是粘结剂材料的重要性能之一,因为在骨支架的粘结打印工艺中,粘结剂的力学性能直接关系到所制备骨支架的力学性能。本文通过对体系平衡结构进行静态力学性能分析来计算粘结剂的力学性能,如弹性系数、模量和泊松比等。在原子水平计算中,静态模型计算内应力张量σ[18]采用的是维里方程:
(2)
式中mi和Vi分别为原子的质量和速度,V0为无形变时的体积。
弹性系数矩阵由数值法求解相应应力与应变的一阶导数而得到,采用最小二乘法拟合求得拉伸模量E和泊松比γ,进而可求得其他有效的各向同性力学性能,如剪切模量G、体积模量K及柯西压(C12-C44)等。对于各项同性材料,其模量可用拉梅参数表示为
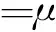
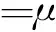
(3)
通常材料的硬度与其拉伸模量E和剪切模量G密切相关,其值越大,材料的刚性和硬度越高。材料断裂强度的大小由体模量K度量,K值越大,表明材料的抗断裂能力越大。柯西压通常用来预估体系的延展性,若为负值则材料显脆性,若是正值则表明材料延展性较好,其值越高表明体系的延展性越好[19]。
由表2可知,三种粘结剂的力学性能存在一定的差异,且三种粘结剂模量和柯西压值的大小关系表现一致,都为PVA>PVP>PAM,也就是说相对于PVP和PAM,PVA的力学性能较好。该计算结果与粘结剂的内聚能结果不一致,说明粘结剂的力学性能与内聚能密度和质量密度不存在特定的关系。此外,三种粘结剂的泊松比都在塑料的泊松比范围之内,表明三种粘结剂具有一定的塑性。同时,柯西压值都为正值,说明三种粘结剂都具有一定的延展性,且PVA的延展性最好,PAM最差。

图4 三种粘结剂的内聚能柱状图
Fig.4 CED Histograms of three polymer binders
为了进一步探索粘结剂在生物陶瓷表面的粘结行为,建立了三种粘结剂在羟基磷灰石HA(hydroxyapatite)界面的相互作用模型,所选HA界面是表面原子密度最大的HA(110)界面[5]。所建计算模型的平衡构型如图5所示,该模型的分子动力学计算模拟过程与粘结剂体系的模拟细节类似。
表2 粘结剂在298 K温度下的力学性能
(单位:GPa)
Tab.2 Mechanical properties of binders at 298 K(unit:GPa)

SystemPVPPAMPVAC119.535.7715.99C228.546.0814.23C337.354.5614.95C441.802.392.23C552.912.763.64C662.392.124.02C124.504.277.89C133.873.557.16C233.163.5810.25C15-1.140.84-0.27C25-0.650.32-0.62C350.17-0.480.12C46-0.20-0.190.13Tensile modulus6.814.289.22Bulk modulus5.273.588.09Shear modulus2.651.653.41Poisson ratio0.280.290.31C12-C442.701.885.66
高分子粘结剂与生物陶瓷间的粘结力大小可以通过材料间界面结合能的大小来反映,界面结合能越大,表示粘结剂与生物陶瓷材料间的粘结力就越大。因此,本文通过计算粘结剂与HA(110)界面间的结合能来评价三种粘结剂在生物陶瓷表面的粘结特性。其表达式如下,
Ebind=-Einter=-(Etotal-Epolymer-EHA)
(4)
式中Etotal,Epolymer和EHA(110)分别为高聚物与HA相互作用体系、高聚物和HA(110)的能量。通过对PVP/HA(110)和PAM/HA(110)和PVA/HA(110)的相互作用平衡体系进行MD模拟计算,得到的结合能列入表3。
由表3可知,三种粘结剂与HA(110)的结合能大小关系是PAM>PVA>PVP。这表明相比PVA和PVP两种粘结剂,PAM与HA(110)表面的粘结作用力更强,这与三种粘结剂的内聚能大小关系是一致的。产生这种现象的主要原因是,在相同质量的三种粘结剂中含有不同数量和类型的极性官能团。其中,一条PVP分子链含有20个羰基(-C=O),PVA分子链中含有50个羟基(-OH),但是在PAM分子链中却含有31个羰基(-C=O)和31个氨基(-NH2)。因此,在三种粘结剂中,PAM的极性是最强的,这也是PAM/HA(110)界面结合能最大的根本原因所在,同时也说明高分子粘结剂的化学结构和官能团是影响粘结剂粘结性能的关键所在。
表3 三种相互作用模型的结合能(单位:kJ/mol)
Tab.3 Binding energies of three interaction models(unit:kJ/mol)

SystemEtotalEploymerEHAEbindPVP/HA(110)39806733.5736773.0339917760.62147800.08PAM/HA(110)39706546.8958660.4639917652.18269765.65PVA/HA(110)39744011.1349372.8839917777.98223139.73

图5 三种粘结剂与HA(110)相互作用模型
Fig.5 Interaction models of three binders on HA(110) interface
4 结 论
本文借助分子动力学方法,对骨支架粉末粘结工艺中三种常用聚合物粘结剂PVP,PAM和PVA进行建模,并且对其平衡结构进行了计算分析,得到了三种粘结剂的基本性质。结果表明,粘结剂的内聚能大小关系为PAM>PVA>PVP,这与粘结剂体系的密度大小关系一致。静态力学分析结果表明,三种粘结剂体系的机械强度大小关系为PVA>PVP>PAM,其与体系内聚能和密度的大小关系并不一致,说明内聚能与力学性能之间并不存在特定的关系。此外,界面结合能的计算结果表明,三种粘结剂与HA 的结合能大小关系是PAM>PVA>PVP,与粘结剂内聚能的大关系一致,产生这一现象的根本原因是相同质量高分子粘结剂中所含官能团的数量和类型不一样。因此,高分子粘结剂的化学结构和官能团是影响粘结剂粘结性能的关键所在。
:
[1] Chiu C,Ferreira J,Luo T J,et al.Direct scaffolding of biomimetic hydroxyapatite -gelatin nanocomposites using aminosilane cross-linker for bone regeneration [J].JournalofMaterialsScience-MaterialsinMe-dicine,2012,23(9):2115-2126.
[2] Wang Y E,Li X P,Wei Q H,et al.Study on the mechanical properties of three -dimensional directly binding hydroxyapatite powder [J].CellBiochemBiophys,2015,72(1):289-295.
[3] Bergmann C,Lindner M,Zhang W,et al.3D printing of bone substitute implants using calcium phosphate and bioactive glasses [J].JournaloftheEuropeanCeramicSociety,2010,30(12):2563-2567.
[4] Vorndran E,Klarner M,Klammert U,et al.3D powder printing of b-tricalcium phosphate ceramics using different strategies [J].AdvancedEngineeringMaterials,2008,10:B67-B71.
[5] Wei Q H,Wang Y N,Li X P,et al.Study the bonding mechanism of binders on hydroxyapatite surface and mechanical properties for 3DP fabrication bone scaffolds [J].JournaloftheMechanicalBehaviorofBiomedicalMaterters,2016,57:190-200.
[6] Wang Y N,Wei Q H,Pan F L,et al.Molecular dynamics simulations of the mechanical properties of HA/NBCA under Additive Manufacturing[J].BiomedicalMaterialsandEngineering,2014,24:825-833.
[7] 干 湧,江 山,苏昱臻,等.基于分子动力学与耗散粒子动力学串行耦合的面心立方金属粗粒化模型[J].计算力学学报,2016,33(4):621-628.(GAN Yong,JIANG Shan,SU Yu-zhen.A coarse -grained model for fcc metals based on hierarchical coupling between molecular dynamics and isothermal dissipative particle dynamics [J].ChineseJournalofComputationalMechanics,2016,33(4):621-628.(in Chinese))
[8] 田 霞,崔俊芝.基于分子动力学模拟的多晶结构微观热-力耦合行为的计算[J].计算力学学报,2012,29(1):95-98.(TIAN Xia,CUI Jun-zhi.Computations of the thermo -mechanical behaviors of polycrystalline structures at micro -scale based on molecular dynamics [J].ChineseJournalofComputationalMecha-nics,2012,29(1):95-98.(in Chinese))
[9] Zhang H P,Lu X,Leng Y,et al.Molecular dynamics simulations on the interaction between polymers and hydroxyapatite with and without coupling agents[J].ActaBiomaterialia,2009,5:1169-1181.
[10] 潘海华,陶锦辉,吴 韬,等.羟基磷灰石界面水行为的分子模拟 [J].无机化学学报,2006,22(8):1392-1400.(PAN Hai-hua,TAO Jing-hui,WU Tao,et al.Molecular simulation of water behavior on Hydroxya-patite crystal faces [J].ChineseJournalofInorganicChemistry,2006,22(8):1392-1400.(in Chinese))
[11] 李 敏.骨组织工程用多孔羟基磷灰石及其复合材料的制备与性能[M].湖南:湖南科技大学,2008.(LI Min.PreparationandPropertiesofHydroxyapatiteandItsCompositesinBoneTissueEngineering[M].Hunan:University of Science and Technology of Hunan,2008.(in Chinese))
[12] Wei Q H,Wang Y E,Chai W H,et al.Effects of composition ratio on the properties of poly (vinyl alco -hol)/poly (acrylic acid) blend membrane:a molecular dynamics simulation study [J].MaterialsandDesign,2016,89:848-855.
[13] Sun H.COMPASS:an ab initio force -field optimized for condensed-phase application overview with details on alkane and benzene compounds [J].TheJournalofPhysicalChemistryB,1998,102(38):7338-7364.
[14] Andersen H C.Molecular dynamics simulations at constant pressure and/or temperature [J].JournalofChemicalPhysics,1980,72(4):2374-2383.
[15] Tosi M P.Cohesion of ionic solids in the Born model [J].SolidStatePhysics,1964,16:1-120.
[16] Ewald P P.Evaluation of optical and electrostatic lattice potentials [J].AnnalsofPhysic,1921,369(3):253-287.
[17] Dong S J,Yan J T,Xu N,et al.Molecular dynamics simulation on surface modification of carbon black with polyvinyl alcohol [J].SurfaceScience,2011,605(9-10):868-874.
[18] Swenson R J.Comments on virial theorems for bounded systems [J].AmericanJournalofPhysics,1983,51(10):940-942.
[19] 魏庆华,汪焰恩,杨明明,等.HA/PLA复合材料界面相互作用及其力学性能的MD模拟[J].功能材料,2013,44(21):3089-3093.(WEI Qing-hua,WANG Yan-en,YANG Ming-ming,et al.Molecular dynamics simulation of mechanical properties and surface inte -raction for HA/PLA [J].ChineseFunctionalMaterials,2013,44(21):3089-3093.(in Chinese))
