基于改进粒子群的薄壁变截面刚架临界载荷优化算法

， ， ，

(1.沈阳建筑大学 机械工程学院，沈阳 110168；2.沈阳建筑大学 土木工程学院，沈阳 110168)

1 引 言

大型薄壁刚架稳定性一直是工程结构中的重点研究问题[1]。与等截面刚架相比，变截面刚架因其具有充分利用材料强度、节约经济、受力合理以及更好适应截面应力变化的优点而在实际工程中广泛应用[2]。由于截面变化将导致刚度改变，因此在研究变截面刚架稳定性时通常无法获取相应的临界载荷解析表达式。

目前工程中普遍运用的是取等效截面计算的有效宽度法求解变截面刚架临界载荷[3]。非线性数值求解方法已逐渐成为变截面问题的研究重点。郭彦林等[4]运用非线性屈曲分析考察了房顶表面均布荷载对刚架柱稳定性的影响，重申了数值求解在变截面研究中的实用性。Ermopoulos[5]在前人研究的基础上，通过设置不同的约束条件限制自由度，分析了楔形变截面杆在不同条件下的受力情况，从而得到相应的特征方程。王欣等[6]为了探究压杆稳定性，建立n阶变截面压杆的非线性微分方程组，以建立适应边界条件的状态方程组，求解获取递推关系式，从而应用Newton法迭代计算临界载荷。在非线性方程组优化方面，群智能算法由于其具备较快的收敛速度、高鲁棒性和较强的局部及全局搜索能力而在近些年受到广泛推崇[7]。肖志权等[8]采用遗传算法，以机械臂的结构以及传感器和控制器的参数为设计变量，建立无约束优化，从而减小了变截面梁的末端振动。武和全等[9]基于神经网络，结合遗传算法建立了变截面梁结构的总吸能神经网络预测模型，从而改善了汽车车架变截面薄壁梁结构尺寸，提高了安全性。朱剑宝等[10]通过运用标准粒子群算法优化变截面板簧，以弹簧质量最小为目标函数，从而有效降低板簧余重1/3以上。在变截面稳定性研究方面，侯祥林等[11]基于数值优化思想提出了超静定压杆结构临界载荷的数值迭代算法和基于传统无约束的优化算法，有效提高了临界载荷计算精度。

针对工程中广泛运用的变截面刚架，在非线性小变形前提下，通过刚架拆分和节点设置，运用差分法构造以节点位移和临界偏载等为未知变量的非线性方程组，提出基于粒子优胜劣汰的改进粒子群算法[12]IPSO(Improved Particle Swarm Optimization)进行无约束优化求解，进而得出刚架临界荷载及其变形图。在此基础上，针对变截面桥式起重机的工程算例，探讨柱脚为固定端的超静定刚架在受非对称偏载时的稳定性问题，并运用ABAQUS进行有限元仿真对比。通过算法的提出与实现为实际工程设计和分析提供支持。

2 刚架临界载荷求解问题分析

图1所示为一类典型对称结构非对称载荷刚架结构示意图。图中单跨单层刚架柱脚刚接，边柱AB与CD长度分别为l1和l4，弯曲刚度分别为EI(x1)和EI(x4)；横梁BC长l2，弯曲刚度为EI(x2)。弯曲刚度随着坐标x而变化。Fc r为施加于刚架上的临界单一偏载，由于结构对称，左右立柱皆可施加。基于小变形线弹性稳定性理论，临界偏载作用下，刚架将远在材料屈服前产生微小扰动偏离，但尚未失稳，处于可恢复的临界平衡状态。设未知的挠曲轴线方程y=f(x)，考虑构造求解解析解难以获得的非线性差分方程组[13]。

刚架受非对称载荷，导致变形不能简单依靠对称计算，所以通过拆分刚架，将变形刚架分成边柱AB段、边柱CD段、横梁BK段和横梁KC段四个部分。其中未知点K为横梁变形后挠度为0的点，且BK长度为l2,KC长度为l3，对应分别建立xj-wj(j=1,2,3,4)四个直角坐标系。将各部分沿x坐标轴离散成ni段，取Δxi=li/ni(i=1,2,3,4)。w为挠度值，对应挠度坐标为wi(i=0,1,2,…,ni)，挠曲轴线离散点坐标为(xi,wi)(i=0,1,2,…,ni)。刚架拆分稳定性分析如图2所示。

建立各部分挠曲线微分方程：

EI(x)w″=M(x)

(1)

图1 刚架受偏载荷结构示意图

Fig.1 Structural diagram of the bias load pressed frame

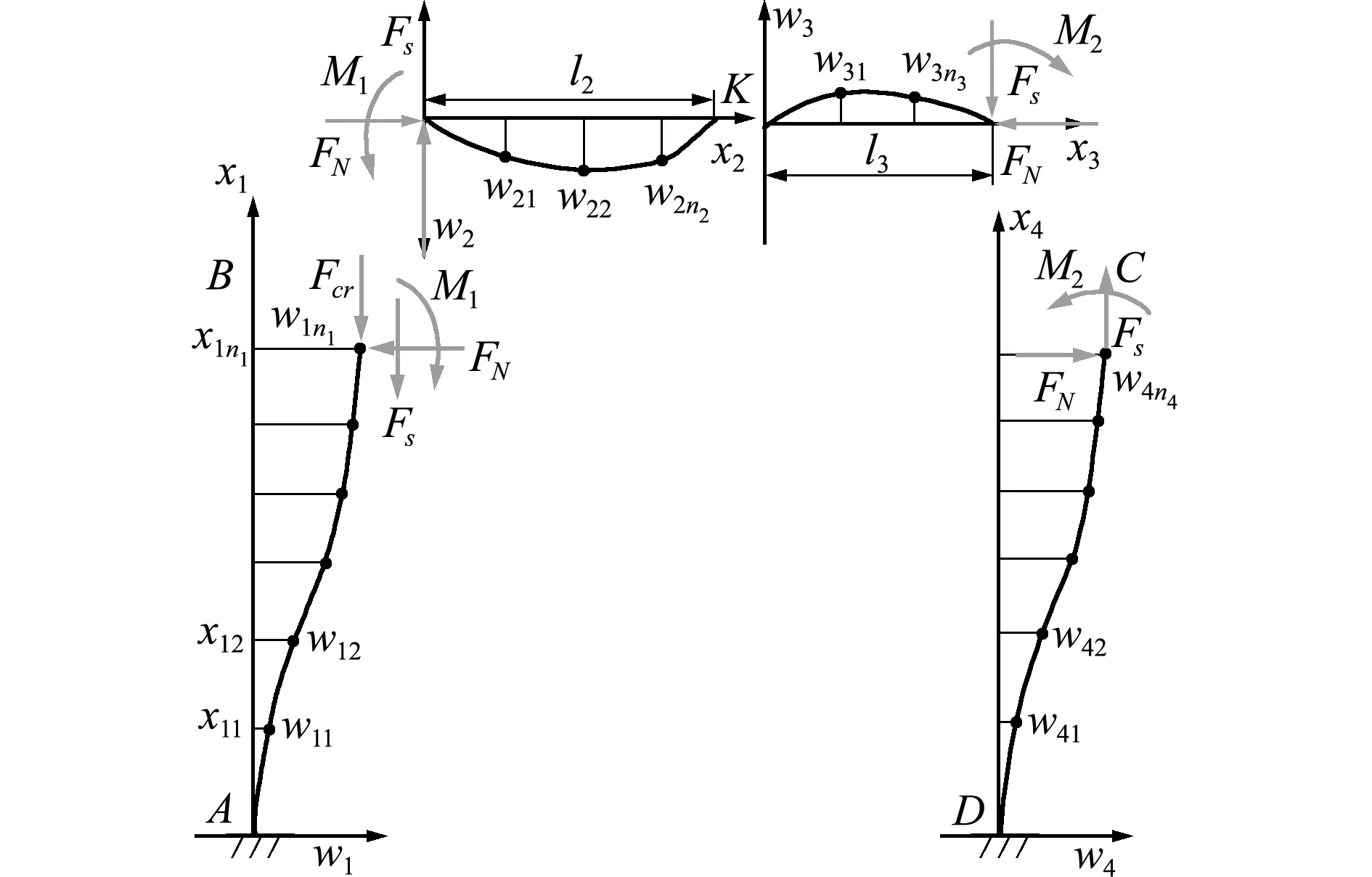
图2 刚架拆分示意图

Fig.2 Schematic diagram of disconnected frame

对于AB段，设柱段节点数量为n1，则

M(x1)=M1-FN(l1-x1)+Fc r(w1n1-w1)+

Fs(w1n1-w1)

(2)

将式(2)代入式(1)得

Fs(w1n1-w1)

(3)

对BK段、KC段和CD段分别设柱段节点数量为n2，n3和n4，则

(4)

(5)

(6)

(EI1(x1)/EI20)(w1(i +1)-2w1i+w1(i -1))=

(7)

(EI2(x2)/EI20)(w2(i +1)-2w2i+w2(i -1))=

(8)

(EI3(x3)/EI20)(w3(i +1)-2w3 i+w3(i -1))=

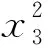
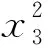
(9)

(EI4(x4)/EI20)(w4(i +1)-2w4i+w4(i -1))=

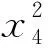
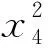
(10)

式中EIj 0=EIj(0)(j=1,2,3,4)；i=1,2,…,n-1。

(11)

如图1所示，柱脚A和D处为固定端约束，可通过增加补点即w1(-1)=w11和w4(-1)=w41得

2w11c1(x10)-m1+fnl1-fc rw1n1-fsw1n1=0

(12)

2w41c4(x40)+m2-fnl4+fsw4n4=0

(13)

式中x10和x40分别为x1和x4坐标轴上的第0点。

微分方程组中共有n1+n2+n3+n4-4个非线性差分方程。其中有wj i(i=1,2,…,nj-1,j=1,2,3,4)、柱顶点挠度w1n1和w4n4、柱端剪力Fs、柱端弯矩M1和M2、轴力FN、临界偏载荷Fc r以及BK段长度l2，总共n1+n2+n3+n4+4个未知量。

针对刚架各部分边界条件为

由柱脚刚接可知柱脚A和D无挠度无转角

(14)

(15)

由横梁BC弯矩平衡，则

m1-fsl2-m2=0

(16)

为了保证柱梁连续，即保证柱梁接点弯矩和转角相同，则转角等式为

(17，18)

在临界偏载Fc r作用下，挠曲线的各节点挠度值将构成一定的比例关系，即形成一组相对的模态解，为了方便求解及程序运算，取柱AB段任意节点P的挠度值为w1P，则可增加方程

w1P=c

(19)

式中c为任意正常数。

基于小变形稳定理论，刚架柱AB段及柱CD段可视为相同变形条件，即设

w1n1=w4n4

(20)

为了寻求BK段长度l2，因为K点挠度为0，构建横梁为静定结构，运用图乘法计算挠度，则得K点挠度方程为

(21)

通过补充方程(14～21)，方程组总个数变为n1+n2+n3+n4+4，方程数等于未知量个数，理论上挠曲线可唯一确定。

针对变截面问题形成的非线性差分方程组不能运用解析法求解，因此构造临界荷载的优化求解算法。

3 IPSO临界载荷优化算法求解原理

标准粒子群算法(PSO)是Shi等[14]在前人研究基础上引入惯性权重ω后得到的。通过惯性权重ω，粒子将具有更好的收敛性且不易飞跃边界导致发散，从而保证算法局部搜索与全局搜索能力的平衡。为了提高算法搜索效率，Shi等[15]提出通过线性递减惯性权重LDIW(Linear Decreasing Inertia Weight)。针对本文的多维算例，采用线性递减惯性权重粒子群算法作为算法改进模板。惯性权重计算公式为

ω(k)=ωend+(ωstart-ωend)[(K-k)/K]

(22)

式中k=1,2,…,K为当前迭代次数，K为设定最大迭代次数，ωstart为初始惯性权重，ωend为迭代满次时的惯性权重。

通过实验仿真，线性递减惯性权重粒子群算法虽然相比标准粒子群算法在搜索速度和精度上得到很大提高，但仍然具有多数群体智能算法早期收敛速度快但后期收敛精度不够或陷入局部最优的缺点。通过研究早熟粒子，发现粒子受随机起点位置影响，导致在惯性权重下降的搜索后期速度下降，使得越来越多的粒子无法趋近最优解或成为无用僵化的早熟粒子。

针对上述现象，提出一种基于适应度评估适者生存的粒子更新粒子群算法。具体步骤如下。

(1) 初始化。在D维的搜索空间内，设计种群粒子数为n，记{Xi}={X1,X2,…,Xn}，每个元素视为一个D维解集且为粒子位置，即初始化粒子i的位置和速度为

Xi=(xi 1,xi 2,…,xi D)T(i=1,2,…,n)

(23)

Vi=(vi 1,vi 2,…,vi D)T(i=1,2,…,n)

(24)

(2) 适应度评估。通过需要求解的适应度函数function()评选种群最佳粒子位置gbest和第i个粒子的历史粒子位置pbest[i]。

(3) 更新粒子位置。运用粒子群位置和速度更新公式获取新的粒子第d维(1≤d≤N)位置和速度，即[16]

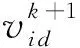
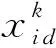
(25)

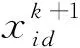
(26)

式中c1为局部惯性权重因子，c2为全局惯性权重因子,rand()为(0,1)间的随机数,k=1,2,…,K为迭代次数。

(4) 适者生存。每隔Z轮再次计算n个粒子的适应度，依据适者生存淘汰机制，随机淘汰P个粒子，P取[n/2α,n/α]间的随机整数[17]，α为更新系数。并补充P个粒子，其第d维(1≤d≤N)位置和速度为

vj d=rand(vmin,vmax)

(j=1,2,…,P) (27)

xj d=rand(xmin,xmax)

(j=1,2,…,P) (28)

式中vmin和vmax为群体淘汰P个粒子后第d维的最小速度和最大速度,xmin和xmax为群体淘汰P个粒子后第d维位置的最小值和最大值。

(5) 停止条件。循环回到步骤(2)，直至达到设定的最大迭代数K或设定精度ε。优化程序流程如图3所示。

对称结构变截面刚架临界载荷最优化问题：

min.f(z)

(29)

式中z∈RN为动态设计变量，N=n1+n2+n3+n4+4为动态设计变量z的维数。设置：

zi=w1i(i=1,2,…,n1)

zi + n1=w2i(i=1,2,…,n2-1)

zi + n1+ n2=w3i(i=1,2,…,n3-1)

zi + n1+ n2+ n3=w4i(i=1,2,…,n4)

zN -5=m1,zN -4=m2,zN -3=fn,zN -2=fs

zN -1=fc r,zN=l2,l=l2+l3

构建目标函数f(z)为

m1+fn(l1-x1)-fc r(w1n1-w1i)-

2w2i+w2(i -1))+m1-fnw2i-fsx2]2+

2w4i+w4(i -1))+m2-fn(l4-x4)+

fs(w4n4-w4i)]2+(w1P-c)2+

[2w11c1(x10)-m1+fnl1-fc rw1n1-fsw1n1]2+

[2w41c4(x40)+m2-fnl4+fsw4n4]2+

(w1n1-w4n4)2+[m1-fsl-m2]2+

(30)

通过最优化求解，所求优化函数的极小值f(z*)→0,从而输出满足精度的N维z=z*解集[18]。算法基于eclipse 开发平台用JAVA语言编写。

4 工程算例

本文选用常见构型相对简单的变截面桥式起重机为工程算例，对优化算法和程序进行考证。几何尺寸如图4(a)所示。其中横梁为等截面梁跨度l=34 m，其截面尺寸如图4(b)所示，截面高度h1=2000 mm，截面宽度b1=1600 mm。起升高度即边柱为变截面高度，为l1=l4=16.5 m，其截面尺寸如图4(c)所示，大头截面高度h2=3200 mm，截面宽度b2=1026 mm，小头截面高度h3=2600 mm，横梁边柱皆为箱型结构。边柱与主梁和下横梁均为刚性连接，下横梁与地面接触为起重机提供支撑，其对起重机的整体稳定性影响可以忽略。不考虑起重机下横梁对整体稳定性的影响，认为两柱腿与地面采用固定约束。取截面厚度t=12 mm，起重机左端受未知偏载荷如图1所示，通过优化算法求解未知偏载荷，即临界载荷Fc r及刚架变形。

图3 优化程序流程

Fig.3 Optimization program flowchart

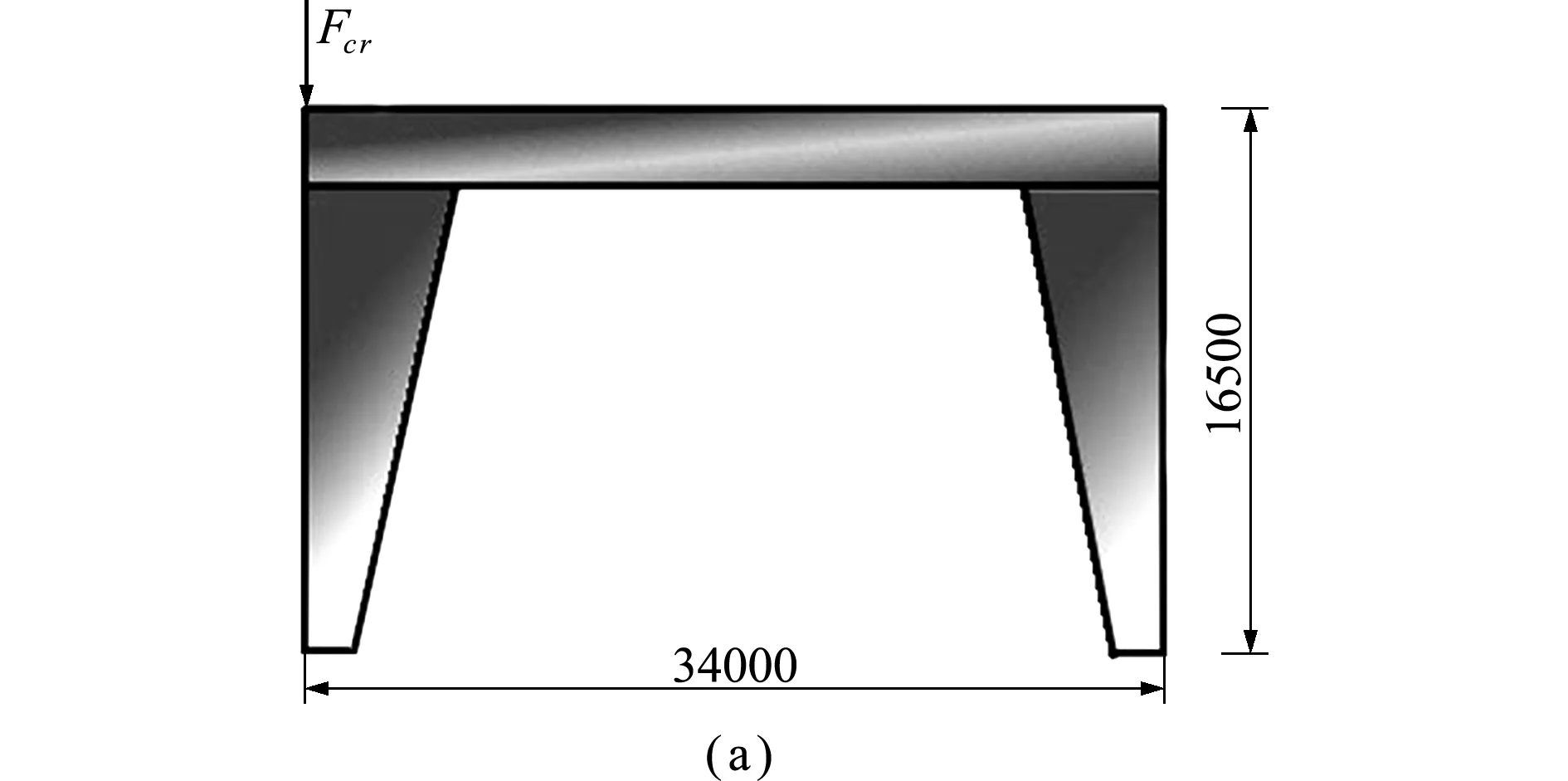
图4 变截面刚架算例力学模型

Fig.4 Variable cross-section compression frame mechanical modes of example

求解变截面稳定性问题，由于截面惯性矩随着截面尺寸的变化而变化，因此弯曲刚度也时刻变化，关系式为

(31)

h(x)=h3+(h2-h3)/l1

(32)

(33)

取段数n1=n2=n3=n4=11，设计变量数N=48，z1～z42为挠度对应wi j(i=1,2,3,4；j=1,2,…,11)，z43为简化弯矩m1，z44为简化弯矩m2，z45为简化轴力fn，z46为简化剪力fs，z47为简化临界载荷fc r，z48为BK段长l2。IPSO搜索精度ε=10-7，设计粒子总数为40，初始迭代次数K=40000，取粒子速度初值为Vi=rand()(i=1,2,…48)，位置初值为Xi=rand()(i=1,2,…，48)。通过38571次优化计算达到预定精度。力与弯矩的各简化变量优化过程列入表1。

因此，对应的简化形式临界载荷为

fc r=0.0592

则临界载荷为

Fc r= 0.0592×EI20=

0.0592×2.06×1011I20=

(1.6-0.024)×(2-0.024)3]=

6.512×105kN

满足精度后的刚架的42个离散节点挠度与5个无量纲参数列入表2。依据表2各点挠度绘制变截面刚架在临界偏载情况下的位型，如图5所示。

表1 优化计算过程表Tab.1 Optimized calculation process

表2N=48个设计变量优化计算结果

Tab.2 Optimization results of design variables

(N=48)

动态变量优化结果动态变量优化结果动态变量优化结果z10.0112z170.3977z330.0202z20.0414z180.3262z340.0498z30.0880z190.2408z350.0952z40.1496z200.1515z360.1584z50.2254z210.0679z370.2411z60.3152z220.1238z380.3451z70.4192z230.2324z390.4717z80.5384z240.3225z400.6222z90.6738z250.3909z410.7979z100.8270z260.4344z421.0000z111.0000z270.4497z43-0.0234z120.2112z280.4339z440.0288z130.3524z290.3840z450.0013z140.4325z300.2969z46-0.0015z150.4604z310.1698z470.0592z160.4457z320.0044z4820.1462

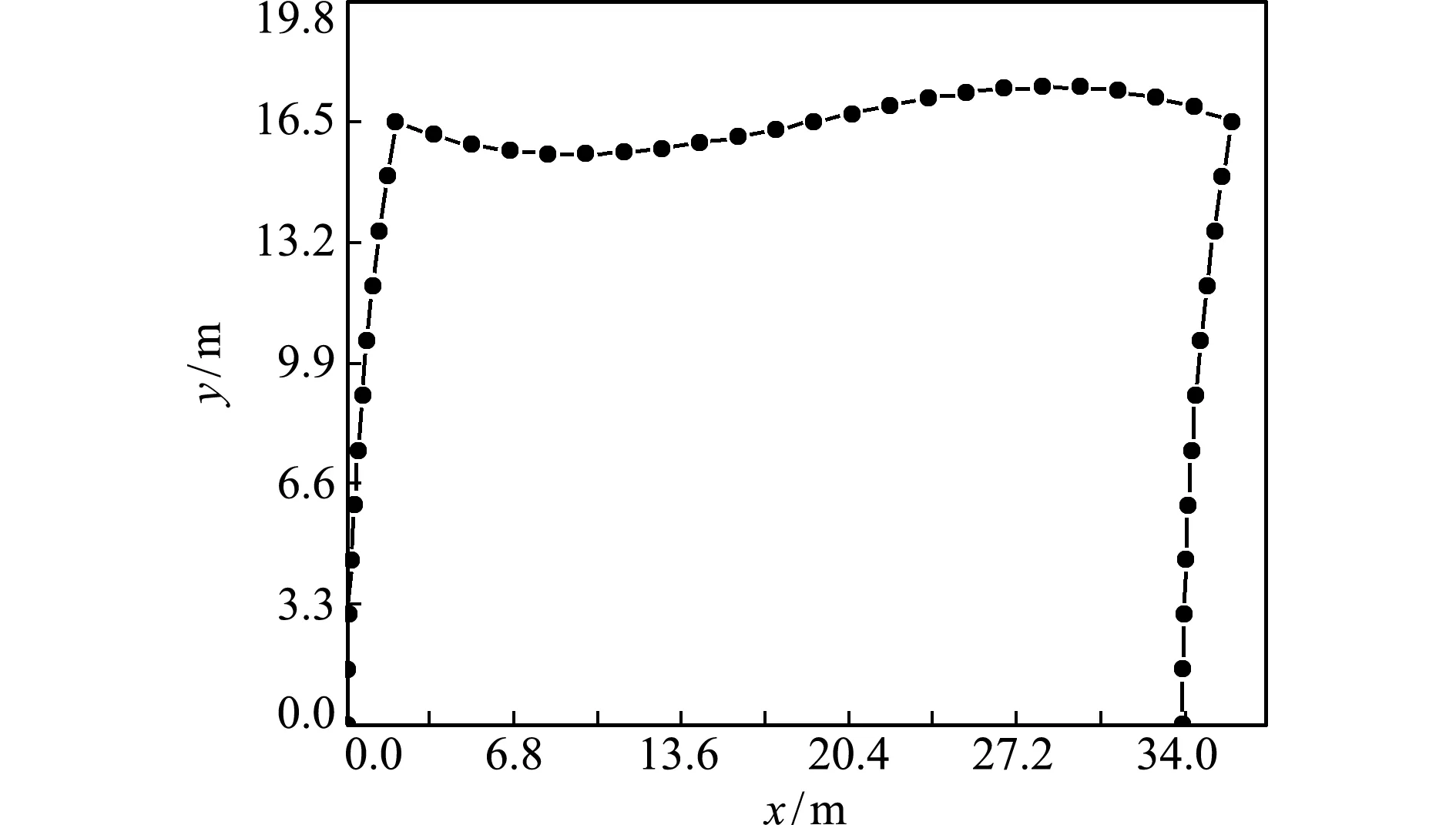
图5 变截面刚架在临界载荷作用下的位型

Fig.5 Variable cross-section compression frame deformation

运用ABAQUS有限元仿真软件，设置钢材弹性模量E=2.06×105N/mm2，泊松比μ=0.3，单元类型为B31，模型节点数为2143，单元数为714。

仿真计算临界载荷结果为

Fc r,s=6.0505×105kN

则本文算法与ABAQUS计算的相对误差为

ε′=7.63%

因此本文算法与仿真结果十分接近。

ABAQUS仿真变形图如图6所示。

图6 变截面刚架在ABAQUS下的屈曲模型

Fig.6 Variable cross-section compression frame buckling model through ABAQUS

5 结 论

本文针对小变形下变截面对称刚架受非对称载荷的实际工况，分析计算了刚架梁柱弹性变形形变及临界载荷等参数。主要结论如下。

(1) 所述临界载荷算法，基于差分思想和优化原理，运用改进粒子群算法嵌套工程实例，编程计算了变截面刚架的临界载荷算例。

(2) 通过ABAQUS仿真对比，本文算法具有足够精准性，相比常规的有效宽度法能更好地描述刚架受力下位型和载荷的力学关系，进一步为工程设计与分析提供支持。

:

[1] 龙驭球,包世华.结构力学(第二版)[M].北京:高等教育出版社,1996.(LONG Yu-qiu,Bao Shi-hua.StructuralMechanics(2n dEdition)[M].Beijing：Higher Education Press，1996.(in Chinese))

[2] 单辉祖.材料力学I(第3版)[M].北京：高等教育出版社，2009.(SHAN Hui-zu.MaterialMechanics(3r dEdition)[M].Beijing：Higher Education Press，2009.(in Chinese))

[3] GB51022-2015.门式刚架轻型房屋钢结构技术规范[S].北京:中国建筑工业出版社，2015.(GB51022-2015.Technical Code for Steel Structure of Light-Weight Building with Gabled Frames [S].Beijing:China Building Industry Press,2015(in Chinese))

[4] 郭彦林,王文明,石永久.变截面门式刚架结构的非线性性能[J].工程力学,2000,17(4):29-36.(GUO Yan-lin,WANG Wen-ming,SHI Yong-jiu.Nonlinear behavior of portal frame with tapered members [J].EngineeringMechanics,2000,17(4):29-36.(in Chinese))

[5] Ermopoulos J C.Buckling of tapered bars under stepped aaial loads[J].JournalofStructuralEngineering,1986,112(6):1346-1354.

[6] 王 欣,易怀军,赵日鑫,等.一种n阶变截面压杆稳定性计算方法的研究[J].中国机械工程，2014,25(13)：1744-1747,1799.(WANG Xin,YI Huai-jun,ZHAO Ri-xin,et al.Research on stability analysis method ofn-order variable cross-section compressed bars[J].ChinaMechanicalEngineering，2014,25(13)：1744-1747,1799.(in Chinese))

[7] 张碧玲,胡凌霄,刘 勇,等.采用改进粒子群算法的微电网短期调控模型[J].电网技术，2016,40(6)：1717-1723.(ZHANG Bi-ling,HU Ling-xiao,LIU Yong,et al.Short-term scheduling model for micro-grids with improved discrete particle swarm optimization[J].PowerSystemTechnology，2016,40(6)：1717-1723.(in Chinese))

[8] 肖志权,崔玲丽.基于遗传算法的柔性机械臂的同时优化设计[J].机器人,2004,26(2):170-175.(XIAO Zhi-quan,CUI Ling-li.GA based concurrent optimization and design of flexible manipulator system[J].Robot，2004,26(2):170-175.(in Chinese))

[9] 武和全,辛 勇.基于神经网络的变截面梁抗撞性分析及优化设计[J].振动与冲击,2010,29(10):102-107,174.(WU He -quan,XIN Yong.Crashworthiness optimization of a thin-walled rail with variable section based on artificial neural network[J].JournalofVibrationandShock，2010，29(10):102-107,174.(in Chinese))

[10] 朱剑宝,张卫波.基于PSO算法和ANSYS的变截面板簧优化仿真设计[J].福建工程学院学报,2008,6(s1):74-78.(ZHU Jian-bao,ZHANG Wei-bo.Optimized simulation design of taper leaf spring based on particle swarm optimization algorithms and ANSYS[J].JournalofFujianUniversityofTechnology,2008,6(s1):74-78.(in Chinese))

[11] 侯祥林,王似巍,王家祥,等.一类超静定变截面压杆临界荷载的优化算法[J].沈阳建筑大学学报(自然科学版)，2017,33(1):104-110.(HOU Xiang-lin,WANG Si-wei，WANG Jia-xiang，et al.An optimization algorithm for the critical load of a class of statically indeterminate variable cross-section compression bar[J].JournalofShenyangJianzhuUniversity(NaturalScience)，2017,33(1):104-110.(in Chinese))

[12] Kennedy J,Eberhart R.Particle swarm optimi-zation[A].International Conference on Neural Networks[C].1995.

[13] 侯祥林,刘铁林,翟中海.非线性偏微分方程边值问题的优化算法研究与应用[J].物理学报,2011,60(9)：090202.(HOU Xiang-lin,LIU Tie -lin,ZHAI Zhong-hai.Study and application of optimization algorithm about nonlinear partial differential equations with boundary value problem[J].ActaPhysicaSinica，2011,60(9)：090202.(in Chinese))

[14] Shi Y，Eberhart R.A modified particle swarm optimizer[A].World Congress on Computational Intelligence[C].Anchorage,AK,USA,1998.

[15] Shi Y，Eberhart R C.Empirical study of particle swarm optimization[A].Congress on Evolutionary Computation[C].Washington,DC,USA，1999.

[16] 周福家,张宏伟,李卫国.分子网络多靶标筛选的粒子群数值模拟法[J].计算力学学报，2015，32(2)：269-273,279.(ZHOU Fu-jia，ZHANG Hong-wei,LI Wei-guo.Multiple target optimal intervention using particle swarm optimization in molecular network[J].ChineseJournalofComputationalMechanics,2015，32(2)：269-273,279.(in Chinese))

[17] Wu H S，Zhang F M.Wolf pack algorithm for unconstrained global optimization[J].MathematicalProblemsinEngineering，2014，31(1)：1-17.

[18] 侯祥林,胡建强,卢宏峰,等.变截面压杆稳定非线性微分方程边值问题的最优化算法研究[J].计算力学学报，2017,34(2):137-142.(HOU Xiang-lin，HU Jian-qiang，LU Hong-feng，et al.Optimization algorithm of boundary value problem of stable nonlinear differential equation for variable cross-section compression bar[J].ChineseJournalofComputationalMechanics,2017,34(2)：137-142.(in Chinese))