接触-碰撞算法研究进展

, ,

(1.中国工程物理研究院总体工程研究所，绵阳 621900;2.北京理工大学 前沿交叉科学研究院，北京 10081；3.北京理工大学 爆炸科学与技术国家重点实验室，北京 10081)

1 引 言

变形体间的接触-碰撞(或称为动态接触)广泛存在于实际工程中[1-4]，如弹体穿甲/侵彻、安全防护、汽车防撞以及冲压成形等。该类问题通常涉及几何、材料与边界的三重非线性，属于最困难的非线性问题之一[3,4]，数值方法是解决此类问题的最有效手段。大量分析表明[5]，接触-碰撞算法是影响数值计算精度的重要因素。另一方面，接触-碰撞过程中接触界面与接触状态的确定非常耗时，接触计算通常占到问题总求解时间的一半以上[6,7,8]。因此，发展高效、高精度的接触-碰撞算法对于实际工程应用非常迫切。

接触-碰撞数值算法的研究大致起始于20世纪70年代，迄今已有很多学者开展了相关研究，发展了许多优秀算法。Bourago等[9]较全面地列出了拉格朗日、非拉格朗日网格及无网格方法相关接触界面算法的635篇论文和专著，钟阳等[10]总结了显式有限元计算常用的接触界面搜索算法与接触约束算法。然而，由于接触-碰撞问题的复杂性，如接触界面不光滑、接触对动态变化等，现有算法在健壮性、精度及效率等方面仍需发展和完善。目前尚没有一种算法可准确高效地处理所有接触-碰撞问题，接触-碰撞模拟仍是一个具有挑战性的问题。

基于拉格朗日框架的显式有限元是处理变形体间接触-碰撞最常用的数值方法，因此本文主要针对显式拉格朗日有限元相关的接触-碰撞算法进行总结分析。

2 接触界面的离散

变形体间接触-碰撞问题的有限元理论与基本数值方法可参考文献[1-4]。本文仅概要给出该类问题的力学描述、有限元求解模型与基本列式。

接触-碰撞算法可处理任意多个物体间的相互作用，多物体间的接触可归结为物体间的两两作用。不失一般性地，本文以两个物体间的接触为例给出其数学描述。如图1所示，相互接触的两个变形体A和B，t时刻的构形分别标识为ΩA和ΩB，其边界分别为ΓA和ΓB，边界的外法向分别为nA和nB，接触边界为ΓC。

接触-碰撞系统除应满足通常的连续体控制方程外以及接触界面上还应满足一定的运动学条件与动力学条件[4]：不可侵入条件和动量守恒。考察位于接触界面上分别隶属于物体A与物体B的任意两个点xA和xB，不可侵入条件可表述为

图1 两个物体间的接触

Fig.1 A two -body contact system

gN=(xB-xA)·nA≥0

(1)

即两物体间的间隙要求大于或等于0，0值对应于接触状态，gN称为间隙函数(其负值称为侵入深度)。界面的动量守恒要求作用于两物体的面力tA与tB满足

tA+tB=0

(2)

如果不考虑接触面的焊接或粘接作用，界面法向作用力pN只能为压力，即

pN≡tA·nA≤0

(3)

与不含接触的问题相比，接触-碰撞系统仅需在接触界面上额外引入约束条件(1～3)。因此，可方便地建立接触-碰撞系统的控制方程弱形式[11](本文暂不考虑界面间的摩擦)：

(4)

(5)

对应于接触界面约束的罚函数法弱形式。若pN考虑为独立变量，则

(6)

即为拉格朗日乘子法的弱形式。

对方程(4)进行有限元离散，可得半离散方程：

Man=fextn-fintn+fcn

(7)

式中M为质量矩阵，an为加速向量，fextn和fintn分别为节点外力向量与节点内力向量，fcn为节点接触力向量，下标n标识时间迭代步。

中心差分法是显式有限元最常用的积分方法，此时方程(7)的时域离散可概括为

an=M-1(fextn-fintn+fcn)

(8)

vn + 1 / 2=vn - 1 / 2+anΔtn

(9)

un +1=un+vn + 1 / 2Δtn + 1 / 2

(10)

式中 Δtn + 1 / 2=tn + 1-tn，Δtn=tn + 1 / 2-tn - 1 / 2；vn + 1 / 2和vn - 1 / 2分别为tn + 1 / 2和tn - 1 / 2时刻的速度；un和un + 1 / 2为相应时刻的节点位移向量。

采用显式积分求解时，方程(8)右端项中唯一的未知量为tn时刻的节点接触力向量fcn；接触-碰撞算法研究的目的就是发展健壮、精确和高效的方法以求得fcn。

接触-碰撞问题中，接触面通常不能事前确定，并且随时间动态变化，因此接触力计算可进一步分解为接触搜索与接触约束施加两个子问题。接触搜索的目的是确定系统中哪些部位发生了接触或者哪些原已接触的部位发生了分离或滑移，接触约束施加则根据系统当前接触状态计算出界面接触力以满足接触约束条件。

有限元方法中，相互接触的变形体(接触体)离散为有限单元，接触界面即为变形体外表面的单元面集合或节点集合。这样，接触体间的作用转化为离散的节点间、节点与单元面或单元面间的相互作用。

为便于问题描述，本文采用Hallquist等[12,13]提出的主从概念。相互接触的两个物体，一个为主控体，一个为从属体。隶属于主控体的接触界面称为主面，构成主面的单元外表面称为主片，相应的节点称为主点。类似地，定义从属体上的接触实体为从面、从片和从点。

根据接触界面离散方式的不同，界面模型可分为三类。

(1) 点-点NTN(node -to -node)模型[14]。接触界面上从点与主点一一对应，接触过程中从点与主点几何位置保持一致。这种离散模型的局限是仅适用于小变形且不存在界面相对滑动的接触分析，如线性准静态问题；主面与从面的网格划分需要保证主点与从点几何位置一一对应。由于适应性差且误差偏大，即使对于小变形问题分析，目前也已很少采用这种模型。

(2) 点-面NTS(node -to -segment)模型[11-13]。该类模型将两物体间的接触离散为从点与主片间的相互作用，通过强制从点不能侵入主片来施加接触约束条件。该模型对接触界面网格离散几乎没有限制，并且可应用于接触界面任意滑移等复杂问题，是目前最常用的界面离散方式。

(3) 面-面STS(segment-to -segment)模型[15,16]。面-面接触是近年发展起来的一种计算模型，它通过在从片与主片间施加约束来限制物体间的相互侵入。该类模型可应用于有限变形和界面滑移分析，计算精度高，但计算量大。无论算法，还是具体实现上，该类模型都存在较大困难，目前仍处于发展阶段。

接触界面离散方式在很大程度上决定了接触界面搜索方式和接触力的计算方法。鉴于NTS模型的广泛应用，本文将针对基于该类模型发展的相关算法进行讨论。

3 接触搜索算法

如上文所述，接触界面的确定是接触-碰撞问题数值计算中最耗时的部分。如采用最直接的暴力搜索方法确定接触对，其计算量将为O(N2)，这里N为系统中的节点数。因此，暴力搜索对于实际工程问题(通常需要较多的单元离散，即N很大)几乎没有实用价值，必须寻求更高效的接触对确定算法。

为加速接触对确定，接触搜索通常分全局搜索和局部搜索两个步骤进行。全局搜索利用某些简单的准则快速排除掉系统中不可能发生接触的部位，或挑选出最可能发生接触的从点与主片对，即确定出接触测试对。局部搜索则从接触测试对中精确确定出真实发生接触的从点与主片对，即接触对。一般而言，全局搜索决定了接触计算效率；局部搜索主要影响接触计算精度，同时对计算效率也有一定影响。

典型的全局搜索算法有主从面算法[12]、桶排序法[6,8,13,17]、线性位置码算法[11]、级域算法[1,18,19]及树形算法[20-22]。局部搜索方面，常用算法有点面算法[6,12,13]、内外算法[22]、小球算法[23,24]及曲面构造法[25,26]。

3.1.1 主从面算法

主从面算法[12]是最早用于求解大规模接触-碰撞问题的接触界面搜索方法，现仍然应用于通用有限元程序，如LS -DYNA[13]、ABAQUS/Explicit[27]。与暴力搜索方法相比，主从面算法仅在事前指定的有可能发生接触的从节点集与主片集内进行接触搜索，即对每一个从节点在接触主片集内确定出与其最近的主节点，与该主节点相连的主片视为从点的潜在接触主片。

主从面算法的计算复杂度仍为O(N2)。为减小计算量，通常引入界面跟踪技术[13,28,29]，即假定当前时间步从节点的最近主节点为上一时间步确定的最近主节点或与该主节点直接相连的节点，以减少节点间距离的计算次数。

主从面算法对于含有少量接触，且事前可大致确定出接触部位的问题非常有效。但该算法只能处理两个表面间的接触，不能用于单一曲面接触，也不能用于含材料断裂破坏的侵蚀接触分析，甚至不能用于相对初始构形有严重变形的接触问题[6,13]。

3.1.2 桶排序算法

桶排序法是目前应用最广泛的全局搜索算法，该类算法的基本思想是[6,13,17],首先，根据接触系统单元的某种特征尺寸(如最大单元长度)将接触界面空间分割为若干规则的子区域(称为桶)；然后，将所有可能参与接触的节点根据其坐标排列到这些桶中；接着，根据节点所处的桶序号进行排序，形成节点的有序表；最后，对每个从节点，利用该有序表在其所处桶及相邻桶的节点中确定出距离最近的节点，该节点相连接的单元外表面与从节点构成接触测试对。

桶排序法通过将节点分组(同一桶中的节点视为一组)极大缩小了全局接触搜索范围，从而大幅提高计算效率。该算法不需要预先指定接触主从面，因此具有良好的适用性，可以用于多体接触[13]、单曲面接触[6]和侵蚀接触[17]等不同接触类型。

对三维空间问题，经典桶排序法[6]采用三层嵌套的一维桶排序实现。一维桶排序的基本原理如图2所示，根据单元特征尺寸将接触界面空间(xmin,xmax)分割为若干桶，接触只能发生在节点处于同一桶或相邻桶中的单元间。因此，为搜索到所有可能的接触对，桶的尺寸应不小于l/3，l为系统中最大单元长度。显然，这对于单元网格划分很不均匀的系统，桶最优特征尺寸的确定存在很大难度。桶越小，需要进行距离判断的节点也就越少，搜索速度越快，但桶过小可能会导致接触搜索遗漏。经典桶排序法另外一个问题就是内存需求量大[7]。

Heinstein等[7,8]引入包围盒(the bounding box)改进了桶排序算法，利用主片当前构形与预测的下一时步构形定义包围盒，根据从节点运动速度适当扩展包围盒而形成捕捉盒(the capture box)，如图3 所示；捕捉盒内的节点视为该主片的潜在接触从点。算法改进后，桶的尺寸可取为系统中最小单元的特征长度，算法效率仅依赖于从点和主片的数量，而与桶的尺寸无关。另外，该算法通过定义统一桶编号而使排序和查找在一维空间进行，从而提高了算法效率，降低了内存需要。

3.1.3 级域算法

级域算法[1,18,19]建立在接触实体层级、层域及接触域等概念的基础上。根据几何关系，接触系统可分为不同层级的实体，即接触体、接触面、接触片、接触边和接触点。接触系统由一个或多个接触体组成，一个接触体可包含若干接触面，一个接触面由多个接触片构成。

层域是某层级实体占据的空间，为避免每个迭代步都进行全局搜索，可将此区域适当扩展而形成扩展域。当从点位于某主点、线或片的接触域内时，认为该从点与相应的主点、线或片接触。点、线与片接触域的定义如图4所示。片的接触域由其边、外法线方向及某种特征厚度确定，线的接触域由其外法线方向及其所在的片厚度确定，点的接触域则由其所在线的外法线方向及相应片厚度确定。

接触搜索时，先在较高级的层域间进行，若两个域存在重叠，则继续进行下一级层域的相交检查，直至确定出接触测试对；若两域不存在重叠，则两接触实体间不存在接触关系，接触搜索停止。

级域算法利用了接触体的层级结构，在较高级实体中排除了不必要的接触检查，理论上可大幅提高接触搜索效率，这对于同级域重叠部分较小的接触问题非常有效。但对于同级实体存在较多重叠的接触问题，如单曲面接触，计算效率不如位置码算法[30]。另外，程序实现方面，由于该类算法涉及不同层级接触实体的定义及相应的数据管理，程序设计与实现都很繁琐。

图2 一维桶排序示意图

Fig.2 Illustration of bucket sorting in 1D

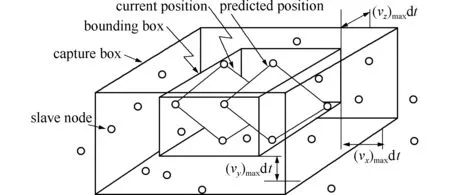
图3 主片的包围盒与捕捉盒[8]

Fig.3 Bounding box and capture box for a master segment[8]

3.1.4 位置码算法

Oldenburg等[11]在桶排序和级域算法基础上建立了位置码算法。该算法对每一个主片首先确定位于其片域内的接触从点；对位于主片域内的从点进一步检查是否处于主片接触域内，接触域内的从点与主片构成接触测试对。接触域和片域的二维图如图5所示。

定义了主片域后，位于主片域内从点的三维空间搜索利用位置码转换到一维空间中进行：接触界面空间分割成若干桶；根据节点所在的桶，对每一个节点赋予一个位置码；根据位置码与节点坐标将三维空间中的节点排序到一维数组(称为位置码向量)；对每一个主片，确定出主片域占据的桶，利用二分查找算法在位置码向量中找出这些桶中的节点(潜在接触从点)。同时，位置码算法采用层级概念定义了三层接触实体，即接触面、接触片和接触点，每一个接触面定义一个位置码向量。

位置码算法将三维空间的节点排序和搜索映射到一维数组中进行，并利用二分查找法加速接触从点的搜索速度，具有很高的计算效率(计算复杂度为O(Nlog2N))。并且，该算法无需区分主从面接触和单曲面接触，通用性强。

位置码算法的效率有一定的网格方向依赖性，这是由桶的编码方式决定的。Diekmann等[30]以空间填充曲线法SPC(Space Filling Curve algorithm)代替逐行扫描的桶编码方式，改进了位置码算法。在处理细长结构或复杂结构间的接触时，SPC算法具有更高的计算效率。

3.1.5 树形算法

树形算法是新近发展的一类全局搜索方法。

图4 点、线和片的接触域

Fig. 4 Contact territories of a node,an edge and a segment

图5 接触域和片域的定义

Fig.5 Conception of contact territory and segment territory

该方法的基本思想是，采用树形数据结构，如二叉树和四叉树，存储接触片几何信息，利用树的快速遍历方法确定出有可能参与接触的从点与主片或者从片与主片对。

针对冲压成形中板料与模具间的动态接触，Bruneel等[20]以四叉树存储模具(模具表面离散为多边形几何平面)的M个接触片，建立了计算复杂度为O(Nlog4M)的QuickTrace算法。Yang等[21]针对mortar接触中的面-面接触对确定，基于层次包围盒BVH(Bounding Volume Hierarchy)发展了适用于大变形滑移接触问题的二叉树接触搜索算法；柳阳等[31]采用类似方法实现显式有限元中动态接触界面的快速搜索。

与经典桶排序算法[6,13]相比，树形算法的计算量仅与接触测试对的数量相关，而与接触系统中潜在接触对的空间分布无关[21]。另外，树形算法中子节点与父节点有层级关系，这类似于级域算法[18]中级的属性。因此，对于大规模复杂接触问题，树形算法在内存需求与计算效率方面具有较大优势。在程序实现方面，树形算法可采用递归方式设计，程序设计与代码实现都相对简单。

3.1.6 其他方法

Papadopoulos等[32]基于类似于小球算法的思想建立了所谓的球形排序算法(spherical-sorting algorithm)。该算法对于小规模或者仅含有少量接触对的问题计算效率很高，但不适用于复杂工程问题。因为该算法在每个求解步都需要对所有的潜在接触片进行距离比较和判断，当接触片较多时计算效率会远低于桶排序和位置码等接触搜索算法。

Mahadevaiah[33]耦合球形排序算法与桶排序方法建立了球形桶排序算法(sphere-bucket-sort algorithm)。该算法对每个可能参与接触的节点建立一个虚拟的包围球，将包围球排序到桶中，然后利用经典桶排序方法[6]确定出可能的接触对。该算法集成了桶排序算法与小球算法的优势，理论上具有较高的计算效率。

近年，针对离散粒子接触系统，发展了大量优秀的接触搜索算法，虽然不能直接用于有限元接触计算，但为有限元接触搜索算法的设计提供了重要借鉴。王福军等[25,34]借鉴NBS算法[35]，利用链表技术对桶排序算法进一步改进，将节点位置码排序到链表结构中，接触搜索转变为从两个一维数组中取数据的过程，计算量降低为O(N)。Chen等[36]借用CGRID算法[37]的不同尺寸粒子迁移策略，引入了层、列和方格概念，建立了计算效率不受网格尺寸影响以及内存需求与计算成本呈线性复杂度的全局搜索算法。

与全局搜索相比，局部搜索算法的研究相对较少，目前主要采用的方法有点面算法和小球类算法两大类。另有少量搜索算法主要是针对两类算法的不足而提出的改进方案，如内外算法、曲面构造法及静动态检测法等。

3.2.1 点面算法

点面算法[6](node -to-segment algorithm)是目前最常用的一类局部搜索算法，广泛应用于通用有限元程序[13,27]。该算法的计算过程为[6]，对每个从点，在与其最近主点相连的主片中确定出可能接触的主片；计算从点在该主片上的投影点(或称为接触点)；利用投影点确定从点对主片的侵入深度。

假定从点ns最近的主点为nm，与nm相连的主片为s1，s2，s3和s4，如图6所示。如果nm与ns不重合，当满足式(11)时，ns可能与主片si接触。

(ci×s)·(ci×ci +1)>0

(11a)

(ci×s)·(s×ci +1)>0

(11b)

式中ci和ci +1为过点nm的主片两边定义的向量,s为向量g在主片si上的投影，而g为连接nm和ns的向量，

s=g-(g·m)m

(12)

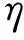
(13)

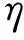
(14)

式中ni为投影方向(或侵彻方向)，

(15)

若l<0，表明从点对主片有侵入，则根据接触约束算法在从点与主片间施加接触约束力。

当接触界面光滑且网格质量较好时，点面搜索算法非常有效，这也是该方法受到广泛采用的原因。但算法存在如下不足。

(1) 经典点面算法[6,13]采用双线性参数化方程表征主片，利用Newton-Raphson迭代求解偏微分方程组(13)的方式计算接触点。该方法在大多数情况下是有效的，但当主片发生较大的翘曲变形时可能存在收敛困难和不稳定等问题[22]。

(2) 以主片外法线方向作为从点的投影方向，存在投影点不唯一或无投影点等奇异性问题[38]，即所谓的盲区(或称为死区)，如图8所示。

(3) 接触面网格质量较差时，如细长比过大，可能会发生接触搜索遗漏，如图9所示。

(4) 由于该方法侵入检查是针对从点与主片的关系进行的，因此不能处理如图10所示的边-面和面-面接触情况。

图6 从点在主片上的投影

Fig.6 Projection of the slave node onto master segment

图7 接触点的确定

Fig.7 Determination of contact point

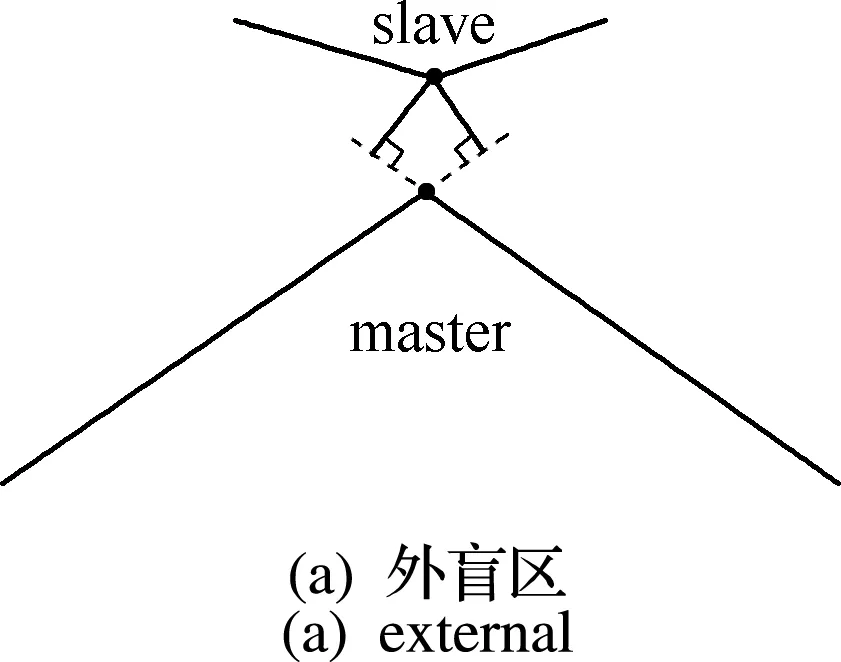
图8 两种接触搜索盲区

Fig.8 Examples of blind zones

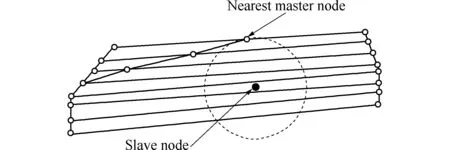
图9 网格细长比过大造成接触搜索遗漏[13]

Fig.9 Failure to find contact pairs due to poor aspect ratio in mesh[13]

3.2.2 内外算法

面向金属成形模拟，针对经典点面算法[6]接触盲区与计算效率的不足，Wang等[22]改进了从点对主片的投影方向以及接触点的计算方法，从而建立了内外算法(inside -outside -algorithm)。

内外算法中，以从点的外法线方向作为从点对主片的投影方向(同时也是接触力施加方向)。从点外法向定义为与该节点相连的接触片法线方向的平均值，如图11所示。

(16)

从点相对于主片一条边的内或外状态，通过从点与该边构成的三角形在主片上的投影来确定，如图12所示，

Δa=n·(ra b×ra d)

(17)

若Δa≤0，则从点处于边内部。如果从点处于主片所有边的内部或者外部，则从点位于该主片内部，否则位于主片外部。

图10 边-面接触和面-面接触

Fig.10 Edge -to -surface contact and surface -to -surface contact

图11 从点S的外法线方向

Fig.11 Definition of normal vector of nodeS

图12 从点的内外状态检查

Fig.12 Inside/outside checking on a 4-node segment

如果从点位于主片内部，则利用式(18)计算从点对主片的侵入量，

g=n·(x-xs)

(18)

式中x为投影点，利用式(17)可以解析给出；xs为从节点位置向量。

内外算法的优势在于，接触点可以唯一确定，避免了从点对主片的多重接触，并且接触点计算不需要迭代。因此，该算法具有很好的健壮性与较高的计算效率。由于内外算法假定接触点处主从面的法向共轴(但方向相反)，当从点位于两个低阶单元的交界线上时，尤其是当网格不够精细时，内外算法给出的接触方向可能会与实际存在较大偏差[26]。

3.2.3 构造曲面法

点面算法存在投影奇异性的根本原因是低阶有限元近似使得接触界面仅C0连续，接触片交界处接触界面外法线方向存在间断。因此，接触片光滑化是解决盲区问题的一种有效方式。构造曲面法(或称为曲面光滑化法)正是基于这种思想建立的，即基于离散的接触界面拓扑信息，采用高阶插值函数重构接触面，使新接触面外法线方向空间连续分布。

构造曲面法不仅可以克服接触盲区，也有利于提高接触力计算精度，消除接触滑移时接触力的非物理震荡。关于构造曲面法，已有很多学者开展相关研究，提出了一些光滑化算法，如三次样条法[39]、NURBS法[40]、Gregory片法[41]和FFS算法[25,26](Free -Formed-Surface algorithm)等。其中，FFS法建立的曲面有C1连续性，可用于三维问题，且无需引入额外边界定义或额外自由度。

FFS方法利用接触片节点坐标构造参数化光滑曲面片。如图13所示，任意一个由四条边构成的接触片，参数化光滑曲面可表示为

(19)

式中x为曲面的整体坐标，u和w为曲面的局部坐标，ci j为参数向量，可根据相关节点坐标确定。两节点间的边界线利用相邻节点坐标以分段三次Hermite曲线构造，从而保证了相邻接触片间的连续。

FFS算法构造的曲面具有C1连续性，接触点与接触方向计算精度高，很大程度上克服了接触盲区问题。算法的不足是计算量增加较多，尤其是接触片畸变较大时,需要将接触片进行多次子片剖分才能得到满足精度的结果。

3.2.4 静动态检测法

经典点面局部搜索算法[6]仅利用主片和从点的当前位置信息确定接触状态，对于发生穿透的从点，沿主片外法线方向施加接触力将其外推至主片上。这可能会导致接触主片判断错误或从点回退方向(也就是接触力方向)不正确等问题，为此Heinstein等[7,8]提出了静动态检测算法。该算法对于上一时间步已经处于接触状态的从点采用静态检测法确定当前接触状态；对上一时间步未发生接触，但在当前时间步发生接触的从点采用动态接触检测。

(1) 动态检测。根据从点和主片的当前位置及下一时间步的预测速度，利用从点和主片接触时刻的共面关系，确定出接触时刻与接触点。三维情况下，这种接触检查简化为判断一个移动三角形和一个移动点之间的接触问题(对于四边形主片，可以利用主片中心点与四个边将主片分解为四个三角形)，如图14所示。求得接触时刻与接触点后，进一步判断接触时刻是否满足步长稳定性要求，及接触点是否位于主片内部，如满足则发生接触。

3.2.5 小球算法与分裂小球算法

小球算法(pinball algorithm)是Belytschko等[23]为适应高速撞击和侵彻接触计算向量化需求

图13 自由曲面的构造

Fig.13 Construction of FFS

图14 基于速度的动态接触检查

Fig.14 Contact checking based on velocity

提出的一种高效接触算法。该算法的核心思想是以单元内嵌小球(称为等效小球)代替可能参与接触的表面单元，单元间的侵入检查与接触约束转化为小球之间的距离判断与约束施加。等效小球的体积为相应单元的体积，并假定变形过程中保持不变，球心为单元各节点坐标的平均值。小球概念的二维示意如图17所示。

引入小球概念后，单元间的侵入检查变得极为简单。假定主面单元与从面单元等效小球的半径分别为R1和R2，球心位置矢量为C1和C2。当两个小球球心距离d满足式(20)时，认为两单元发生接触。

d

(20)

侵入深度g由式(21)计算得到，

dTd=(R1+R2)2

(21)

式中d=C1-C2+gn，n=(n2-n1)/‖n2-n1‖，n1和n2分别为主片与从片的外法线方向。

小球算法可用于实体单元或薄壳单元的任意类型接触分析。但用于薄壳单元时，若壳元厚度相对于其特征尺寸很小，则小球算法精度会非常差；若壳单元间存在初始接触，小球算法可能会失效。为此，Belytschko等[24]在小球算法基础上发展了分裂小球算法(splitting pinball method)。

与小球算法类似，分裂小球算法以小球代替每一个参与接触的表面单元，但小球的半径要足够大以完全覆盖相应单元，该小球称为父球。父球间若有重叠区则表示两单元间可能存在接触，此时父球分裂为下一级的子球进一步作重叠区检查，直至最后一级子球的半径与壳厚度相当。四边形壳元的小球层级如图18所示，接触检查与小球逐级分裂的一维示意如图19所示。

图15 从点对凹面侵彻

Fig.15 Contact checking for a concave surface

图16 从点对凸面的侵彻

Fig.16 Contact checking for a convex surface

小球算法和分裂小球算法以统一的方式自动处理边-边、边-面及面-体等接触类型，算法便于向量化和并行计算；单元间的接触检查与侵入量计算简单高效。小球算法和分裂小球算法适用于碰撞和侵彻等问题的模拟。由于算法未考虑接触界面间的摩擦效应，不能应用于滑移和摩擦为关键因素的接触分析中。另外，当接触界面单元特征尺寸差别较大时，接触力的计算精度较差，不准确的几何近似和小球体积不变假设限制了该算法的应用[7]。

4 接触约束算法

接触约束算法，也称为接触力算法，基本方法有拉氏乘子法和罚函数法[1,4]。基于这两类方法，还发展了增广拉氏乘子法和摄动拉氏乘子法。拉氏乘子类方法计算格式与显式有限元计算不相容，不能直接用于显式有限元的接触分析，罚函数法是目前显式有限元程序的主要方法。

罚函数法的基本原理是，如果从点对主片没有侵入则不做处理；如果从点侵入主片，则在从点与主片间引入法向接触力，将从点推回到变形后的接触主片上，以满足不可侵入条件。

图17 平面单元的内嵌小球

Fig.17 Embedded pinball in two dimensions

图18 四边形薄壳单元的小球层级

Fig.18 Pinball hierarchy of 4-node shell element

图19 一维单元的接触检查

Fig.19 Contact detection using pinballs

罚函数法不增加系统方程的自由度数，接触力计算无需联立求解方程组，程序实现简单且计算效率高，广泛应用于显式有限元程序中，如 LS -Dyna[13]，Abaqus/Explicit[27]和Pronto3D[42]等。罚函数法最大的不足在于不可侵入条件只能近似满足，计算精度严重依赖于罚因子的选取，而罚因子取值往往依赖于使用者的经验。

通用程序一般会对罚因子进行规则化处理，以便用户选取相对合理的罚参数。以LS -Dyna[13]为例，作用于从点的法向接触力为

fs=-lkini

(22)

式中l为从点对主片的侵入深度

(23)

式中ni,t和r等变量的定义见3.2.1节。其中ki即为罚因子。LS -Dyna利用主片面积Ai，主片所在单元体积Vi及材料体积模量Ki对其规则化

(24)

规则化后的接触罚参数fSI取值范围通常为 (0.0,1.0]。得到从点的接触力后，根据牛顿第三定律，作用在主片接触点上的力为-fs，按照式(25)可将该合力分配到主片各节点上，

(25)

拉氏乘子法中，以接触对间的接触力作为乘子来限制接触体间的相互侵入，不可侵入条件可精确满足。但该方法引入了新的未知变量，增加了方程组的自由度数；接触力计算需要联立方程求解，这与显式有限元计算不相容。为了在显式有限元中应用乘子法进行接触力计算，必须对经典的拉氏乘子法做必要的格式修正。

Carpenter等[43]利用上一时间步的乘子与本步的位移建立接触约束方程，采用修正高斯-塞得尔迭代法求解拉氏乘子，建立了二维接触问题的前增量拉氏乘子法(forward increment Lagrange multiplier)。Sha等[44]在前增量位移中心差分方法(forward incremental displacement-central difference method)基础上，建立了接触约束的线性补充方程，并给出了改进的共轭梯度求解算法。Zhong[1]提出了防御节点法(defense node algorithm)；王福军等[45]考虑相邻接触点间的相互影响，在防御节点法基础上建立了局部拉氏乘子方法；Chen等[46]对初始碰撞和后续接触采用不同的接触约束方程，并利用高斯-塞得尔迭代法求解拉氏乘子。这些方法中，防御节点法不需要任何迭代，计算效率高，是乘子类方法在显式有限元中成功应用的典范。

防御节点法的基本思想是，将从点与主片之间的接触作用转化为从点与防御节点之间的接触，防御节点携带了主片的运动学与动力学信息，如位移、速度及节点力等。防御节点位于接触点，表征主片的运动，因此其速度和加速度可以利用主片的节点速度和加速度描述，F为除接触力以外的力，f为从点与防御节点间的接触力。计算f时，施加不可侵入条件。得到f后，接触力就可以分布到主点上。

(26，27)

Ma=F+f

(28)

5 接触-碰撞问题的并行计算

接触-碰撞问题通常采用显式有限元进行计算。显式虽然避免了内存的庞大需求，但积分稳定性要求时间步长必须足够小，这导致接触-碰撞问题求解通常需要大量迭代，对于大规模或复杂几何构形问题非常耗时，因此并行计算是接触-碰撞数值分析的必然选择。

区域分解(spatial domain decomposition method)是实现接触-碰撞问题大规模并行计算的最有效方式。区域分解的基本思想[47]是，将一个复杂系统按照一定的准则(如物理特性或几何形状)划分为一系列子系统(称为子区域)；将子区域分配到各个处理器上分别处理；子区域间通过消息传递协同计算，最终求得原问题的解。区域分解可以为大规模问题提供高度并行且可扩展的健壮算法。

与不含接触的动力学问题或准静态接触问题不同，接触-碰撞问题的接触域通常具有全局性与动态性，计算节点之间的通信关系在系统求解之前不能确定。如图20所示的一个简单接触问题，开始时刻下方物体上表面的左前部位与上面物体发生接触，而在某个时刻下方物体上表面的右后部位与上面物体发生接触。接触界面的全局性和动态性对接触-碰撞问题的区域分割和计算节点间的通信关系设计带来极大挑战。

(1) 对有限元计算(主要是内力计算)高效的某种区域分解在接触计算中往往不能取得好的并行性能，通常需要针对接触而引入另外的区域分割。

(2) 动态接触的全局性导致计算节点间存在大量的数据交互，最大限度地减小通信量才能保证算法的扩展性与并行效率。

(3) 接触对动态变化，局部接触搜索和约束施加在不同时刻可能由不同的计算节点完成，极易造成各节点机负载的不均衡。

基于区域分解的并行接触算法研究始于20世纪90年代。Malone等[48,49]基于体积检测，通过引入接触域(contact domain)实现接触搜索的本地计算，设计了可应用于三维壳体结构计算的并行接触-碰撞算法。Waston等[50]针对简单接触问题，设计了基于单元分解的并行算法；Zhong等[51]针对Connection Machine机型，设计了基于桶排序的并行接触算法；Har等[52]针对薄壳单元结构，设计了三维桶排序并行算法，利用IBM SP2的10个处理器进行了接触并行计算；陈成军等[53,54]开展了类似工作；文献[55-58]提出了双层次区域分解方案(dual-level domain decomposition scheme)，利用8个处理器实现了32万自由度的冲击接触问题并行计算；金先龙等[59,60]基于坐标递归二分法RCB(Recursive Coordinate Bisection algorithm)设计了接触均衡分区算法CBB(Contact Balance Bisection algorithm)，并在曙光4000A上利用16个CPU进行了汽车碰撞安全性数值模拟以及轻轨列车-斜拉桥耦合振动响应分析，但该算法仅适用于接触界面事前可以确定的问题；Paik等[61]利用不规则通信重构从节点集，发展了并行接触算法，利用256个处理器进行了球撞击平板的模拟。

上述算法仅适用于少量CPU核的集群环境，有良好扩展性、适用于大型并行系统(数千CPU核)的并行接触算法研究还较少。目前该方面的研究主要限于美国Sandia国家实验室[62,63]、Livermore实验室[64-66]及中国工程物理研究院[67,68]等少量团队。Sandia实验室的Attaway等[62，63]于1998年使用PRONTO3D程序在Sandia/Intel TFLOPS并行机上实现了薄壁柱壳动态屈曲至完全压溃模拟的3600个计算节点并行，2000年利用3504个计算节点模拟了包含六百多万个单元的包装箱碰撞和压溃响应。最近，中国工程物理研究院总体工程研究所陈成军等[68]利用8192 CPU核实现了16.1亿自由度规模的并行接触计算。需要特别指出的是，近年一些商业程序，如LS -DYNA等，也开始致力于并行版本的开发[69-71]。

图20 动态接触示意图

Fig.20 Illustration of dynamic contacting

基于区域分解实现接触-碰撞问题的粗粒度并行有单一区域分解法和双重区域分解法两种并行方案。双重区域分解法中，有限元计算采用一种子域剖分(称为主分区)，接触计算采用另外一套分区(称为次分区)；而单一区域分解法，接触区域不作单独的子区分割，接触的并行计算基于主分区进行。通常，双重区域分解法可获得更好的负载均衡，但节点机间的通信复杂；单一分区法通信拓扑简单，但易导致负载不均衡。

单一区域分解方法中，接触计算的并行基于主分区进行。接触算法并行的关键在于，每个计算节点可有效得到本地计算所需的全部信息。因此，该类算法通常引入影像区(ghost)或接触域(contact domain)存储本地接触计算需要但驻留在其他节点机上的信息。

基于单一区域分解的并行接触算法设计相对简单，本文以Malone等[49]的工作为例简要描述该类算法的实现方式。

(1) 不考虑接触界面，对求解域作区域剖分，分配给各计算节点。所有计算节点作如下相同的计算。

(2) 对任意计算节点PA，构建覆盖该计算节点单元几何空间的包围盒(bounding box)，并传递到其他计算节点，同时接收其他计算节点的包围盒信息。

(3) 利用体积检查(volume checking)判断PA包围盒与其他包围盒是否有重叠。若无重叠，则两个计算节点的单元间无潜在接触；若有重叠部分，则将与PA包围盒有重叠的计算节点上的单元信息收集到PA的接触域，同时将PA单元传递给对方计算节点的接触域。

(4) 对每个计算节点利用串行接触算法进行接触计算(全局搜索、局部接触和约束施加)。

基于单一静态区域剖分的并行接触算法概念简单，程序实现容易。由于引入影像区存储本地计算所需的全部信息，不需要每步计算都进行数据通信。但由于区域剖分时未考虑接触计算的影响，容易导致计算节点间严重的负载不均衡，算法并行扩展性差[62]，很难扩展到数千CPU核。

双重区域分解方法中，单元计算和接触计算分别基于主分区和次分区进行。主分区通常采用图剖分法进行区域分割，次分区采用几何剖分方法。基于双重分区的并行接触算法通信拓扑较为复杂，通常需要每步计算在主分区与次分区间进行数据交互，但该类方法可以较好地实现负载平衡。

基于双重区域分解的并行接触算法以圣地亚实验室Attaway等[63,64]的工作最为典型。他们对有限元计算采用静态图剖分方法，接触界面区域采用动态RCB算法作区域分割，大致保证了每个计算节点有相同的接触从点和接触主片，算法有效扩展至数千CPU核。图21给出了该算法的基本计算流程。

1.Send contact data from FE decomposition to old RCB decomposition

2.Perform parallel RCB to rebalance

3.Share RCB cut information with all processors

4.For all my surfaces

IF surface capture box extends beyond my RCB box,THEN

Determine which other processors need it

END IF

5.Send overlapping surfaces to nearby processors

6.Find contacts within corresponding RCB Box

CALL global search and local search routines

7.Send contact searching results to FE owners

图21 并行接触计算的区域分割

Fig.21 Outline of dynamic decomposition for parallel contacts

6 结 论

本文总结分析了显格式有限元计算常用的接触-碰撞算法，包括全局搜索、局部搜索、约束施加算法以及基于区域分解的并行计算方法。本文可为接触-碰撞算法的深入研究提供基础的理论参考。

接触-碰撞算法，特别是局部接触搜索算法，实现细节非常丰富。看似可忽略的细节常常决定了算法的健壮性与精度，程序实现时必须予以充分考虑。

经30多年的发展，接触-碰撞算法已经能够解决大多数的工程问题，但仍然存在一些问题需要进一步深入研究。

(1) 局部搜索精度。目前，接触-碰撞算法主要是基于点-面接触模型发展起来的，相关算法相对简单且效率高，但在处理不连续、非光滑接触界面时易发生接触遗漏，死区仍然是一个没有完全解决的难点。面-面接触模型有望避免涉及死区问题，基于面-面接触模型发展相应的接触搜索算法是接触-碰撞问题数值算法的一个研究重点。

(2) 全局搜索效率。全局搜索是影响接触-碰撞问题数值计算效率的关键因素。目前已有全局搜索算法仍不能满足计算需求，仍然需要发展高效的搜索算法。

(3) 并行扩展性。接触-碰撞并行算法设计的关键在于全局搜索算法。目前，接触搜索算法大多是针对串行计算而设计，缺乏内在并行性。动态接触界面的动态性、全局性与事先不确定性特点决定了并行计算时常需要大量的全局通信及不规则的通信拓扑。另外，接触系统中实际发生接触的部位往往是局部的，极易导致节点机的严重负载不平衡。这些因素使得接触-碰撞并行算法的设计极具挑战性，可用于数千CPU核的并行接触算法仍处于发展中。

:

[1] Zhong Z H.FiniteElementProceduresforContact-ImpactProblems[M].New York:Oxford University Press,1993.

[2] Laursen T A.ComputationalContactandImpactMechanics[M].Berlin:Springer,2002.

[3] Yastrebov V A.NumericalMethodsinContactMechanics[M].John Wiley & Sons,2013.

[4] Belytschko T,Liu W K,Moran B,et al.NonlinearFiniteElementsforContinuaandStructures[M].John Wiley & Sons,2013.

[5] Shukla A，Ravichandran G,Rajapakse Y.DynamicFailureofMaterialsandStructures[M].New York：Springer,2010.

[6] Benson D J,Hallquist J O.A single surface contact algorithm for the post-buckling analysis of shell structures [J].ComputerMethodsinAppliedMechanicsandEngineering,1990,78(2):141-163.

[7] Heinstein M W,Attaway S W,Swegle J W,et al.A General-Purpose Contact Detection Algorithm for Nonlinear Structural Analysis Codes [R].SAND92-2141,Sandia National Laboratories,Albuquerque,1993.

[8] Heinstein M W,Mello F J,Attaway S W,et al.Contact-impact modeling in explicit transient dynamics [J].ComputerMethodsinAppliedMechanicsandEngineering,2000,187(3-4):621-640.

[9] Bourago N G,Kukudzhanov V N.A review of contact algorithms [J].MechanicsofSolids,2005,40(1):35-71.

[10] 钟 阳,钟志华,李光耀,等.机械系统接触碰撞界面显式计算的算法综述 [J].机械工程学报,2011,47(13):44-58.(ZHONG Yang,ZHONG Zhi-hua,LI Guang-yao,et al.Review on Contact algorithms calculating the contact-impact interface in mechanical system with explicit FEM [J].JournalofMechanicalEngineering,2011,47(13):44-58.(in Chinese))

[11] Oldenburg M,Nilsson L.The position code algorithm for contact searching [J].InternationalJournalforNumericalMethodsinEngineering,1994,37(3):359-386.

[12] Hallquist J O,Goudreau G L,Benson D J.Sliding interfaces with contact-impact in large -scale Lagrangian computations [J].ComputerMethodsinAppliedMechanicsandEngineering,1985,51(1):107-137.

[13] Hallquist J O.LS-DYNATheoryManual[M].Livermore Software Technology Corporation,2006.

[14] Hughes T J R,Taylor R L,Sackman J L,et al.A finite element method for a class of contact-impact problems [J].ComputerMethodsinAppliedMechanicsandEngineering,1976,8(3):249-276.

[15] Puso M A,Laursen T A.A mortar segment-to -segment contact method for large deformation so -lid mechanics [J].ComputerMethodsinAppliedMechanicsandEngineering,2004,193(6):601-629.

[16] Laursen T A,Puso M A,Sanders J.Mortar contact formulations for deformable -deformable contact:past contributions and new extensions for enriched and embedded interface formulations[J].ComputerMe-thodsinAppliedMechanicsandEngineering,2012,205:3-15.

[17] Belytschko T,Lin J I.A three -dimensional impact-penetration algorithm witherosion [J].Computers&Structures,1987,5(1-4):111-127.

[18] Zhong Z H,Nilsson L.A contact searching algorithm for general contact problems [J].Computers&Structures,1989,33(1):197-209.

[19] Zhong Z H,Nilsson L.A unified contact algorithm based on the territory concept [J].ComputerMethodsinAppliedMechanicsandEngineering,1996,130(1-2):1-6.

[20] Bruneel H C J,De Rycke I.QuickTrace:a fast algorithm to detect contact [J].InternationalJournalforNumericalMethodsinEngineering,2002,54(2):299-316.

[21] Yang B,Laursen T A.A contact searching algorithm including bounding volume trees applied to finite sliding mortar formulations [J].ComputationalMechanics,2008,41(2):189-205.

[22] Wang S P,Nakamachi E.The inside -outside contact search algorithm for finite element analysis [J].InternationalJournalforNumericalMethodsinEngineering,1997,40(19):3665-3685.

[23] Belytschko T,Neal M O.Contact-impact by the pinball algorithm with penalty and Lagrangian methods [J].InternationalJournalforNumericalMethodsinEngineering,1991,31(3):547-572.

[24] Belytschko T,Yeh I S.The splitting pinball method for contact-impact problems [J].ComputerMethodsinAppliedMechanicsandEngineering,1993,105(3):375-393.

[25] 王福军.冲击接触问题有限元法并行计算及其工程应用 [D].清华大学,2000.(WANG Fu-jun.Parallel Computation of Contact-Impact Problems with FEM and Its Engineering [D].Tshinghua University,2000.(in Chinese))

[26] Wang F J,Cheng J G,Yao Z H.FFS contact sear-ching algorithm for dynamic finite element analysis [J].InternationalJournalforNumericalMethodsinEngineering,2001,52(7):655-672.

[27] Abaqus 6.12TheoryManual[M].Dassault Systemes Simulia Corporation,2012.

[28] Whirley R G,Engelmann B E.Automatic Contact in DYNA3D for Vehicle Crashworthiness [R].Lawrence Livermore National Laboratories,CA,1993.

[29] Whirley R G,Engelmann B E.Automatic contact algorithm in DYNA3D for crashworthiness and impact problems [J].NuclearEngineeringandDesign,1994,150(2):225-233.

[30] Diekmann R,Hungershofer J,Lux M,et al.Efficient contact search for finite element analysis [A].European Congress on Computational Methods in Applied Sciences and Engineering[C].Barchlona,Spain,2000.

[31] 柳 阳,柳 明,陈成军.简化相邻依赖关系的mortar面面接触算法研究[A].中国计算力学大会[C].贵阳,2014.(LIU Yang,LIU Ming,CHEN Cheng-jun.Investigation of the mortar segment-to-segment contact algorithm with the neighbor-dependent relationship simplified[A].China Computational Mecha-nics Conference[C].Guiyang，2014.(in Chinese))

[32] Papadopoulos P,Taylor R L.A simple algorithm for three -dimensional finite element analysis of contact problems [J].Computers&Structures,1993,46(6):1107-1118.

[33] Mahadevaiah U.Development Andvalidation of New Algorithms to Improve Contact Detection and Robustness in Finite Element Simulations [D].The George Washington University,2009.

[34] Wang F J,Cheng J G,Yao Z H.A contact searching algorithm for contact-impact problems [J].ActaMechanicaSinica,2000,16(4):374-382.

[35] Munjiza A,Andrews K R F.NBS contact detection algorithm for bodies of similar size [J].InternationalJournalforNumericalMethodsinEngineering,1998,43(1):131-149.

[36] Chen H,Lei Z,Zang M Y.LC-Grid:a linear global contact search algorithm for finite element analysis [J].ComputationalMechanics,2014,54(5):1285-1301.

[37] Williams J R,Perkins E,Cook B.A contact algorithm for partitioning N arbitrary sized objects [J].EngineeringComputations,2004,21(21314):235-248.

[38] Zavarise G,De Lorenzis L.The node -to -segment algorithm for 2D frictionless contact:classical formulation and special cases[J].ComputerMethodsinAppliedMechanicsandEngineering,2009,198(41):3428-3451.

[39] EI-Abbasi N,Meguid S A,Czekanski A.On the mo -delling of smooth contact surfaces using cubic splines[J].InternationalJournalforNumericalMethodsinEngineering,2001,50(4):953-967.

[40] Corbett C J,Sauer R A.NURBS -enriched contact finite elements[J].ComputerMethodsinAppliedMechanicsandEngineering,2014,275:55-75.

[41] Puso M A,Laursen T A.A 3D contact smoothing method using Gregory patches[J].InternationalJournalforNumericalMethodsinEngineering,2002,54(8):1161-1194.

[42] Tylor L M,Flanagan D P.PRONTO 3D:A Three -Dimensional Transient Solid Dynamics Program [R].Sandia National Lab.Albuquerque,1989.

[43] Carpenter N J,Taylor R L,Katona M G.Lagrange constraints for transient finite element surface contact [J].InternationalJournalforNumericalMethodsinEngineering,1991,32(1):103-128

[44] Sha D,Tamma K K,Li M.Robust explicit computational developments and solution strategies for impact problems involving friction[J].InternationalJournalforNumericalMethodsinEngineering,1996,39(5):721-739.

[45] Wang F J,Wang L P,Cheng J G,et al.Contact force algorithm in explicit transient analysis using finite -element method [J].FiniteElementsinAnalysisandDesign,2007,43(6):580-587.

[46] Chen H,Zhang Y X,Zang M Y,et al.An explicit Lagrange constraint method for finite element analysis of frictionless 3D contact/impact problems [J].AppliedMechanicsandMaterials,2014,553:751-756.

[47] 金先龙,李渊印.结构动力学并行计算方法及应用[M].北京：国防工业出版社,2008.(JIN Xian-long,LI Yuan-yin.ParallelCalculationMethodandApp-licationofStructuralDynamics[M].Beijing:National Defence Industry Press,2008.(in Chinese))

[48] Malone J G,Johnson N L.A parallel finite element contact/impact algorithm for non-linear explicit transient analysis:Part I—The search algorithm and contact mechanics [J].InternationalJournalforNumericalMethodsinEngineering,1994,37(4):559-590.

[49] Malone J G,Johnson N L.A parallel finite element contact/impact algorithm for non-linear explicit transient analysis:Part II—Parallel implementation [J].InternationalJournalforNumericalMethodsinEngineering,1994,37(4):591-603.

[50] Watson B C,Noor A K.Large -scale contact/impact simulation and sensitivity analysis on distributed-memory computers [J].ComputerMethodsinAppliedMechanicsandEngineering,1997,141(3):373-388.

[51] Zhong Z H,Nilsson L.Contact-impact algorithms on parallel computers [J].NuclearEngineeringandDesign,1994,150(2):253-263.

[52] Har J,Fulton R E.Aparallel finite element procedure for contact-impact problems [J].EngineeringwithComputers,2003,19(2):67-84.

[53] 白小勇,何颖波,陈成军.显式有限元中的一种并行接触算法[J].计算物理,2011,28(3):341-346.(BAI Xiao -yong,HE Ying-bo,CHEN Cheng-jun.A parallel contact detection algorithm for explicit finite element analysis [J].ChineseJournalofComputationalPhysics,2011,28(3):341-346.(in Chinese))

[54] 陈成军,柳 阳,张元章,等.基于PANDA的并行显式有限元程序开发[J].计算力学学报,2011,28(s1):204-207，214.(CHEN Cheng-jun,LIU Yang,ZHANG Yuan-Zhang,et al.Programming of parallel explicit finite element based on PANDA [J].ChineseJournalofComputationalMechanics,2011,28(s1):204-207，214.(in Chinese))

[55] 寇哲君,程建钢,姚振汉.可扩展的冲击-接触并行计算研究[J].计算力学学报,2003,20(3):325-328.(KOU Zhe -jun,CHENG Jian-gang,YAO Zhen-han.Study of scalable parallel computation for contact-impact problems [J].ChineseJournalofComputationalMechanics,2003,20(3):325-328.(in Chinese))

[56] Wang F J,Feng Y T,Owen D R J.Interprocessor communication schemes in parallel finite -discrete element analysis on PC clusters [J].EngineeringComputations,2003,20(8):1065-1084.

[57] Wang F J,Feng Y T,Owen D R J.Parallelisation for finite -discrete element analysis in a distributed-memory environment [J].InternationalJournalofComputationalEngineeringScience,2004,5(1):1-23.

[58] 王福军,王利萍,程建钢,等.并行有限元计算中的接触算法[J].力学学报,2007,39(3):422-427.(WANG Fu-jun,WANG Li-ping,CHENG Jian-gang,et al.A contact algorithm for parallel computation of FEM [J].ChineseJournalofTheoreticalandAppliedMechanics,2007,39(3):422-427.(in Chinese))

[59] 亓文果,金先龙,张晓云.冲击-接触问题有限元仿真的并行计算[J].振动与冲击,2006,25(4):68-72.(Qi Wen-guo,JIN Xian-long,ZHANG Xiao -yun.Study on parallel algorithm for finite element simulation of contact-impact problems [J].JournalofVibrationandShock,2006,25(4):68-72.(in Chinese))

[60] 杜新光,金先龙,陈向东.基于并行计算的大跨度斜拉桥行车安全分析[J].振动与冲击,2010,29(7):5-8,78.(DU Xin-guang,JIN Xian-long,CHEN Xiang-dong.Simulation analysis for running safety of a light-rail train on a long span cable -stayed bridge based on parallel computation [J].JournalofVibrationandShock,2010,29(7):5-8,78.(in Chinese))

[61] Paik S H,Moon J J,Kim S J,et al.Parallel perfor-mance of large scale impact simulations on Linux cluster super computer [J].Computers&Structures,2006,84(10):732-741.

[62] Attaway S W,Hendrickson B A,Plimpton S J,et al.A parallel contact detection algorithm for transient solid dynamics simulations using PRONTO3D [J].ComputationalMechanics,1998,22(2):143-159.

[63] Brown K,Attaway S,Plimpton S,et al.Parallel stra-tegies for crash and impact simulations [J].ComputerMethodsinAppliedMechanicsandEngineering,2000,184(2-4):375-390.

[64] Hoover C G,Groot A J,Sherwood R J.Parallel Contact Algorithms for Explicit Finite Element Analysis [R].UCRL-JC-130461,Lawrence Livermore National Lab.Livermore,CA,1998.

[65] Pierce T G.A Parallel Algorithm for Contact in a Finite Element Hydrocode [R].Lawrence Livermore National Lab.Livermore,CA,2003.

[66] Pierce T,Rodrigue G.A parallel two -sided contact algorithm in ALE3D [J].ComputerMethodsinAppliedMechanicsandEngineering,2005,194(27-29):3127-3146.

[67] 陈成军,柳 明.大规模并行显式有限元软件开发[R].GF-A0188466G,中国工程物理研究院,2015.(CHEN Cheng-jun,LIU Ming.Development of Large Scale Parallel Explicit Finite Software[R].GF-A0188466G,China Academy of Engineering Physics,2015.(in Chinese))

[68] 肖永浩.冲击-接触问题的并行计算研究[D].中国工程物理研究院,2013.(XIAO Yong-hao.Parallel Computing Research on Impact-Contact Problems [D].Chinese Academy of Engineering Physics,2013.(in Chinese))

[69] Lin Y Y,Wang J.Performance of the hybrid LS -DYNA on crash simulation with the multicore architecture[A].7t hEuropean LS -DYNA Conference[C].2009.

[70] Makino M.The performance of 10-million element car model by MPP version of LS -DYNA on fujitsu PRIMEPOWER [A].10t hInternational LS -DYNA Users Conference[C].Michigan，2008.

[71] Kenshiro K,Mitsuhiro M.The performance of car crash simulation by LS -DYNA hybrid parallel version on fujitsu FX1 [A].11t hInternational LS -DYNA Users Conference[C].2010.