“4E”级宽扁型江海直达船结构安全可靠性探析

裴志勇 朱 波 吴卫国

(武汉理工大学交通学院1) 武汉 430063) (武汉理工大学高性能舰船技术教育部重点实验室2) 武汉 430063)

0 引 言

船舶大型化是当前航运市场主要趋势，大型船舶有较高的运输效率、较低的能源消耗，从而有良好的经济性，在严酷的市场环境中具有竞争优势[1].但由于长江是自然航道，船长、吃水受限，型深受桥梁净空高制约，大型化唯有增加船宽，开发适应长江自然条件的宽扁型船舶.

以载量大、油耗低、节能环保、经济高效为目标开发出武汉-宁波舟山航线“4E”级(节能energy-saving、环保environment-friendly、经济economy、高效efficient)宽扁型江海直达集装箱船开发过程中，宽扁船型设计加上货舱采用长大开口使得其总纵强度较弱，在海段遭遇到恶劣海况时引起船体结构破坏的概率增加.柴俊凯[2]通过改变12 400 t江海直达船关键区域的材料属性与板厚从而进行优化分析，得到了提高船体极限强度的有效途径.傅何琪[3]提出了一种解析方法用以评估破损状态下江海通航干货船的船体纵向构件的损失程度. Nilva等[4]对江海通航集装箱船在损失部分船体纵向构件下的船体剩余强度进行了分析.Nilva[5]对具有长、大开口的江海直达货船在弯扭载荷下的极限承载能力进行了分析，探讨了复合载荷下船体极限强度随开口尺寸增大的变化规律，但缺乏对宽扁船型的结构特性研究.

本文从作用于宽扁型江海直达船体的载荷和船体结构极限承载能力两方面进行计算分析，对开发船的结构安全可靠性进行评估，从而明确船体的安全裕度，使其能安全可靠使用.

1 船体结构极限强度

船体结构极限强度是指其具有的最大承载能力，如果船舶遭受的外载荷比船体结构极限强度大，则会发生船体崩溃，导致海难海损事故发生.因此，极限强度计算是保证船体结构安全可靠的重要内容.

通常计算船体结构极限强度的方法有直接计算法和逐次崩溃分析法.直接计算法是面向设计的方法，包括线弹性方法、经验公式法以及解析方法等.线弹性方法简单易用，但结构屈曲后不再保持线性关系，故该法精度不高，仅在设计初期估算极限强度的大致范围；经验公式法是由有限的数据推导而来，仅对常规、通用的已有船型有较好的结果；解析方法通过假设船体剖面在极限状态时的应力分布，考虑屈曲和屈服的影响，用理论方法得出船体梁的极限强度，其计算精度很大程度上取决于假设的极限状态船体剖面应力分布.逐次崩溃分析法着眼于结构崩溃全过程，可考虑构件失效的先后顺序以及极限强度后承载能力的降低，其最大承载能力即为结构的极限强度.逐次崩溃分析法包括简易方法如Smith法、非线性有限元法(NFEM)[6]和理想结构单元法(ISUM)[7]等.

非线性有限元法可以很好的模拟结构的屈曲/屈服行为，但一般需要较细的网格、较多的单元才能得到合理可靠的结果，对于船体梁这样的大型结构系统而言，往往由于计算时间过长而无法实际上实施.理想结构单元法是将结构的非线性行为理想化并包括在单元中，这样可以将较大的几何单位(如加强筋间的板格)视作一个理想结构单元，从而减少计算工作量；其计算精度很大程度上取决于单元理想化的合理程度.Smith法是将船体剖面离散成板和加筋板单元，考虑极限强度后承载能力的降低和崩溃的先后顺序，来揭示弯曲载荷下船体梁的逐次崩溃行为；该方法因简单易行得以广泛应用，已经作为标准方法纳入了散货船、油船的共同规范体系，指导上述两种船型的极限强度校核.

Smith法在进行逐次崩溃分析时，先将剖面离散成各个单元，在端面施加转角，计算各单元的应变量，由单元应力应变关系可求得相应的应力，再2次积分即可得到相应的弯矩；继续增加转角，就会得到一系列弯矩和转角的关系.将转角除以横框架间距即得到相应的曲率，从而得到船体梁的弯矩-曲率关系曲线[8].具体求解步骤如下.

步骤1将船体剖面离散成各个单元，包括板单元、加筋板单元和硬角单元，其中硬角单元由若干相交的板组成，用来模拟不可能发生屈曲的构件，其应力应变关系通常假设为理想弹塑性模型.

步骤2计算所有单元的平均应力-平均应变关系.

步骤3设定初始曲率和初始中和轴位置，一般取使甲板处应力达到其屈服应力的1%时所对应的曲率为初始曲率.

步骤4根据各单元中心离中和轴的距离确定各个单元的应变.

步骤5按照单元的平均应力-平均应变关系，求得各个单元相应的应力.

步骤6对于每一个增量步，以整个剖面的静力平衡为准则，确定中和轴的位置.

步骤7将各个单元所受的力对中和轴求矩，并将其相加，得到作用在整个剖面的弯矩.

步骤8增大曲率值，转回步骤4，继续求解，得到一系列弯矩-曲率关系曲线，其最大值即为船体梁的极限强度.

2 宽扁型江海直达船体结构极限强度

2.1 宽扁型江海直达船结构特点及主尺度

在江海直达船开发过程中，通过开展经济性分析、适航性能和结构安全性能研究，以装载量大、油耗低、节能环保、安全高效为目标，开发出宽扁型节能环保江海直达集装箱船.采用理论分析、数值计算和模型试验相结合的研究方法，攻克宽扁船型在安全技术、节能技术、绿色技术应用等方面的关键技术问题，以达到安全、降耗和环保的目标.

目标船主尺度见表1.采用双底双壳结构，双层底高1.5 m，双壳宽2.6 m，双壳间设2层平台，分别距基线3.8和6.3 m，典型横剖面见图1.该船的型宽型深比(B/D)达到了2.98，超出了当前中国船级社海船规范规定的B/D不大于2.5的规定.宽扁型船总纵强度偏弱，给合理、安全、可靠的船体结构设计带来了巨大挑战.

表1 宽扁型江海直达船主尺度

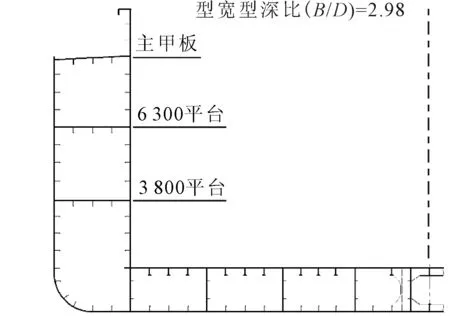
图1 宽扁型江海直达船典型横剖面图

2.2 船体结构逐次崩溃行为

采用基于弹性大变形分析和刚塑性力学分析相结合的半解析方法开发的程序系统“HULLST”用于“4E”级宽扁型江海直达船体结构崩溃行为分析，该程序系统计算分析精度已经在系列对比计算中得以验证[9-10].计算时，采用“双跨”模型，即计算模型包括从强横框架位置出发向前及向后各半个横框架间距，计算模型的前后端面为两强横框架的中间，根据变形特征施加对称的边界条件，强横框架剖面处由于强横框架的作用，根据变形特征在船底限制垂向平动自由度(Uz=0)及纵向转动自由度(θx=0)，在舷侧限制横向平动自由度(Uy=0)及纵向转动自由度(θx=0),见图2.

图2 计算模型及边界条件

在计算模型的前后端面任意位置设主节点m，基于平断面假定，断面上各节点与主节点的横向转动自由度(θy)保持一致，主节点有纵向平动自由度(Um)和横向转动自由度(θm).距主节点距离Zi的节点i，其位移量与主节点位移量的关系为

di=Hidm

(1)

同样，各节点i处的节点力Fi及弯矩Mi可通过下式转换为主节点的等效节点载荷：

Fm=HiTFi

(2)

逐步加大主节点处的转角从而获得相应的弯矩值，得到弯矩-曲率关系曲线.开发的“4E”级宽扁型江海直达船具有双底单甲板结构，因而其中垂弯矩较中拱弯矩要小.中垂状态下船体结构弯矩-曲率关系曲线见图3.

图3 中垂状态船体结构弯矩-曲率关系曲线

不同载荷水平下各构件的应力分布见图4.图4中的实心圆为该构件发生了屈曲，三角形为该构件发生了屈服.在加载初始阶段，弯矩水平不超过1.0×106kN·m时，船体结构各构件均呈弹性状态，应力沿高度方向呈线性分布，见图4a),随着弯矩的增加，各构件的应力也逐渐增大，甲板结构在纵向压缩载荷作用下首先发生屈曲，船体结构总体刚度降低,见图4b)；随着弯矩的进一步增加，甲板结构、6 300平台结构以及6 300平台以上的舷侧结构和内壳结构等先后屈曲，中和轴位置向下移动，船底结构部分构件屈服，从而整体结构丧失承载能力，达到极限强度状态,见图4c)；上部结构屈曲后各构件的应力会重新分配，中和轴位置进一步向下移动，更多舷侧结构和内壳结构发生屈曲，更多船底结构发生屈服，变形增大的同时断面弯矩急剧降低，典型应力分布,见图4d).

图4 中垂状况下不同载荷水平时各构件的应力分布

弯矩的最大值为1.26×106kN·m，此值即为中垂状态下目标船的极限强度.

3 宽扁型江海直达船外载荷计算

江海直达航线涵盖了江段和海段，江段所受波浪载荷很小，海段相对要大得多，因此遭受的波浪载荷具有间歇性，这与传统的内河船或海船波浪载荷有显著的不同.本文研究中先根据船舶航行的航线实际状况来确定波浪载荷的概率水平，随后选取能反映航区特征的波浪谱，根据该航区的波浪散布状况进行波浪载荷长期预报，得到等效设计波高，然后按设计波理论进行外载荷直接计算.具体计算过程参见文献[11].

3.1 外载荷计算模型

外载荷计算时，把船体看作刚体，建立仅外壳的湿表面模型和包括所有构件的质量模型，计算指定波浪条件下沿船体表面的压力分布和相应的船体运动，将运动惯性力也视作外力，与船体表面压力合在一起，成为作用于船体的外载荷.为了最大限度地减少载荷转换误差，载荷计算用外壳模型尽可能与结构计算模型的网格保持一致.

船舶的质量分布决定了浮态，进而影响其所受的外载荷.先把除主机、舱口盖等较大质量的设备之外的空船质量沿船长方向分若干段，通过改变密度的方式分段模拟空船质量分布；主机、舱口盖等重量较大设备按其作用区域以质量点的形式分布到相应位置；货物质量按其作用区域分布到相应构件；油、水的质量通过改变相应油舱或水舱结构密度的方式施加到相应构件.最后，对三维质量模型进行检查以确保其与设计状态一致，尤其是重心纵向位置，如果误差在1%以内，认为与设计状态基本相符，否则需检查误差产生的原因，并进行修正，直到满足要求为止.

3.2 波浪载荷预报

利用SESAM软件中波浪载荷计算模块WADAM，根据航线状况确定的波浪谱、波浪散布图和超越概率，考虑典型装载工况，进行波浪载荷长期预报.相应的波浪特征参数的取值如下： ①波浪频率的范围从0.1～2.0 rad/s，间隔0.1 rad/s，波浪频率数共20个；②浪向角从0°～180°，间隔30°，共7个浪向；③计算航速取为零，水深为无限水深.

对各工况下各种波浪特征参数的波浪载荷进行长期预报，得到各装载工况的波浪载荷长期预报峰值及其对应的浪向、频率等特征参数.满载和压载两种典型装载工况的波浪载荷长期预报峰值、对应的浪向、波浪频率以及单位波高的响应、等效设计波高等特征参数见表2.

表2 波浪载荷预报结果

3.3 外载荷计算

作用于船体的外载荷包括静水载荷和波浪载荷两部分，波浪载荷已在上节中进行了计算分析，静水载荷是由重力和浮力的差值引起，各装载工况下重力分布会有所不同，从而静水载荷也会不同.各装载工况下静水载荷的包络线即为设计许用静水载荷，将其与波浪载荷一起成为船体外载荷.

中拱状态下最大许用静水弯矩为2.200×108N·m，中垂状态下最大许用静水弯矩为-1.152×108N·m，故中拱状态下最大外载荷为6.950×108N·m，中垂状态下最大外载荷为-5.902×108N·m.

4 宽扁型江海直达船体结构安全裕度

船体结构极限承载能力和所遭受最大外载荷是船体结构安全可靠的两个重要方面，二者的比值即为船体结构安全系数，代表着船体结构的安全裕度.明确船体结构的安全裕度，方能确切把握船体结构能抵抗极限海况的能力，或是在设计载荷下进行结构轻量化设计，在安全可靠前提下，探寻轻量化船体结构设计方案.

船体结构中拱和中垂状态下的弯矩-曲率关系曲线及最大外载荷见图5，弯矩-曲率关系曲线的最大值即为船体结构极限承载能力.中拱状态和中垂状态下船体结构极限承载能力、所遭受的最大外载荷及安全系数等总结见表3.中拱状态下结构安全系数为1.942，中垂状态下结构安全系数为2.135，说明目标船在设计载荷下可保持安全状态，结构极限承载能力大约是最大外载荷的两倍.

图5 中拱和中垂状态下船体结构弯矩-曲率曲线

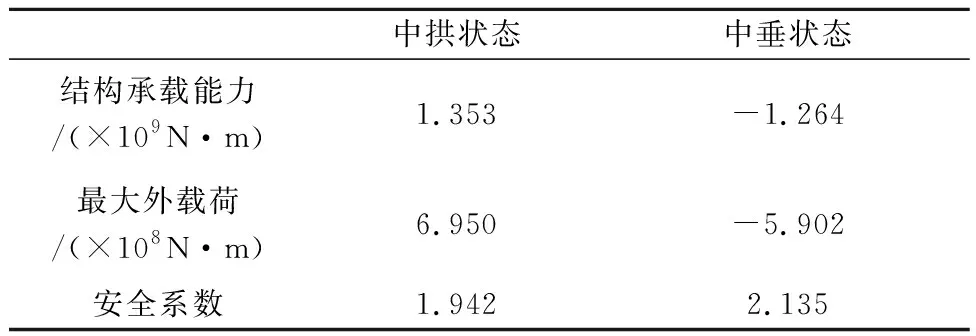
中拱状态中垂状态结构承载能力/(×109N·m)1.353-1.264最大外载荷/(×108N·m)6.950-5.902安全系数1.9422.135

5 结 束 语

长江由于天然航道的制约，船舶大型化唯有向船宽方向发展，研发宽扁肥大型船舶，本文以开发的武汉-宁波舟山航线“4E”级江海直达船舶为研究对象，该船宽深比达2.98，基于弹性大变形分析和刚塑性力学分析相结合的半解析方法获得单元的平均应力-平均应变关系，采用Smith方法对该船进行逐次崩溃分析，获得船体结构极限承载能力.随后根据航线实际状况来确定波浪载荷的概率水平，选定能反映航区特征的波浪谱，根据波浪散布状况进行波浪载荷长期预报，按设计波理论进行外载荷直接计算以得到作用于船体的最大外载荷.

通过对“4E”级宽扁型江海直达船的船体结构极限强度和最大外载荷两方面的计算分析，明确船体结构的耐力和所受到的外力，把握船体结构的安全裕度和抗极限海况的能力，为今后理性、合理、安全、可靠的船体结构最优化设计奠定基础.

参考文献

[1] 中国内河水运市场现状调研与发展前景分析报告(2018-2025年)[R/EB].中国产业调研网，2017.http:∥www.cir.cn/R-JiaoTong Yun shu/85/NeiHeShui Yun DeFa ZhanQiao Jing.html.

[2] 柴俊凯.江海直达船极限强度研究及结构优化[D].武汉：武汉理工大学,2012.

[3] 傅何琪.江海直达运输船极限强度研究[D].武汉：武汉理工大学,2013.

[4] NILVA V A,UKRAINE. Analytic method of definition of geometric characteristics of inland or river-sea navigation dry-cargo vessel after receiving damage[C]. The Asian-Pacific Technical Exchange and Advisory Meeting on Marine Structures，2015.

[5] NILVA V. A Residual strength assessment for mixed river-sea going dry going dry cargo vessel when part of longitudinal members are missed[J].Visnyk ONMU,2013,39:96-108.

[6] KHEDMATI M R, RASHEDI A R. Nonlinear finite element modelling and progressive collapse analysis of a product carrier under longitudinal bending [J]. Applied Ocean Research, 2014,48:80-102.

[7] PEI Z，FUJIKUBO M. Application of idealized structural unit method to progressive collapse analysis of a ship’s hull girder under longitudinal bending [C]. Proc of 15th Int. Offshore and Polar Engineering Conf, Montreal，2005.

[8] SMITH C S. Influence of local compressive failure on ultimate longitudinal strength of a ship’s hull [C]. PRADS,Tokyo,1977.

[9] YAO T, NIKOLOV P. Progressive collapse analysis of ship′s hull girder under longitudinal bending [J] Soc. Naval Architects of Japan, 1991,170:449-461.

[10] YAO T, ASTRUP O C, CARIDIS P, et al. Report of special task committee vi.2:“ultimate hull girder strength” [C]. Proc. 14th ISSC,Nagasaki, 2000.

[11] 姜伟，裴志勇，吴卫国.宽扁肥大型江海直达船结构强度探析[J].中国水运，2017(1):54-57.