基于CosmosWorks的换热器封头静强度分析
2018-07-04李恺锋王子坤
李恺锋, 王子坤
(贵州永红换热冷却技术有限公司, 贵州 黔南州 550600)
引言
静强度是属于结构静力学的设计问题,主要关注工程上结构元件材料本身的最大承载力。主要考虑结构元件上局部点的工作应力是否存在大于材料本身的强度极限的危险。
COSMOS/Works是SRAC公司推出的一套有限元分析软件(COSMOSsWorks)下面的一个模块,它采用世界上最快的有限元分析法——快速有限元算法(FFE)将高高在上的有限元分析平民化,普通工程师可以进行工程分析并较快得到结果[1]。
板翅式换热器是一种重要的机械设备。在冷却器设计时,必须满足性能要求、工艺要求、可靠性要求和经济性要求。以往在使用COSMOS来模拟槽板的强度是否满足设计要求时都用设计压力去进行模拟,保证产品结构安全。由于电脑设备的限制(网格划分的限制)实际上得到的安全系数一般较高,这样产品生产的材料消耗大、经济性不好。本文通过理论计算和模拟分析相结合,依据试验数据给出了安全系数的参考要求[2]。
1 强度理论
构件受外力作用后,构件内部存在应力、应变,同时积聚了应变能,归纳构件失效的情况,发现构件基本的失效形式有两种:屈服和断裂。基于构件强度失效的不同决定因素,有四大假设理论解释,也就是四大强度理论。
1.1 脆性断裂
1)第一强度理论(最大拉应力准则)。
无论材料处于什么应力状态,只要发生脆性断裂,其共同原因都是由于微元内的最大拉应力σ1达到了材料的强度极限[σ]。
依据第一强度理论建立的强度条件:σ1≤[σ]=其中n为安全系数。
2)第二强度理论(最大拉应变准则)。
无论材料处于什么应力状态,只要发生脆性断裂,其共同原因都是由于微元内的最大拉应变ε1达到了材料的强度极限εf。
在单向拉伸下,用胡克定律计算拉应变的极限值为
根据广义胡克定律危险点出最大拉应变有ε1=
根据定义可以建立强度条件:σ1-μ(σ2+σ3)≤σ=
1.2 塑性断裂
1)第三强度理论(最大切应力准则)。
无论材料处于什么应力状态,只要发生屈服或剪断,其共同原因都是由于微元内的最大切应力τmax达到了构件在单向拉伸下发生塑性屈服时极限切应力 τs。
根据定义可以建立强度条件τs,可以得出
2)第四强度理论(均方根切应力准则)。
无论材料处于什么应力状态,只要发生屈服或剪断,其共同原因都是由于微元内的形状改变比能uf达到了材料在单向拉伸下发生塑性屈服时形状改变比能ud[3]。
根据定义可以建立强度条件可以得出
2 COSMOS静强度模拟分析和计算比较
以某换热器封头为例。取组件长度为150 mm,在1 MPa的爆破压力(爆破压力为设计压力的5倍)下模拟槽板的强度是否满足要求。
由于铝合金属于塑性材料,根据第四强度理论可以确定此槽板的安全系数。
网格划分时注意各拐点处的网格分布,如图1。

图1 网格划分
COSMOS上的设定:结果选项处添加安全系数图解。选择最大vonMises应力。在定义材料后系统会默认使用第四强度理论,如图2。

图2 模拟结果
设定应力极限到屈服力。此时就可以参看结构的安全系数。n1=0.87<1.5。
同时,可以在应力结果中查看三个主应力的情况 σ1、σ2、σ3(在 COSMOS 中表示为 P1、P2、P3):σ1=182×106N/m2,σ2=102×106N/m2,σ3=43×106N/m2。
和σvonMises应力的最大值σvonMises=142 MPa。
将产品爆破看成是某一点的形状改变比能超过了材料发生塑性屈服时形状改变比能,显而易见这个点就是σvonMises应力最大的点,所以直接用这个σvonMises应力计算安全系数
这里将三个主应力放在一个点上,做一个简单的估算:
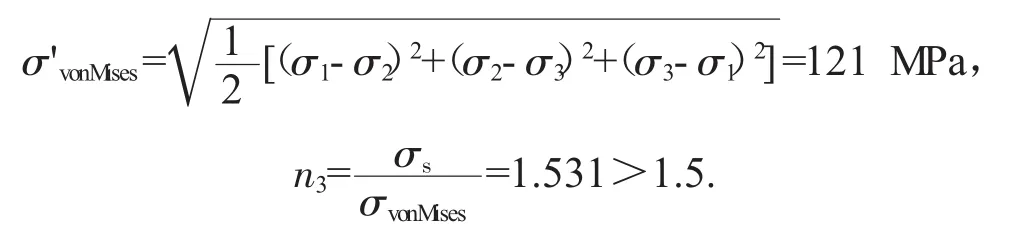
结果发现计算出的安全系数n2和n3都要比COSMOS模拟的安全系数n1要大。
这是因为有限元的计算方式导致:1)COSMOS/Works认为材料是线性的,也就是应力与应变成正比。这就指出了在整个模型变形的过程中,模型的刚度为一恒定值(材料未变形的刚度值)。实际上根据材料力学性能分析可以知道:刚度在材料变形后会不断发生变化。FEA基本方程中刚度矩阵[K]若用非线性适量迭代计算可以有效减少误差。2)所有载荷被缓慢且逐渐应用,直到它们达到完全量值。在达到完全量值后,载荷保持恒定(不再随时间变化)。这样载荷产生的加速度和速度就很小,可忽略不计,因此此假设就忽略了惯性和阻尼力。3)有限元计算式各各网格的值不断迭代计算,这样如果有一个值有误差,结果会越来越偏离。如果将网格优化,在可能的危险点处网格细化(网格控制),可以将误差减少一部分(能量范数误差可以在应力结果中查看),但仍然满足,n2>n1如图 3。
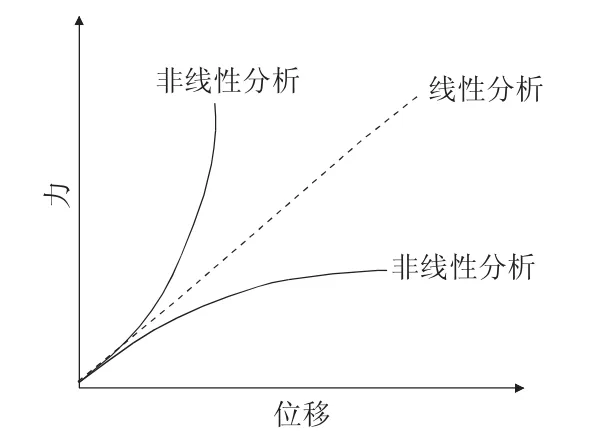
图3 应力与应变的关系
n3是对安全系数的估算,假设一个点(单位微元)上三个主应力全是最大的(也就是材料失效点),直接计算得出的结果。实际上这三个主应力(σ1、σ2、σ3)最大的点不是在一个危险点,而常用的危险点是指σ1最大的(第一强度理论)。也就是说计算点的σ'vonMises应力比实际上槽板结构的应力σvonMises要大得多。理论上槽板实际安全系数还要比n3大。
工程中一般认为安全系数在1.5~3时产品满足强度要求。所以此槽板在1 MPa的压力下COSMOS给出的安全系数为0.87,但这是满足强度要求的(结果与爆破实验结果相符合)。
3 结论
本文通过计算、模拟对比的方法,发现了COS-MOS模拟的安全系数与实际安全系数不符合。COSMOS模拟的值不可直接用来作为设计依据,COSMOS的模拟安全系数太过于保守。根据产品的爆破试验,将合格槽板结构的最大爆破值代入COSMOS模拟,发现在能量范数误差300左右的情况下,安全系数为0.4~0.8之间。所以在槽板设计过程或是在材料减薄项目中可以使用产品的爆破压力对结构进行分析,只要保证最大合应力下(第四强度理论)安全系数≥0.5就可以认为产品是合格的。
[1]廖景娱,刘正义.金属构件失效分析[M].北京:化学工业出版社,2003.
[2]范钦珊,殷雅俊.材料力学[M].北京:清华大学出版社,2004.
[3]成凤文.压力容器三维建模及应力分析[M].北京:工程图学学报,2006.
