基于ANSYS的车载加固显示器振动试验夹具设计

李 婷，张 宇，杨 娇

（国营第785厂第三研究所， 山西 太原 030024）

引言

作为特殊的电子产品，车载加固显示器长期置于恶劣的环境条件下，这意味着振动环境对车载加固显示器可靠性的影响非常重要。振动试验夹具用于安装固定车载加固显示器，模拟其在实际工作状态下传递振动的特性，试验夹具设计的好坏极大地影响了振动结果。选用理想的振动试验夹具可以实现对车载加固显示器的不失真传递作用，从而使产品更好地适应严格的振动指标。

1 车载加固显示器振动试验夹具有限元模型的建立

以LDS V984振动系统为基础，设计L型结构的车载加固显示器振动试验夹具，其整体尺寸设计为800 mm×800 mm×1 900 mm，选用铝合金材质。与振动系统间采用螺栓固定，并预留沉头连接孔。两侧和后板均采用加强筋均布来加大夹具的固有频率。

振动试验夹具的实体模型是通过三维建模软件Solid Edge V20来实现各种特征的创建。网格划分质量的好坏极大程度上决定着有限元分析结果的精确程度，故网格大小的选择有着至关重要的作用[1]。本文选用四面体单元对振动试验夹具进行网格划分，得到有限元模型见图1，共计119 646个节点数，67 474个网格数。

2 随机振动响应分析与求解

在振动下极易引起设备内部结构的动态位移，加剧结构的疲劳和磨损。随机振动作为一种非确定性振动，无法用准确的函数来说明，就某范围而言，其可借助功率谱密度（PSD）来确定。随机振动试验的目的在于验证设备是否能承受寿命周期内的振动与其他叠加条件下正常工作[2]。基于有限元技术，进行试验夹具的随机振动分析，来验证其是否满足振动要求，以完善制造完整性和系统可靠性。

2.1 随机振动理论基础

响应的功率谱密度函数矩阵：

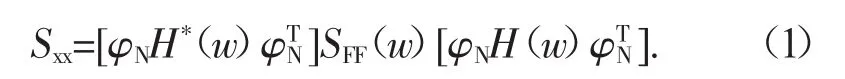
式中：φN为系统的简正模态矩阵，H（w）代表关于正则坐标的复频响应矩阵，H*（w）是其共轭阵。

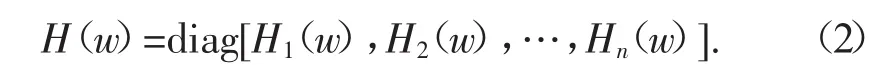
通过公式（2）可借助已知激励的功率谱矩阵SFF（w）计算出响应的功率谱矩阵Sxx（w）。将SFF（w）进行傅里叶逆变换，即获得响应的相关函数矩阵[3]：

2.2 模态分析

在进行随机振动分析之前，需进行模态分析。将振动试验夹具的底部螺栓连接面采用全固定约束，求解得到振动试验夹具的前十阶固有频率，如下页表1所示，前2阶模态振型如下页图2所示。

表1 振动试验夹具的前十阶固有频率

图2 前2阶模态振型

2.3 随机振动响应分析

车载加固显示器振动试验夹具振动谱型参考《GJB150.16A-2009》军用装备实验室振动试验部分高速公路卡车振动环境荷载谱参数，其拐点汇总如表2所示。

为保证足够的计算精度，先求解的模态数对应的频率应大于激励的频率。由表1可知，最高阶频率为600.48 Hz，大于500 Hz，说明振动试验夹具前十阶模态分析可满足计算精度。

选择PSDG Acceleration，将表2所示纵向、横向和垂向三个方向的PSD谱激励分别加载到车载加固显示器振动试验夹具上。载荷设置完成后，提取等效应力结果图。ANSYS软件默认提取的是一个“Sigma”概率对应的值，为了实现广泛性，本次分析以“3Sigma”概率结果查看，结果如图3所示。

通过分析结果可知：车载加固显示器振动试验夹具在最大应力点处有不超过99.737%的概率形成9.961 4 Max应力，这对于一般的铝合金结构而言，此应力值较为安全，可满足试验振动夹具要求。

3 结语

设计L型结构的车载加固显示器振动试验夹具,并采用加强筋均布于两侧和后板的形式，在有效控制振动试验夹具重量的同时，较好地加大了固有频率。借助有限元法进行振动试验夹具随机振动的响应分析，验证了模型的合理性，节约了设计成本。该方法对其他类似电子设备的设计也具有很好的指导和参照意义。

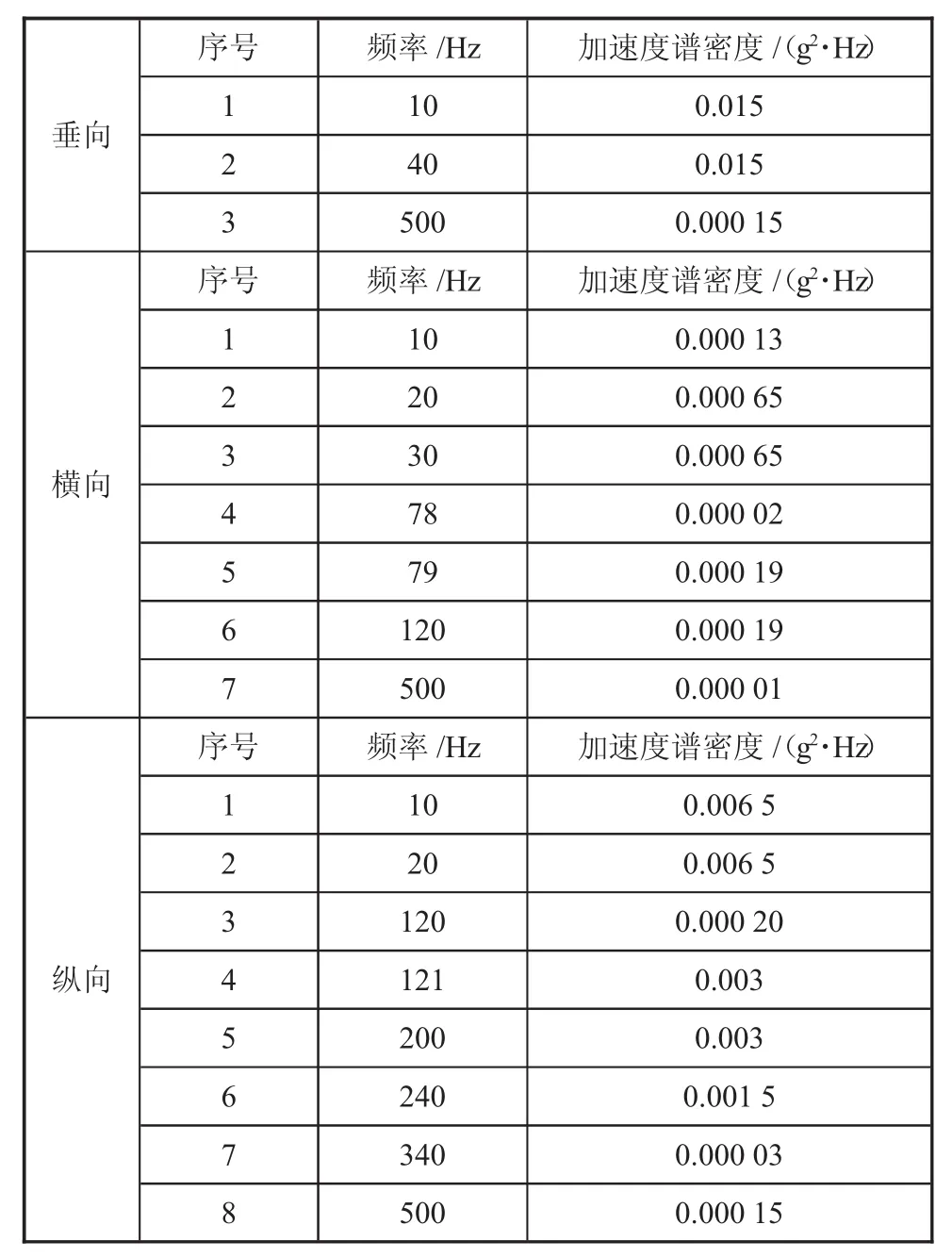
表2 高速公路卡车振动环境荷载谱参数

图3 等效应力云图

[1]魏新利，付卫东，张军.泵与风机节能技术[M].北京：化学工业出版社，2010.

[2]刘天笑，蒋超奇，蒋丙云，等.ANSYS Workbench有限元分析工程实例详解[M].北京：中国铁道出版社，2017.

[3]庄表中，梁以德，张佑启.结构随机振动[M].北京：国防工业出版社，1995.