基于传播影响力的重叠社区划分算法

谭文安,陈雅雯,潘义博

(1.上海第二工业大学 计算机与信息工程学院,上海201209;2.南京航空航天大学 计算机科学与技术学院,南京211106)

0 引言

随着信息技术的迅速发展,复杂网络研究逐渐成为学术界的热点。社区结构与小世界性、无标度性并列,是复杂网络最重要的特性之一,同一社区内部节点之间联系密切,不同社区之间的节点联系稀疏[1]。

目前已有的社区发现算法根据划分所得的社区是否存在重叠节点,可分为重叠社区和非重叠社区。早期的研究多为非重叠社区发现,即将完整的网络拆分成若干个互不相交的子网,较经典的有FN算法(Fast-Newman Algorithm)[2]、GN算法(Girvan-Newman Algorithm)[3]和LPA(Label Propagation Algorithm)算法[4]等。之后涌现了许多经典算法的改进算法,Jin等[4]采用结构相似度取代了GN算法中边介数的概念,从而有效降低了算法的时间复杂度;Zhang等[6]与Peng等[7]分别针对LPA算法的缺陷进行了改进。

随着对复杂网络的深入研究,人们发现大多数真实网络中的节点与社区之间可能并不是简单的“非此即彼”关系,对重叠社区的研究更具有现实意义。为此,Palla等[8]提出了CPM(Clique Percolation Method)算法,该算法通过搜索邻接团来挖掘重叠社区。Gregory等[9]提出COPRA算法(Community Overlap PRopagation Algorithm),对传统LPA算法进行修改,使之适用于重叠社区发现。Lancichinetti等[10]提出LFM算法(Local Fitness Method),该算法通过局部扩展的方法进行重叠社区发现。Shen等[11]提出了基于极大团的凝聚式层次聚类方法,将极大团视为社区的基本单元,用于发现网络中的重叠社区结构。Meghanathan等[12]提出了基于邻域重叠的贪婪社区挖掘算法,以邻域重叠度的递增顺序依次迭代删除网络的边,并以模块度值为算法优化目标。

加权网络中的社区发现研究成果相对较少。Blonel等[13]基于加权复杂网络的模块度提出了十分经典的Louvain算法,实现在较大规模的复杂网络上的社区发现。Bai等[14]提出利用成员向量来分配节点所属社区,实现基于密度峰值的社区发现算法。杨贵等[15]根据节点权重选取种子节点,并根据节点对子图的适应度函数将种子节点扩展成局部稠密子图,最后合并局部稠密子图实现社区划分。

上述算法大多只能应用于无权网络,现实生活中,网络中的边并非完全是存在与否的布尔关系。因此,加权网络相比无权网络更具有现实意义。针对加权网络中的重叠社区划分问题,本文提出了一种基于传播影响力的重叠社区划分算法COPRA-PI,该算法能够高效地挖掘加权网络中的重叠社区。

1 理论基础与技术

1.1 相关算法介绍

1.1.1 LPA算法

2007年,Raghavan等[4]提出LPA算法。该算法基于相似的节点应属于同一个社区的思想,其主要过程如下:①初始化过程,为每个节点赋予一个与节点编号相同的标签;②迭代过程,将标签更新为与大多数邻节点相同,若出现频率最高的标签不止一个,则随机选取其中一个来更新自己的标签;③重复第②步,直到整个网络中的标签达到稳定的状态;④将标签相同的节点归为一个社区。

LPA算法的优点是时间复杂度低,其缺点也很明显:迭代过程中随机选取新标签会导致算法结果不稳定。传统标签传播算法采用异步更新策略,即一部分节点在第t次迭代时及时更新自身所携带的标签,剩余节点在第t次迭代后不立即更新自身的标签。每次迭代时随机选择本次需要及时更新的节点。刘世超等[16]通过实验证明同步更新策略比异步更新策略划分结果更稳定、准确。

1.1.2 COPRA算法

2010年,Gregory等[9]基于LPA的重叠社区发现算法提出了COPRA算法。当社区允许出现重叠时,一个节点就可能出现在两个不同的社区中,为此Gregory设计了一种标签对集合的形式来表示节点所属社区。标签对(c,b)中的c是标签号,b是节点与社区c的隶属度或符合度。该算法还设置了一个最大标签数m,即节点最多只能属于m个社区。迭代次数为t时,节点x与社区c的隶属度可用下式计算:

其中,N(v)表示节点v邻居节点的集合。

算法主要过程如下:

(1)社区初始化。将每个节点v的标签cv赋值,值与节点编号相同,将节点v与标签cv的隶属度设置为1,即(cv,1)。

(2)迭代过程。每个节点v通过式(1)计算自身与邻居节点携带的社区标签的隶属度。保留隶属度大于1/m的标签,加入标签对集合。如果所有的标签对中的隶属度都小于1/m,则选择其中隶属度最大的标签加入标签对集合。当隶属度最大的标签对不止一个时,从其中随机选择一个加入标签对集合。确定节点的标签对集合后,对隶属度进行规范化表示,使其满足

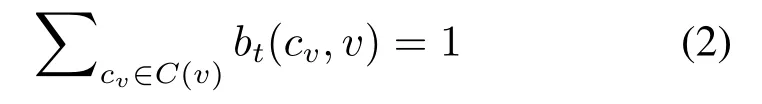
式中,c(v)表示节点v可能属于的社区标签的集合。

(3)重复步骤②,直到算法终止条件(跟踪每轮计算结束后网络中剩余标签集合的大小,当连续两轮不变,则认为满足终止条件)。

(4)每个节点所带的标签对中的标签即代表节点所属的社区,节点的标签对集合中有几个标签对即代表节点属于几个社区。

COPRA算法的优、缺点和LPA算法相似。算法在执行过程中稳定性较差,主要表现在以下方面:m值需要手动设置,具体选取方式不确定;算法执行过程中对标签的随机选取操作会造成结果不稳定。

1.1.3 LFM算法

Lancichinetti等[10]提出LFM算法。该算法利用网络的局部特性,从单独的节点开始直至扩展成一个社区。算法主要过程如下:

(1)随机选取一个节点作为社区G的初始成员;

(2)选择社区G所有邻居节点中贡献最大的节点加入社区G;

(3)计算并过滤社区G中贡献值为负数的节点;

(4)重复第②步和第③步,直至社区G所有邻居节点对其的贡献值都为负数;

(5)若网络中还存在未划分的节点,则在其中随机选取一个节点作为新社区G′的初始成员,返回第(2)步,否则结束。

算法中提出了社区的适应度函数:

式中:是社区G内部边的数量;是社区G与社区外节点连边的数量;参数α控制社区数量,取值为0～2之间的整数。

节点对社区的贡献函数为

式中:fG+v是节点v加入社区G后社区的适应度;fG−v是节点v未加入时社区的适应度。

LFM算法的优点是算法过程易理解,但算法随机选取的种子节点的优劣程度直接影响着后续的划分结果,导致其鲁棒性较差。

1.2 社区划分的评价指标

Newman等[17]提出了一种衡量社区划分质量的评价标准,称为模块度函数。模块度函数定义为

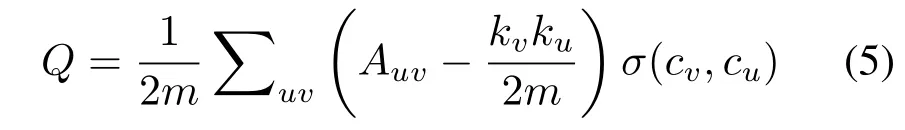
式中:Auv为网络邻接矩阵中的元素,定义为,如果节点u和v相邻,Auv为1,否则为0;kv表示点v的度;m为网络中边的总数。如果v和u在一个社区,函数σ(cv,cu)的取值为1,否则为0。

分析上述模块度函数公式可知,Q的数值越大说明划分的社区质量越好。但是,当社区之间存在重叠节点的情况下,该模块度公式将不再适用。学者们在重叠社区发现的研究过程中对衡量指标进行了改进,如乔少杰等[18]提出引入节点的模糊隶属函数来表示节点属于不同社区的“程度”;Shen等[11]对模块度函数Q进行改进,把模块度函数扩展到具有重叠社区结构的网络中,并且证明了重新定义的模块度数值越高表示重叠社区划分的效果越好,模块度函数被重新定义为

式中,Ov表示点v所属的社区个数。分析式(5)与式(6)可以看出,如果社区之间不存在重叠,那么表达式Q与表达式EQ是完全等价的。

2 基于传播影响力的重叠社区划分算法COPRA-PI

2.1 概念定义

加权网络是由一组节点和其带权值的边所组成的全连通网络,其中网络中节点个数为m,边的数量为n。下面是关于基于传播影响力的重叠社区划分算法(COPRA-PI)的概念定义。

定义1(边权值) 节点i与节点j之间的边权值用Aij表示,若Aij=0则表示i与j之间不存在连边。

定义2(节点的度) 或称节点强度,是连接该节点全部边的权重之和,节点i的度用Di表示,可由下式计算:

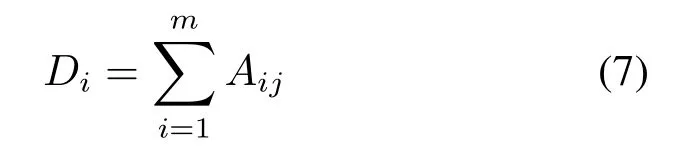
定义3(节点影响力) 指的是标签在传播的过程中,传播者对接受者的影响。用V Ii→j表示标签从节点i传播到节点j时的节点影响力,计算式为

定义4(边影响力) 指标签在传播过程中所经过的边对传播过程的影响。用EIi→j表示节点i与节点j之间连边的边影响力值,其公式为

定义5(历史标签影响力) 指节点的历史标签对新标签的影响。历史标签影响力HIi衡量节点i的历史标签对当前更新策略的影响,采用下式计算HIi:

式中:Ei为与节点i相连的边的数量;Di/Ei表示节点i的平均度,因此可以把历史标签影响力看作是一个跟节点i相同度数的节点通过一条权值为Di/Ei的边对节点i进行标签传播的影响。

定义6(标签概率矩阵) 指每个节点拥有每个标签(属于某个社区)的概率大小,用一个m×m的矩阵P来表示,其中Pij表示节点i拥有标签j(节点i属于社区j)的概率大小。最终每个节点所拥有的标签的概率和应为1,即

定义7(节点最大标签数) 指节点能拥有的最大标签个数。可用下式(12)计算节点i的最大标签数,

式中:CLi为节点i当前的候选标签数量;Ei为节点i的边的数量。

定义8(标签过滤)由于有最大标签数量L max的限制,因此需要对标签概率矩阵中的标签进行过滤操作,当标签概率小于1/(L max)时,表明该标签与节点之间匹配程度不高,不足以保留。实际操作中,标签过滤操作指的是将标签概率小于1/(L max)的标签的概率值置为0。

定义9(标准化) 每轮标签传播迭代结束后,都需要对标签概率矩阵进行标准化操作,使其符合的要求。采用式(13)对标签概率矩阵进行标准化处理。

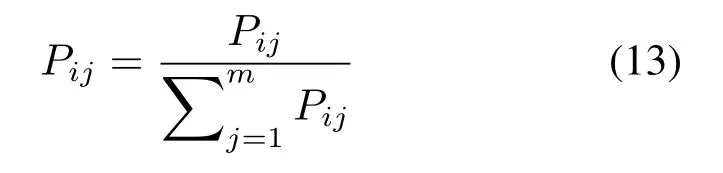
2.2 算法描述

2.2.1 算法流程

基于传统标签传播算法中节点应与其大多数邻居属于同一社区这一思想,本文提出COPRA-PI算法,来解决复杂网络中的重叠社区发现问题。该算法在经典重叠社区发现算法COPRA的基础上进行了以下改进。

(1)将边的权值与节点的度结合,采用节点强度的概念代替节点的度。在标签传播过程中,即使是直接相邻的节点也有“亲疏”之分,这种“亲疏”之分来源于节点之间连边的权值不等,因此计算新标签时应该将边影响力因素也考虑进去。

(2)影响节点迭代后所属社区的不应该只有节点邻居的影响力与加权边的影响力,节点自身的历史标签信息也应作为节点下一轮所属社区的影响因素。针对上述分析的3个影响因素,COPRA-PI算法综合考虑历史标签遗留的影响力、边影响力和节点影响力对节点新标签的影响。

(3)现有研究中,节点每次迭代可容纳的标签数是固定的,并且需要人为设置,然而实际各个节点可容纳的标签数量应与节点本身以及当前候选标签情况相关,同时人为设置节点的最大标签数需要较多的先验知识。针对这一问题,COPRA-PI算法采用动态确定节点最大标签数的方法,更具有合理性。

算法流程如图1所示。

图1 COPRA-PI算法流程图Fig.1 COPRA-PI algorithm f l ow chart

2.2.2 算法主要步骤

(1)社区初始化。每个节点初始化时只携带一个与自身编号相同的标签,将标签概率矩阵置为一个单位矩阵。

(2)标签传播。传播过程中新的标签概率由节点影响力、边影响力和历史标签影响力这3个因素共同决定。传播后新的标签概率采用下式计算:

式中:表示第t轮迭代时节点i属于社区j的概率;HIi表示历史标签影响力;表示第t−1轮迭代时节点i属于社区j的概率;s表示节点i邻居节点的个数;vk表示节点i的第k个邻居节点;V Ivk→i表示标签从vk传播到节点i的节点影响力;E表示连接节点vk与节点i的边影响力;表示第t−1轮迭代时节点vk属于社区j的概率。

(3)标准化概率矩阵与标签过滤。在每轮标签传播结束以后,由于可能无法保证标签概率矩阵中各个节点所携带的标签的概率之和为1和最大标签数量L_max的限制,因此需要对节点进行标签过滤以及标签概率矩阵标准化的过程。过滤与标准化时采用以下原则:如果节点的最大标签数量为1,则直接选择概率最大的标签,将其概率置为1,同时将其余标签的概率置为0;否则,采用式(13)对标签概率矩阵进行标准化,然后对节点的标签进行过滤操作,最后再用式(13)重新进行标准化。

(4)整个网络中的标签达到稳定的状态,不再随着标签传播而变化或者已经达到了给定的最大迭代次数则算法终止,否则重复步骤(2)～(4)直到满足算法终止条件。

2.2.3 算法伪代码

算法1COPRA-PI算法

输入 网络的邻接矩阵A,节点个数m,边的个数

n,最大迭代次数max-C

输出 标签概率矩阵P

1.for i from 1 to m do

2.for j from 1 to m do

3. Di=Di+Aij

4.end for

5.end for

6.for i from 1 to m do

7.Pii=1

8.end for

9.count=0

10.do

11.for i from 1 to m do

12. 根据式(14)计算新的标签概率new_Pi

13.end for

14.根据式(13)对标签概率矩阵new_P标准化

15.调用new-P=LF(new-P,A,m)进行标签过滤然后对new-P标准化

16.count=count+1;

17.P=new-P

18.until每个节点的标签都稳定或者count≥max-C

说明:第1～4步计算网络中每个节点的强度,将边的权值信息融入节点中。随后在第6～8步将标签概率矩阵初始化为单位矩阵,即将每个节点只拥有与自身编号相同的一个标签。第11～13步计算得到新的标签概率矩阵,第12～16步进行标签的标准化与过滤操作,其中第15步LF调用算法2实现。重复执行第10～18步的操作直到每个节点的标签都稳定或者算法已经达到了给定的最大迭代次数。最后输出最终的标签概率矩阵。其中标签过滤的伪代码实现如算法2所示。

算法2 标签过滤过程

输入 标签概率矩阵P,网络的邻接矩阵A,节点个数m

输出 标签概率矩阵P

1.for i from 1 to m do

2.根据式(12)计算最大标签数L-maxi

3.if L-maxi=1 then

4. 找出节点i的标签中概率最大的标签label

5. for j from 1 to m do

6. Pi,j=0

7. end for

8. Pi,label=1

9.else

10. for j from 1 to m do

11. if Pi,j∗L-maxi＜1 then

12. Pi,j=0

13. end if

14. end for

15.end if

16.end for

2.2.4 算法时间复杂度分析

CORPA-PI算法中计算节点强度的时间复杂度为O(m2),初始化标签概率矩阵的时间复杂度O(m),一次完整传播过程的时间复杂度为O(n·L max),其中Lmax是节点的最大标签数,标签概率矩阵标准化与标签过滤过程的时间复杂度都为O(m2),由于Lmax一般都较小,因此算法时间复杂度为O((c+1)·m2),其中c是迭代次数。

3 实验与结果分析

采用真实数据集进行实验,并与典型的重叠社区发现算法进行对比,从社区发现质量、算法收敛速度等角度验证COPRA-PI算法的效果,并对加权网络与无权网络的划分效果进行对比。实验环境为:1.70 GHz的Intel(R)Core(TM)i5-3317U CPU,4GB内存,Windows 7操作系统,所有算法均采用Java语言实现。

3.1 数据集介绍

实验采用了1组加权数据集和3组无权数据集,其中空手道俱乐部数据集有加权和无权两种形式,除此之外还采用了经典的海豚数据集和美国政治书数据集。下面先介绍数据集的来源与构成。

(1)海豚数据集(Dolphins)。海豚数据集是由动物学家Lussean等人对新西兰神奇峡湾中62只宽吻海豚历时7年多的细致观察后建立的。在观察过程中,他们发现由于其中一只海豚成员的消失,导致这群海豚逐渐分为了2个小群体。海豚数据集共包含62个节点,159条边。

(2)空手道数据集(Karate&Karate∗)。空手道俱乐部数据集是Zachary通过对美国一所大学中的空手道俱乐部成员历时两年的观察而构建的。通过统计一个月内两个成员之间的交流次数形成边的权值。在Zachary观察期间,俱乐部的两位核心成员的意见产生了分歧,导致该俱乐部最终分裂成以这两位成员为核心节点的两个新俱乐部。空手道数据集共有34个节点,78条边,其中Karate*为加权数据集。

(3)美国政治书数据集(Polbooks)。美国政治书网络数据集是由Krebs建立的,网络中的节点代表亚马逊网上书店卖出的有关美国政治的书籍,网络中的边将购买者经常一起购买的书连接起来。以亚马逊网上书店中的图书主题内容与读者评价为依据,上述书籍被分为:自由派、中间派和保守派。该网络包含105个结点和441条边。

3.2 算法效果对比

CMP、COPRA和LFM算法都是重叠社区发现的经典算法。CPM算法的效果一定程度上依赖于社区规模,即k值的大小。k值合适时,划分结果比较理想,反之k值选择不合适时,效果较差。除此之外,该算法在边密集的网络中更适用。基于以上两种局限性,因此本文不选择其作为对比算法。本文选择COPRA算法和LFM算法进行对比实验,但是LFM算法的社区划分结果受初始种子节点质量的影响,种子节点的优劣会影响划分结果,因此对LFM算法进行100次实验取均值。

使用上述4个数集对COPRA-PI算法的效果进行验证。由于真实数据集的划分形式无法确定,因此实验采用由Shen等[11]提出的重叠社区模块度扩展函数EQ来评价网络中重叠型社区发现的质量。表1给出了用不同算法在4个真实网络中划分所得社区的EQ值,其中COPRA算法的最大标签数k需手动设置,当k取值不同时,所得的划分结果也不相同,对比实验取EQ最优时的k值。

表1 COPRA-PI算法与LFM、COPRA对比Tab.1 COPRA-PI Algorithm vs.LFM,COPRA

从表1中可以看出,所提出的COPRA-PI算法的EQ值都高于其他两个算法,这表明所提出的COPRA-PI算法所划分的社区质量更高。分析表中Karate和Karate*的EQ值,可以看出3个算法在Karate*数据集上的模块度值都高于Karate数据集,由此也印证了边权重可以体现节点与节点之间的联系强度,在社区发现的时候考虑权值信息可以取得更加合理和科学的结果。此外,LFM算法在无权网络数据集上的划分结果质量一直不如COPRA算法,但是在加权网络中却取得了远比COPRA算法要好的效果,这表明LFM算法与COPRA算法相比可能更加适用于加权网络数据集中。

为了分析所提出的COPRA-PI算法的划分速度,实验研究了COPRA-PI算法在4个数据集上的收敛情况,实验结果如图2所示。从图中可以看出,COPRA-PI算法的收敛速度较快,在4个真实数据集上均是在10次迭代内就已经达到收敛状态了,结合表1的实验结果可以看出,COPRA-PI算法可以较快收敛并划分出较高质量的社区。

为了研究社会网络图中边权值对社区划分的影响,针对无权Karate和加权Karate∗的社区划分结果进行重点分析。图3和图4分别为COPRAPI算法划分无权Karate和加权Karate∗社区结构得到的。

图2 算法COPRA-PI收敛性图Fig.2 The convergence property of the algorithm COPRA-PI

图3 COPRA-PI算法划分Karate结果图Fig.3 The result diagram of COPRA-PI algorithm by dividing the Karate community

图4 COPRA-PI算法划分Karate∗结果图Fig.4 The result diagram of COPRA-PI algorithm by dividing the Karate∗community

分析图3可知,COPRA-PI算法将无权Karate分成成了两个社区,分别用圆和正方形标记以示区分。其中3号、9号和20号节点表示重叠节点。直观可见,圆标记的社区以34号节点为核心成员,正方形标记的社区以1号节点为核心成员,社区个数及具有明显核心成员这一信息数据集介绍中已知的信息相符合,3个重叠节点可视为这场分裂事件的“中立人员”。重叠节点中的9号和20号节点分别都与两个小团体的核心成员有联系,因此被划分为重叠节点是合理的。重叠节点中的3号节点与两个社区中的成员联系都很密切,且与“中立人员”9号也有联系,所以3号节点被划分为重叠节点也是合理的。

分析图4可知,COPRA-PI算法将加权的空手道俱乐部也划分成了两个社区,仍用圆和正方形标记以示区分,节点之间边的粗细代表权重大小,边越粗代表这条边的权重越大。其中9号节点表示重叠节点。相比较无权数据集,加权后的俱乐部中的3号和20号成员不再是“中立成员”,都向正方形社区倒戈。对于3号节点而言,尽管与两个社团交流都十分密切,但是从图中可以直观地看出,在节点影响力差不多的情况下,1号和2号节点与3号节点之间边的权重明显高于其他节点,因此正方形社区的边影响力更大,导致3号节点被划分进了正方形社区。对于9号节点所有的连边中,与3号节点的连边的权重是最大的,直观并无法分辨9号节点应该属于哪个社区,COPRA-PI算法将其归为重叠节点也是合理的。

4 结 语

本文提出了一种基于传播影响力的加权重叠社区发现算法。该算法将边的权值与节点的度结合,采用节点强度表示加权网络中节点的度,将加权网络转化为无权网络进行处理。算法通过定义节点标签概率矩阵,表示节点拥有每个标签(属于某个社区)的概率大小来实现社区重叠,即一个节点可以同时属于不同社区,并且记录属于每个社区的概率。标签概率矩阵由传播影响力决定,即节点影响力、边影响力和历史标签影响力。在迭代传播的同时进行标签过滤,直至完成社区发现。实验结果表明所提出的算法充分考虑了可能影响节点所属社区的因素,相比较其他两种经典的重叠社区发现算法表现出了更高的社区划分质量。

[1] FORTUNATO S.Community detection in graphs[J].Physics Reports,2010,486:75-174.

[2] ME N.Fast algorithm for detecting community structure in networks[J].Physical review.E,Statistical,nonlinear,and soft matter physics,2004,69:066133.

[3] GIRVAN M,NEWMAN M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences of the United States of America,2002,99(12):7821-7826.

[4] RAGHAVAN U N,ALBERT R,KUMARA S.Near linear time algorithm to detect community structures in largescale networks[J].Physical Review.E,Statistical,nonlinear,and soft matter physics,2007,76(3):036106.

[5] JIN D,LIU J,JIA Z X,et al.K-nearest-neighbor network based data clustering algorithm[J].Pattern Recognition&Artif i cial Intelligence,2010,23(4):546-551.

[6] ZHANG X K,FEI S,SONG C,et al.Label propagation algorithm based on local cycles for community detection[J].International Journal of Modern Physics B,2015,29(5):1550029.

[7] PENG H,ZHAO D,LI L,et al.An improved label propagation algorithm using average node energy in complex networks[J].Physica A Statistical Mechanics&Its Applications,2016,460:98-104.

[8] PALLA G,DERE NYI I,FARKAS I S,et al.Uncovering the overlapping community structure of complex networks in nature and society[J],Nature,2005,435(7043):814-818.

[9] GREGORY S.Finding overlapping communities in networks by label propagation[J].New Journal of Physics,2010,12(10):2011-2024.

[10]LANCICHINETTI A,FORTUNATO S,KERTESZ J.Detecting the overlapping and hierarchical community structure of complex networks[J].New Journal of Physics,2008,11(3):19-44.

[11]SHEN H W,CHENG X,CAI K,et al.Detect overlapping and hierarchical community structure in networks[J].Physica A Statistical Mechanics&Its Applications,2008,388(8):1706-1712.

[12]MEGHANATHAN N.A greedy algorithm for neighborhood overlap-based community detection[J].Algorithms,2016,9(1):8.

[13]BLONDEL V D,GUILLAUME J,LAMBIOTTE R,et al.Fast unfolding of communities in large networks[J].Journal of Statistical Mechanics-Theory and Experiment,2008,2008(10):155-168.

[14]BAI X,YANG P,SHI X.An overlapping community detection algorithm based on density peaks[J].Neurocomputing,2016,226:7-15.

[15]杨贵,郑文萍,王文剑,等.一种加权稠密子图社区发现算法[J].软件学报,2017,28(11):3103-3114.

[16]刘世超,朱福喜,甘琳.基于标签传播概率的重叠社区发现算法[J].计算机学报,2016,39(4):717-729.

[17]NEWMAN M E J,GIRVAN M.Finding and evaluating community structure in networks[J].Physical Review.E,Statistical,Nonlinear,and Soft Matter Physics,2004,69(2):026113.

[18]乔少杰,韩楠,张凯峰,等.复杂网络大数据中重叠社区检测算法[J].软件学报,2017,28(3):631-647.