多场耦合下微波碳热氯化回收铟的动态仿真

关 杰,刘美玲,苏瑞景

(上海第二工业大学 环境与材料工程学院,上海201209)

0 引 言

稀有金属铟及其化合物具有优良的物化性质,被广泛应用于通信、工业、军事等重要领域。但全球预估铟储量仅5万t,铟的天然存在形式主要以极低含量伴生于闪锌矿等矿石中,约1～100 mg/kg。目前原生铟主要利用化学法从伴生矿物的冶炼烟尘、熔渣等副产品中提取[1-2]。但随着使用铟锡氧化物ITO[m(SnO2):m(In2O3)=1:9]靶材的平面液晶显示器(liquid crystal display,LCD)等产品数量激增,全球每年70%以上的铟被用于生产LCD,但该类产品寿命不长且更新较快,且LCD中铟的含量为250 mg/kg以上,因此具有很高的回收价值。同时,大量废弃LCD也成为再生铟的重要途径[3]。

从LCD中回收铟的传统方法主要为火法和湿法。随着科技发展,微波冶金作为新型技术快速进入人们的视线。微波在冶金工程中主要用途为辅助萃取、浸出、消解、合成、碳热等[4-7]。由于InCl3是生产ITO的重要原料,以微波辅助碳热氯化反应回收金属铟存在可行性,关杰等[8-10]利用碱溶LCD玻璃基板粉末脱除硅、铝,提高了氯化法回收铟化物的效率。虽然有相关的实验结论支撑,但在多相反应场中,如何有效的传热、传质是提高回收率的重要条件,不过相关研究较少,因此对于进一步研究铟化物回收过程中的射频-温升-流体-化学反应等物理场耦合对产物回收的影响有其必要性。

本文的研究目的是在前期实验研究基础上,基于COMSOL Multiphysics软件有限元求解方式,对微波碳热氯化提铟过程进行多场耦合数值分析,探究微波输入功率、气体流量、样品位置对反应过程的影响,为优化腔体结构和反应体系设计提供参考。

1 射频-温升-流体-化学反应耦合物理模型

对于本次射频-温升-流体-化学反应耦合物理模型计算,需要结合微波传输控制方程、热量交换过程控制方程、流体动力学控制方程与物质传输过程的控制方程[11-14]。

(1)对于常规的微波传输问题,其控制方程为：

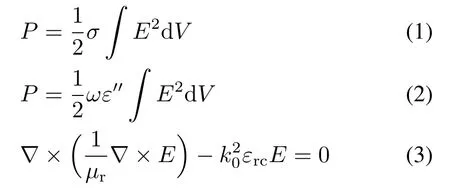
对于时谐和特征值问题,自由空间的波数k0可以表达为：

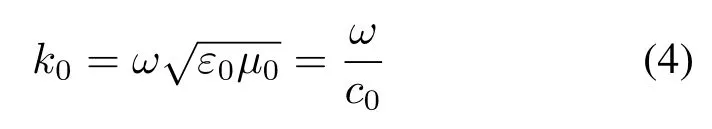
式中,P为微波功率,W;σ为物料的电导率,S/m;ε′′为物料复介电常数的虚部;▽为旋度计算;µr为材料的相对介电常数;εrc为材料的相对磁导率;E为电场强度,V/m;ω为电磁波的角频率,Hz;µ0为真空介电常数,F/m;c0为真空中的光速,m/s。

(2)热量交换过程的控制方程为：

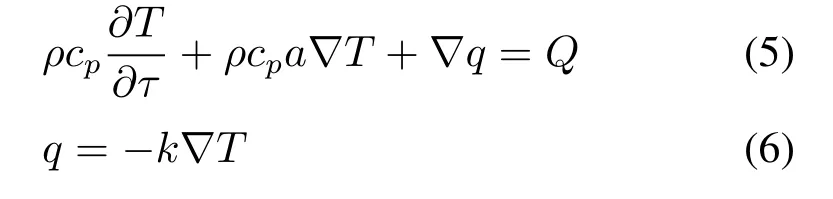
式中,ρ为固体或者流体密度,kg/m3;cp为质量定压热容,J/(kg·K);k是热导率,W/(m·K);a为对流换热速度,m/s;▽T为温度梯度,K/m;Q为热源项,W/m3。Q由微波加热和热解反应焓变组成,其表达式为：

式中,Qe是由微波热源,由阻抗热Qrh和磁损失Qml组成,其表达式分别为：

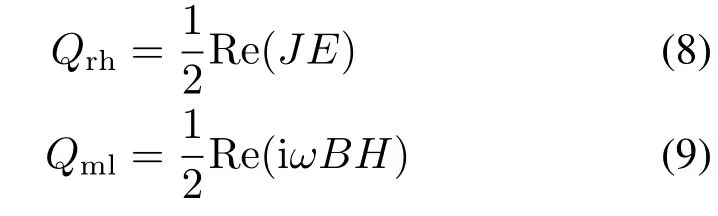
式中:Re为求实部的内置函数;J为电流密度,A/m2;i为单位虚数;B为磁通量,T;H为磁场强度,A/m。

(3)对于HCl气体的流体动力学控制方程可以包含质量连续方程和动量连续方程两部分。

质量连续方程为:

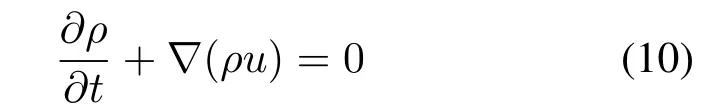
式中,ρ为流体密度,kg/m3;t为时间,s;u为流体速度,m/s。

动量连续方程为：

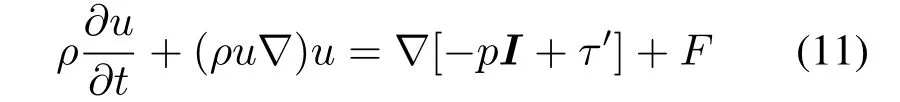
式中,p为压强,Pa;I为单位矩阵;τ′黏性剪切力,Pa;F为体积力,一般为重力或电磁场力,N。(4)HCl与In2O3的主反应方程式如下[8]:

主反应的物质传输过程的控制方程为：

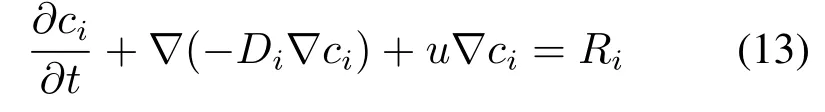
式中,i为 HCl或 InCl3;ci为 i物质的量浓度,mol/m3;Di为i物质的扩散系数;Ri为反应速率,其阿雷尼乌斯公式:

R为气体常数,J/(mol·K);Ai为物质的反应指前因子;Ea为i物质的反应活化能,J/mol;T为温度,K。

联立上述方程即为全耦合法射频-温升-流体-化学反应分析的数学物理模型,在给定边界条件和初值时,可进行数值求解。其耦合逻辑关系如图1所示。

图1 多物理场耦合关系图Fig.1 Multi-physical f i eld coupling diagram

由于相关控制方程均带有偏微分算子,在方程组求解时对边界条件及初始条件的限制通常过于复杂且要求函数有较高的正则性,在这样的限制下有时并不能直接进行求解。然而通过引入广义解,即通过弱化对方程解的要求[14],使其更加离散且同时满足弱形式方程和强形式方程,从而得出正确且收敛的结果,以降低对初始条件、边界条件、积分变量连续性等的要求。弱解形式非常适合求解非线性多物理场耦合问题,所以在COMSOL中物理场的偏微分方程组首先通过积分将方程转化为弱解形式,然后再进行求解。

本研究的物理模型综合考虑物理的合理性、模型的收敛性、求解时间及关注变量等因素的情况,做出如下假设。

(1)所有物质均为各向同性的均值材料,即其密度、黏度、传热系数、相对介电常数等在各个方向所测得的性能数值完全一致,均为常数。

(2)由于气体流速较低且密度对反应影响较小,认为其流动过程密度变化可以忽略,将其简化为不可压缩流体,并且流场率先达到稳态分布,并认为在本次仿真中流场已达到稳态。

(3)由于副反应情况复杂,根据已有的实际反应研究结果可知[8],通过对氧化铟回收体系实施温度控制可以降低副反应的发生、促进目标产物的生成。因此,在本次仿真中忽略氧化铟回收过程中的副反应,只考虑主反应方程式(12)的进行,反应物定为碳与氧化铟的混合粉末。

(4)尽管InCl3在回收过程中由于温度变化会产生相变,但只对最终实际回收产生影响,并不参与碳热氯化提铟反应过程,因此为提高模型收敛性并缩短求解时间,忽略InCl3在不同温度下的相变问题。

(5)实际过程中换热方式分为：热传导、对流换热、热辐射,但由于样品制备为碳和氧化铟的粉末混合物,其表面发射率较难测定,且样品对外界的热辐射在本次实验中的影响远小于热传导与对流换热,因此本文中暂时只考虑热传导和对流换热2种换热方式,不考虑辐射换热的方式。

(6)反应速率方程如阿雷尼乌斯式(14)描述,限于实验条件暂时忽略反应物浓度的影响。

在物理场求解的过程中,本文选用稳态-瞬态-频域3种方法求解4个物理场。其中,流场求解采用MUMPS求解器,射频、温度和反应采用几何多重网格求解器,循环方式为V循环,多重网格层数为1,粗化因子为2,预平滑器和后平滑器采用SOR矢量求解器,粗化求解器采用MUMPS求解器。设置可以有效保证求解效率和收敛性。

2 计算模型

2.1 研究对象

本研究样品选用InCl3与碳的均匀混合粉末。微波由腔体左侧端口输入,腔体内放置石英管,管中放置金属支架,将样品平铺于支架上,HCl气体由石英管下方端口处向上通入[8],并与样品发生化学反应,生成的InCl3随HCl从石英管上端口流出,模型参数见表1,腔体三维图如图2所示。

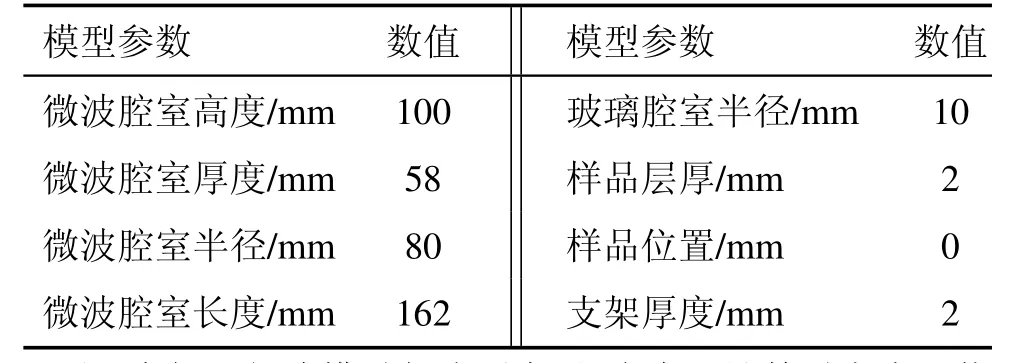
表1 几何模型参数表Tab.1 The parameters of geometric model

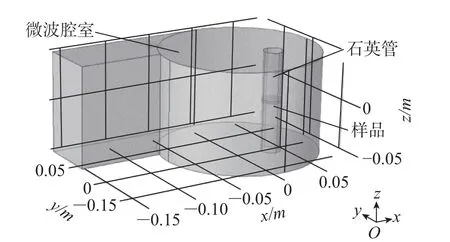
图2 腔体三维图Fig.2 3D f i gure of the cavity

采用COMSOL软件自带的几何建模工具完成三维实体建模,采用四面体网格剖分,选择二阶常规尺寸单元对几何模型进行网格剖分,并对流体域进行边界层网格剖分,得到离散化网格,总计17 992个四面体单元,如图3所示。

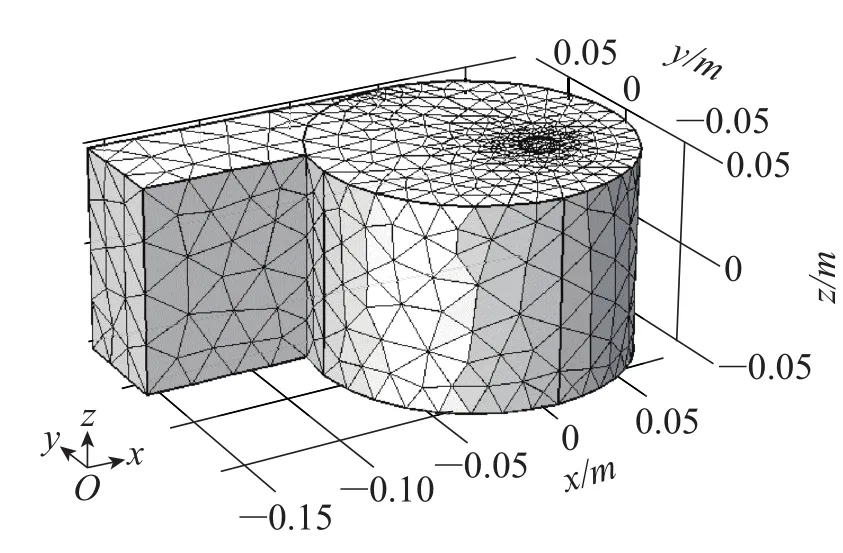
图3 四面体网格剖分图Fig.3 The tetrahedron mesh sketch

2.2 物性参数设置及定解条件

偏微分方程要得到定解必须在求解前给出合适的边界条件和初始值。本实验在射频-温升-流场-化学反应耦合模型中,分别给出以下边界条件。

(1)射频-频域物理场的边界条件。端口设置为矩形端口,加载微波TE 10模式,模式相位为0 rad,余下所有边界设置为阻抗边界,阻抗大小为微波腔体壳体实际测量值。

(2)在固体-流体传热物理场的边界条件。流场设定已达到稳态,HCl流出端边界上仅存在对流换热;其余外部边界为自然对流换热边界条件,其换热系数h=5 W/(m2·K),环境温度为室温。

由于石英管存在金属支架,故需要采用内部边界条件来描述该支架对系统传热性能的影响,在该边界处需要描述的条件包括耦合流场、支架的几何尺寸和密度、热容及导热系数。

(3)在流体动力学物理场的边界条件。HCl气体通入端设为变量,流出端为常压边界。由于管内存在金属支架,故在流场中仍需要采用内部边界对其进行描述,在此将金属直接简化为多孔格栅,设置其几何形状参数。

(4)在热解反应物质传输物理场的边界条件。HCl气体通入端浓度设为变量,所有物理场的初始值均可以采用默认的0设置,COMSOL可以自动根据边界条件进行初值判断,得到自洽的实际计算初始值。

本文多物理场模型的部分物性参数如表2所示[15]。

表2 物性参数表Tab.2 Physical parameters list

3 仿真结果分析

3.1 微波功率对温升的影响

运用COMSOL Multiphysics的参数化扫描求解功能依次求解了微波输入功率分别为300、500、700 W时的回收过程。

图4所示为样品的温度分布图。从整体上看,样品放置在圆形谐振腔中心位置,在不同输入功率下,样品内部各点处的温度分布趋势相似,但样品体温度分布不均匀,左侧温度较高,右侧较低,该现象与样品放置位置和腔体与馈口位置相关。随着微波功率增大,相对的高温区面积减小,温度不均匀程度加剧。加热10 min后,微波输入功率P=300 W的样品的最高温度为175°C,最低温度为152°C,温差为23°C;P=500 W时,样品最高温度为519°C,最低温度为397°C,温差122°C;P=700 W时,样品最高温度为724°C,最低温度为548°C,温差176°C,温差不断增大。微波功率增大,样品整体温度升高,有利于主反应进行,但样品温差增大不利于实际条件下控制副反应,在实际操作中可以通过改变混合方式、加入其他导热剂、优化腔体设计提高温度分布的均匀性,从而进一步提升在相同时间内样品InCl3的回收率,同时提升HCl的利用率。

以样品的中心点(0,0,0.001)处温度代表样品平均温度,调整微波功率300、400、500、600、700 W,得到中心点处在不同微波输入功率下温度随时间的变化,如图5所示。观察图5(b)可知,温度增长分为两部分,在温度相对低的时候基本呈线性增长,但当样品温度达到350°C附近时,随着样品加热时间继续增加,样品温度呈对数形式增长,相关的线性方程与对数方程见表3。将温度变化分为2段后,所得的拟合方程相关系数R2均大于0.99,说明拟合效果较好,可以用于结论的分析。由于样品的相对介电常数随温度变化,在温度达350°C左右时可能出现了临界点,突破临界点后升温速率大幅提升。该现象也反映出当样品整体平均温度被提升至350°C以上时,可以获取较快的反应速率。

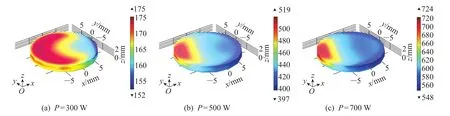
图4 加热10 min后样品的温度分布图Fig.4 The sample temperature distribution diagram after 10 min heating

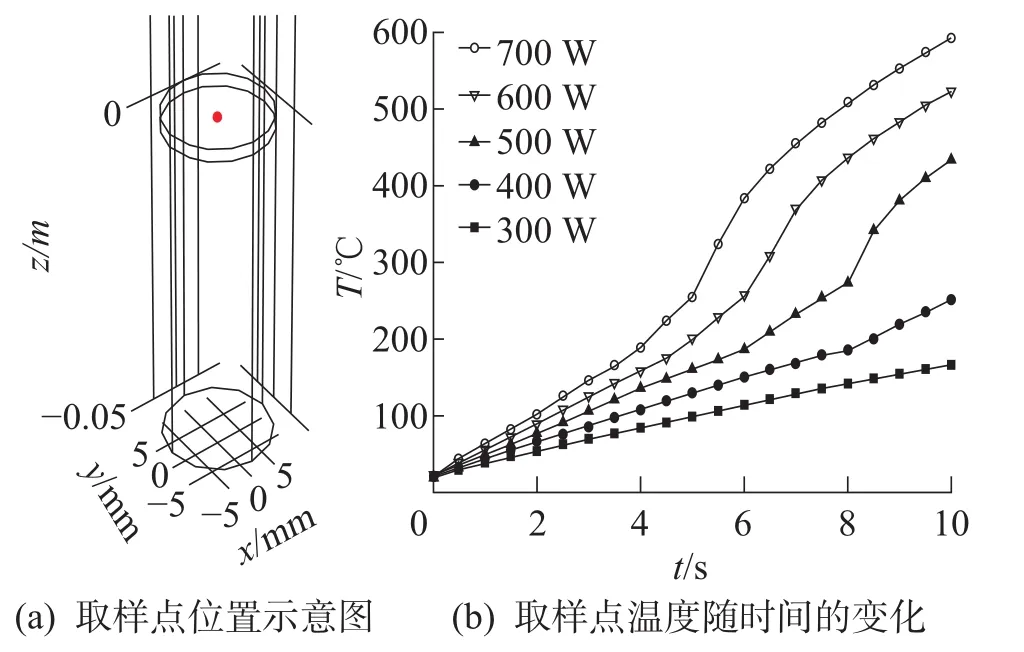
图5 样品中心点温度随时间的变化Fig.5 The temperature of sample center varies with time

表3 温度随时间的变化拟合方程Tab.3 The f i tting equation of temperature varies with time

3.2 HCl浓度对反应的影响

根据主反应的需求,选定微波输入功率P=500 W,并设定HCl气体通入浓度分别为0.1、0.3、0.5 mol/L,得到管内的HCl浓度分布纵切面图(见图6)及相应的InCl3的浓度分布切面图与五横截面图(见图7)。

从图6(a)、(b)、(c)的总体趋势可以看出,在下方未反应区,由于存在边界层,靠近管壁位置流速变低,浓度升高。进入反应区,靠近管壁的位置浓度较管中心处更低,表明通入高浓度的HCl有利于反应进行。根据图7的InCl3的结果可知,在一定范围内,通入不同浓度的HCl气体对InCl3的生成几乎没有影响。结合样品温度分布情况可以得出,在总趋势上,反应区内样品温度较高的一侧InCl3的浓度较高,右侧温度较低的部分InCl3生成的浓度较低。在温差和浓度差作用下向右上方扩散。3种HCl通入浓度下,InCl3的浓度最大值分别为9.29、9.31、9.31 mol/m3,变化量为0.2%,表明在一定范围内,HCl气体的通入浓度对InCl3的生成及浓度分布影响不大。

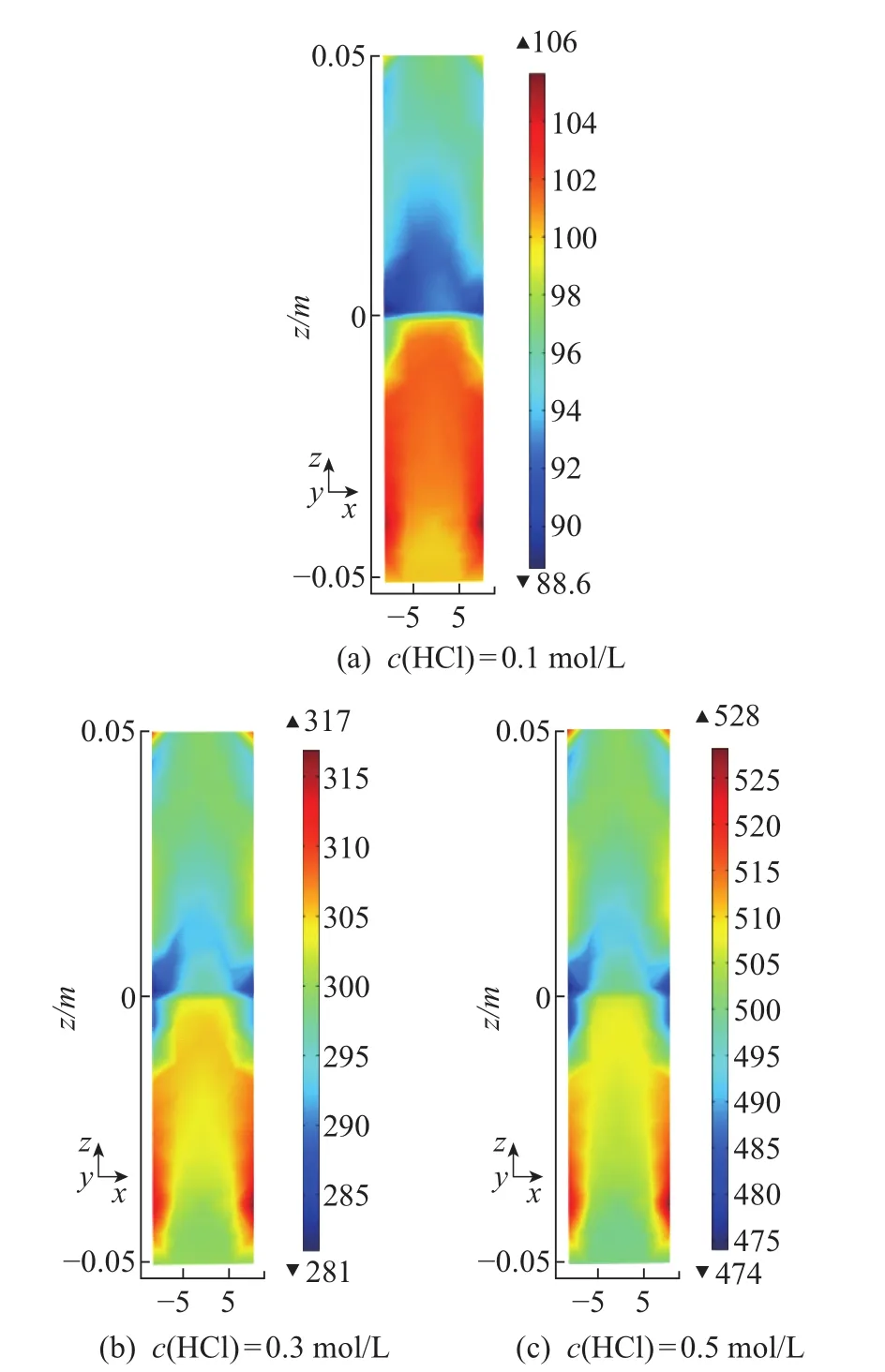
图6 管内HCl的浓度分布切面图(t=5 min)Fig.6 The concentration distribution diagram of HCl in the tube(t=5 min)

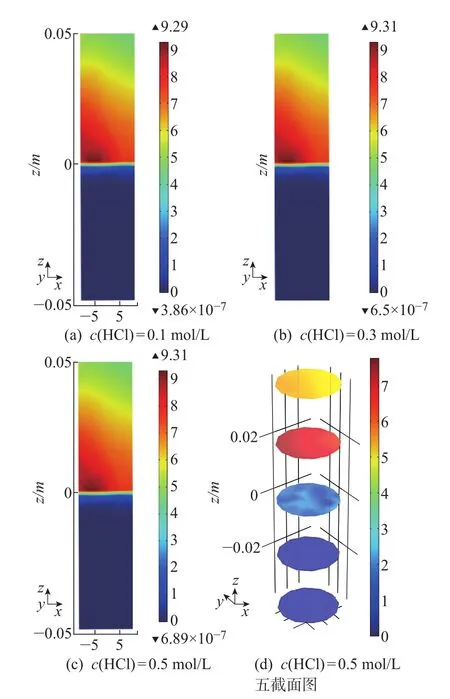
图7 管内HCl的浓度分布切面图(t=5 min)Fig.7 The concentration distribution diagram of InCl3in the tube(t=5 min)

图8 管内InCl3的浓度分布图(t=10 min)Fig.8 The concentration distribution diagram of InCl3in the tube(t=10 min)

3.3 微波功率对反应的影响

根据以上结果及实际需求,选定HCl通入浓度为0.5 mol/L,排除了HCl通入浓度对反应产物的影响,改变微波输入功率,可以得到管内InCl3浓度分布多切面图与五截面图,如图8所示。结果表明,随着输入功率增大,管内InCl3的浓度升高,且产物浓度与样品体、管内气体温度正相关,其浓度的最大值分别为9.471、89.2、152.9 mol/m3。由于功率与温升的关系并非完全线性,因此浓度值的变化呈非线性增长。

微波输入功率是氯化提铟过程中最主要的热源项,对多场耦合下样品体温度、流体温度、化学反应、反应物与产物浓度变化均有明显影响。

4 结论与展望

本文基于COMSOL Multiphysics建立了射频-温升-流体-化学反应多物理场全耦合分析模型,研究了电磁热流反应耦合作用对微波碳热氯化提铟回收工艺的影响,主要得到以下结论:

(1)采用COMSOL Multiphysics建立的多物理场耦合模型可以实现电磁场-温度场-流场和化学反应的全耦合分析,并用于研究各变量耦合作用的影响;

(2)在样品的升温过程中,微波辐射热源是样品温度变化的主要原因,样品温度与InCl3的浓度和反应速度正相关,但是在一定范围内,HCl气体的通入浓度对InCl3的生成几乎无影响。因此研究微波加热过程对氯化提铟的反应有着重要意义;

(3)研究微波加热过程对微波腔体的设计也需要理论支撑,在未来的实验研究中,优化微波腔体十分必要。

[1] 侬健桃.我国铟产业现状及发展[J].中国有色冶金,2002,31(4):12-14.

[2] 黎铉海,马宸,俸余,等.硫化铟常压硫酸浸出动力学研究[J].金属矿山,2011(6):89-92.

[3] YANG J,RETEGAN T,EKBERG C.Indium recovery from discarded LCD panel glass by solvent extraction[J].Hydrometallurgy,2013,137:68-77.

[4] 崔维,王仕兴,彭金辉,等.微波能技术在贵金属领域的应用与发展[J].稀有金属,2015,39(7):652-659.

[5] 王欣.微波碳热还原-超声波强化浸出富铟锌渣的研究[D].昆明：昆明理工大学,2013.

[6] HIGASHIA,SAITOHN,OGIT,etal.Recoveryoflndium by biosorption and its application to recycling of waste liquid crystal display panel[J].Journal of the Japan Institute of Metals,2011,75(11):620-625.

[7] VIROLAINEN S,IBANA D,PAATERO E.Recovery of indium from indium tin oxide by solventextraction[J].Hydrometallurgy,2011,107(1):56-61.

[8] 任浩华.基于PVC热解生成HCl氯化回收LCD中的铟[D].北京：中国矿业大学,2015.

[9] 王帅,关杰,任浩华,等.低温碱溶脱除液晶显示器(LCD)玻璃基板粉末中的硅和铝[J].环境工程学报,2015,9(12):6078-6082.

[10]GUAN J,WANG S,REN H H,et al.Indium recovery from wasted liquid crystal display by polyvinyl chloride wastes[J].RSC Advances,2015,5(124):102836-102843.

[11]孔珑.工程流体力学[M].北京：中国电力出版社,2014.

[12]苏石川.热能工程与先进能源技术仿真与设计[M].北京：化学工业出版社,2015.

[13]彭沛夫,张桂芳.微波与射频技术[M].北京：清华大学出版社,2013.

[14]谷超豪.数学物理方程.3版[M].北京：高等教育出版社,2012.

[15]LIDE D R.CRC handbook of chemistry and physics[M].Boca Raton,FL,USA:CRC Press,2007.