基于轴心轨迹自动辨识的高速主轴系统故障诊断研究
2018-07-04张洪生
崔 立,张洪生
(上海第二工业大学工学部,上海201209)
0 引 言
高速主轴系统作为数控机床的关键部件,它的性能直接决定了数控机床的加工性能,一旦主轴系统精度丧失或出现故障,必然导致机床整体运行不正常,甚至引发灾难性的后果,因此对运行中的机床主轴系统进行故障诊断,近年来引起了广泛关注。轴心轨迹因可反映主轴系统不同的运动状态或故障信息,是机床主轴系统振动信号分析的重要内容。轴心轨迹图是从主轴某一截面测得的相互垂直方向上的振动信号,由轴心轨迹图形状对主轴系统故障进行诊断,对于机床运行状态监测具有较重要的意义。
目前,对轴心轨迹的理论计算研究已经较为成熟[1]。实际测试得到的轴心轨迹由于噪声干扰提取问题近年来受到广泛关注,小波降噪是目前较常用的研究方法,但小波或小波包分解方法可能会造成细节信号丢失且各频带间能量具有相互交叠问题[2],而谐波小波方法由于可实现在同一层信号局部频谱的细化分析,可用于轴心轨迹分析得到提纯后的轴心轨迹[3]。中值滤波是常用的一种非线性平滑滤波,它既可以保护图像边缘信息又可以对图像中无用的脉冲噪声进行消噪,可以使图像平滑。本文结合中值滤波和小波滤波各自的优点,基于中值滤波方法对脉冲噪声滤波、使用谐波小波对受高斯噪声干扰的像素滤波,给出了一种轴心轨迹图像混合消噪方法。轴心轨迹特征提取目前常用方法有:矩方法、几何特征法、编码方法等,关于轴心轨迹特征提取以HU氏7个不变矩最为常用[4],但理论及实验分析表明,HU氏不变矩有一定的局限性[5]。袁倩等[6]采用DS证据理论对轴心轨迹特征参数进行融合识别诊断,能有效地对轴心轨迹进行识别。本文采用线矩计算不变矩用于轴心轨迹的识别。对于高速机床主轴的故障诊断,神经网络、灰关联分析方法、支持向量机等方法应用较为广泛[6-7],其中BP神经网络具有收敛速度快、识别准确等特点[8-11],本文选用BP神经网络进行高速主轴故障诊断的研究。
本文结合中值滤波和小波滤波去除轴心轨迹中的脉冲噪声和高斯噪声,将轴心轨迹转换成轴心轨迹图像然后计算采用线矩计算不变矩,基于BP神经网络实现高速主轴系统的故障诊断。
1 轴心轨迹图像处理与特征识别模型
轴心轨迹图像监测高速主轴系统运行过程中的振动情况,是高速旋转机械故障诊断中的常用的诊断方法。采用两个电涡流位移传感器监测主轴的互为90°夹角的两个方向的径向位移,将所测位移数据在坐标系中合成得到轴心轨迹图像。在高速主轴系统中,为使电涡流传感器能准确测量主轴振动情况,将传感器安装在紧靠支撑轴承处。由于在该点,轴的刚度较高,因此轴心轨迹的变化可以较准确地反映主轴系统的运行特征,电涡流位移传感器在主轴系统实验台的安装如图1所示。
为提高轴心轨迹辨识的准确性,首先需要对图像进行边缘检测和消噪处理,对轴心轨迹图像进行归一化处理并经过灰度调节后进行边缘检测。然后,基于中值滤波方法将脉冲噪声检测出来并进行滤波,并对受高斯噪声污染的像素采用谐波小波滤波。接着,是图像的特征识别,由于轴心轨迹图形经消噪处理后得到的是轮廓线图,因此采用线积分取代面积分,用线矩来计算不变矩。
本文先对测得的轴心轨迹位移数据作图得到轴心轨迹图形,再对其填充得到轴心轨迹图像,接着进行边缘检测和消噪处理并计算不变矩。

图1 位移传感器在实验台上的安装Fig.1 Sketch map of the installation of distance sensor
1.1 基于中值滤波和谐波小波法的轴心轨迹处理
中值滤波可以消除孤立的噪声点,对图像中无用的脉冲噪声进行消噪,表达式如下:

式中:W 是平面窗口尺寸;m是窗口水平尺寸;n是窗口垂直尺寸;Xij是被处理的图像平面上的一个像素点,坐标为(i,j);Yij是窗口范围内像素点灰度的中值;Z2是二维数据串的序号。
1993年,Newland构造出了具有紧支特性和极好的“盒形”谱特性的谐波小波,其频域的广义表达式为[3]

式中:m、n为小波变换的层次参数,其中m=2j,n=j+1。此时相应的小波变换为

给定谐波小波位移步长k/(m−n),则式(3)变为


式中:2π(m−n)为带宽,分析中心在x=k/(m−n)的谐波小波表达式。
1.2 改进的不变矩计算模型
对于轴心轨迹图形,定义轴心轨迹的p+q阶矩为[4]:

式中:f(x,y)表示图像在(x,y)的灰度值;mpq可以唯一确定f(x,y)。
质心坐标表达式为:

定义满足平移不变性的中心矩为:

对上式表述的中心矩进行归一化处理,得
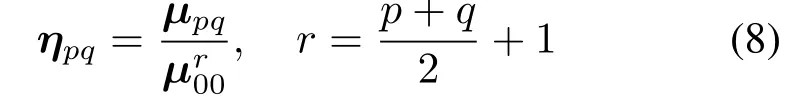
由式(8)归一化的中心矩,可定义7个不变矩函数:

2 基于神经网络的轴心轨迹故障诊断
高速主轴系统的轴心轨迹图像包括着各种故障信息,本文选取两种最常见的主轴故障进行研究:主轴不对中和不平衡。如果主轴系统出现轻微不对中故障,则轴心轨迹大致呈椭圆形;如出现中等不对中故障,轴心轨迹则大致呈香蕉形;如出现严重不对中故障,会使轴心轨迹图呈现外“8”字形。主轴不平衡故障的识别特征是轴心轨迹为大圆形,且故障越严重圆形越大。
在实验室使用高速主轴轴承系统试验器进行主轴正常、不对中和不平衡故障实验,如图2所示。采用GMN转速达42000 r/min的电主轴驱动试验器,采用型号为ZA21电涡流位移传感器和BZ2109型电荷滤波积分放大器进行振动位移监测。测试系统采用PC总线兼容的数据采集卡BH5115,最大采样频率为100 kHz,数据采集模块通过软件触发模式启动A/D转换,使用上位机实现数据采集。
针对不对中和不平衡故障,分别通过调整联轴器位置、以及试验器主轴上不平衡质量块,来设定轻度、中度、重度3种故障程度进行实验,根据故障严重程度将故障从0到1定义。设置采样频率为2kHz,主轴转速为8000 r/min,分别记录两个位移传感器在主轴正常、主轴存在轻度、中度、重度不对中故障和不平衡故障的振动位移信号,水平、垂直方向测得的位移信号分别定义为x和y方向信号。

图2 高速主轴轴承系统实验器Fig.2 Test rig for high-speed rotor bearing system
本文编制了主轴系统故障诊断软件,软件使用MATLAB、VB语言编写,其中VB用来进行数据采集、编辑界面,MATLAB用来计算和获得图形,使用ActiveX技术调用MATLAB程序。首先对主轴系统的高频振动信号数据采集,采集界面如图3所示。然后使用MATLAB信号处理工具箱函数实现中值滤波和谐波小波消噪。
接着,使用MATLAB建立的BP神经网络对主轴系统进行故障诊断[12],神经网络的训练规则采用误差反向传播规则,即BP算法。建立3层神经网络模型:输入层I、隐含层II、输出层III,如图4所示。输入层为提取的不变矩特征,设置隐含层节点数为12,主轴状态的故障编码即BP神经网络的输出。根据主轴发生的故障类型,确定了3种工作状况,分别为正常状态(0,0,0);不对中(0,F,0);不平衡(0,0,F),其中F为0到1的数值,代表故障程度大小,输出层节点数设置为3,设定收敛精度为0.001。

图3 高速主轴系统监测界面Fig.3 Monitoring interface

图4 神经网络模型图Fig.4 Model of the neural network
高速主轴系统轴心轨迹故障诊断流程如图5所示。对采集到的信号进行降噪处理得到轴心轨迹图像,图6所示给出了其中一组数据,分别为主轴正常、存在不平衡故障和不对中故障试验降噪前后的信号,可见消噪后轴心轨迹特征更加明显。接着进行不变矩特征提取,部分数据如表1所示。

图5 高速主轴系统故障诊断流程图Fig.5 Flow chart for fault diagnosis of high-speed spindle system

图6 降噪前后的轴心轨迹Fig.6 Axis orbit before and after de-noising

表1 实验测得的不变矩Tab.1 The invariant moments measured by experiment
选取90组样本数据计算其轴心轨迹不变矩,对建立的BP神经网络进行训练,训练132步后达到目标值,训练过程如图7所示,此时软件可用于主轴系统的故障诊断。

图7 神经网络训练过程图Fig.7 Neural network training process
3 轴心轨迹故障诊断实验
利用图2所示的高速主轴轴承系统试验器进行试验验证,针对该主轴正常、不对中状态、不平衡状态,采集主轴两个方向振动信号。使用图7训练好的BP神经网络进行主轴系统故障诊断实验。表2给出了BP神经网络对测试样本的诊断率,测试平均准确率达到 96%,表明本文提出的方法可以快速准确地对主轴正常、不对中、不平衡故障进行诊断和评估。

表2 神经网络对测试样本的诊断率Tab.2 Diagnosis rate of test samples by neural network
4 结 论
(1)提出了一种基于轴心轨迹图像进行主轴转子系统故障诊断新方法,结合中值滤波和小波滤波去除轴心轨迹中的脉冲噪声和高斯噪声,将轴心轨迹转换成轴心轨迹图像然后计算采用线矩计算不变矩,基于BP神经网络实现高速主轴系统的故障诊断。将该方法应用于高速主轴系统的不对中、不平衡故障诊断,验证了本文方法的有效性,为高速主轴系统故障诊断提供了一种新方法。
(2)该方法用于高速主轴系统正常、不对中故障、不平衡故障的诊断,实验表明诊断准确率为96%。为提高数控机床主轴系统的可靠性提供了保障。
[1] 徐小力,王红军.大型旋转机械运行状态趋势预测[M].北京:科学出版社,2011.
[2] 李方.谐波小波在设备故障诊断中的应用[D].武汉:武汉科技大学,2005.
[3] 陈果.一种改进的谐波小波及其在转子故障诊断中的应用[J].机械工程学报,2011,47(1):8-16.
[4] 王广庆,万书亭.基于改进的图形不变线矩的转子轴心轨迹形状的自动识别[J].振动与冲击,2006,34(11):342-344.
[5] 袁倩,孙冬梅,范文.基于D-S证据理论的轴心轨迹自动识别方法[J].机床与液压,2017,45(6):167-171.
[6] GAGNOL V,BOUZGARROU B C,RAY P,et al.Modelbased chatter stability prediction for high-speed spindles[J].International Journal of Machine Tools&Manufacture,2007,47(7):1176-1186.
[7] 孙斌,薛广鑫.基于等距特征映射和支持矢量机的转子故障诊断方法[J].机械工程学报,2012,48(8):128-135.[8] 张冉,赵成龙.改进BP网络在汽轮发电机组故障诊断中的应用[J].计算机仿真,2011,28(6):325-328.
[9] 甄敬然,雷钢.数控机床主轴故障诊断方法研究[J].制造业自动化,2014(10):72-75.
[10]刘金辉,任小洪.LM算法BP神经网络的数控机床主轴系统故障诊断[J].机床与液压,2015,43(21):193-196.
[11]李善,谭继文,俞昆.神经网络和改进D-S证据理论相结合的滚动轴承复合故障诊断研究[J].机床与液压,2018(1):153-157.
[12]丁平,徐桂云,石晓妹,等.基于Matlab的转子典型故障诊断与分析[J].轴承,2010(7):36-38.
