基于Kriging代理模型的城轨车轮踏面外形优化
2018-07-04施振宇邢宗义
施振宇,戴 硕,邢宗义
(南京理工大学自动化学院,南京 210094)
为了减轻交通压力以及降低环境污染,城市轨道交通的发展开始加速。城市轨道交通载客量大、安全准点,能够满足人民群众的日常出行,而且具备节约土地资源以及环保的优势,与人民群众生产生活密切相关[1]。地铁的运行线路与普通铁路不同,弯道较多且曲线轨道半径小,需要经常性的启动和制动,造成轮轨接触关系分析变得困难起来。随着累计行程的逐渐增加,轮轨之间的损耗加大,造成轮轨系统性能变差,从而危害车辆运行的安全行驶,极大阻碍了城市轨道交通的发展[2]。城轨车轮磨耗除了使得轮缘轮径的尺寸减小之外,同时踏面外形轮廓也会因此发生较大变化。部分地铁线路运行一段距离之后轮缘发生磨损,出现踏面剥离、擦伤和平轮等形式的损伤[3]。而车轮踏面磨耗严重也会导致轮对寿命远低于正常的使用周期[4]。踏面剥离是指由于持续的运营导致轮轨接触疲劳,致使踏面表面出现剥落,产生裂纹,此时须进行镟修,若出现磨耗超限则要及时更换,这将会产生一定的费用并大大减少轮对使用寿命[5]。轮轨外型不匹配将导致列车平稳性与曲线通过性能差、较大的轮轨接触应力、踏面严重磨损和出现裂纹、运行中噪声等一系列的问题,严重时甚至会引起列车脱轨等重大交通事故[6]。因此采用恰当的车轮踏面外形,可以减少轮轨之间的磨损,节约成本和减少维修次数,提高车轮的稳定性,增加使用寿命,改善车辆的动力学性能。
常崇义等[7]采用ABAQUS建立了三维动态轮轨接触有限元模型,以现场试验得到的实测数据对数值分析模型和方法进行了验证。BRAGHIN等[8]应用基于简化FASTSIM算法对轮轨关系进行了计算分析,研究出当车辆行驶超过20万km再进行镟轮作业,能够将轮对的使用寿命延长一倍以上。员华等[9]对轮对镟修工作现行采用的等级镟修制度进行了分析,选择不同的轮缘厚恢复等级进行镟修,尽可能减少轮径的镟削量。PASCUAL等[10]分析研究城轨车轮轮对磨耗实测历史数据,认为当轮缘厚度下限为27.5 mm,镟修后的轮缘厚度值为30.5 mm时产生的轮对镟修总费用是最小的。许宏等[11]基于高斯过程建立了轮对磨耗模型,采用蒙特卡罗仿真进行求解,实现镟修参数的优化。王珍[12]通过对动车组历史数据的分析,确定了单个车轮的最优镟修参数选择。Jendel[13]将车辆轨道动力学仿真计算放在时域进行,并在Gensys软件中进行模拟。
轮对的镟修工作主要分为以下两个步骤:一是需要确定轮缘厚的恢复阈值和轮径的切削量,即镟床要按照镟修后的车轮轮缘厚值进行镟修加工,相应对轮径进行切削以降低踏面测量的基准点;第二,在轮对的轮缘轮径参数确定之后,还需要保证镟修后的轮对能够保持一个平滑的合理的外形轮廓,使得列车在正常运行过程中,满足车辆的一系列动力学性能。本文主要对第二个步骤进行重点研究。
本文围绕城轨车轮镟修后的踏面外形轮廓展开研究,提出了基于Kriging[14-15]代理模型的单目标优化方案和多目标优化方案,对改进之后的结果与标准踏面的性能进行对比,研究动力学性能的各项指标,并比较两种模型的优劣。结果表明多目标优化相比单目标而言可以同时对多个相互影响和制约的目标进行优化,在多个优化目标之间寻找一个折中点,使系统的综合性能得到提高。
1 城轨车轮踏面外形Kriging代理模型变量
Kriging代理模型是在分析设计变量在空间上的相关性的基础上,根据已知样本信息来构建输入变量与输出变量之间的映射关系,从而预测某一未知待测点的信息的。
Kriging模型是对线性回归分析的一种改进,Kriging模型需要利用在某一点为中心的邻域内的已知设计点的信息对待测样本点进行预测,即利用线性加权法将该点的邻域内样本设计点的信息加权来估计该点未知信息。利用获得信息的最小误差方差来确定加权的权系数。因此,Kriging模型本质上是最优的线性无偏估计。
Kriging模型的组成:多项式和随机分布
y(x)=fT(x)β+Z(x)
(1)
式中,fT(x)=[f1(x1),f2(x2),…,fq(xm)]T为已知的多项式回归模型;β=[β1,β2,…,βq]T为相对应的待估参数;Z(x)为一随机过程,具有如下统计特征
(2)
式中,xi和xj是训练样本中的两个点;R(θ,xi,xj)是相关性系数,包含待定参数θ,用于表示两个样本点之间的空间相关性。因此,Kriging代理模型将任意的响应值都视为一个服从正态分布随机变量,如此模型具有更好的灵活性,而不限定于某种特定的形式。
2009年10月至12月,广州地铁进行了较为集中的镟轮作业,先后实测结果如表1所示。可以看出,城轨车轮在经过镟修之后再次上线后,车轮的磨耗以及钢轨的磨耗会加剧。轮对镟修会破坏已经进入稳定磨损状态的轮轨接触关系,轮轨将会重新回到运行初期的磨合阶段,磨耗量平均值增大。因此镟修作业后车轮保持一个具备良好的轮轨接触关系的外形十分重要。现有的车轮型面的优化,主要是对踏面外形的优化,本文在TBT449—2003标准中已经给出的几种LM磨耗型踏面外形的基础上基于车辆动力学性能做相应的型面优化。
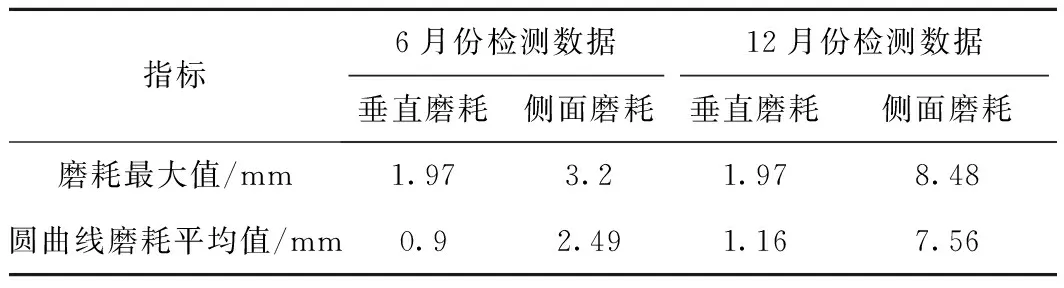
表1 2009年广州地铁5号线磨耗状况对比
选取我国广泛应用的LM磨耗型踏面进行分析。其几何特性如图1所示。根据TBT449—2003分析,LM踏面外形能够依据轮缘厚的尺寸不同分为4种,分别为26,28,30,32 mm[16],综合4种磨耗型踏面的几何特性,有几个不变的参数可以进行确定。我们可以分析得到需要采用5个参数能够描述这段圆弧r1,r2,r3,xR3,xR4,从左向右4段圆弧依次为圆OR1,OR2,OR3,OR4,A点为轮缘厚测量点,对于确定了轮缘厚值的预镟轮对,A点和E点值为固定值A(-39.8,-12),E(42.3,2.52)。
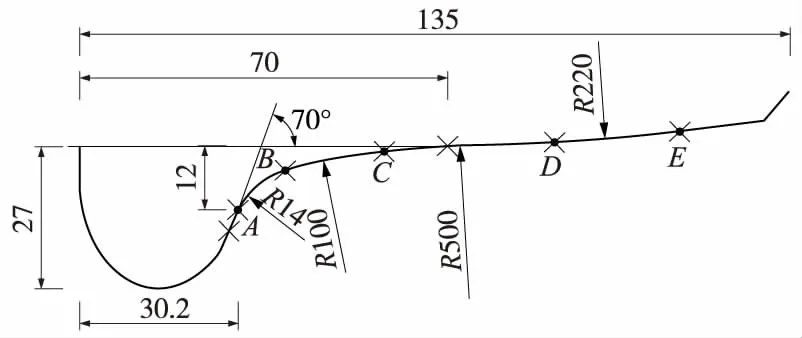
图1 LM磨耗型踏面几何特性(单位:mm)
由已知的A点坐标可得到两个方程
(3)
可得圆OR1的圆心坐标O1(xR1,yR2)。
由于圆OR3必经过踏面基准点,则现已知圆OR3的圆心横坐标xR3以及半径r3,则可得出O3的纵坐标yR3。
已知E点坐标,根据圆OR4的特点及圆OR3和圆OR4外切的特性,可得以下两个方程
(4)
可以算出yR4和r4。
(5)
可得出圆OR2的圆心坐标O2(xR2,yR2)。
至此,4段圆弧均可唯一确定。表1即为使用的设计变量及其范围的依据。

表2 标准试验系统结果数据设计变量
2 单目标车轮踏面Kriging优化方案
2.1 目标函数
磨耗性能是用于表征车辆的曲线通过性能,采用英国首创的磨耗指数来表示
WZ=Fxξx+Fyξy
(6)
式中,WZ为列车轮对的磨耗指数;Fx,Fy分别为轨道对轮对的左右轨的纵向和横向蠕滑力;ξx,ξy分别为轮对的左右轮与铁轨的纵向和横向蠕滑率。
目标函数f(x)与轮轨间损耗有关,为
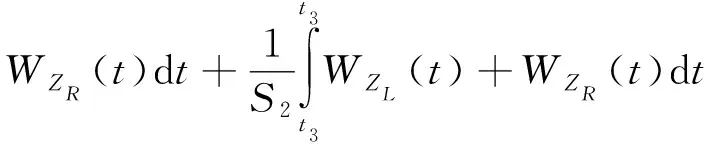
(7)
WZL(t)=FxL(t)ξxL(t)+FyL(t)ξyL(t)
WZR(t)=FxR(t)ξxR(t)+FyR(t)ξyR(t)
(8)
式中:WZL(t),WZR(t)分别为某时间点列车导向轮对双轮的磨耗指数;FxL(t),FyL(t),FxR(t),FyR(t)分别为某时刻导向轮对的左右轨的纵向和横向蠕滑力;ξxL(t),ξyL(t),ξxR(t),ξyR(t)分别为某时刻导向轮对的左右轮与轨道的纵向和横向蠕滑率;S1,S2,S3分别为[t0,t1],[t1,t2],[t2,t3]时间段内车辆运行的距离。
2.2 约束条件
为避免发生事故,减轻轮轨损耗,约束条件采用脱轨系数,轮重减载率,平稳性指标。
(1)约束函数g1(x)与脱轨系数相关,则
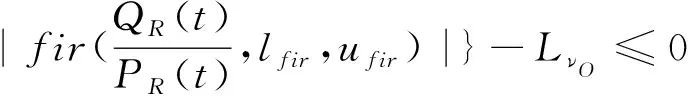
(9)
式中,Lv0为车轮的脱轨系数的最大上限值,根据TB/T2360-93取0.8;PL(t),PR(t)分别为某时刻铁轨作用于导向轮对的垂向力;fir(·,lfir,ufir)为带通滤波器;lfir,ufir分别为带通滤波器的截断低频率和截断高频率。
(2)约束函数g2(x)和轮重减载率相关,则
(10)
式中,ΔP为轮重减载量;P为平均轮轨垂向力;P0=0.6;P0为轮重减载率安全允许限值。
(3)目标函数g3(x)与平稳性相关,则
g3(x)=SPl-SPl0≤0
(11)
按照《客运专线铁路工程竣工验收动态检测指导意见》规定,SPl0=2.5。
2.3 模型精度检验
依次对其他指标进行精度判定,并采用均方根误差值进行误差计算,该评价指标的最大值为0.2。由表3可以看出,各指标的误差值均在合格范围内,因而此模型可以进行仿真并对其进行计算。

表3 单目标优化均方根误差
2.4 Kriging优化模型的求解过程
模型求解过程见图2,具体步骤如下。
(1)给定待优化的初始踏面形状,车体动力学模型,确定样本点的初始空间E0,中心点x0,步长δ0。
(2)在初始空间进行最优拉丁超立方试验设计,进而得到样本点。
(3)利用Kriging插值法对目标函数及约束条件进行插值,建立车轮踏面优化模型。回归部分采用一阶多项式模型。随机过程采用GAUSS函数。进行模型精度检验。
(4)求解优化问题
(12)
利用惩罚因子将优化问题转化成只带边界约束条件的优化问题,将约束条件通过罚因子表示出来,即
(13)
Ωg={i|gi(x,θ)>0,j=1,2,…,N}
(14)
则可得子优化问题
(15)
再利用遗传算法即可得到优化问题的最优解x(k+1)*以及所对应的代理模型的目标值。
(5)判断最优解的信息符合收敛准则与否。当第一次迭代时,直接执行步骤6。当迭代两次之后时,计算优化过程中第k次与第k-1次所求的可能最优解所对应的模型响应值的相对差值,判断该值符合收敛标准与否。若收敛,过程结束,则第4个步骤获得的最优解就是真实模型的最优解;若不收敛,即进入第6个步骤。
(6)采用信赖域更新方法。可以根据下式来确定信赖域的更新半径δ(k+1)
(16)
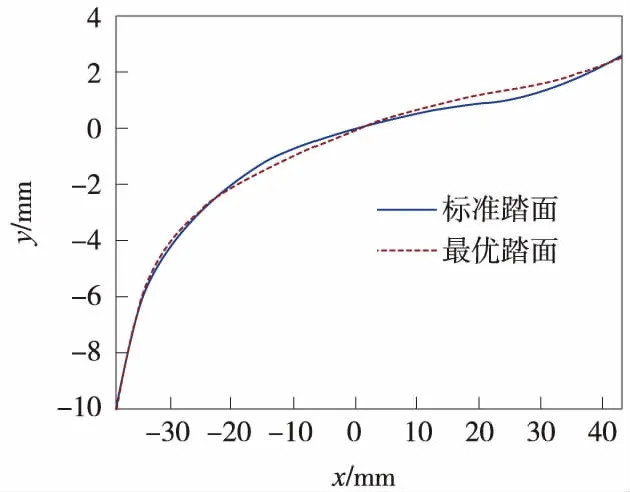
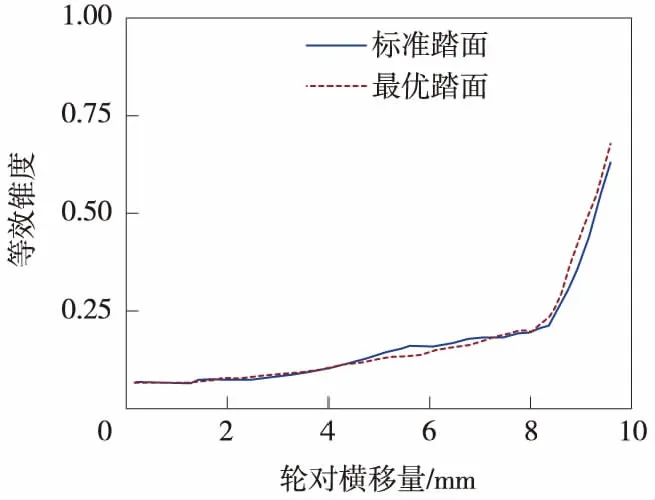
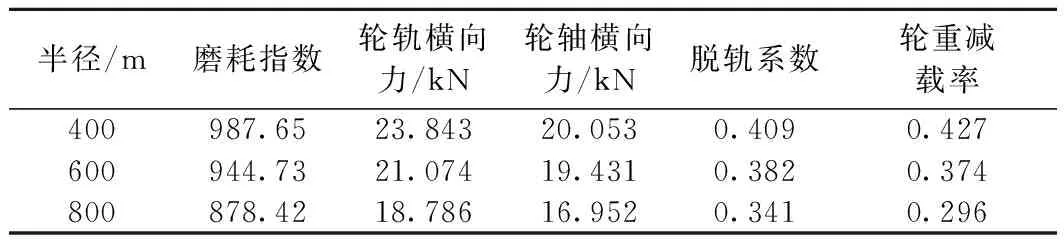
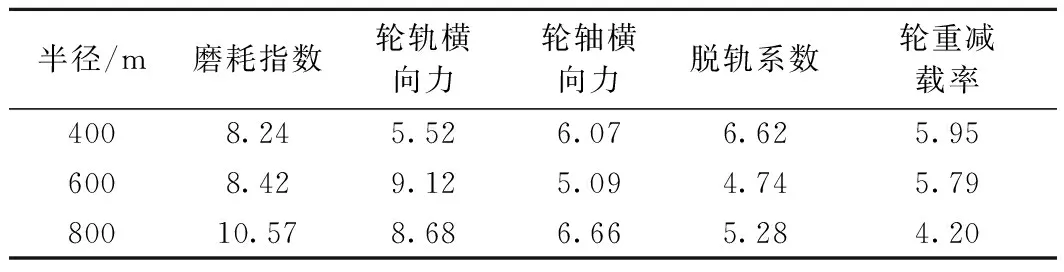
式中,m1,m2,S1,S2为系数,其中0 第k+1次迭代的子空间Ek+1由式确定 n=1,2,…,N} 图2 单目标优化Kriging模型求解流程 与磨耗指数相关的目标函数f1(x)见2.1节。 与脱轨系数相关的目标函数 (17) 式中,QL(t),QR(t)分别为钢轨受到车轮作用产生的横向力;PL(t),PR(t)分别为左右车轮的垂向力;fir(·,lfir,ufir)为带通滤波器,lfir,ufir分别为带通滤波器的截断低频率和截断高频率。 与平稳性指标相关的目标函数 f3(x)=SPl (18) 与轮轨横向力有关的约束函数 g1(x)=max{|fir(QL(t),lfir,ufir)|, |QR(t),lfir,ufir|}-Q0≤0 (19) 与轮轴横向力相关的约束函数 g2(x)=max{|fir(HL(t),lfir,ufir)|, |HR(t),lfir,ufir|}-H0≤0 (20) 采用均方根误差值进行误差计算,结果如表4所示。由表4可以看出,各指标的误差值均在合格范围内,因而可以对该模型进行仿真。 表4 多目标优化均方根误差 以磨耗指数、脱轨系数和平稳性为目标函数的多目标Kriging优化问题 (21) 基于多目标的Kriging优化模型的求解,与单目标的区别之处在于目标函数的不同。运用遗传算法对其进行求解时,对目标函数采用线性加权和法,由于3个目标函数并无明显的主次关系,因此权重根据函数值本身不同的数量级确定。再引入惩罚因子,则式(18)转变为 (22) 再利用遗传算法对式(15)求解即可得到优化问题的最优解x(k+1)*以及所对应的代理模型的目标值,求出的最优解根据信赖域更新方法判断符合收敛准则与否[17]。 初始踏面采用TBT449—2003中所规定的轮缘厚为30 mm的磨耗型车轮踏面,初始样本中心点为x0=[14,100,500,32,15],δ0=[1.5,10,20,4,2]。进行优化设计。 在第5次迭代时,目标函数的变化值小于给定的阀值,优化过程结束。求出的最优踏面与标准踏面的对比如图3所示。图4是两种踏面的等效锥度的对比。 图3 单目标优化标准踏面和最优踏面的比较 图4 单目标优化标准踏面和最优踏面等效锥度比较 由图4可以看出,优化后的等效锥度要显著大于标准踏面。在偏移量6 mm时,优化的踏面的等效锥度数值为0.208 5,而同样的LM标准踏面的等效锥度为0.171 9。当横移量呈现轮缘贴靠的时候,等效锥度迅速变大。 分析曲线通过性能,根据相关规定设置了3种理想曲线通过轨道,半径分别为400、600、800 m。以条形图的形式比较不同条件下最优踏面通过不同半径弯道曲线的动力学各指标的变化情况[18],如图5所示。 图5 单目标优化标准踏面和最优踏面曲线通过能力比较 由图5(a)可以看出,采用最优踏面的列车在通过曲线轨道时,目标函数磨耗指数有较大幅度的降低,经过计算发现列车在通过3种不同曲线半径轨道时的磨耗指数降幅分别为13.3%、15.2%和16.6%,曲线半径越小,降幅越大。但对于其他的指标并不一定有着相同的趋势。 脱轨系数在半径400 m和600 m的轨道上分别恶化8.9%与6.7%,当曲线半径增大到800 m时,最优踏面的脱轨指标发生优化,幅度较小,为3.6%。轮轨横向力指标在半径400 m和800 m的轨道上,最优踏面进行了较小幅度的优化,优化率仅为2.75%和1.5%。半径为600 m时,轮轨横向力甚至恶化1.6%。轮重减载率在3个不同曲线轨道上均发生了一定的恶化,分别为6.2%、5%和0.64%。轮轴横向力同样发生微弱的优化与恶化。 由以上分析可以得出,以磨耗指数单个目标函数做优化,对磨耗指数本身有着较好的优化效果,但对于其他指标来说,优化效果不明显,甚至可能会变差。同时,会造成直线运行能力的恶化。 初始踏面采用TBT449—2003中所规定的轮缘厚为30 mm的磨耗型车轮踏面进行多目标优化设计。Kriging优化模型的初始样本中心点为x0=[14,100,500,32,15],δ0=[1.5,10,20,4,2]。利用该优化模型求出的最优踏面与初始踏面的对比如图6所示。其等效锥度的对比如图7所示。 图6 多目标优化标准踏面和最优踏面的比较 图7 多目标优化标准踏面和最优踏面等效锥度比较 由图7可以看出,横移量在0~4 mm,优化后的踏面的等效锥度与标准踏面基本持平,横移量在4~7 mm,等效锥度略小于标准踏面,横移量大于7 mm后,优化踏面的等效锥度略大于标准踏面。 同样设置了3种半径分别为400、600、800 m的理想曲线通过轨道。车辆以适当的速度通过带有轨道激励的曲线轨道。表5为最优踏面通过不同半径的曲线轨道的性能指标值。同时,将优化后的指标值与标准踏面进行对比,计算得到该优化模型的优化率,如表6所示。 表5 装载最优踏面的列车曲线通过能力指标 表6 装载最优踏面的列车曲线通过能力的优化率 % 由表6可以看出,在半径为400 m的曲线轨道上装载优化后的踏面的列车的磨耗指数优化率为8.24%,较单目标模型在相同条件下的13.3%的优化率要较小一些。另外两种大半径的轨道上磨耗指数的优化率同样比其要小。但是约束条件都有不同程度的优化,并未发生某些性能变差的情况。半径为400 m的曲线轨道上,轮轨横向力的优化率为5.52%,轮轴横向力的优化率为6.07%,脱轨系数的优化率为6.62%,轮重减载率的优化率为5.95%。半径为600 m的曲线轨道上,磨耗指数的优化率与400 m轨道相比略微增大为8.42%,轮轨横向力的优化率为9.12%,轮轴横向力的优化率为5.09%,脱轨系数的优化率为4.74%,轮重减载率的优化率为5.79%。半径为800 m的较大半径曲线轨道上,磨耗指数的优化率与400 m轨道相比提高幅度较大,为10.57%,轮轨横向力的优化率为8.68%,轮轴横向力的优化率为6.66%,脱轨系数的优化率为5.28%,轮重减载率的优化率为4.2%。总的来说,列车的曲线通过能力在3种曲线轨道上都得到明显改善。这与等效锥度的走势大致相同,在横移量较大时,等效锥度较高有利于曲线通过。 由如上分析可得,采用线性加权和与信赖域相结合的方法对建立的Kriging优化模型进行优化,最优解只需要信赖域变更5次即可获得,虽然磨耗指数的优化率没有之前单目标的优化率高,但没有某个指标出现恶化情况,导致曲线通过能力不平衡。由此说明所采用的多目标优化模型,在平衡不同性能指标方面有着较好的优化效果。相比建立的单目标优化模型,多目标优化具有较好的均衡性。 本文围绕城轨车轮镟修后的踏面外形轮廓展开研究,提出了基于Kriging代理模型的单目标优化方案和多目标优化方案,以磨耗指数、平稳性和脱轨系数多个指标为目标函数建立Kriging多目标优化模型,采用线性加权和与信赖域更新相结合的优化算法求解,从优化结果可以看出,装载优化踏面的列车的直线平稳性与曲线通过能力都可以得到一定程度的提高。多目标优化与单目标相比很大的优势就是均衡性比较好,同时优化多个相互影响的目标,使系统的各方面综合性能得到提高,从而在多个优化目标之间寻找一个折中点,使系统的综合性能得到提高。 [1] 王永亮,张星臣,徐彬,等.城市轨道交通网络化列车开行方案优化方法[J].中国铁道科学,2012(5):120-126. [2] 刘灿龙.地铁轮轨磨耗的初步研究[J].城市轨道交通研究,2008(10):57-59. [3] 陆缙华.广州地铁1号线车辆的磨损情况分析[J].电力机车技术,2001(3):16-17. [4] 邓军.广州地铁车辆轮对损伤行驶及原因浅析[J].机车电传动,2008(1):71-74. [5] 李海东.基于CRH2的车轮磨耗和经济型镟修踏面的研究[D].南昌:华东交通大学,2014. [6] 李煜.车轮磨耗对车体动力学性能影响研究[D].大连:大连交通大学,2014. [7] 常崇义,王成国,金鹰.基于三维动态有限元模型的轮轨磨耗数值分析[J].中国铁道科学,2008(4):89-95. [8] Braghin F, Lewis R, et al. A mathematical model to predict railway wheel profile due to wear[J]. Wear, 2006,261(2):1253-1264. [9] 员华,肖胜强,汪洋.基于磨耗量统计的轮对等级镟修可行性研究[J].城市轨道交通,2006(1):43-45. [10] Pascual F,Marcos J A.A common playground for design and maintenance engineering in the Taglo engineering cycle[C]. Proceeding of the Joint Rail Conference, 2004:193-199. [11] 许宏,员华,王凌,等.基于高斯过程的地铁车辆轮对磨耗建模及其镟修策略优化[J].机械工程学报,2010(7):88-95. [12] 王珍.动车组整车轮对镟修优化决策模型的研究[D].成都:西南交通大学,2013. [13] Jendel T. Prediction of wheel profile wear-comparisons with field measurements[J]. Wear, 2002,253(4):89-95. [14] 谢锋.基于近似模型的车架不确定性多目标优化[D].长沙:湖南大学,2013. [15] Lophaven S N,Nielsen H B,Sondergaard J.DACE-A Matlab Kriging Toolbox,Version2.0[Z]. Technical Report,2002. [16] 朱士友,潘丽莎,员华.轮对等级镟修对车辆平稳性的影响分析[J].城市轨道交通研究,2016(7):46-48. [17] 陈国栋.基于代理模型的多目标优化方法及其在车身设计中的应用[D].长沙:湖南大学,2012. [18] 国家标准局.GB5599—85 铁道车辆动力学性能评定和试验鉴定规范[S].北京:中国标准出版社,1986.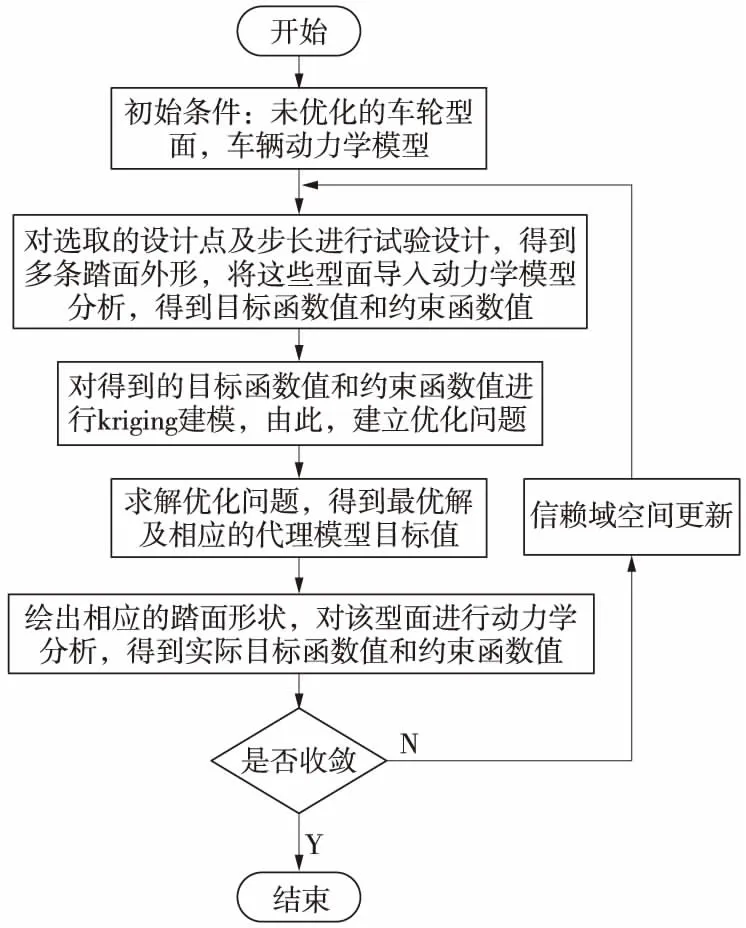
3 多目标车轮踏面Kriging优化方案
3.1 目标函数
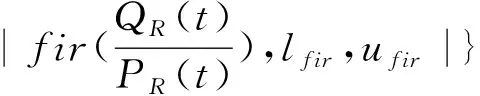
3.2 约束条件
3.3 模型精度检验

3.4 优化模型的求解
4 仿真结果分析
4.1 单目标优化仿真结果

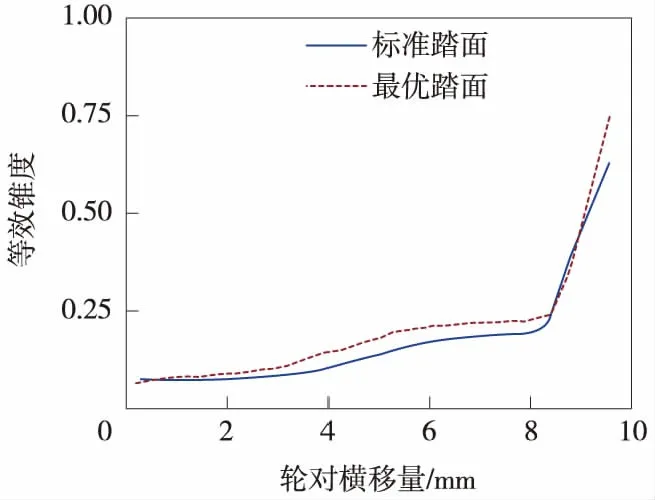
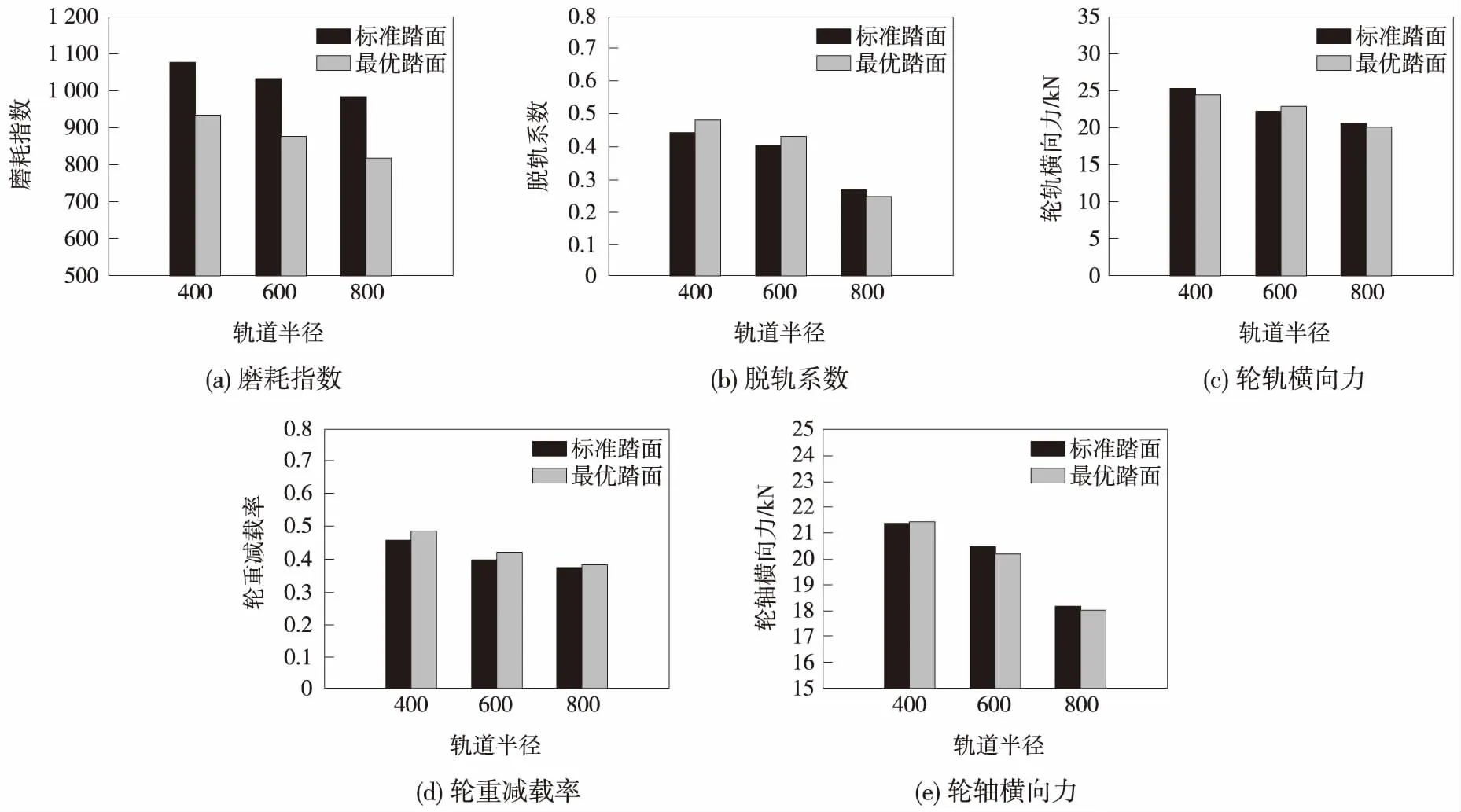
4.2 多目标优化仿真结果
5 结论
