KNN-朴素贝叶斯算法的滚动轴承故障诊断

， ，

(1.四川大学 电子信息学院，成都 610065;2.电子信息控制重点实验室，成都 610036)

0 引言

滚动轴承是旋转机械中较为常见的零部件，滚动轴承故障往往会导致其他零部件发生故障，进而影响设备的正常运行。滚动轴承在使用过程中一般会经历正常运转、故障、失效几个阶段。若检测到滚动轴承发生故障，及时停机更换部件，以防轴承失效，造成更加严重的后果，同时可以有效地降低设备故障带来经济损失。因此，对滚动轴承的故障诊断有着重要的研究意义[1]。

对于旋转设施关键的滚动轴承故障诊断，获取故障信息的方法有温度检测法，振动监测法以及光纤检测法等[1]。目前一般采用振动监测法对滚动轴承故障诊断。传统的诊断技术一般是针对滚动轴承振动信号的时频域特征来提取特征向量进行故障识别。常用的识别算法有支持向量机(SVM)、人工神经网络(ANN)、决策树、随机森林等。使用支持向量机进行故障诊断获取的诊断结果置信度偏低；人工神经网络对训练样本要求较高，容易陷入局部极小值，并且运算速度慢。使用小波变化与小波分析对滚动轴承信号处理可以将信号的低频特征与高频特征很好的表征出来，小波包分析是在小波分析的基础上对信号更进一步的分析与重构。滚动轴承振动信号的时频信号经小波包能量法提取特征后，各子频带能量分布存在较大差异，相较于时频域特征更适合做故障识别。小波变换由于其能够对不同频域的信号进行特征分析，抗干扰能力强，并且对输入信号要求不高，成为近些年研究的热点[2-9]。目前，越来越多的研究将小波包能量法与机器学习相结合，实现滚动轴承的故障诊断。文献[10]中提出使用小波包能量法与BP神经网络算法相结合，对滚动轴承故障诊断，该方法在神经网络设计合理的情况下，效果较好，但算法容易陷入局部极值。文献[11]提出C4.5决策树与小波包能量法相结合，总体正确率达到92%。传统分类算法KNN算法与朴素贝叶斯算法在模式识别中的到广泛应用[12-15]。KNN算法与朴素贝叶斯算法在滚动轴承故障诊断中单独使用分类效果比较一般，无法达到工业要求。

本文提出一种KNN算法与朴素贝叶斯算法结合的改进算法，可以有效的提高滚动轴承故障诊断的识别率。首先使用K值为1、3、5、7的KNN算法对滚动轴承振动信号特征数据进行分类，得到初步分类结果集，将结果集作为朴素贝叶斯算法的输入，再使用朴素贝叶斯算法进行分类，得到最终分类结果。经实验验证表明，改进后算法的准确率得到了有效提高。

1 小波包的滚动轴承故障特征向量提取

小波包变换是在多分辨率分析基础上构成的一种更为精细的正交分解方法 ,它在全频带内对信号进行多层次的频带划分 ,不仅继承了小波变换所具有的良好时频局域化优点 , 而且继续对没再分解的高频频带进一步分解 ,并能够根据被分析信号的特征 ,自适应地选择相应频带 , 使之与信号频谱相匹配 ,从而提高了时频分辨率 ,因此小波包在信号特征提取方面具有更广泛的应用价值[ 16]。

1.1 小波包定义

给定正交尺度函数φ(t)与小波函数φ(t)，其尺度关系为

(1)

(2)

其中:式(1)、(2)中h0k、h1k为多分辨率分析中的滤波器系数。

进一步推广至二尺度方程，可以得到如下递推关系

(3)

(4)

当n=0时，ω0(t)=φ(t)，ω1(t)=φ(t)，以上定义的函数集合{ωn(t)}n∈Z为由ω0(t)=φ(t)确定的小波包。

小波包分解：

(5)

小波包重构：

(6)

1.2 小波包能量提取特征

滚动轴承的振动信号共分为正常信号、外圈故障信号、内圈故障信号、滚动体故障信号4种状态信号。对滚动轴承的时域振动信号采用db5作为小波包函数对振动信号进行三层小波包分解，这样可以得到第3层上8个频带的小波包分解系数，然后对第3层上每个节点进行小波包重构，对重构信号进行能量统计分析，对第3层上各个子频带上的能量值做归一化处理，得到8个归一化的频带能量特征，作为组合算法的输入。

2 KNN-朴素贝叶斯组合算法及流程

K近邻(k nearest neighbor，KNN)算法是解决分类问题中最为常用的算法之一，其算法具有原理简单易于理解、实现方便、分类有效等特点。KNN分类算法的主要思想是：先计算待分类样本与已知类别的训练样本之间的距离，找到距离与待分类样本数据最近的K个样本；再根据这些样本所属的类别来判断待分类样本数据的类别。由于同时使用多个参数K值不同的KNN算法对同一特征数据集分类得到的结果是相互独立的，符合朴素贝叶斯算法中假设所有属性相互独立的假设，使用朴素贝叶斯算法可以进一步提高KNN分类器性能。朴素贝叶斯分类的原理是求解向量D(d1,d2,...,dm)属于类别C(C1,C2,...,Cn)的概率值(P1,P2,...,Pn)，其中Pn是指向量D(d1,d2,...,dm)属于类别Cn的概率，max(P1,P2,...,Pn)为向量D对应的类别。组合算法构造算法步骤如下。

Step 1：设X(x1,x2,...,xm)作为小波包能量法提取的滚动轴承振动信号特征向量集合。

Step 2：将X分为训练集Xtrain与测试集Xtest两部分。

Step 3：设置参数K值：K值的一般选择1～10，本文K值选取1、3、5、7，选择的K值为奇数，尽量避免了投票过程中可能产生不同类别的最邻近数目相同的情况。

Step 4：计算训练集样本数据和测试集样本数据的距离。

Step 5：为测试集样本数据选择K个与其距离最小的样本。

Step 6：得到测试集分类结果。对每个测试样本统计出最临近K个样本中大多数样本所属的分类，使用投票法，确定待分类数据的类别，得到4个参数K值不同的KNN算法的初步分类结果集D(d1,d2,...,dm)。

Step 7：得到C(C1,C2,...,Cn)，对每个特征属性计算所有划分的条件概率(P1,P2,...,Pn)。

Step 8：对于一条待分类数据如果Pi=max(P1,P2,...,Pn)，那么该数据的类别为i。以此训练分类器，得到贝叶斯分类模型。

Step 9：使用训练模型对测试数据集分类，得到最终分类结果。

3 故障诊断实验

3.1 实验数据

本文实验数据使用美国 Case Western Reserve University 电气工程实验室轴承中心实验台所采集的数据。滚动轴承实验平台如图1所示，实验平台包括左侧一个2马力的电机(1 hp=746 W)，中间一个转矩传感器，右侧一个功率计和电子控制设备。

图1 凯斯西储大学轴承故障实验台

实验时，采用数据为电机故障直径为0.007英寸，转速为1 750 rmp，采样频率为12 kHz部分数据，其中外圈故障信号取采集点为6点钟方向作为实验数据。原始实验数据包含滚动轴承的4种运行状态，分别是正常状态、内圈故障状态、滚动体故障状态、外圈故障状态。如下图2所示为采集的滚动轴承时域振动信号处于正常状态及发生不同故障时的时域振动信号波形。

图2 轴承各个状态下时域振动信号

通过观察图2，滚动轴承的时域振动波形区分度较低，很难区分出正常信号与故障信号，为了获取区分度更好的特征，对滚动轴承实现有效的故障诊断，对4种运行状态下的滚动轴承振动信号进行小波包能量特征提取。对滚动轴承4种不同状态下的能量特征数据各取80组，一共320(4*80)组实验数据。每组数据时域振动信号包含1 024个点，对时域振动信号数据进行小波包能量特征提取，首先使用db5作为小波包函数对振动信号进行三层小波包分解，并在每个节点上进行小波包重构，对重构信号进行能量统计分析，得到一个8维小波包能量频带特征向量，然后将获取的特征向量进行归一化处理。滚动轴承正常状态以及不同故障状态下的能量分布情况如图3所示 。

图3 轴承各个状态下能量谱

通过图3我们可以比较直观的观察到滚动轴承处于不同状态时，其振动信号各子频带的能量分布存在的差异较大，比较易于识别。轴承处于正常状态时，能量主要集中分布在前2个子频带，其中前两个子频带之和所占比重超过了总能量的80%，与其他故障状态下能量分布有很大不同，易于区分。内圈故障、滚动体故障和外圈故障3种状态的能量主要分布在子频带3和子频带7上，其余频带所占能量比重相对较少，但3种不同状态下能量谱分布还是有所不同。对比滚动体故障信号能量谱与外圈故障信号能量谱，滚动体故障信号能量谱子频带3能量所占比重小于子频带7，而外圈故障与之相反。相比这两种故障能量谱能量分布，内圈故障信号能量谱分布相对分散，子频带3和子频带7的能量和平均只占总能量的65%左右。

3.2 实验方案及分析

对上述滚动轴承4种状态下4*80(320)组数据中每种状态下各取60组数据作为训练数据集，其余20组作为测试数据集验证组合算法性能。实验中分别使用参数K值取1、3、5、7的KNN算法以及朴素贝叶斯算法与组合算法做比较。

对于KNN算法使用训练集作为样本数据集，直接对测试数据集进行预测，得到分类结果。实验结果如表1所示。

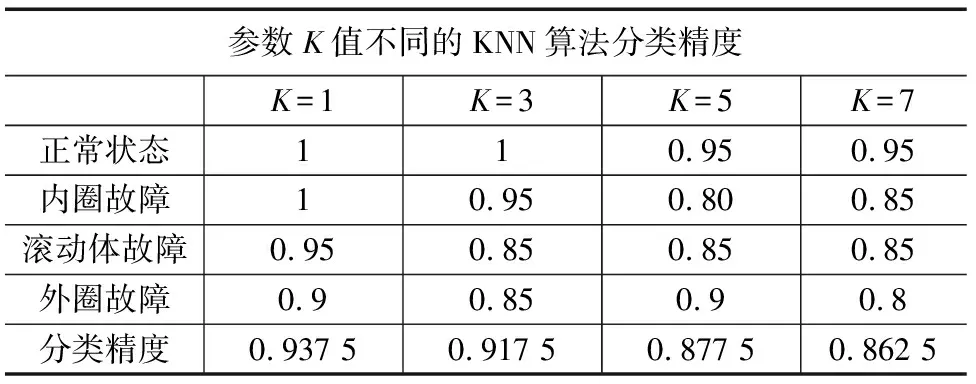
表1 KNN算法分类结果比较

从表1中可以看出使用测试数据集使用K值不同的KNN算法分类效果也不同，从分类结果中可以看出当K值为1时KNN算法对滚动轴承的故障类型分类效果最好，但其他KNN算法在某种故障类别上个诊断率同样可以达到较好的诊断效果，例如参数K为5的KNN算法在外圈故障诊断中表现出较好的精度。当使用参数K=1的KNN分类器时分类性能最好，能达到93.75%的正确率。

使用朴素贝叶斯算法与组合算法对滚动轴承进行故障诊断，同样取滚动轴承4种状态下4*80(320)组数据中4*60组数据(每种状态下各取60组)作为训练数据集，剩余数据(每种状态各20组)作为测试数据集。得到分类结果如下表2。

表2 分类结果比较

由上表2中可以看出组合算法的分类精度较K=1的KNN算法提高了5%，比朴素贝叶斯算法精度提高了11.25%，由此可见组合算法的分类效果相较于传统KNN算法及朴素贝叶斯算法有所提高，且算法精度达到98.75%,能够有效的识别滚动轴承的故障状态，达到工业要求水准，可以在实际生产中应用推广。

4 结语

提出了一种KNN-朴素贝叶斯组合算法用于提高滚动轴承的故障识别率，实现滚动轴承故的有效识别。单一使用传统KNN算法或朴素贝叶斯算法在滚动轴承的故障识别中分类效果不佳，不能有效的识别滚动轴承的故障状态，达到工业应用标准。针对时域特征不明显的滚动轴承振动信号使用小波包能量法提取特征，可以得到差异较大的一组特征量，使用多个参数K值不同的KNN算法对数据进行初步分类，得到一个初步分类结果集，再使用朴素贝叶斯算法对初步分类结果集进行优化再分类，可有效的提高分类精度，实现滚动轴承故障的有效诊断，在实际应用中有较好的推广意义。

参考文献:

[1]王泽文. 基于振动信号的滚动轴承故障诊断与预测系统研究[D]. 中国矿业大学, 2014.

[2]Kankar P K, Sharma S C, Harsha S P. Fault diagnosis of ball bearings using continuous wavelet transform [J]. Applied Soft Computing, 2011, 11(2):2300-2312.

[3]Muruganatham B, Sanjith M A, Krishnakumar B, et al. Roller element bearing fault diagnosis using singular spectrum analysis [J]. Mechanical Systems and Signal Processing, 2013, 35(1/2):150-166.

[4]Hao R, Chu F. Morphological undecimated wavelet decomposition for fault diagnostics of rolling element bearings [J]. Journal of Sound and Vibration, 2009, 320(4/5):1164-1177.

[5]Cheng J, Yu D, Yang Y. Application of all impulse response wavelet to fault diagnosis of rolling bearings [J]. Mechanical Systems and Signal Processing, 2007, 21(2):920-929.

[6]Tang B, Liu W, Song T. Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution [J]. Renewable Energy, 2010, 35(12): 2862-2866.

[7]左 来. 基于小波包分析和LS-SVM的柴油机故障诊断方法[J]. 计算机测量与控制, 2009, 17(11):2150-2152.

[8]蔡艳平, 李艾华, 石林锁, 等. 基于EMD 与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击, 2011, 30(2):167-172.

[9]胥永刚, 孟志鹏, 陆 明,等. 基于双树复小波包和 AR 谱的滚动轴承复合故障诊断方法[J]. 北京工业大学学报, 2014, 40(3): 335-340.

[10]张 军, 陆森林, 和卫星,等. 基于小波包能量法的滚动轴承故障诊断[J]. 农业机械学报, 2007, 38(10):178-181.

[11]赵庆恩, 黄宏伟, 冯 坤,等. 基于小波包能量-决策树的滚动轴承混合故障诊断[J]. 轴承, 2016(06):43-46.

[12]Chelly Z，Elouedi Z.Hybridization schemes of the fuzzy dendritic cell immune binary classifier based on different fuzzy clustering techniques[J]．New Generation Computing，2015，33(1)：1-31．

[13]Khedr A, Gulak G, Vaikuntanathan V.scalable homomorphic implementation of encrypted data·classifiers[J]．IEEE Transactions on Computers，2016，65(9)：2848—2858．

[14]Fredman J S，Calvet L E,Bessiere P．Bayesian inference with Muller C-elements[J]．IEEE Transactions on Circuits and Systems I-Regular Papers，2016，63(6)：895-903．

[15]张金萍, 白广彬. 基于主元分析与KNN算法的旋转机械故障识别方法[J]. 机械设计与制造, 2017(6):23-25.

[16]程正兴.小波分析算法与应用[ M] .西安:西安交通大学出版社, 1998.